Probability Questions and Answers

Math
ProbabilityThe standard deviation of the weights of elephants is known to be approximately 15 pounds. We wish to construct a 95% confidence interval for the mean weight of newborn elephant calves. Fifty newborn elephants are weighed. The sample mean is 244 pounds. The sample standard deviation is 11 pounds. In words, define the random variables X and x̄.
x is the weight in pounds of a newborn elephant, and x̄ is the sample mean of the 50 baby elephants.
x is the weight in pounds of a newborn elephant, and x̄ is the standard deviation of the weights of baby elephants.
x is the sample mean of the weights of the sample of 50 newborn elephant, and is the sample standard deviation of weights of the sample of 50 baby elephants.
x is the weight in pounds of a newborn elephant, and x̄is the average of weights of the sample of 50 baby elephants.
x is the average of weights of the sample of 50 newborn elephant, and x̄ is the weight in pounds of a baby elephant.
Math
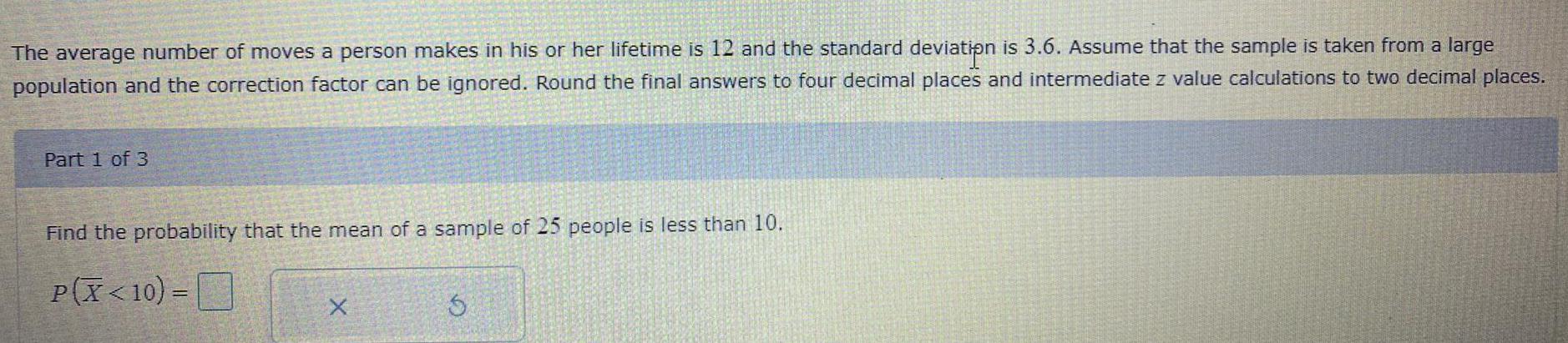
ProbabilityThe average number of moves a person makes in his or her lifetime is 12 and the standard deviation is 3.6. Assume that the sample is taken from a large population and the correction factor can be ignored. Round the final answers to four decimal places and intermediate z value calculations to two decimal places.
Part 1 of 3
Find the probability that the mean of a sample of 25 people is less than 10.
P(X<10)=

Math
ProbabilityIn a game of dice, each player throws two
dice and finds their sum. If the sum is not a
prime number, then it is added to the player's
score. If the sum of the dice is a prime
number, no points are awarded and the
player's turn is over.
Find the probability that a player rolls a sum
that is a prime number. Enter your answer as
a decimal rounded to three significant
figures.

Math
ProbabilityA poll is given, showing 45% are in favor of a new building project. If 4 people are chosen at random, what is the probability that exactly 1 of them favor the new building project?
Math
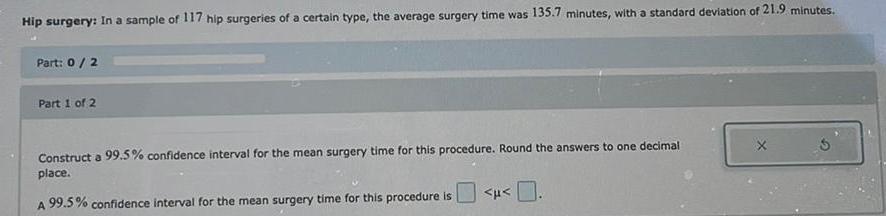
ProbabilityHip surgery: In a sample of 117 hip surgeries of a certain type, the average surgery time was 135.7 minutes, with a standard deviation of 21.9 minutes.
Part: 0 / 2
Part 1 of 2
Construct a 99.5% confidence interval for the mean surgery time for this procedure. Round the answers to one decimal
place.
A
99.5% confidence interval for the mean surgery time for this procedure is
<p<
3
Math
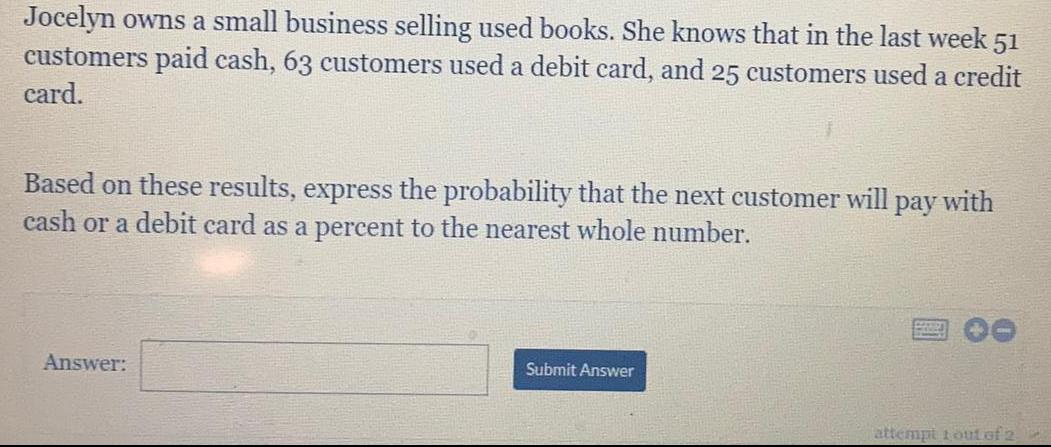
ProbabilityJocelyn owns a small business selling used books. She knows that in the last week 51 customers paid cash, 63 customers used a debit card, and 25 customers used a credit card.
Based on these results, express the probability that the next customer will pay with cash or a debit card as a percent to the nearest whole number.

Math
ProbabilityA city council consists of six Democrats and eight Republicans. If a committee of five people is selected, find the probability of selecting two Democrats and three
Republicans.
7
(Type a fraction. Simplify your answer.)
*****
![9. [0/1 Points]
PREVIOUS ANSWERS WAS WANEFMAC7 7.3.021.MI.
While selecting candy for students in his class, Professor Murphy must choose between gummy candy and licorice nibs. Gummy candy packets come in five sizes, while packets of licorice nibs come
in two. If he chooses gummy candy, he must select gummy bears, gummy worms, or gummy dinos. If he chooses licorice nibs, he must choose between red and black. How many choices does he
have? HINT [See Example 2.]
13
Need Help?
DETAILS
Master It
Submit Assignment Save Assignment Progress
MY NOTES
ASK YOUR TEACHER
PRACTICE ANOTHER](https://media.kunduz.com/media/sug-question/raw/57429604-1657622127.7535388.jpeg?w=256)
Math
Probability9. [0/1 Points]
PREVIOUS ANSWERS WAS WANEFMAC7 7.3.021.MI.
While selecting candy for students in his class, Professor Murphy must choose between gummy candy and licorice nibs. Gummy candy packets come in five sizes, while packets of licorice nibs come
in two. If he chooses gummy candy, he must select gummy bears, gummy worms, or gummy dinos. If he chooses licorice nibs, he must choose between red and black. How many choices does he
have? HINT [See Example 2.]
13
Need Help?
DETAILS
Master It
Submit Assignment Save Assignment Progress
MY NOTES
ASK YOUR TEACHER
PRACTICE ANOTHER

Math
ProbabilityAssume that blood pressure readings are normally distributed with a mean of 135 and a standard deviation of 4.8. If 35 people are randomly selected, find the probability that their mean blood pressure will be less than 137.
Math
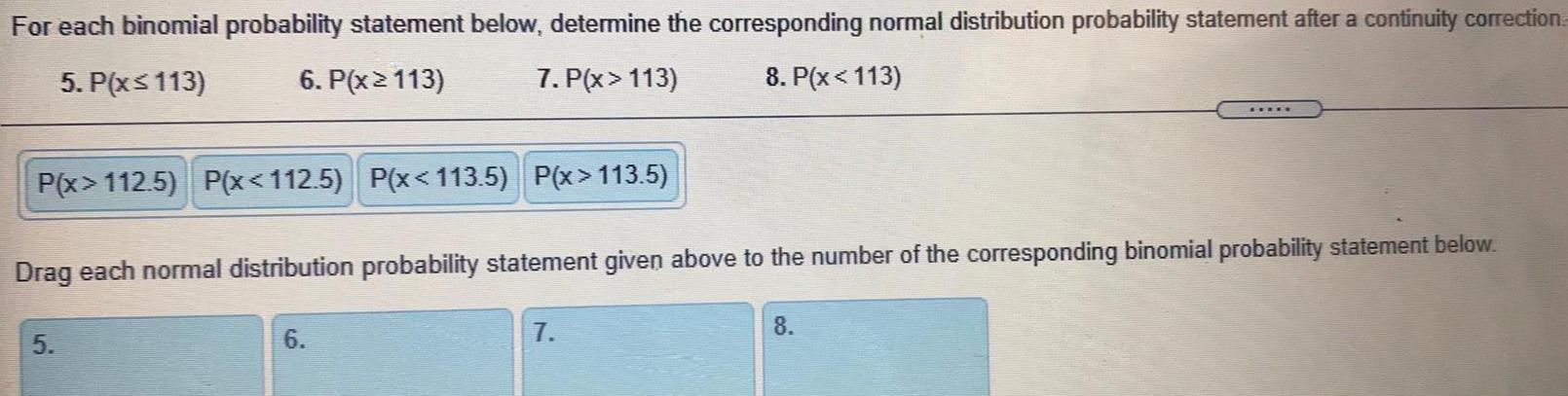
ProbabilityFor each binomial probability statement below, determine the corresponding normal distribution probability statement after a continuity correction
5. P(x≤ 113)
6. P(x≥113)
7. P(x > 113)
8. P(x<113)
P(x>112.5) P(x<112.5) P(x<113.5) P(x>113.5)
Drag each normal distribution probability statement given above to the number of the corresponding binomial probability statement below.

Math
ProbabilityIn one lottery, a player wins the jackpot by matching all five distinct numbers drawn in any order from the white balls (1 through 41) and matching the number on the gold ball (1 through 33). If one ticket is purchased, what is the probability of winning the
jackpot?
The probability of winning the jackpot with one ticket is
(Type an integer or a simplified fraction.)
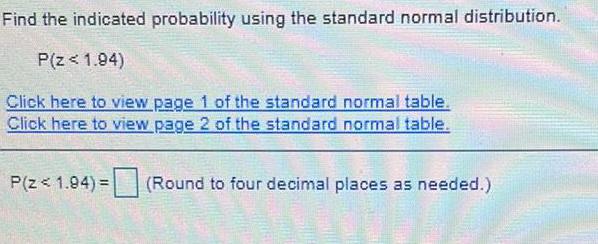
Math
ProbabilityFind the indicated probability using the standard normal distribution.
P(Z < 1.94)
P(Z < 1.94) = (Round to four decimal places as needed.)

Math
ProbabilityA box contains 12 transistors, 4 of which are defective. If 4 are selected at random, find the probability of the statements below.
a. All are defective
b. None are defective
a. The probability is
(Type a fraction. Simplify your answer.)

Math
ProbabilityA lottery consists of 36 numbers. You must pick the six winning numbers to win. What is the chance of you winning?
Enter your answer as an exact value.

Math
ProbabilityA hand consists of 4 cards from a well-shuffled deck of 52 cards.
a. Find the total number of possible 4-card poker hands.
b. A spade flush is a 4-card hand consisting of all spade cards. Find the number of possible spade flushes.
c. Find the probability of being dealt a spade flush.
a. There are a total of poker hands.
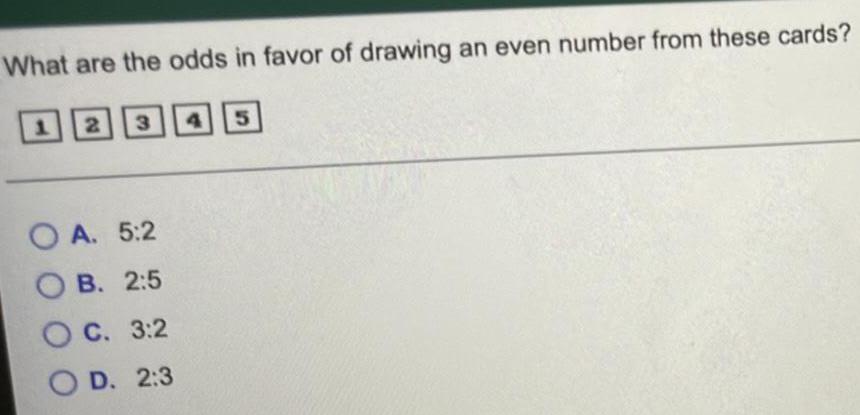
Math
ProbabilityWhat are the odds in favor of drawing an even number from these cards?
1 2 3 4 5
A. 5:2
B. 2:5
C. 3:2
D. 2:3
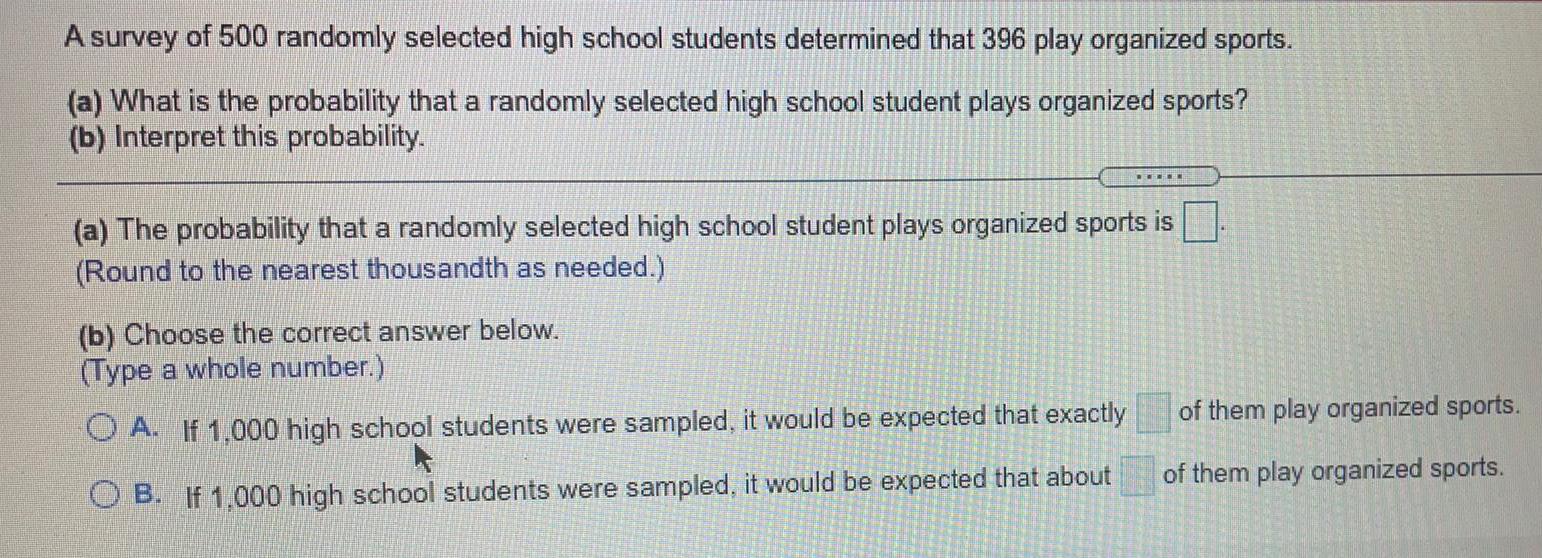
Math
ProbabilityA survey of 500 randomly selected high school students determined that 396 play organized sports.
(a) What is the probability that a randomly selected high school student plays organized sports?
(b) Interpret this probability.

Math
ProbabilityThere are 3 cards in a hat; one is a king, one is a queen, and one is an ace. Two cards are to be selected at random with replacement. Using a tree diagram, obtain the sample space for the experiment. List the elements that make up the sample space.
A. KKQ, KAK, QQQ, KQ, AAK
B. KK, KQ, KA, QK, QQ, QA, AK, AQ, AA
C. KK, KQ, KA, QQ, QA, AQ, A A
D. KQ,KA, QK, QA, AK, AQ

Math
ProbabilityANSWER THE FOLLOWING PROBABILITY TO ODDS OR ODDS TO PROBABILITY PROBLEMS.
a) HORSE RACING - THE ODDS AGAINST BUTTERMILK WINNING THE TRIPLE CROWN IN HORSE RACING ARE 82:3. FIND THE PROBABILITY THAT BUTTERMILK WINS THE TRIPLE CROWN.
b) JITTERBUG CONTEST - THE PROBABILITY THAT BOB AND SUE NENNO WILL WIN THE JITTERBUG CONTEST IS 0.7. FIND THE ODDS IN FAVOR OF THEM WINNING.

Math
ProbabilityA basket is filled with 7 white eggs and 14 brown eggs. Half of the brown eggs are cracked. An egg is randomly selected from the basket. What is the probability that it is a cracked, brown egg?
Write your answer as a fraction.
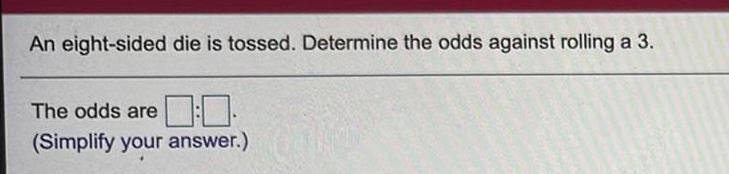
Math
ProbabilityAn eight-sided die is tossed. Determine the odds against rolling a 3.
The odds are
(Simplify your answer.)
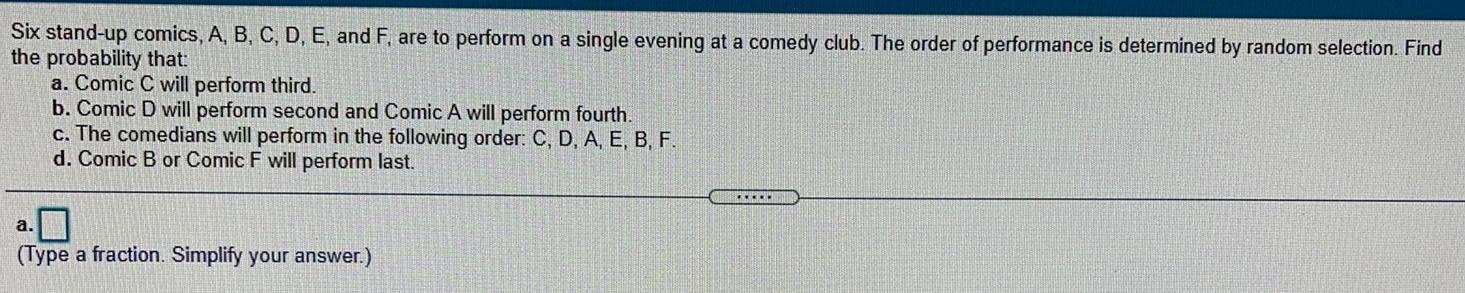
Math
ProbabilitySix stand-up comics, A, B, C, D, E, and F, are to perform on a single evening at a comedy club. The order of performance is determined by random selection. Find the probability that:
a. Comic C will perform third.
b. Comic D will perform second and Comic A will perform fourth.
c. The comedians will perform in the following order: C, D, A, E, B, F.
d. Comic B or Comic F will perform last.

Math
ProbabilityA 12-sided die is rolled. Find the probability of rolling an odd number. The set of equally likely outcomes is shown below. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Math
ProbabilityA number cube with faces labeled from 1 to 6 will be rolled once.
The number rolled will be recorded as the outcome.
Give the sample space describing all possible outcomes.
Then give all of the outcomes for the event of rolling a number from 2 to 4.
If there is more than one element in the set, separate them with commas.

Math
ProbabilityA die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting exactly five twos. Round to three decimal places.
A. 0.129
B. 0.921
C. 0.003
D. 0.083
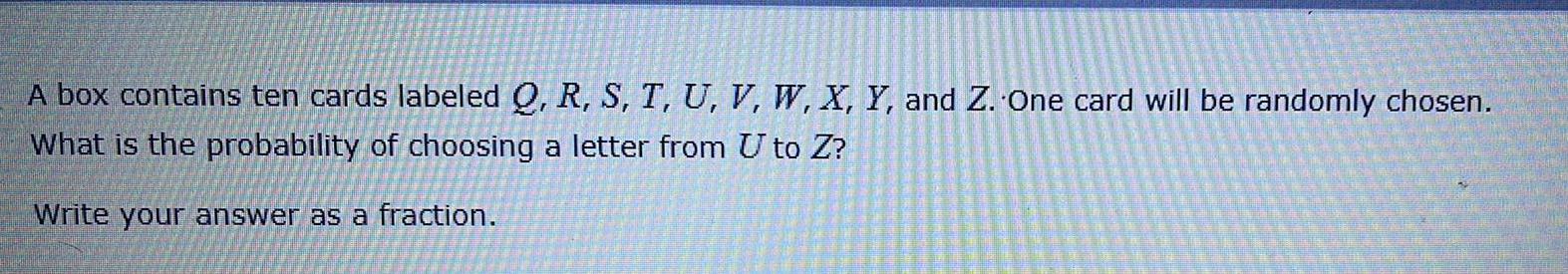
Math
ProbabilityA box contains ten cards labeled Q, R, S, T, U, V, W, X, Y, and Z. One card will be randomly chosen.
What is the probability of choosing a letter from U to Z?
Write your answer as a fraction.

Math
ProbabilityEXPECTED ATTENDANCE - FOR A SHOWING OF A SPECIFIC MOVIE, AN AMC THEATER ESTIMATES THAT 120 PEOPLE WILL ATTEND IF IT IS NOT RAINING. IF IT IS RAINING, THE THEATER ESTIMATES THAT 200 PEOPLE WILL ATTEND. THE METEOROLOGIST PREDICTS A 70% CHANCE OF RAIN TOMORROW. DETERMINE THE EXPECTED NUMBER OF PEOPLE WHO WILL ATTEND THE MOVIE.

Math
ProbabilityAssume that a set of test scores is normally distributed with a mean of 80 and a standard deviation of 20. Use the 68-95-99.7 rule to find the following quantities.
a. The percentage of scores less than 80 is%.
(Round to one decimal place as needed.)

Math
ProbabilityCat Behavior A report stated that the average number of times a cat returns to its food Bowl during the day is 38. Assuming the variable is normally distributed with a standard deviation of 4, what is the probability that a cat would return to its dish between 35 and 40 times a day? Round the final answer to four decimal places and intermediate z-value calculations to 2 decimal places.

Math
ProbabilityIf the probability that an event will occur is 2/7 then the probability that the event will not occur is 5/7 and the odds in favor of the event occurring are .....
The odds are

Math
ProbabilitySuppose that 30% of students go to sleep on time. If a student went to sleep on time, the probability that they felt well rested was 0.80. Further, the probability that a student both did not go to sleep on time and felt well rested was 0.20. (a)) Find the probability that a student felt well rested.

Math
ProbabilitySuppose the length a cat takes a nap (the length of a cat nap) has a population mean of 3 hours, with population standard deviation 1.75 hours. Assume the length of a cat nap is normally distributed.
(a) Find the probability that a randomly selected cat takes a nap over 4 hours in length.

Math
ProbabilityHarry Potter is at Ollivanders Wand Shop. As we all know, the wand must choose the wizard, so Harry cannot make the choice himself. He interprets the wand selection as a random process so he can determine the probabilities of different outcomes.
The wood types available are holly, elm, maple, and wenge. The core materials on offer are phoenix feather,
unicorn hair, dragon scale, raven feather, and thestral tail.
Let A be the event that Harry is chosen by a wand made of holly and B be the event that he is chosen by a wand with a dragon scale core.
What is P(A or B), the probability that Harry is chosen by a wand made of holly or a wand with a dragon scale core?

Math
ProbabilityLet's look back at our bet on either "Aces" or "Boxcars". We win if we roll a sum of 2 for "Aces" or
a sum of 12 for "Boxcars". Let's place a $10 bet on "Boxcars"!
a) What is the probability of winning?
P(W) =
b) What is the probability of losing?
P(L) =
c) The payoff odds are 30:1. What does this mean?

Math
ProbabilityIn a race in which six automobiles are entered and there are no ties, in how many ways can the first three finishers come in?

Math
ProbabilityAbdul rolls a fair six-sided die and a fair four-sided die simultaneously. The sample space of all possible outcomes is shown below.
Let A be the event that the six-sided die is three and B be the event that Abdul rolls doubles (rolls the same number on each die).
What is P(A or B), the probability that the six-sided die is three or Abdul rolls doubles?

Math
ProbabilityScores of an IQ test have a bell-shaped distribution with a mean of 100 and a standard deviation of 18. Use the empirical rule to determine the following.
(a) What percentage of people has an IQ score between 82 and 118?
(b) What percentage of people has an IQ score less than 46 or greater than 154?
(c) What percentage of people has an IQ score greater than 136?

Math
ProbabilityAccording to recent research, 41% of Americans have less than $375 in the bank for an emergency. Let p be the proportion of people who have less than $375 in the bank for an emergency in a random sample of 86 Americans. Determine the probability that the proportion of people in a random sample of 86 Americans who have less than $375 in the bank for an emergency is within 7% of the population proportion. Round the solution to four decimal places. P(p within 7% of the population proportion) Determine the probability that the proportion of people in a random sample of 86 Americans who have less than $375 in the bank for an emergency is less than the population proportion by 9% or more. Round the solution to four decimal places. P(p less than the population proportion by 9% or more) : =

Math
ProbabilityA distribution is given as X~ U(0, 12).
Find P(x > 3). (Enter an exact number as an integer, fraction, or decimal.)

Math
ProbabilitySuppose that the random variables X and Y have the following joint probability density function.
f(x, y) = ce^-3x-7y, 0 < y < x.
(a) Find P(X < 2, Y < 1/8).
(b) Find the marginal probability distribution of X.

Math
ProbabilityThe weight of a sophisticated running shoe is normally distributed with a mean of 13 ounces. (a) What must the standard deviation of weight be in order for the company to state that 96% of its shoes weight less than 14 ounces?
(b) Suppose that the standard deviation is actually 0.81. If we sample 6 such running shoes, find the probability that exactly 4 of those shoes weigh more than 14 ounces.

Math
ProbabilityThe organizers of a marathon event estimate that
the time that it takes for a race participant to
finish the race is normally distributed with a
mean of 270 minutes and a standard deviation of
10 minutes.
Write the percentage of runners who finish the
race within 4 hours and 45 minutes. Round your
answer to the nearest whole number.

Math
ProbabilityOf the cartons produced by a company, 7% have a puncture, 3% have a smashed corner, and 0.7% have both a puncture and a smashed corner.
Find the probability that a randomly selected carton has a puncture or a smashed comer.
The probability that a randomly selected carton has a puncture or a smashed corner
(Type an integer or a decimal. Do not round.)

Math
ProbabilityThe probability that an event will happen is P(E): 25/31. Find The probability that the event will not happen is
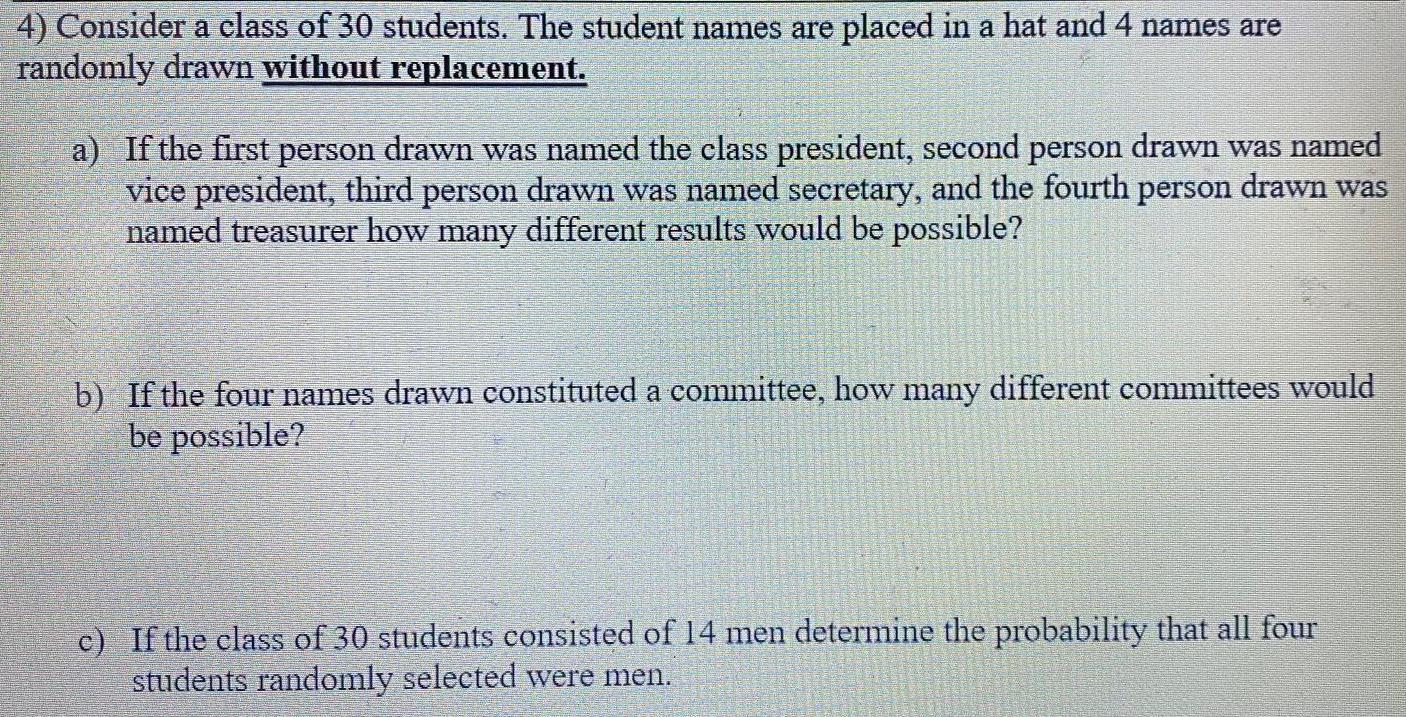
Math
Probability4) Consider a class of 30 students. The student names are placed in a hat and 4 names are randomly drawn without replacement.
a) If the first person drawn was named the class president, second person drawn was named vice president, third person drawn was named secretary, and the fourth person drawn was named treasurer how many different results would be possible?
b) If the four names drawn constituted a committee, how many different committees would be possible?
c) If the class of 30 students consisted of 14 men determine the probability that all four students randomly selected were men.

Math
ProbabilityWith one method of a procedure called acceptance sampling, a sample of items is randomly selected without replacement and the entire batch is rejected if there is at least one defective unit. The ABCD Electronics Company has just manufactured 5500 write-rewrite CDs, and 130 are defective. If 5 of these CDs are randomly selected and tested, what is the probability that the entire batch will be rejected? Report the answer as a percent with one decimal place accuracy.

Math
ProbabilityIn a sample of 800 U.S. adults, 205 think that most celebrities are good role models. Two U.S. adults are selected from this sample without replacement. Complete parts (a) through (c).

Math
ProbabilitySide effects: A new medical procedure produces side effects in 27% of the patients who receive it. In a clinical trial, 80 people undergo the procedure.
Cumulative Normal Distribution Table or
What is the probability that 19 or fewer experience side effects? Approximate using the normal curve. Use the
technology. Round your answer to four decimal places.
The probability that 19 or fewer patients experience side effects is
X
Ś
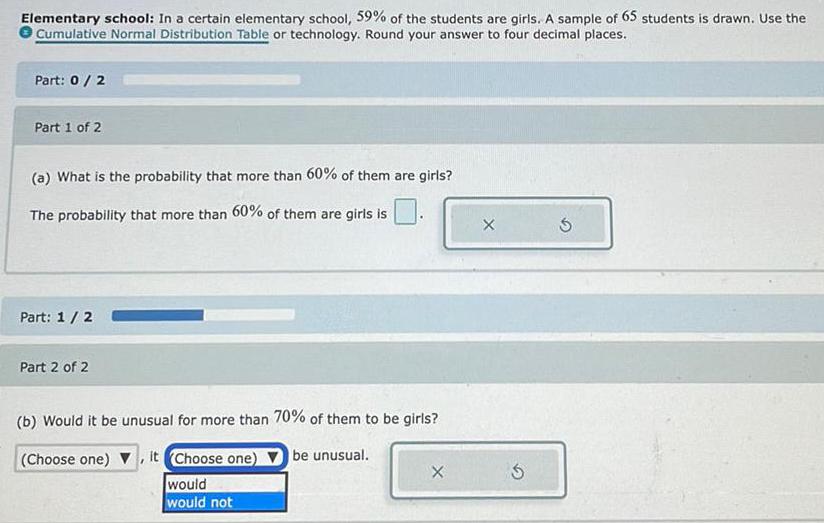
Math
ProbabilityIn a certain elementary school, 59% of the students are girls. A sample of 65 students is drawn. Use the Cumulative Normal Distribution Table or technology. Round your answer to four decimal places.
(a) What is the probability that more than 60% of them are girls?
The probability that more than 60% of them are girls is
(b) Would it be unusual for more than 70% of them to be girls?
Math
ProbabilityA box contains three cards. On one card there is a sun, on another card there is a question mark, and on the third card there is an apple. Two cards are selected with replacement.
On your scratch paper draw the tree diagram and answer the following questions.
How many points in the sample space?
What is the probability that 2 apples are selected.
What is the probability that a sun and then a question mark are selected?
What is the probability that atleast one apple is selected?