Probability Questions and Answers
Math
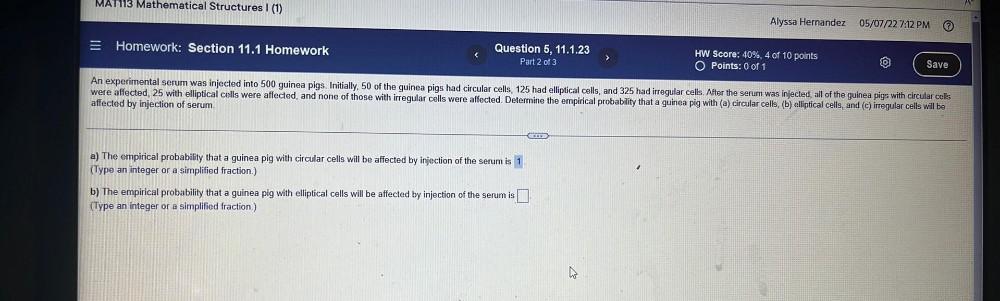
ProbabilityAn experimental serum was injected into 500 guinea pigs. Initially, 50 of the guinea pigs had circular cells, 125 had elliptical cells, and 325 had irregular cells. After the serum was injected, all of the guinea pigs with circular cells were affected, 25 with elliptical cells were affected, and none of those with irregular cells were affected. Determine the empirical probability that a guinea pig with (a) circular cells, (b) elliptical cells, and (c) irregular cells will be affected by injection of serum.
a) The empirical probability that a guinea pig with circular cells will be affected by injection of the serum is 1.
b) The empirical probability that a guinea pig with elliptical cells will be affected by injection of the serum is_____.
Math
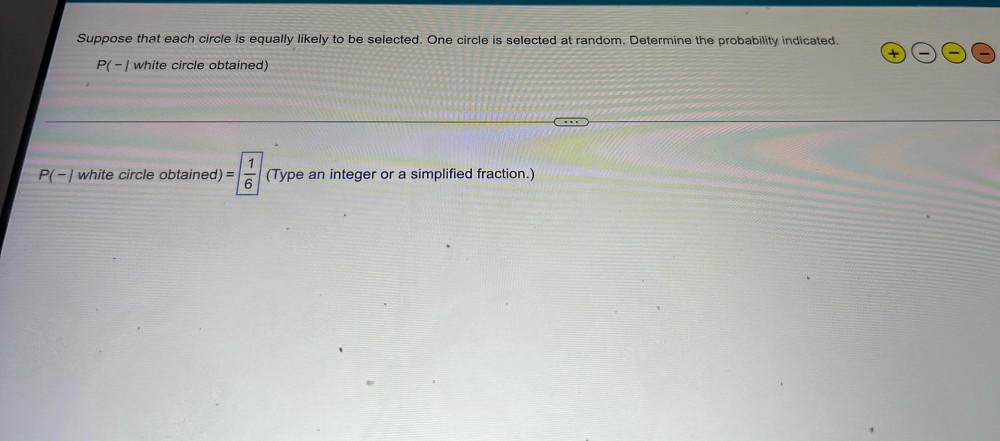
ProbabilitySuppose that each circle is equally likely to be selected. One circle is selected at random. Determine the probability indicated.
P (- |white circle obtained)
Math
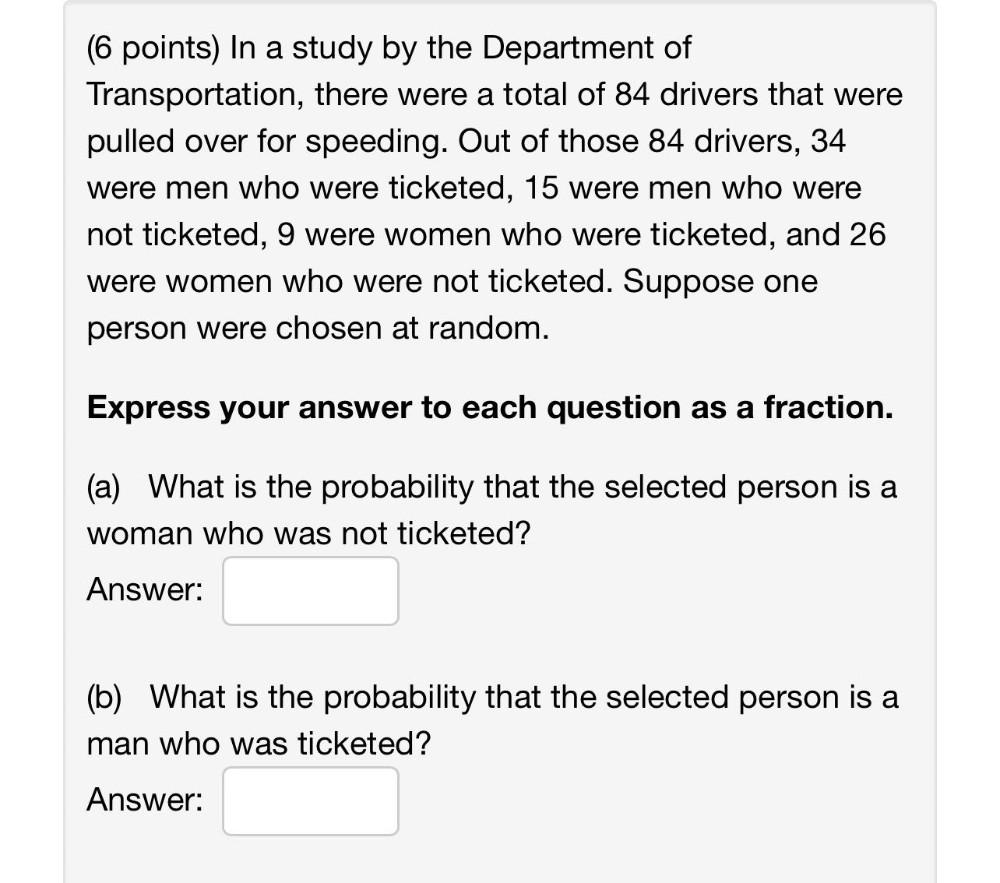
ProbabilityIn a study by the Department of Transportation, there were a total of 84 drivers that were pulled over for speeding. Out of those 84 drivers, 34 were men who were ticketed, 15 were men who were not ticketed, 9 were women who were ticketed, and 26 were women who were not ticketed. Suppose one person were chosen at random.
Express your answer to each question as a fraction.
(a) What is the probability that the selected person is a
woman who was not ticketed?
Answer:
(b) What is the probability that the selected person is a
man who was ticketed?
Answer:
Math
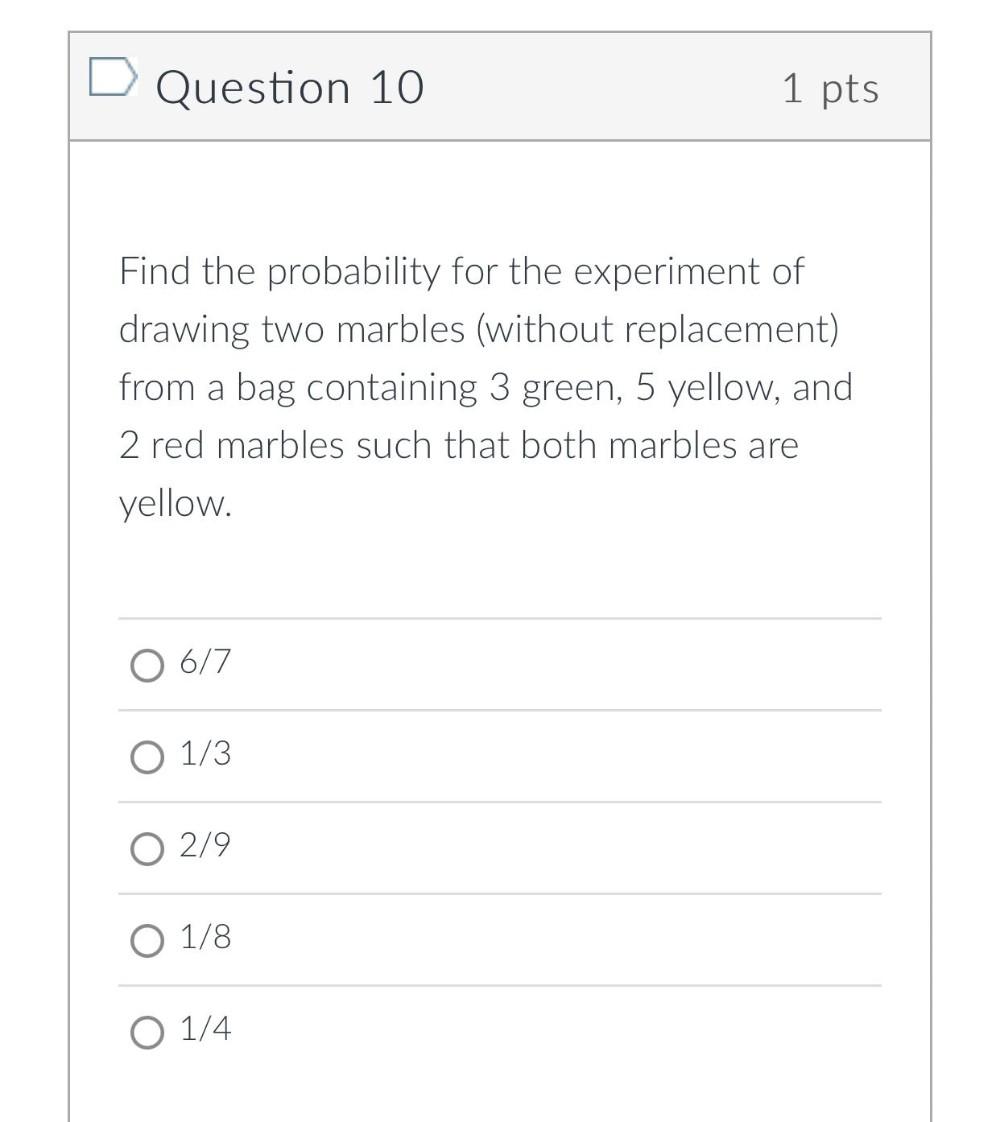
ProbabilityFind the probability for the experiment of drawing two marbles (without replacement) from a bag containing 3 green, 5 yellow, and 2 red marbles such that both marbles are yellow.
○ 6/7
○ 1/3
○ 2/9
○ 1/8
○ 1/4

Math
ProbabilityLet X1, X2,..., Xm be independent and identically distributed random variables, each following the Bernoulli(p) distribution, and let X = X_1 + X_2 + ... + X_m.
Which one of the following statements is always true?
Select one:
A. X follows the negative binomial distribution with parameters m and p
B. X follows the binomial distribution with parameters m and p
C. X follows the geometric distribution with parameter p
D. X follows the Bernoulli distribution with parameter p

Math
ProbabilityHeights of fourth-graders are normally distributed with a mean of 52 inches and a standard deviation of 3.5 inches. Find the probability that a randomly selected fourth-grader is taller than 60 inches.
2.3%
5%
3%
1.1%
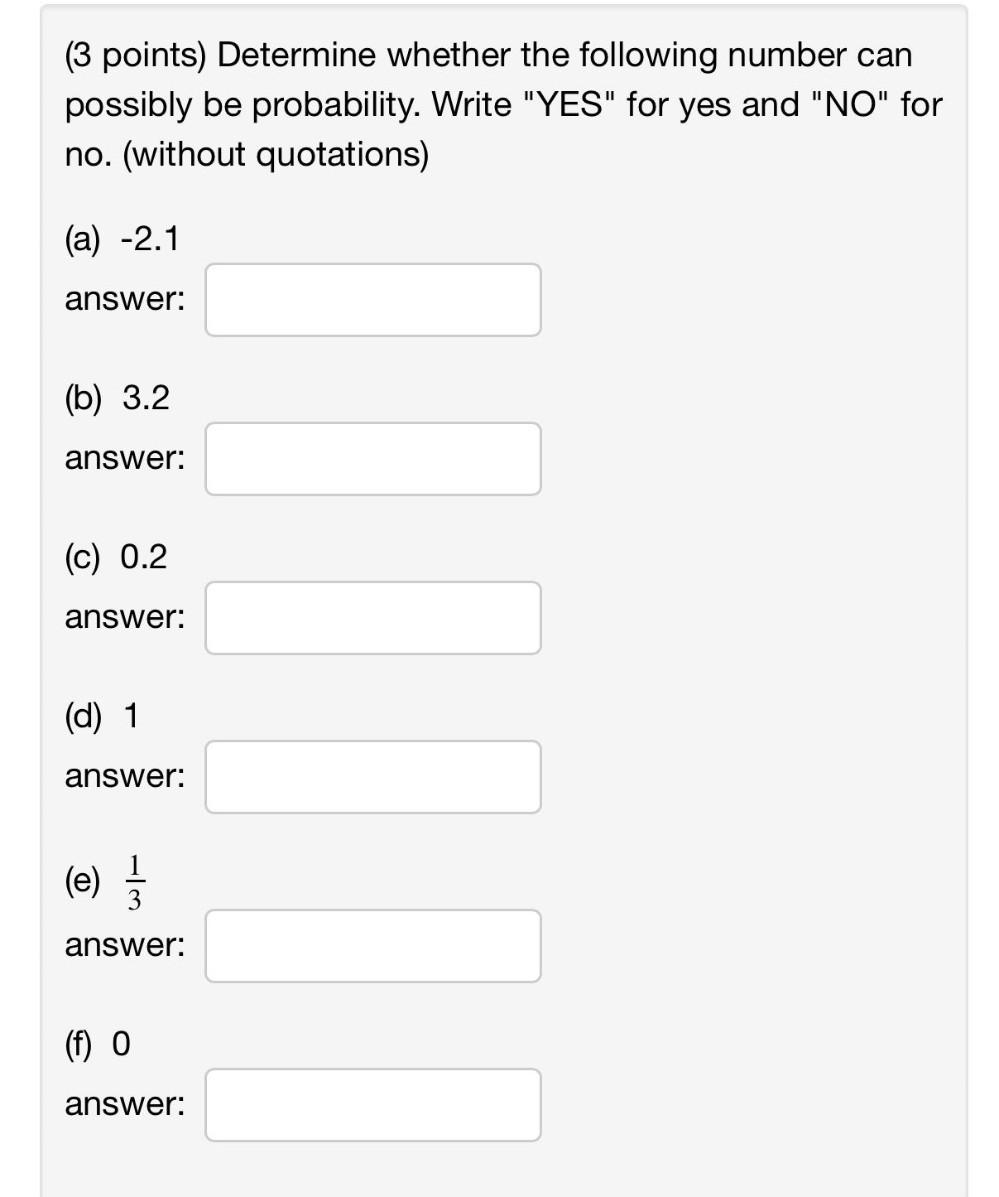
Math
ProbabilityDetermine whether the following number can possibly be probability. Write "YES" for yes and "NO" for no. (without quotations)
(a) -2.1
answer:
(b) 3.2
answer:
(c) 0.2
answer:
(d) 1
answer:
(e) 1/3
answer:
(f) 0
answer:
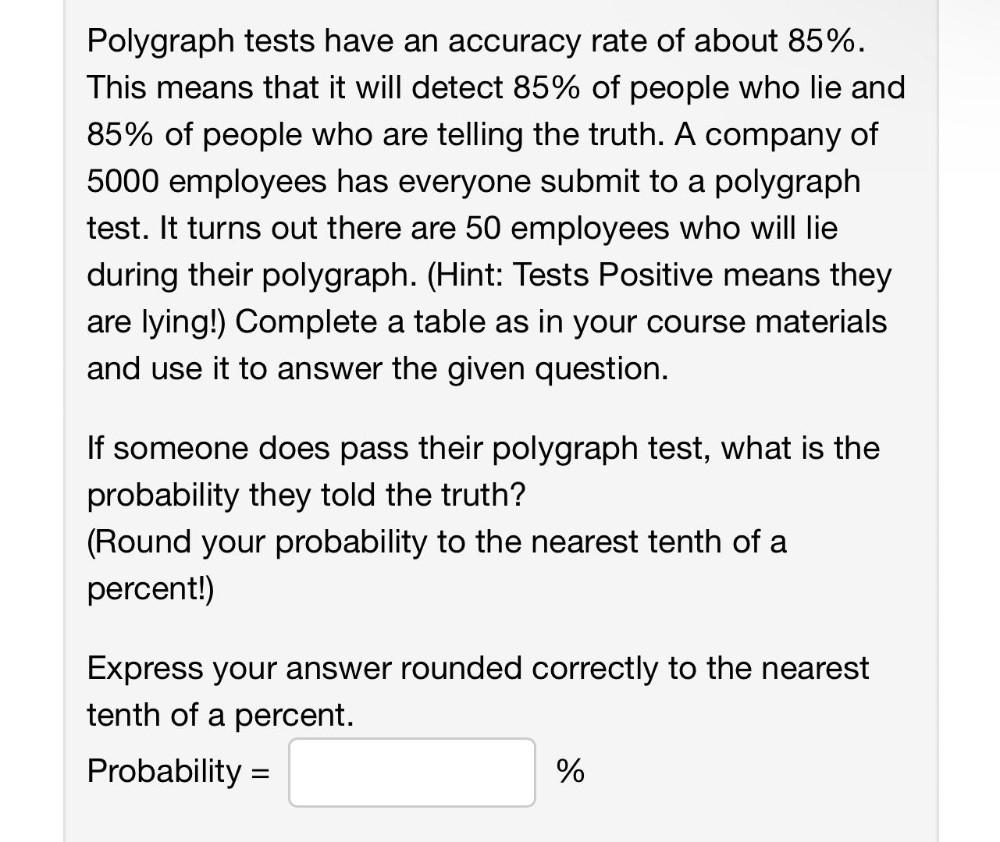
Math
ProbabilityPolygraph tests have an accuracy rate of about 85%. This means that it will detect 85% of people who lie and 85% of people who are telling the truth. A company of 5000 employees has everyone submit to a polygraph
test. It turns out there are 50 employees who will lie during their polygraph. (Hint: Tests Positive means they are lying!) Complete a table as in your course materials and use it to answer the given question.
If someone does pass their polygraph test, what is the probability they told the truth? (Round your probability to the nearest tenth of a percent!)
Express your answer rounded correctly to the nearest tenth of a percent.
Probability =
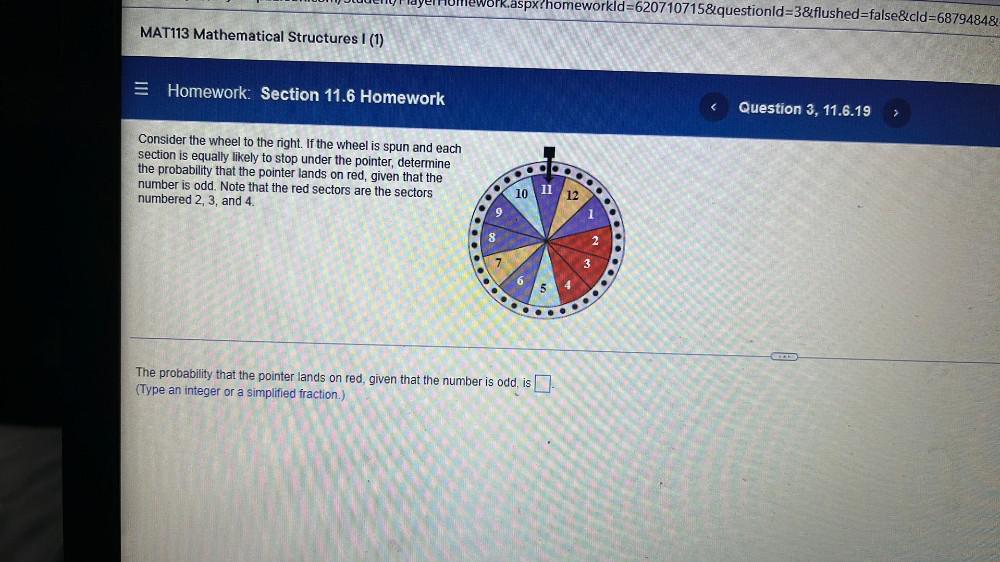
Math
ProbabilityConsider the wheel to the right. If the wheel is spun and each section is equally likely to stop under the pointer, determine the probability that the pointer lands on red, given that the number is odd. Note that the red sectors are the sectors
numbered 2, 3, and 4.
The probability that the pointer lands on red, given that the number is odd, is
(Type an integer or a simplified fraction.)

Math
ProbabilityProbability problems that contain the words and or or are considered probability problems.
Probability problems that contain the words and or or are considered
__________probability problems.
a)mutually exclusive
b)dependent event
c)independent event
d)compound

Math
ProbabilityOne hundred people were surveyed, and one question pertained to their educational background. The results of this question and their genders are given in the following table.
Female Male Total
College degree 24 26 50
No college degree 15 35 50
Total 39 61 100
If a person is selected at random from those surveyed, find the probability if each of the following events.
1. The person is female or has a college degree.
Answer: ▢
2. The person is female and has a college degree.
Answer: ▢
3. The person is female or does not have a college degree.
Answer: ▢
4. The person is female and does not have a college degree.
Answer: ▢
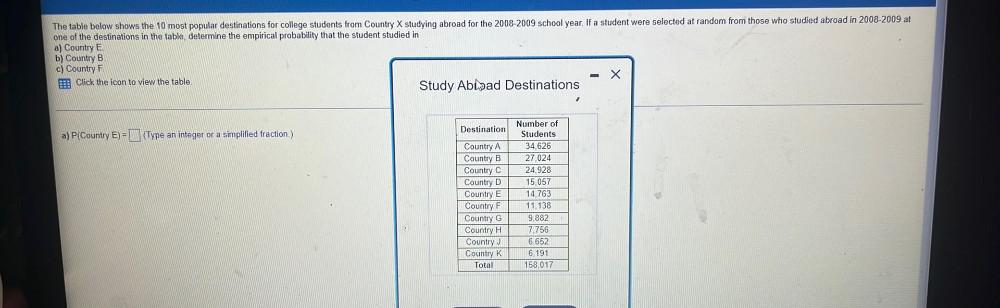
Math
ProbabilityThe table below shows the 10 most popular destinations for college students from Country X studying abroad for the 2008-2009 school year. If a student were selected at random from those who studied abroad in 2008-2009 at one of the destinations in the table, determine the empirical probability that the student studied in
a) Country E.
b) Country B.
c) Country F.

Math
ProbabilityA container holds 2 yellow balls and 4 red balls. A ball will be drawn, its color noted, and replaced. A second ball will be drawn, and its color recorded. Do not
reduce.
a. Draw a two-stage tree diagram for this. Indicate the probability on each branch
b. Find the probability of drawing 2 red balls:______________
c. Find the probability of drawing at least 1 red:________________
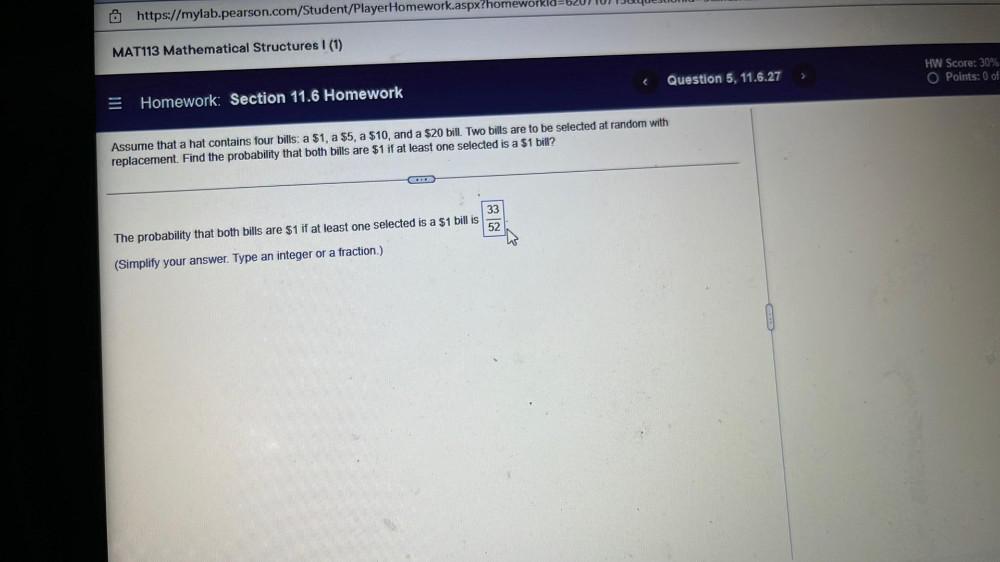
Math
ProbabilityAssume that a hat contains four bills: a $1, a $5, a $10, and a $20 bill. Two bills are to be selected at random with replacement. Find the probability that both bills are $1 if at least one selected is a $1 bill?
The probability that both bills are $1 if at least one selected is a $1 bill is ______
![Find the indicated conditional probability using the following two-way table:
Grade Drive to school Take the bus Walk
Sophomore 2 25 3
Junior 13 20 2
Senior 25 5 5
P( Walk to school | Senior) = [?]
Round to the nearest hundredth.](https://media.kunduz.com/media/sug-question/raw/77413218-1658832086.1728559.jpeg?w=256)
Math
ProbabilityFind the indicated conditional probability using the following two-way table:
Grade Drive to school Take the bus Walk
Sophomore 2 25 3
Junior 13 20 2
Senior 25 5 5
P( Walk to school | Senior) = [?]
Round to the nearest hundredth.

Math
ProbabilityA local restaurant manager wants to survey customers about the service they receive. Each night the manager randomly chooses a number between 1 and 10. He then gives a survey to that customer, and to every 10th customer after them to fill it out before they love.
Cluster Sample
Systematic Sample
Simple Random Sample
Convenience Sample

Math
ProbabilityIn a survey of families, the following data were obtained relating to the number of pets in their household:
Number of pets Frequency
0 10
1 15
2 10
3 10
4 5
total 50
What is the probability of calling a random family from the list that has less than 3 pets?
What is the probability of calling a random family from the list that has less than 3 pets?
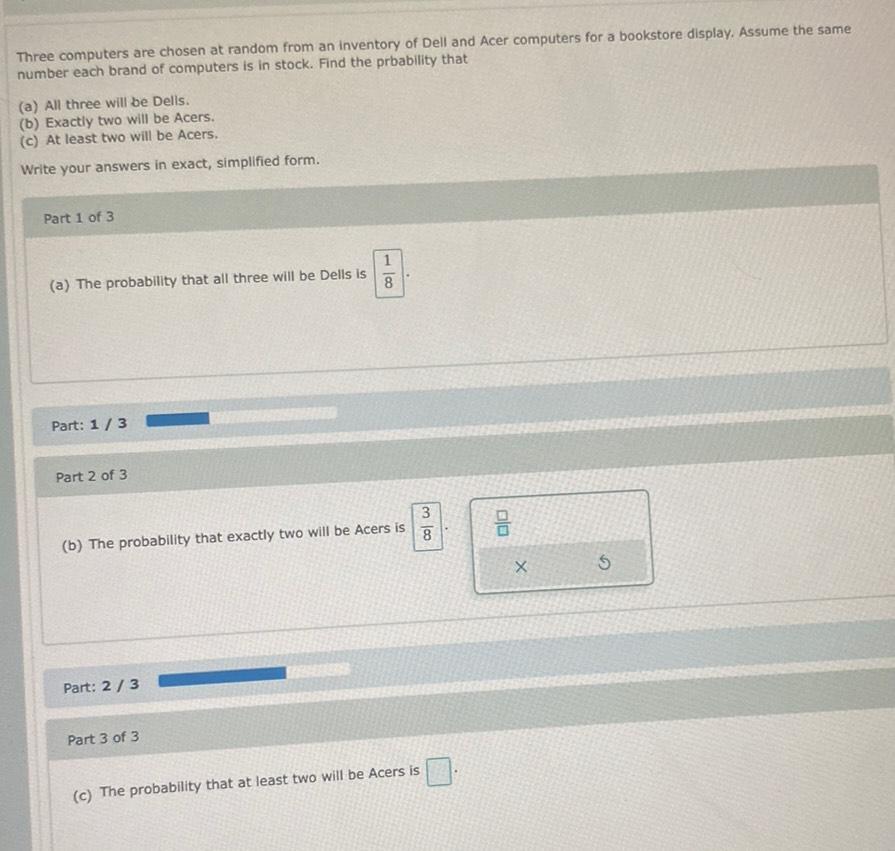
Math
ProbabilityThree computers are chosen at random from an inventory of Dell and Acer computers for a bookstore display. Assume the same number each brand of computers is in stock. Find the probability that
(a) All three will be Dells.
(b) Exactly two will be Acers.
(c) At least two will be Acers.

Math
ProbabilityInside a bag there are 3 green balls, 2 red balls and 2 yellow balls. Two balls are randomly drawn without replacement. Calculate the probability of drawing one green ball and one yellow ball. The tree diagram has been started. ▢

Math
ProbabilityFind the probability for the experiment of selecting one card from a standard deck of 52 playing cards such that the card is a 10 or higher (aces are low).
4/13
11/13
9/26
12/13
3/13

Math
ProbabilityDescribe how and when to use multiplication rule 1, P (A and B)=P(A) . P(B), and how and when use multiplication rule 2, P(A and B) = P(A) P(B, given that A has already occured).
Use multiplication rule 1 when two events are joined by "and" and the events are. Use multiplication rule 2 when the events are joined by "and" and the events are .
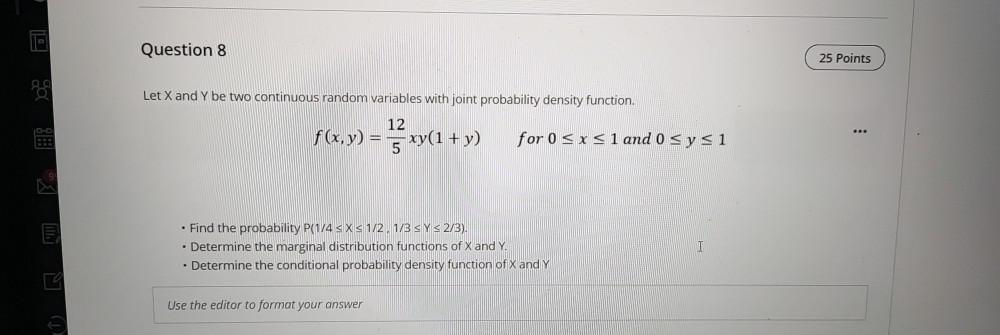
Math
ProbabilityLet X and Y be two continuous random variables with joint probability density function
f(x,y) = 12/5xy(1+y) for 0 ≤x ≤1 and 0 ≤ y ≤ 1
• Find the probability P(1/4 ≤ X ≤1/2, 1/3 ≤ Y ≤ 2/3).
• Determine the marginal distribution functions of X and Y
• Determine the conditional probability density function of X and Y

Math
ProbabilityDifferent shapes are drawn on cards and then the cards are placed in a bag. The number of cards for each shape is shown in the table.
Shape octagon square circle
Number of cards 12 27 91
What is the probability that a randomly selected card has a circle drawn on it? Write your answer as a fraction in simplest form.
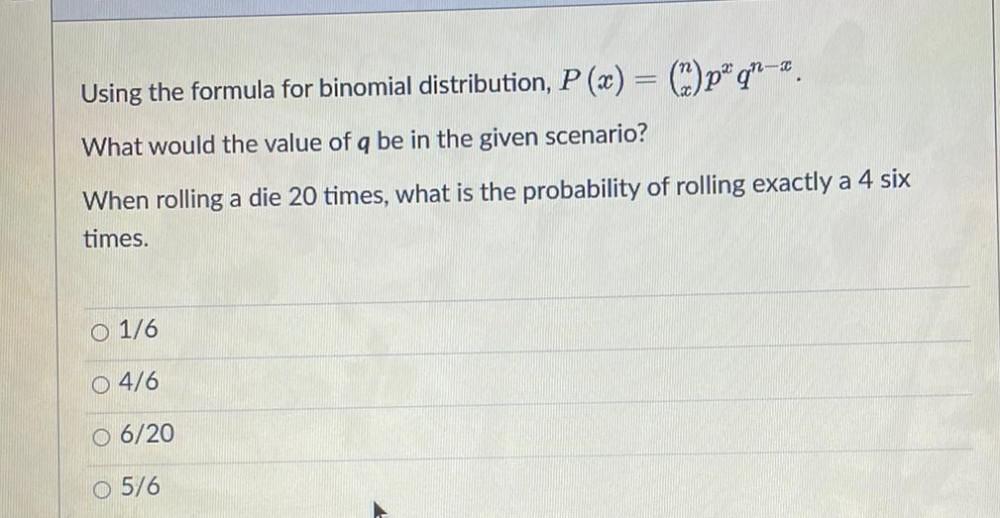
Math
ProbabilityUsing the formula for binomial distribution, P(x) = (n x)px qn-x.
What would the value of q be in the given scenario?
When rolling a die 20 times, what is the probability of rolling exactly a 4 six
times.
1/6
4/6
6/20
5/6
Math
ProbabilityAn airline is planning its staffing needs for the next year. If a new route is approved, it will hire 935 new employees. If a new route is not granted, it will hire only 175 new employees. If the probability that a new route will be granted is 0.4, what is the expected number of new employees to be hired by the airline?
Math
ProbabilityA speaker is talking about the principle of charity, and suggests that a person
who is truly charitable will offer money to someone in need unreservedly. He
illustrates this by saying that one should open their wallet and hand money to
another person without looking at how much money they are holding. Suppose
this speaker had five bills in his wallet: two $20, one $10, and two $5. If he were
to choose one bill at random to give away to the next person who asked him,
what is the expected value of his handout?
Math
ProbabilitySam's Pizza advertises that their delivery times are the best in town. If their delivery times are normally distributed with mean 30 minutes and standard deviation 5 minutes, what is the probability that your pizza from Sam's will take more than 37 minutes to be delivered? Justify your answer.

Math
ProbabilityA drug testing company advertises a test for steroids that is 94.5% effective at detecting steroid use. It has a true negative effectiveness of 94%. Suppose 12% of 10,000 professional cyclists are believed to be using steroids. Suppose a cyclist tests negative for steroid use. What is the probability that he's using steroids? (Round your probability to the nearest hundredth of a percent!)

Math
ProbabilityUse common sense to determine whether the given event is impossible; possible, but very unlikely; or possible and likely.
A solar eclipse occurs on your birthday.
Impossible
Possible, but very unlikely
Possible and likely
Math
ProbabilityFor the two circumstances below, explain which type of probability (empirical,
subjective, theoretical) is being used to make the prediction. If more than one
type of probability is involved, explain which elements of the process use which of the methods.
,a. A scientist studying ants builds an ant farm and maps the routes they travel throughout the course of a week through careful observation. Later the scientist uses these observations to generate an interactive map of a natural environment that lists the probability of finding ants in any given location at a particular time.

Math
ProbabilityA six-sided number cube is tossed and a coin is flipped. The sample space is {1H, 2H, 3H, 4H, 5H, 6H, 1T, 2T, 3T, 4T, 5T, 6T}.
What is the probability of rolling an even number and flipping tails?
Enter your answer, as a fraction in simplest form, in the box.

Math
ProbabilityOut of 35 students, 14 pick apples as their favorite snack, 21 pick M&M's as their favorite snack, and 10 choose both. (Leave answers in fraction form. Do not
reduce.
a. Fill in the Venn diagram for this.
b. Find P(apple only) ________
c. Find P(apple and M&M's)________
d. Find P(student did not choose apple).________________
e. Find P(the student did not choose either)_______________
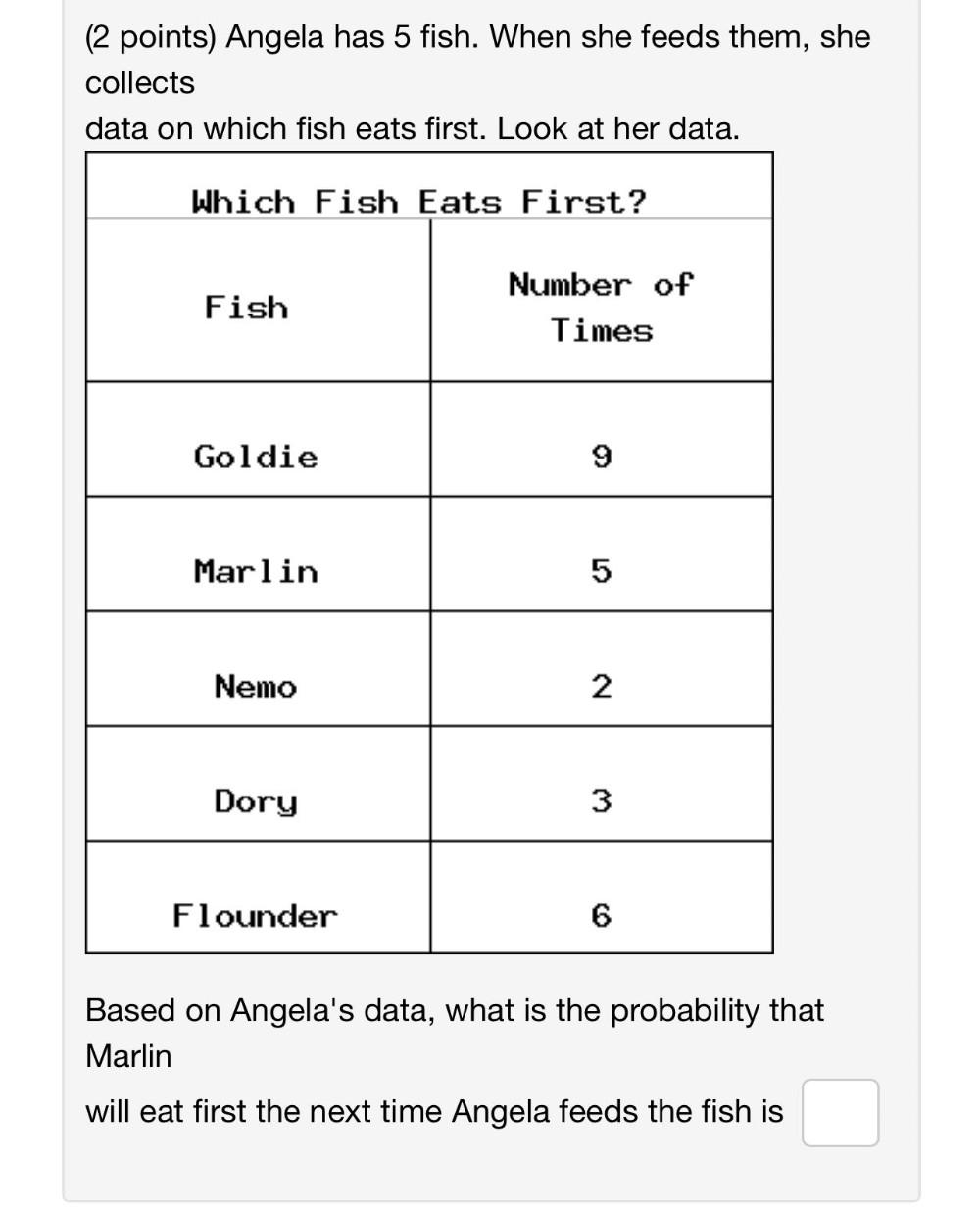
Math
ProbabilityAngela has 5 fish. When she feeds them, she collects data on which fish eats first. Look at her data.
Which Fish Eats First?
Fish Number of
Times
Goldie 9
Marlin 5
Nemo 2
Dory 3
Flounder 6
Based on Angela's data, what is the probability that Marlin will eat first the next time Angela feeds the fish is ▢
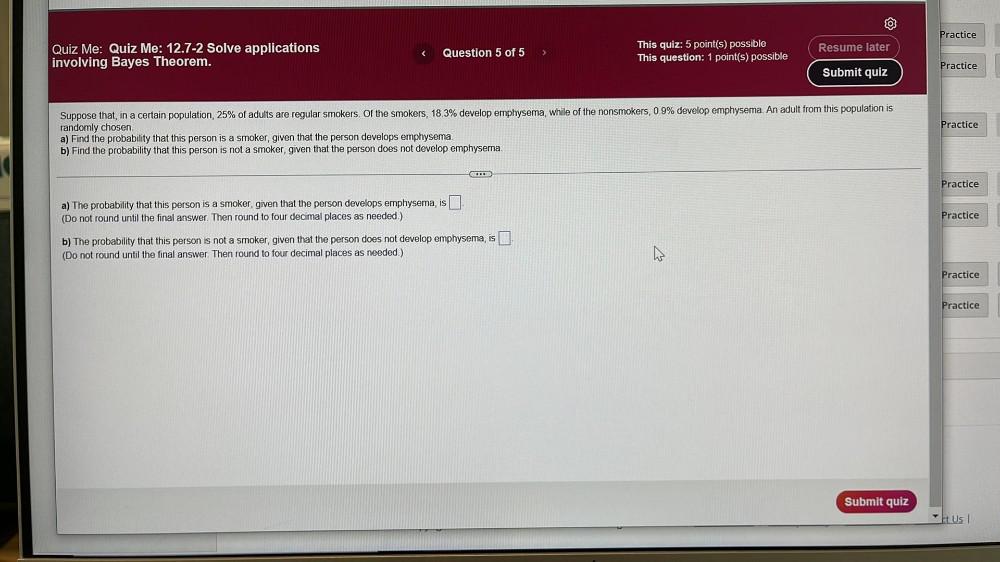
Math
ProbabilitySuppose that, in a certain population, 25% of adults are regular smokers. Of the smokers, 18.3% develop emphysema, while of the nonsmokers, 0.9% develop emphysema. An adult from this population is randomly chosen.
a) Find the probability that this person is a smoker, given that the person develops emphysema.
b) Find the probability that this person is not a smoker, given that the person does not develop emphysema.
a) The probability that this person is a smoker, given that the person develops emphysema, is
(Do not round until the final answer. Then round to four decimal places as needed.)
b) The probability that this person is not a smoker, given that the person does not develop emphysema, is
(Do not round until the final answer. Then round to four decimal places as needed.)
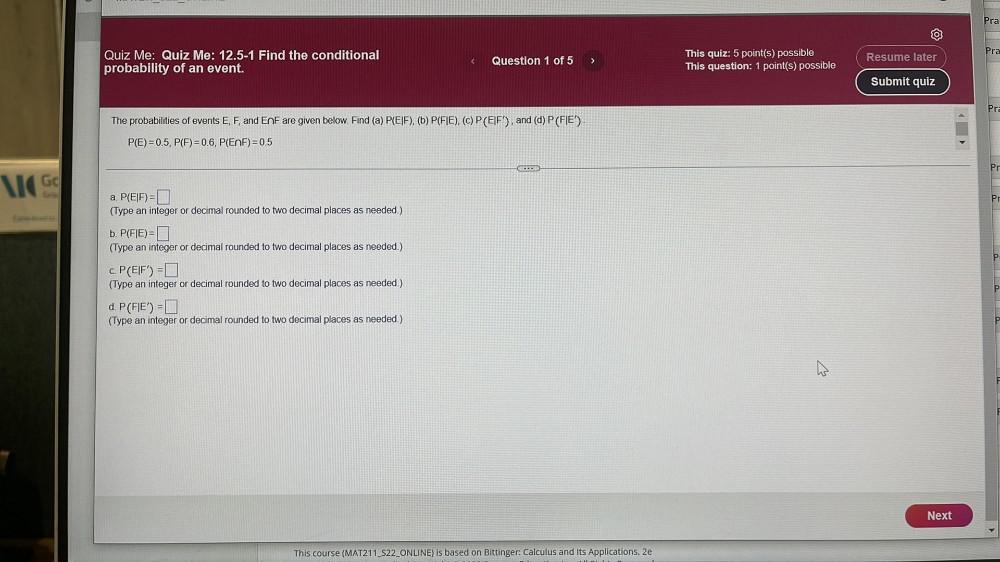
Math
ProbabilityThe probabilities of events E, F, and E⋂F are given below. Find (a) P(EIF), (b) P(FIE), (c) P (EIF'), and (d) P (FIE').
P(E) = 0.5, P(F) = 0.6, P(E⋂F) = 0.5
a. P(EIF) =
(Type an integer or decimal rounded to two decimal places as needed.)
b. P(FIE) =
(Type an integer or decimal rounded to two decimal places as needed.)
c. P (EIF') =
(Type an integer or decimal rounded to two decimal places as needed.)
d. P (FIE') =
(Type an integer or decimal rounded to two decimal places as needed.)
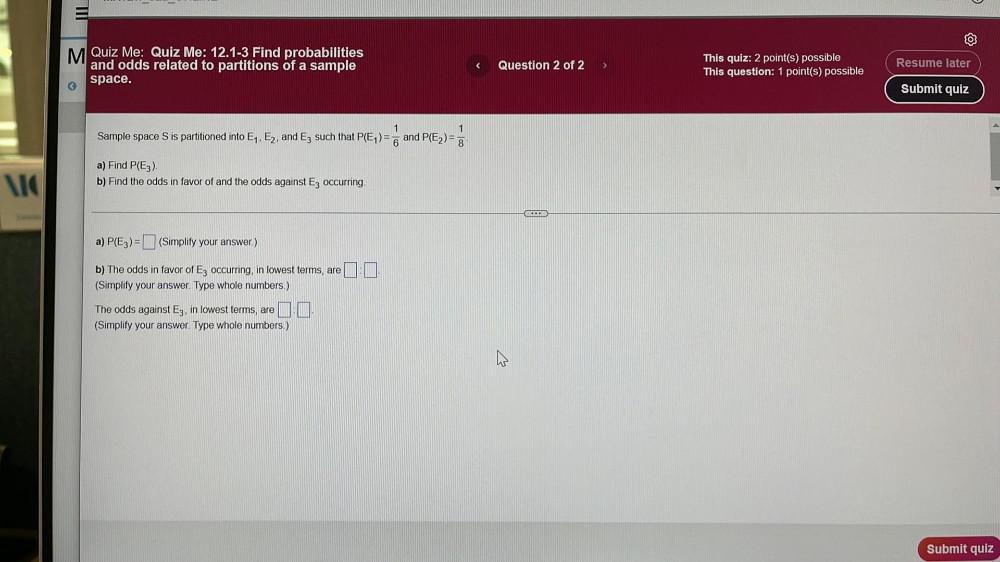
Math
ProbabilitySample space S is partitioned into E₁, E₂, and E₃ such that P(E₁)= 1/6 and P(E₂)= 1/8
a) Find P(E₃).
b) Find the odds in favor of and the odds against E₃ occurring.
a) P(E₃) =
(Simplify your answer.)
b) The odds in favor of E₃ occurring, in lowest terms, are
(Simplify your answer. Type whole numbers.)
The odds against E₃, in lowest terms, are
(Simplify your answer. Type whole numbers.)
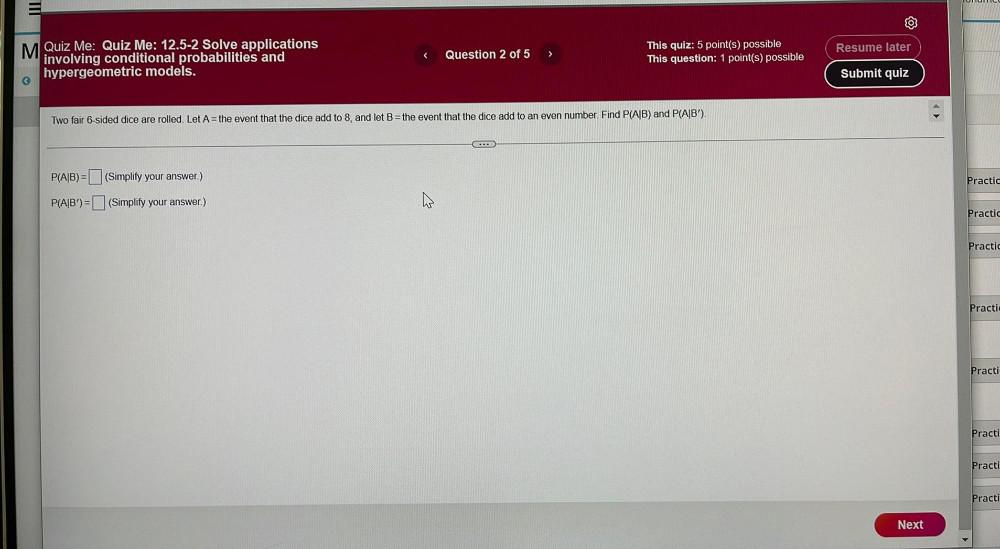
Math
ProbabilityTwo fair 6-sided dice are rolled. Let A = the event that the dice add to 8, and let B = the event that the dice add to an even number. Find P(A|B) and P(A|B').
P(A|B)= (Simplify your answer.)
P(A|B') = (Simplify your answer.)
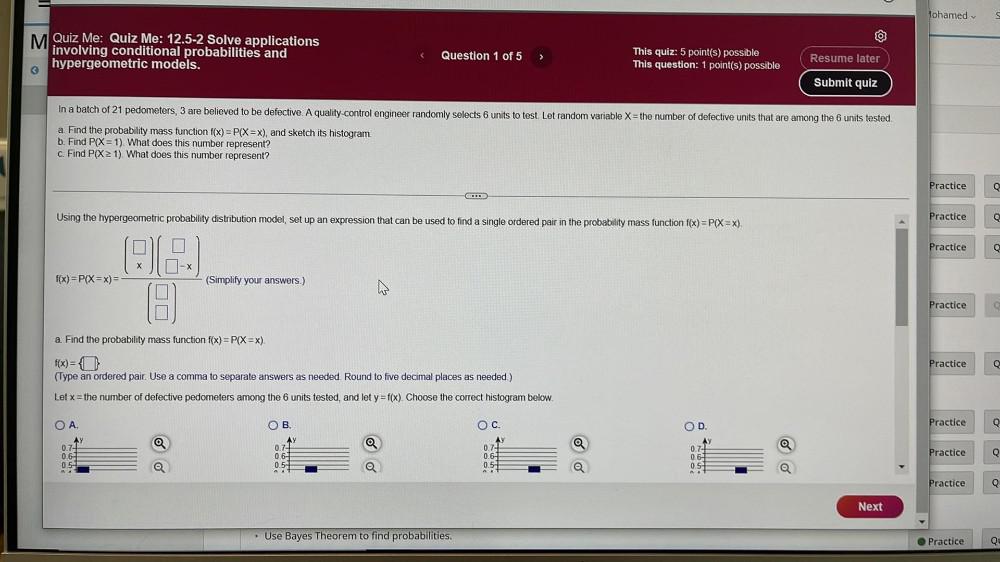
Math
ProbabilityIn a batch of 21 pedometers, 3 are believed to be defective. A quality-control engineer randomly selects 6 units to test. Let random variable X= the number of defective units that are among the 6 units tested.
a. Find the probability mass function f(x)=P(X=x), and sketch its histogram.
b. Find P(X= 1). What does this number represent?
c. Find P(X≥ 1). What does this number represent?
Using the hypergeometric probability distribution model, set up an expression that can be used to find a single ordered pair in the probability mass function f(x)=P(X=x).
f(x)=P(X=x)= (Simplify your answers.)
a. Find the probability mass function f(x)=P(X=x).
f(x) =
(Type an ordered pair. Use a comma to separate answers as needed. Round to five decimal places as needed.)
Let x = the number of defective pedometers among the 6 units tested, and let y=f(x). Choose the correct histogram below.
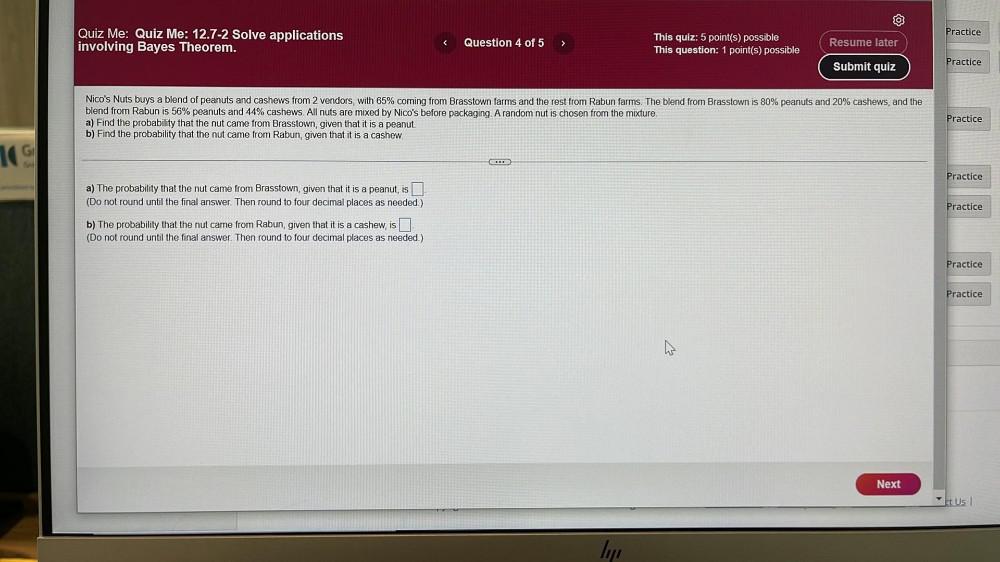
Math
ProbabilityNico's Nuts buys a blend of peanuts and cashews from 2 vendors, with 65% coming from Brasstown farms and the rest from Rabun farms. The blend from Brasstown is 80% peanuts and 20% cashews, and the blend from Rabun is 56% peanuts and 44% cashews. All nuts are mixed by Nico's before packaging. A random nut is chosen from the mixture.
a) Find the probability that the nut came from Brasstown, given that it is a peanut.
b) Find the probability that the nut came from Rabun, given that it is a cashew.
a) The probability that the nut came from Brasstown, given that it is a peanut, is (Do not round until the final answer. Then round to four decimal places as needed.)
b) The probability that the nut came from Rabun, given that it is a cashew, is (Do not round until the final answer. Then round to four decimal places as needed.)
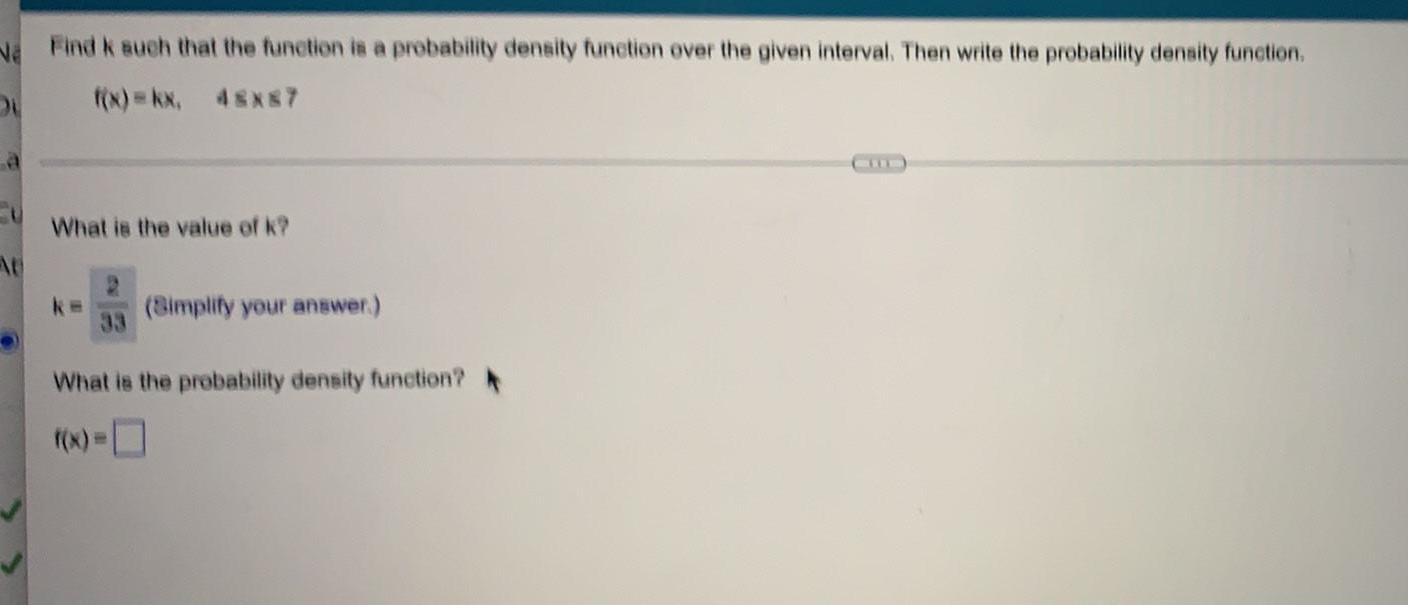
Math
ProbabilityNe Find k such that the function is a probability density function over the given interval. Then write the probability density function.
f(x)=kx, 4≤x≤7
What is the value of k?
k= (Simplify your answer.)
What is the probability density function?
f(x)=

Math
ProbabilityThere is a 25% chance the high school lacrosse team will win its game this week and a 56% chance the high school gymnastics team will win its meet this week. If the events are independent, what is the probability that the lacrosse team and the gymnastics team both win this week?
A 81%
B 52%
C 22%
D 14%

Math
Probability(a) From the 13 albums released by a musician, the recording company wishes to release 10 in a boxed set. How many different boxed sets are possible?
(b) 71 athletes are running a race. A gold medal is to be given to the winner, a silver medal is to be given to the second-place finisher, and a bronze medal is to be given to the third-place finisher. Assume that there are no ties. In how many possible ways can the 3 medals be distributed?

Math
ProbabilityIn one town, 68% of adults have health insurance.
a. What is the probability that 6 adults selected at random from the town all have health insurance?
(Assume the population is large enough that we can consider events to be independent.)
A) 0.68
B) 0.099
C) 0.088
D) 4.08
b. What is the probability that 3 of the 6 adults have health insurance. (use binomial)

Math
ProbabilityA golf ball is selected at random from a golf bag. The golf bag contains the following golf ball brands: 9 Titleists, 8 Maxflis, and 3 Top-Flites. Find the probability that the golf ball is:
A Titleist or Maxfli

Math
ProbabilityOne option in a roulette game is to bet $9 on red. (There are 18 red compartments, 18 black compartments, and two compartments that are neither red nor black.) If the ball lands on red, you get to keep the $9 you paid to play the game and you are awarded $9. If the ball lands elsewhere, you are awarded nothing and the $9 that you bet is collected. Complete parts (a) through (b) below.
a. What is the expected value for playing roulette if you bet $9 on red?
(Round to the nearest cent.)
b. What does this expected value mean? Choose the correct statement below.
A. This value represents the expected loss over the long run for each game played.
B. Over the long run, the player can expect to break even.
C. This value represents the expected win over the long run for each game played.

Math
ProbabilityAn oil company is considering two sites on which to drill. The sites are described in the following table. Complete parts (a) through (b) below.
Site A: Profit if oil is found: $90 million
Site B:Loss if no oil is found: $12 million
Probability of finding oil: 0.2
Profit if oil is found: $135 million
Loss if no oil is found: $25 million
Probability of finding oil: 0.1
a. Which site has the larger expected profit?
Site A has the larger expected profit.
Site B has the larger expected profit.
The expected profits for both sites are the same.
b. If the expected profit for both sites is not the same, by how much is the expected profit larger?
million (Round to the nearest tenth as needed.)

Math
ProbabilityAnswer the question, considering an event to be "unlikely" if its probability is less
than or equal to 0.05.
Is it unlikely to get 11 when a pair of dice is rolled?
Yes
No

Math
ProbabilityThe mathematics department of a college has 14 male professors, 6 female professors, 8 male teaching assistants, and 9 female teaching assistants. If a person is
selected at random from the group, find the probability that the selected person is a teaching assistant or a female.
(Type an integer or a fraction. Simplify your answer.)
The probability is

Math
ProbabilityThe mathematics department of a college has 9 male professors, 9 female professors, 8 male teaching assistants, and 15 female teaching assistants. If a person is
selected at random from the group, find the probability that the selected person is a professor or a male.
(Type an integer or a fraction. Simplify your answer.)
The probability is
Math
ProbabilityLottery: In the New York State Numbers lottery, you pay $2 and can bet that the sum of the numbers that come up is 13. The
probability of winning is 0.08, and if you win, you win $10, which is a profit of $8. If you lose, you lose $2.
Part: 0/2
Part 1 of 2
(a) What is the expected value of your profit? Round the answer to two decimal places.
The expected value of profit is