Probability Questions and Answers

Math
ProbabilitySuppose that E and F are two events and that N(E and F) = 450 and N(E)=810. What is P(FIE)?
Math
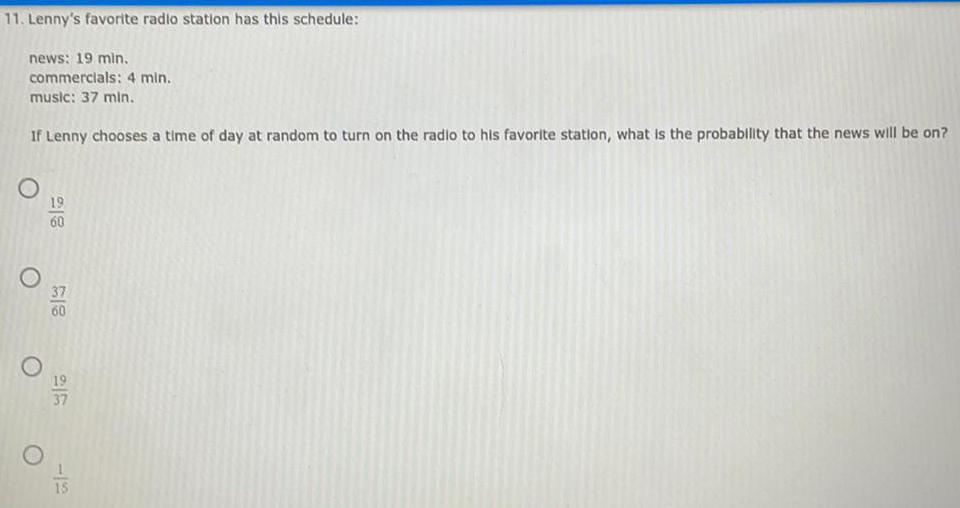
ProbabilityLenny's favorite radio station has this schedule:
news: 19 min.
commercials: 4 min.
music: 37 min.
If Lenny chooses a time of day at random to turn on the radio to his favorite station, what is the probability that the news will be on?
19/60
37/60
19/37
1/15

Math
ProbabilitySuppose you just received a shipment of thirteen televisions. Four of the televisions are defective. If two televisions are randomly selected, compute the probability that
both televisions work. What is the probability at least one of the two televisions does not work?
The probability that both televisions work is.
(Round to three decimal places as needed.)

Math
ProbabilityThere is a traffic light at the intersection of Elm Street and Rose Street. The traffic light on Elm Street follows a cycle. It is green for 20 seconds, yellow for 5 seconds, and red for 25 seconds. As you travel along Elm and approach the intersection, what is the probability that the first color you see is green?
A. 30%
B. 40%
C. 20%
D. 10%

Math
ProbabilityThere is a traffic light at the intersection of Walnut Street and Lawrence Avenue. The traffic light on Walnut Street follows a cycle. It is green for 50 seconds, yellow for 10 seconds, and red for 30 seconds. As you travel along Walnut and approach the intersection, what is the probability that the first color you see is red?
1/3
1/5
1/2
3/5

Math
ProbabilitySuppose a bus arrives at a bus stop every 15 minutes. If you arrive at the bus stop at a random time, what is the probability that you will have to wait at least 10 minutes for the bus?
2/3
1/2
1/3
1/4

Math
ProbabilityAccording to a recent study, 8.5% of high school dropouts are 16-to 17-year-olds. In addition, 6.3% of high school dropouts are white 16-to 17-year-olds. What is the probability that a randomly selected dropout is white, given that he or she is 16 to 17 years old?

Math
ProbabilityOak Street intersects with Mill Avenue. The traffic light on Oak Street follows a cycle. It is green for 35 seconds, yellow for 5 seconds, and red for 20 seconds. As you travel along Oak and approach the intersection, what is the probability that the first color you see is red? Write the probability as a simplified fraction.

Math
ProbabilityA bag contains four red marbles, three blue marbles, and three yellow marbles. You randomly pick three marbles without replacement. The first marble is red, the second marble is blue, and the third marble is red.
Find the probability of this occuring.
A. 25/546
B. 1/96
C. 1/20
D. 1/256

Math
ProbabilityUse permutations and/or combinations to calculate the probability of getting 3 diamonds and a heart from picking 4 cards from a deck of 52 (assume 4 suites of 13).Verify your answer using fractional probability.

Math
ProbabilitySuppose you have a bag of 10 marbles that includes 4 red marbles. Create a table that shows the theoretical probability distribution of how many reds you could choose if you take out 2 marbles.

Math
ProbabilitySelect the correct answer from each drop-down menu.
Of the 16 cards drawn from a standard deck of 52 cards, experimental probability of drawing a spade is a spade from a standard deck of cards is 5 of the cards are spades. Based on the cards that were drawn, the and the difference of the experimental and theoretical probabilities of drawing a spade from a standard deck of cards is____

Math
ProbabilityAssume that the weights of ripe watermelons grown at a particular farm are normally distributed with a mean of 90 pounds and a standard deviation of 1.9 pounds. Determine the percent of watermelons that weigh between 88.15 pounds and 92.45 pounds.

Math
ProbabilityFill in the blank with an appropriate word or phrase.
A listing of observed values and the corresponding frequency of occurrence of each value is called a distribution.

Math
ProbabilityThe mathematics department of a college has 8 male professors, 12 female professors, 12 male teaching assistants, and 12 female teaching assistants. If a person is selected at random from the group, find the probability that the selected person is a teaching assistant or a female.

Math
ProbabilityBubba Watson led the PGA tour in driving distance during the 2015 season. The length of his
drives followed a normal distribution with a mean of 317 yards and a standard deviation of 10
yards. Find the percent of his drives that you would expect to have been:
a) greater than 300 yards
b) less than than 305 yards
c) between 320 and 330 yards

Math
ProbabilityThree letters are to be selected at random from the English alphabet of 26 letters. Determine the probability that 3 consonants are selected. Assume there are 21
consonants in the alphabet and that selection is to be done without replacement.
Set up the problem as if it were to be solved, but do not solve.
P(3 consonants selected) =
Math
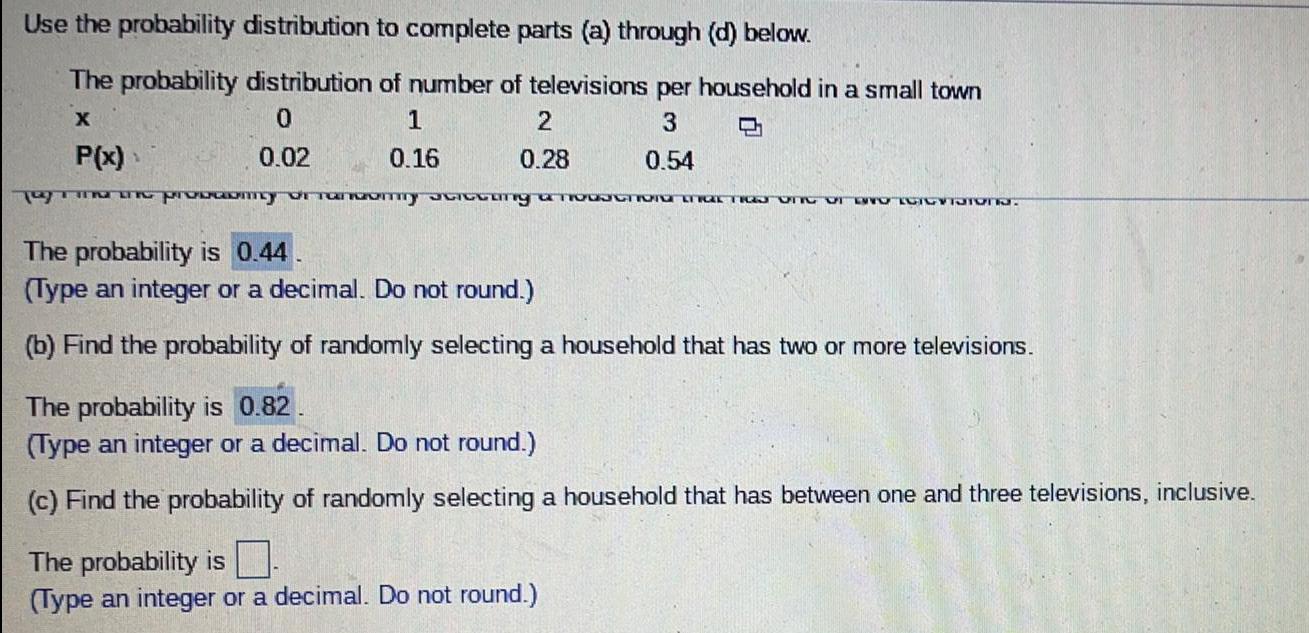
ProbabilityUse the probability distribution to complete parts (a) through (d) below.
The probability distribution of number of televisions per household in a small town
The probability is
(Type an integer or a decimal. Do not round.)
(b) Find the probability of randomly selecting a household that has two or more televisions.
The probability is
(Type an integer or a decimal. Do not round.)
(c) Find the probability of randomly selecting a household that has between one and three televisions, inclusive.
The probability is
(Type an integer or a decimal. Do not round.)

Math
ProbabilityAssume that the probability of any newborn baby being a boy is1/2 and that all births are independent. If a family has three children (no twins), what is the probability of the event that none of them are boys? The probability is (Simplify your answer.)

Math
ProbabilityTen red balls and three blue balls are in a bag. If two balls from the bag are to be selected at random, determine the probability of selecting two red balls. Assume that selection is to be done without replacement.
Set up the problem as if it were to be solved, but do not solve.
P(2 red balls selected) =

Math
ProbabilityThe numbers 1-10 are written on
pieces of paper and put into a hat.
What is the probability of drawing
an even number, and then another
even number, without replacing
the first number?

Math
ProbabilityAt a school there are 10 students taking only
Chemistry, 9 students taking only Physics,
5 students taking both, and 16 students not
taking either. If a student is randomly selected
from the school, what is the probability that
they are taking Chemistry or Physics?

Math
ProbabilityThis probability distribution shows the
typical distribution of the number of shoes
in a teenager's closet.
Using this distribution, find the probability
that a teenager has 4 or more pairs of shoes
in their closet.

Math
ProbabilityAssume the annual salaries of police officers are normally distributed with a mean of $41,000 and a standard deviation of $2000. Determine the percent of police officers with an annual
salary of at least $41,000.



Math
ProbabilityTwenty out of every fifty CDs
produced in a factory are
scratched. What is the ratio of
unscratched to scratched CDs?
Enter a, b, c, d, or e.
a. 2:5
b. 3:5
c. 2:3
d. 3:2
e. 5:2

Math
ProbabilityTwo dice are rolled.
What is the probability that both die will show even numbers?
Give your answer as a decimal.

Math
ProbabilityIf the wheel is spun and each section is equally likely to stop under the pointer, determine the probability that the pointer lands on a number greater than 1, given that the color is red or purple. Note that the red sectors are the sectors numbered 5, 6, and 7, and the purple sectors are numbered 2, 4, 9, 11, and 12.
What is the probability?
(Type an integer or a simplified fraction.)

Math
ProbabilityA bag contains 2 green marbles, 4 red marbles, and 3 blue marbles. 3 marbles are drawn from the bag without replacement. Find the probability of drawing 2 red marbles and 1 blue marble. Express your answer as a reduced fraction.
3/14
108/504
1/14
36/504

Math
ProbabilityA card is drawn at random from a standard deck of playing cards (no jokers). If it is black, the player wins 1 dollar; if it is not black, the player loses 4 dollars. Find the expected value of the game.

Math
ProbabilityA card is drawn from a standard, well-shuffled deck of 52 cards. What is the probability that it is a face card (J, Q, or K)?

Math
ProbabilityIn a class there are 14 students: 4 are 5' 6", 2 are 5'8", 2 are 5'10", 3 are 6', and 3 are 6' 2". A student is chosen at random. What is the student's expected height in inches? Round to the nearest tenth of an inch.

Math
ProbabilityYou own 22 CDs. You want to randomly arrange 9 of them in a CD rack. What is the probability that the rack ends up in alphabetical order? The probability that the CDs are in alphabetical order is

Math
ProbabilityIn a lottery game, a player picks six numbers from 1 to 20. If the player matches all six numbers, they win 50,000 dollars. Otherwise, they lose $1.

Math
ProbabilityIf you pull a card from a well shuffled deck, what is the probability that you get a club or a red card?
Enter your answer as a fraction

Math
ProbabilityIn a large population, 54 % of the people have been vaccinated. If 4 people are randomly selected,
what is the probability that AT LEAST ONE of them has been vaccinated?
Give your answer as a decimal (to at least 3 places) or fraction.

Math
ProbabilityA card is picked from a standard deck of 52 cards. Determine the odds against and the odds in favor of selecting a black face card (king, queen, or jack).
The odds against selecting a black face card are:0
The odds in favor of selecting a black face card are

Math
ProbabilityAccording to a study, 84% of K-12 schools or districts in a country use digital content such as ebooks, audio books, and digital textbooks. Of these 84%, 13 out of 20 use digital content as part of their curriculum. Find the probability that a randomly selected school or district uses digital content and uses it as part of their curriculum.
Math
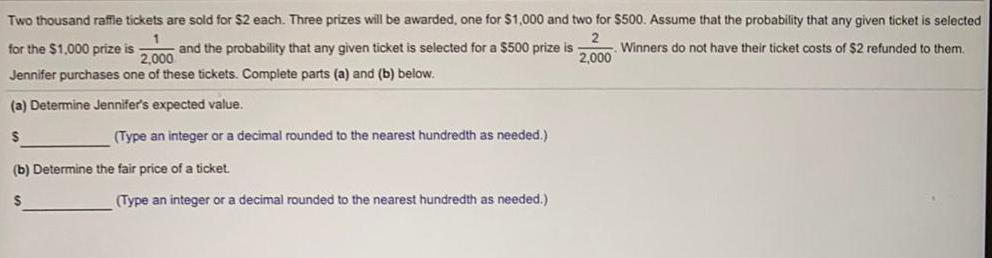
ProbabilityTwo thousand raffle tickets are sold for $2 each. Three prizes will be awarded, one for $1,000 and two for $500. Assume that the probability that any given ticket is selected 1 for the $1,000 prize is and the probability that any given ticket is selected for a $500 prize is 1/2,000 Jennifer purchases one of these tickets. Complete parts (a) and (b) below. 2/2,000 Winners do not have their ticket costs of $2 refunded to them.
(a) Determine Jennifer's expected value. (Type an integer or a decimal rounded to the nearest hundredth as needed.).
(b) Determine the fair price of a ticket. (Type an integer or a decimal rounded to the nearest hundredth as needed.)

Math
ProbabilityThe owner of an antique store estimates that there is a 40% chance she will make $2400 when she sells an antique china cabinet, a 15% chance she will make $1500 when she sells the cabinet, and a 45% chance she will break even when she sells the cabinet. Determine the expected gain or loss for the store.
Math
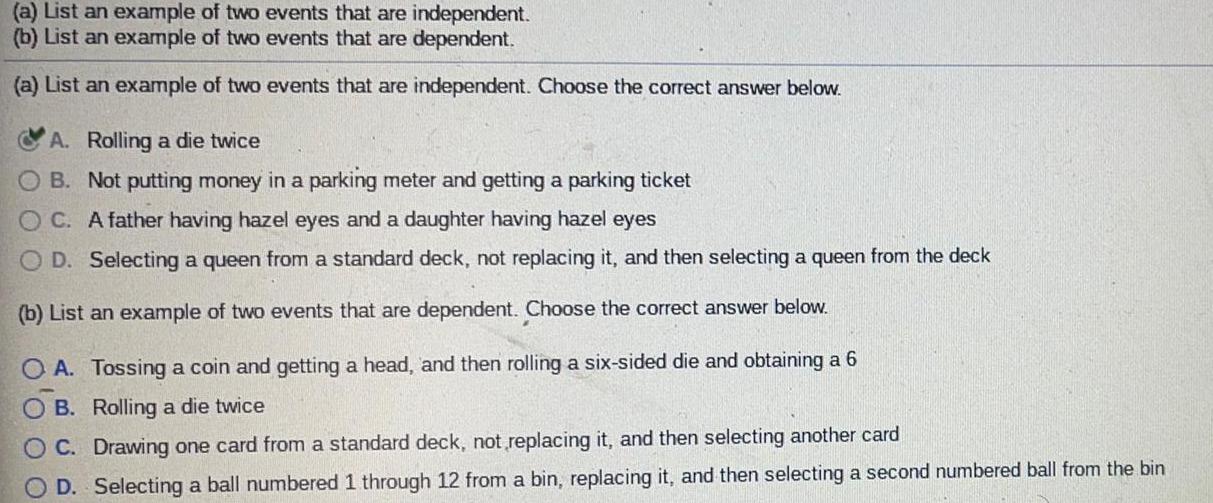
Probability(a) List an example of two events that are independent.
(b) List an example of two events that are dependent.
(a) List an example of two events that are independent. Choose the correct answer below.
A. Rolling a die twice
B. Not putting money in a parking meter and getting a parking ticket
C. A father having hazel eyes and a daughter having hazel eyes
D. Selecting a queen from a standard deck, not replacing it, and then selecting a queen from the deck
(b) List an example of two events that are dependent. Choose the correct answer below.
A. Tossing a coin and getting a head, and then rolling a six-sided die and obtaining a 6
B. Rolling a die twice
C. Drawing one card from a standard deck, not replacing it, and then selecting another card
D. Selecting a ball numbered 1 through 12 from a bin, replacing it, and then selecting a second numbered ball from the bin

Math
ProbabilitySuppose you reach into your mailbox that contains 8 pieces of junk mail, 4 letters, and 1 magazine. Assuming you can't feel the difference between the types of mail, what is the probability that you select either a letter or the magazine? Enter your answer as a fraction.

Math
ProbabilityBased on his past baseball history, Kurt has a(n) 16% chance of reaching first base safely, a(n) 8% chance of hitting a double, a(n) 5% chance of hitting a triple, a(n) 5% chance of hitting a home run, and a(n) 66% chance of making an out at his next at bat. Determine Kurt's expected number of bases for his next at bat.

Math
ProbabilitySuppose that 52% of students in a college have a smart phone. If you select three students at random, what is the probability that all three have a smart phone?

Math
ProbabilityConsider a collection of envelopes consisting of 1 red envelope, 2 blue envelopes, 2 green envelopes, and 3 yellow envelopes. If two envelopes are selected at random, with replacement, determine the probability that both are blue envelopes.

Math
ProbabilityNatasha buys a bag of cookies that contains 8 chocolate chip cookies, 9 peanut butter cookies, 5 sugar cookies and 9 oatmeal raisin cookies. What is the probability that Natasha randomly selects a chocolate chip cookie from the bag, eats it, then randomly selects another chocolate chip cookie? Express your answer as a reduced fraction.
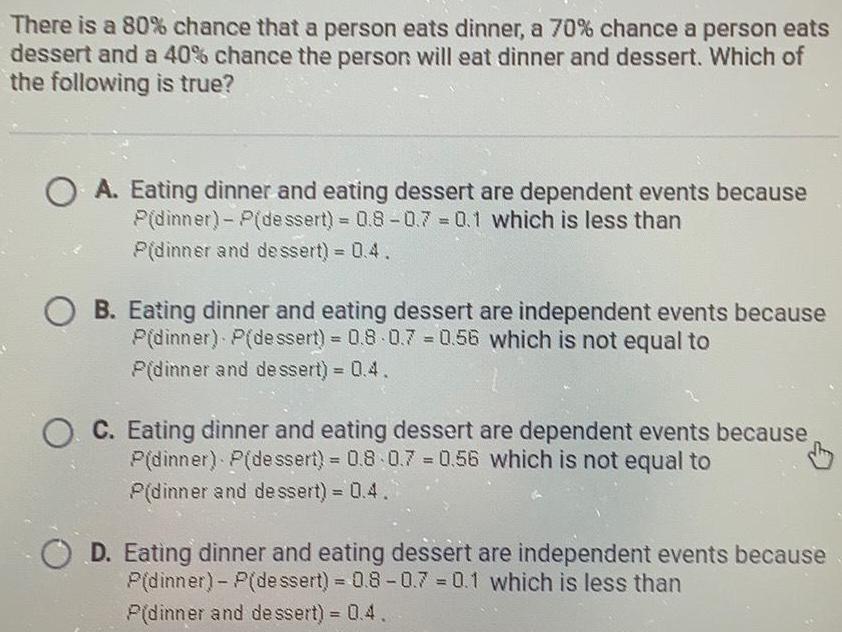
Math
ProbabilityThere is a 80% chance that a person eats dinner, a 70% chance a person eats dessert and a 40% chance the person will eat dinner and dessert. Which of the following is true?
A. Eating dinner and eating dessert are dependent events because P(dinner) - P(dessert) = 0.8 -0.7 = 0.1 which is less than P(dinner and dessert) = 0.4.
B. Eating dinner and eating dessert are independent events because P(dinner) P(dessert) = 0.8.0.7 = 0.56 which is not equal to P(dinner and dessert) = 0.4.
C. Eating dinner and eating dessert are dependent events because P(dinner) P(dessert) = 0.8 0.7 = 0.56 which is not equal to P(dinner and dessert) = 0.4.
D. Eating dinner and eating dessert are independent events because P(dinner) - P(dessert) = 0.8 -0.7 = 0.1 which is less than P(dinner and dessert) = 0.4.

Math
ProbabilityA bag of M&M's has 3 red, 6 green, 5 blue, and 2 yellow M&M's. What is the probability of randomly
picking:
(give answer as a reduced fraction)
1) a yellow?
2) a blue or green?
3) an orange?

Math
ProbabilityOf the last 60 people who went to the cash register at a department store, 14 had blond hair, 17 had black hair, 24 had brown hair, and 5 had red hair. Determine the empirical probability that the next person to come to the cash register has blond hair.