Sequences & Series Questions and Answers

Math
Sequences & Series300 people are lined up outside of Disneyland, and all enter by 8:15 am. By 8:30 am, 550 more people enter, and every 15 minutes afterwards, the number of people who enter increases by 250. All of these people are planning to stay for the Marvel parade at noon.
a. Represent this problem as a sequence and write a formula for the nth term.
b. How many people will enter the park between 11:45 and noon?
Math
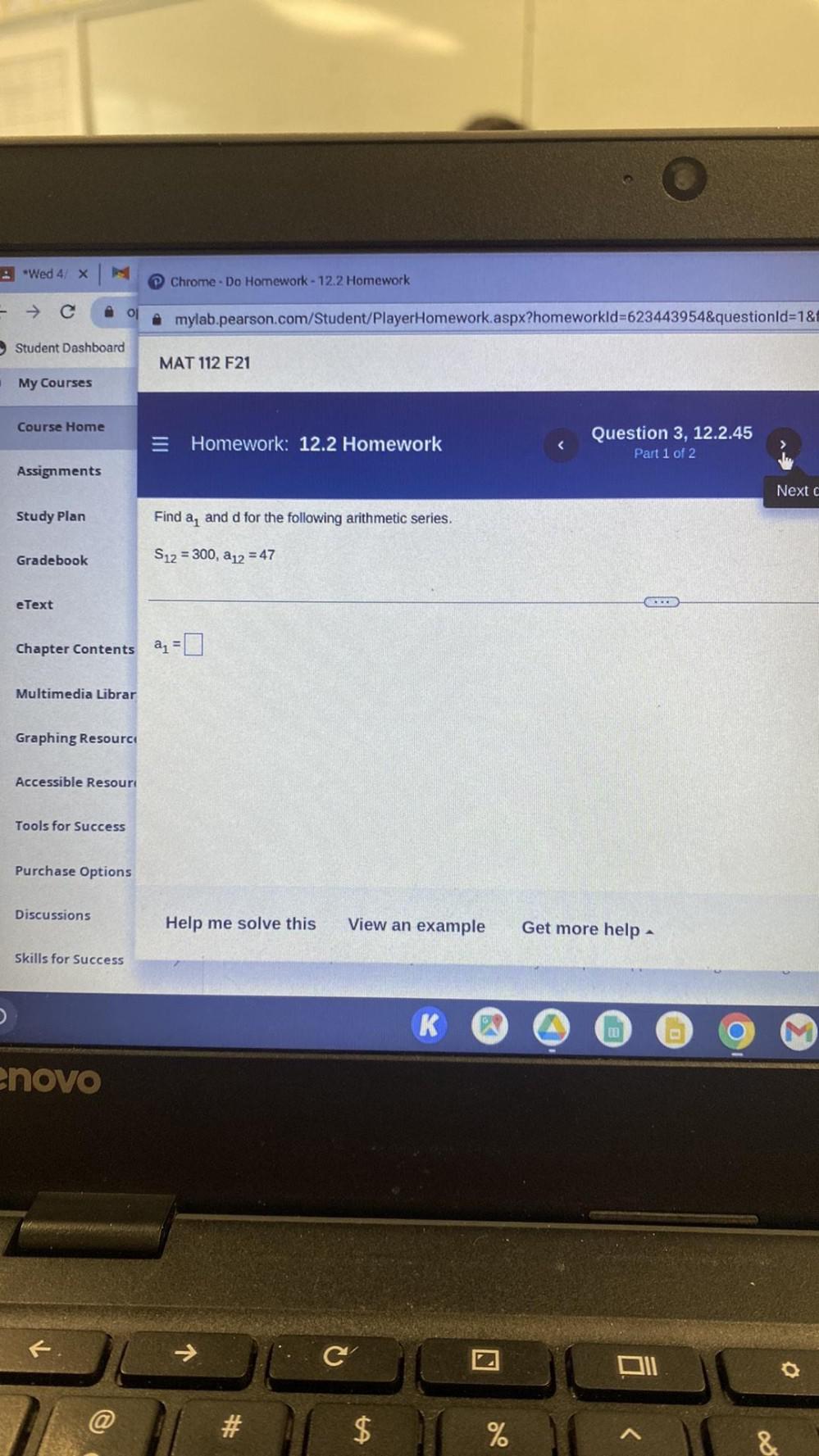
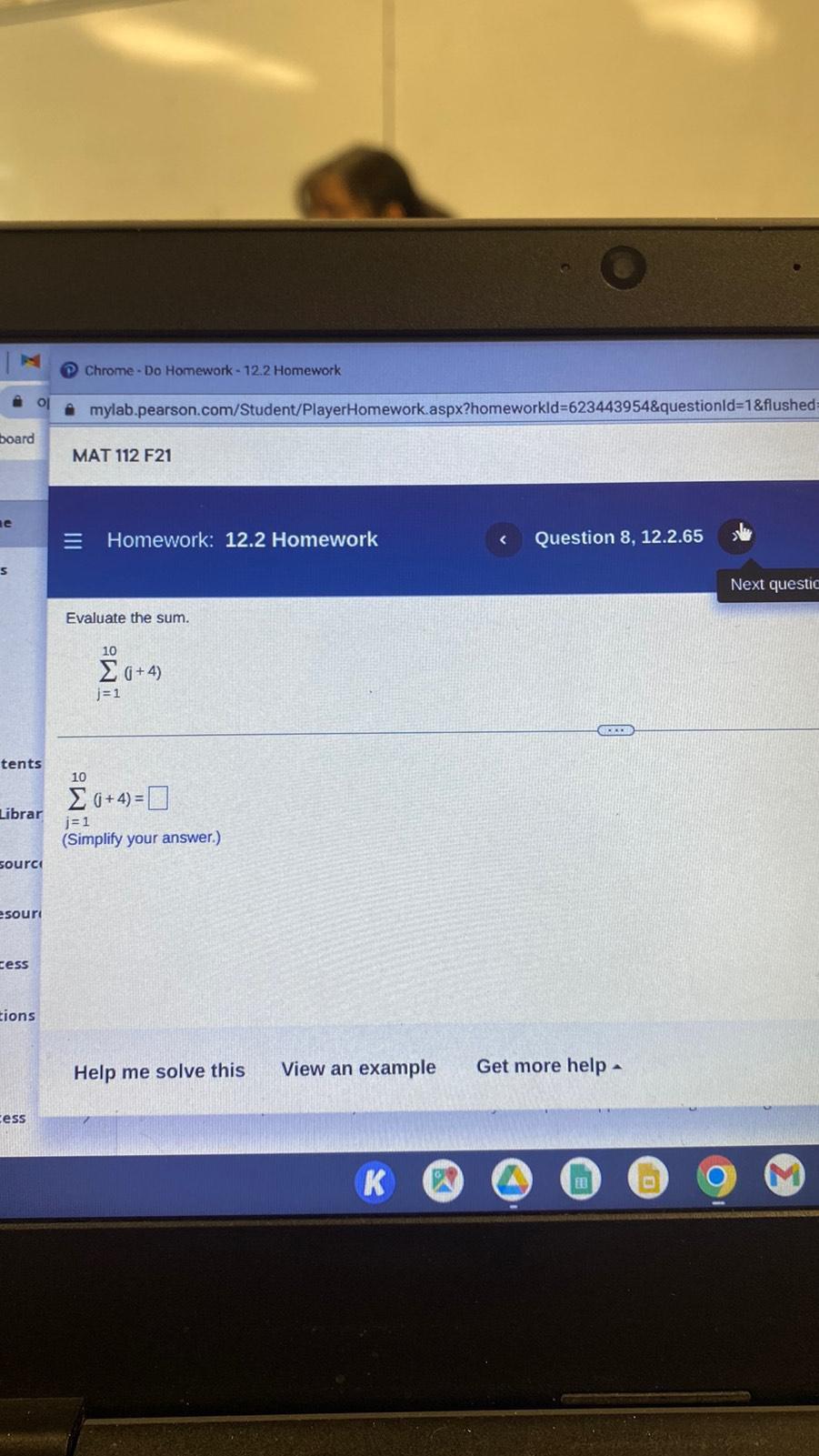
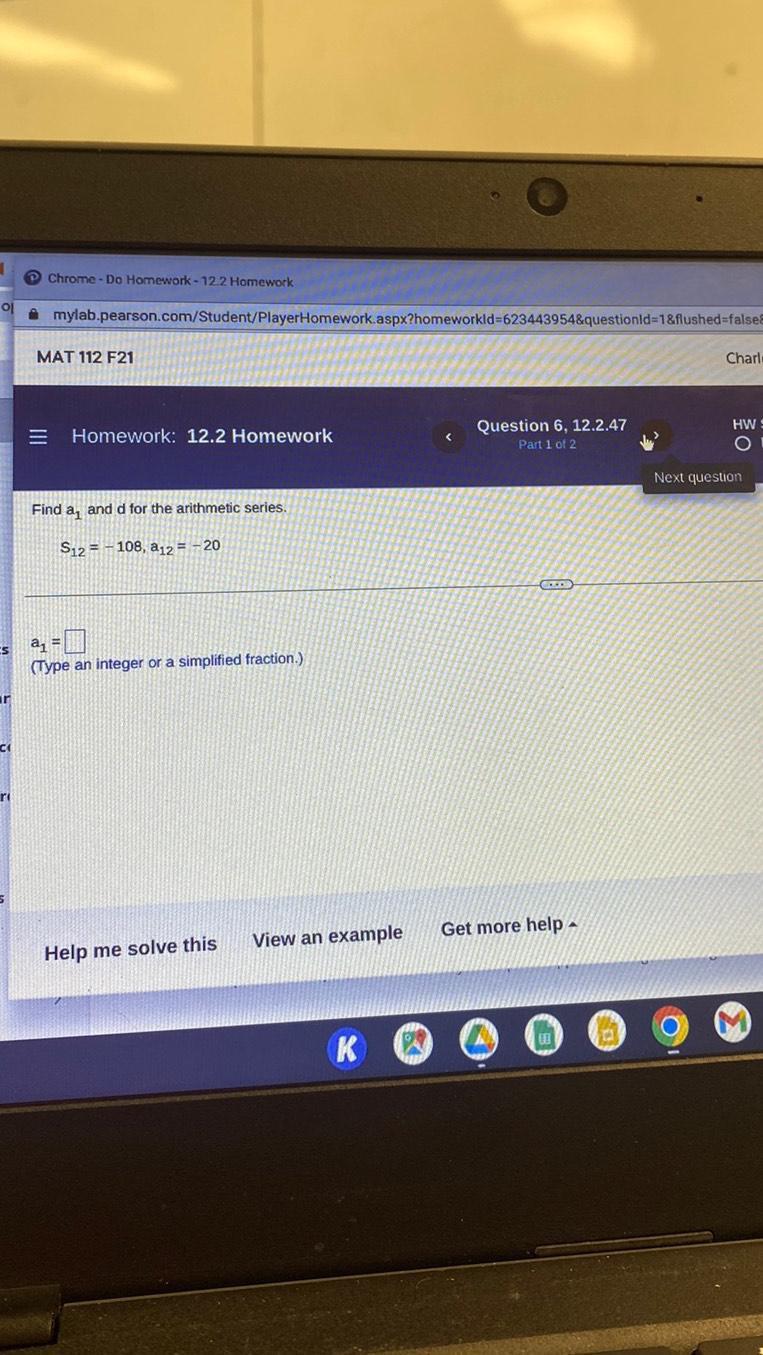
Sequences & SeriesFind a1 and d for the following arithmetic series.
S12 = 300, a12 = 47
a1 = ____.
Math
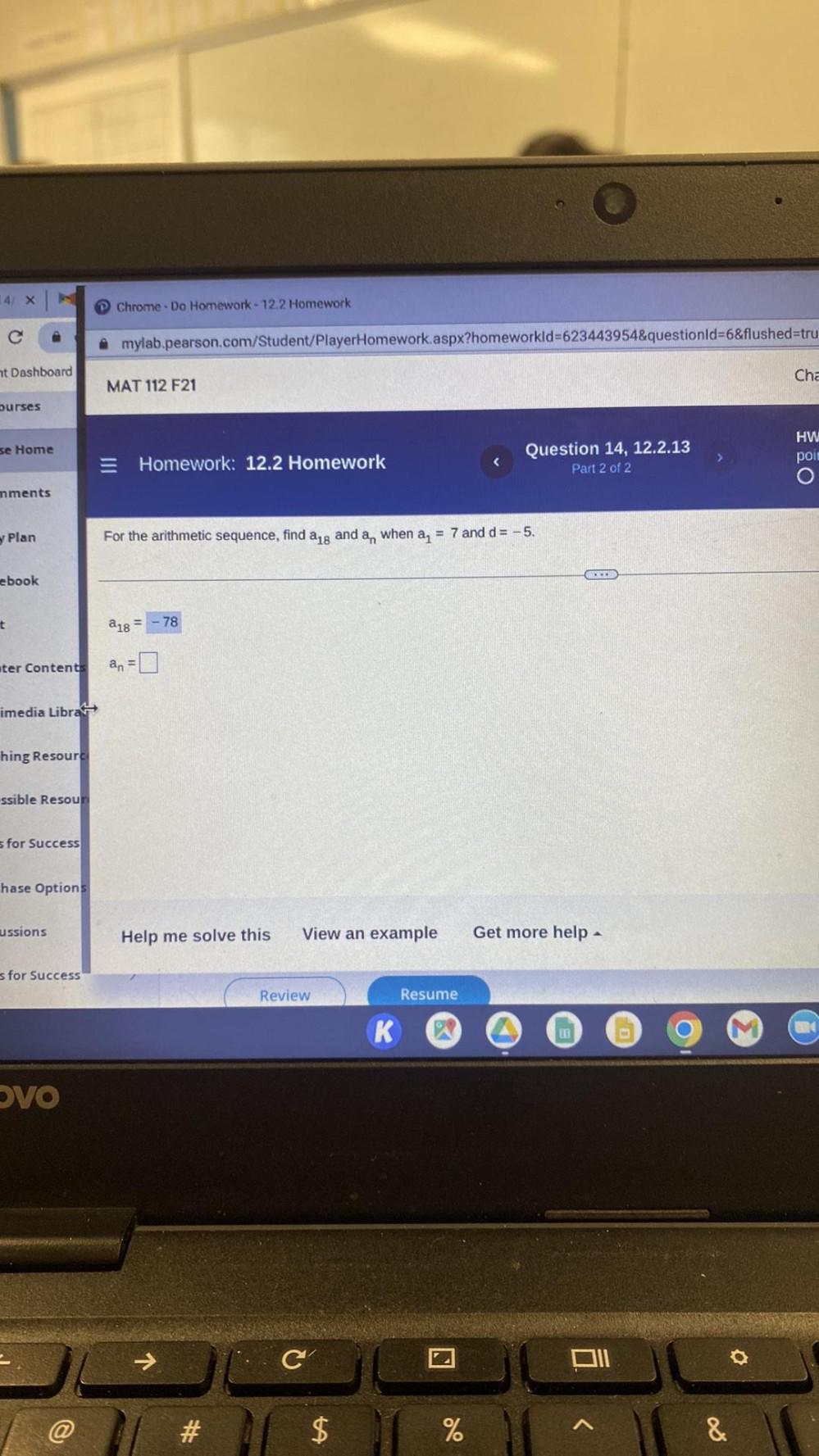
Sequences & SeriesFor the arithmetic sequence, find a18 and an when a1 = 7 and d = -5.
a18 = -78.
an = ____.

Math
Sequences & SeriesThe median home value in Georgia and Colorado (adjusted for inflation) are shown below.
Year Georgia Colorado
1950 31700 43300
2000 111200 166600
If we assume that the house values are changing linearly,
a) In which state have home values increased at a higher rate?
b) If these trends were to continue, what would be the median home value in Georgia in 2010?
Math
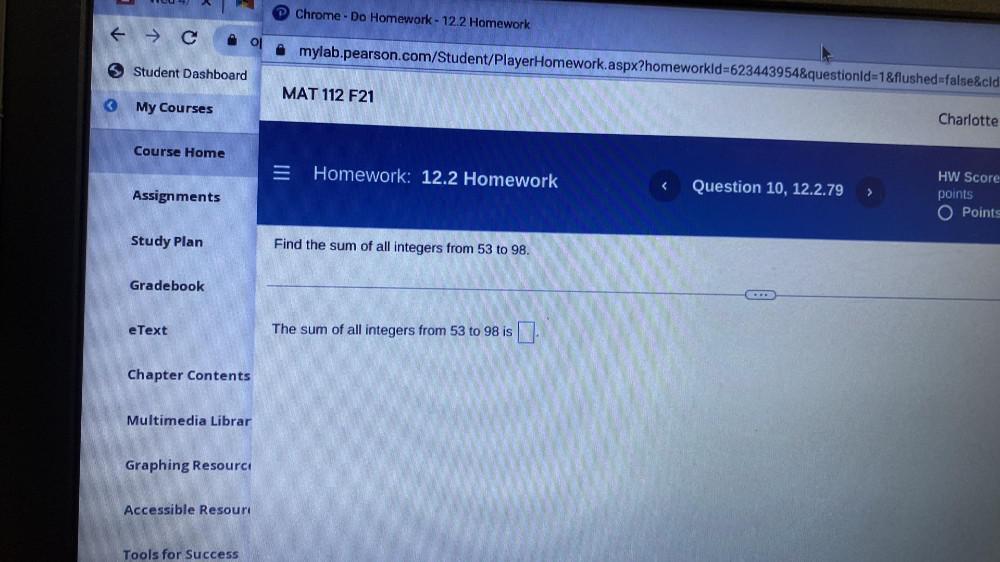
Sequences & SeriesFind the sum of all integers from 53 to 98.
The sum of all integers from 53 to 98 is ______________.
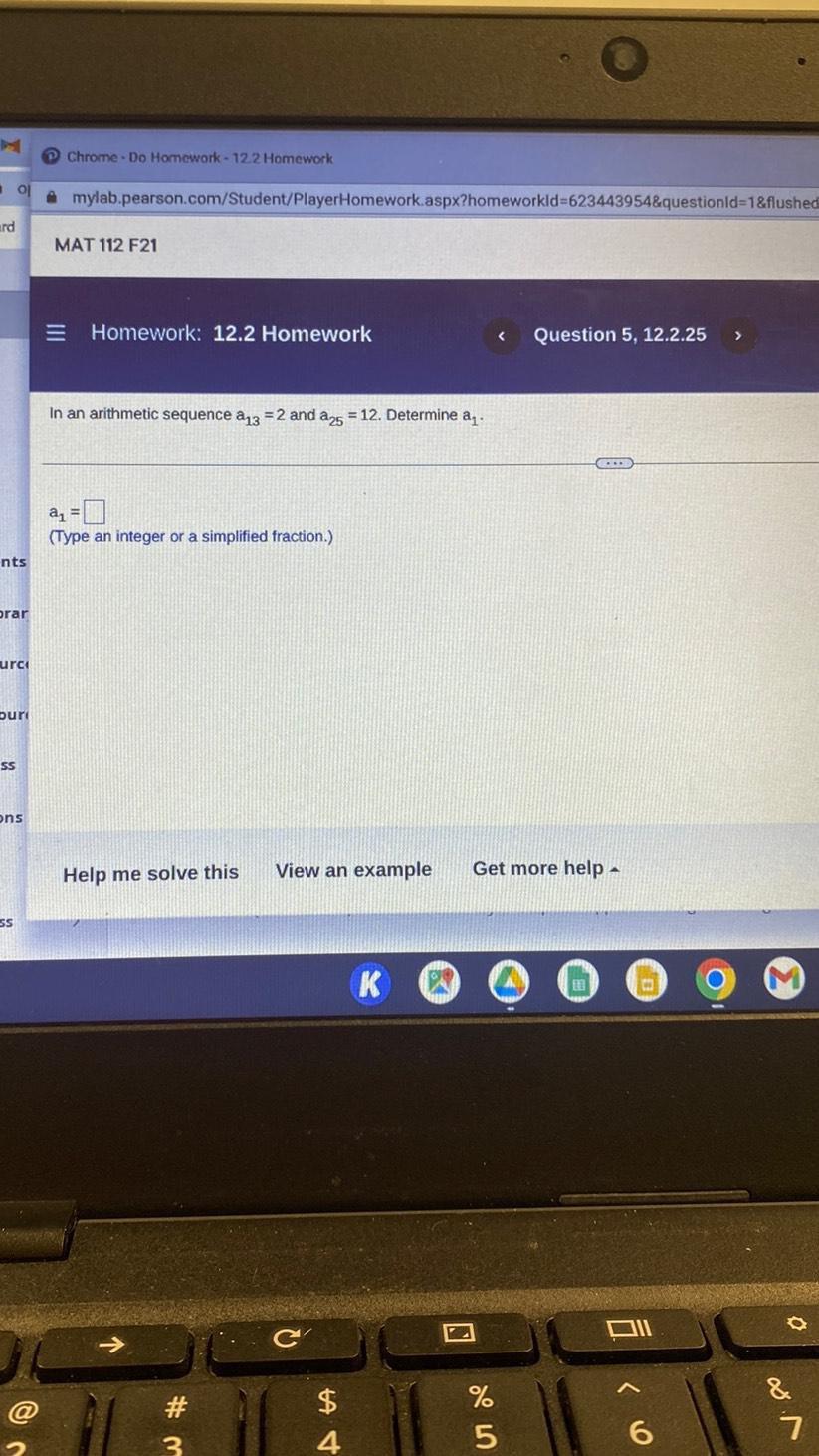
Math
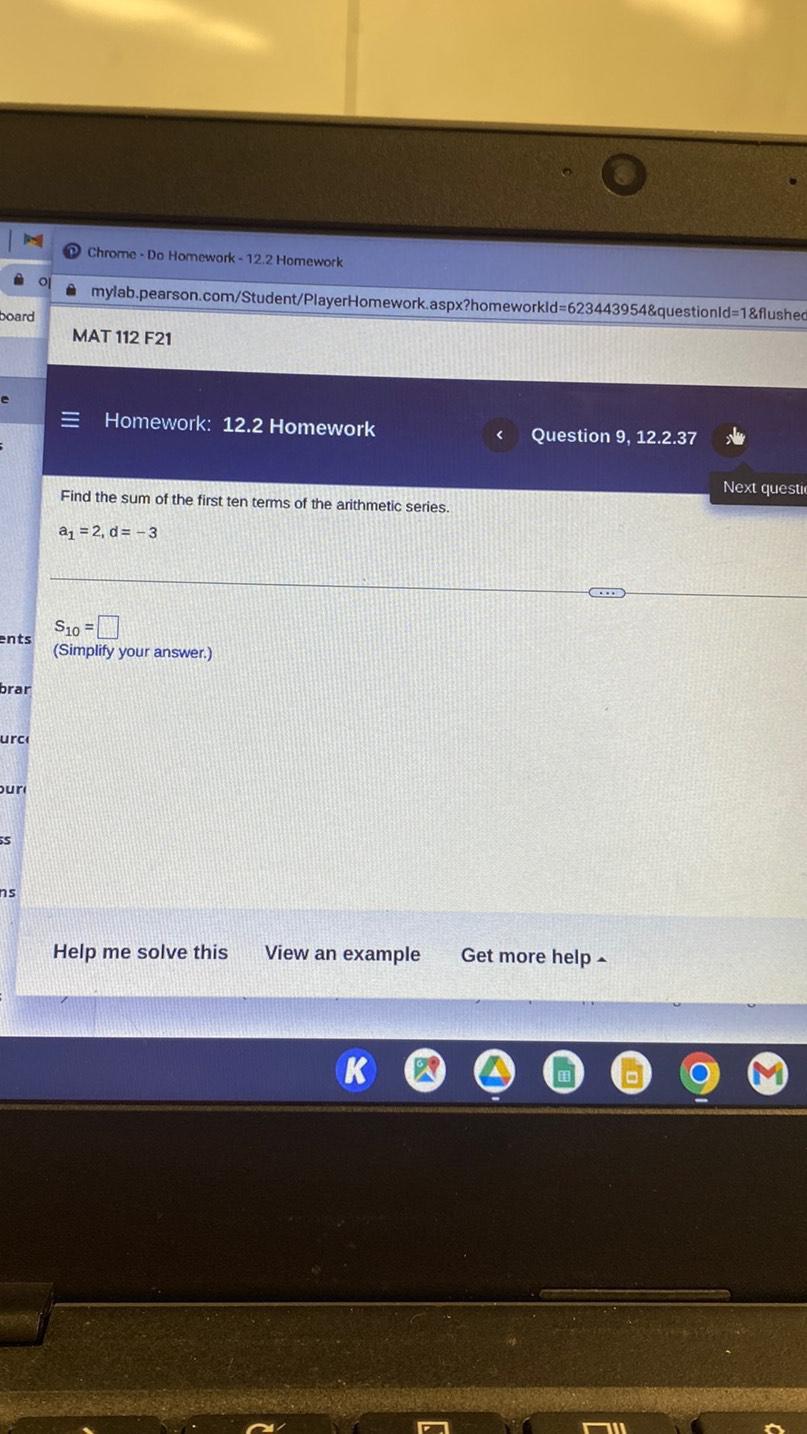
Sequences & SeriesFind the sum of the first ten terms of the arithmetic series.
a1 = 2, d = -3
S10 = ______.


Math
Sequences & SeriesUse the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence with the given first term, a1 and common difference, d.
Find a250 when a₁ = -60, d = 5.

Math
Sequences & SeriesWrite a formula for the general term (the nth term) of the arithmetic sequence shown below. Do not use a recursion formula. Then use the formula for an to find a20. the 20th term of the sequence.
an = an-1 - 10, a1 =32


Math
Sequences & SeriesUse the formula for the general term (the nth term) of a geometric sequence to find the indicated term of the following sequence with the given first term, a₁, and common ratio, r.
Find a6 when a₁ = 8 and r=3.

Math
Sequences & SeriesWrite the first six terms of the following arithmetic sequence.
an= a(n-1)-0.3, a₁ = 0.9

Math
Sequences & SeriesWrite the first six terms of the arithmetic sequence shown below.
an = a(n-1) +9, a₁ = -7
Math
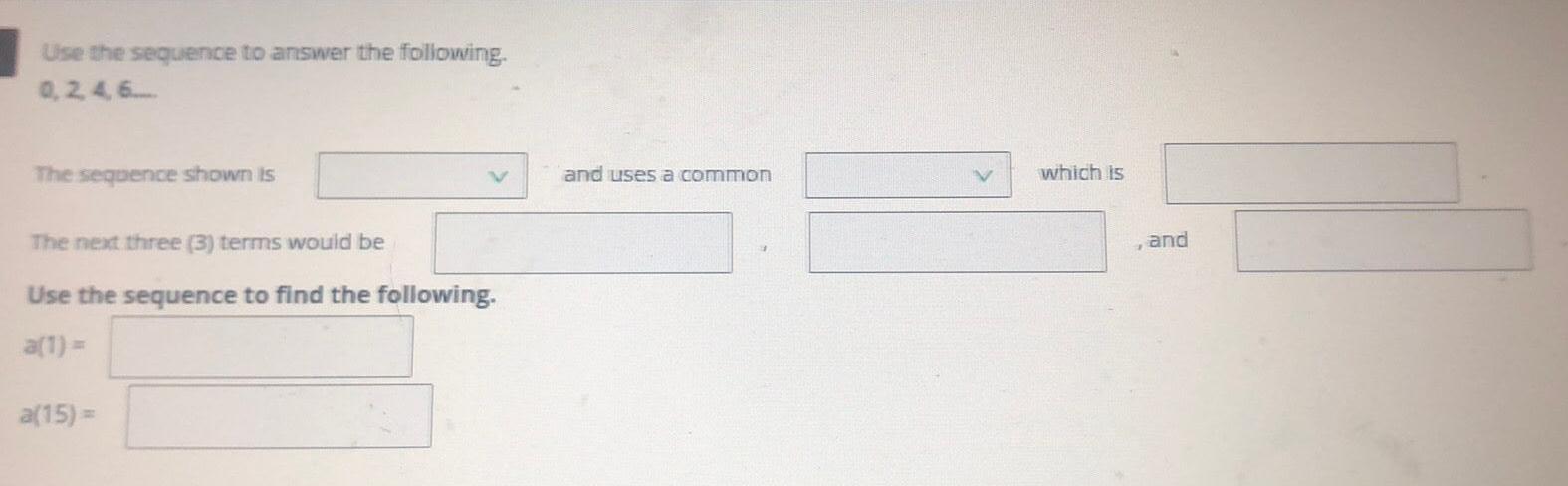
Sequences & SeriesUse the sequence to answer the following.
0, 2, 4, 6,.......
The sequence shown is___and uses a common___which is___
The next three (3) terms would be___,____, and___
Use the sequence to find the following.
a(1) =
a(15) =

Math
Sequences & SeriesFind the 9th term of the given geometric sequence:
1, 3, 9, 27....
A) 6561
B) 271
C) 19683
D 243

Math
Sequences & SeriesWhat is the explicit rule for the geometric sequence 3, 12, 48,...?
A) f(n)= 9n-1
B) f(n) = 4(3)n-1
c) f(n) = 3(4)n-1
D) f(n) = 4n-1 +3
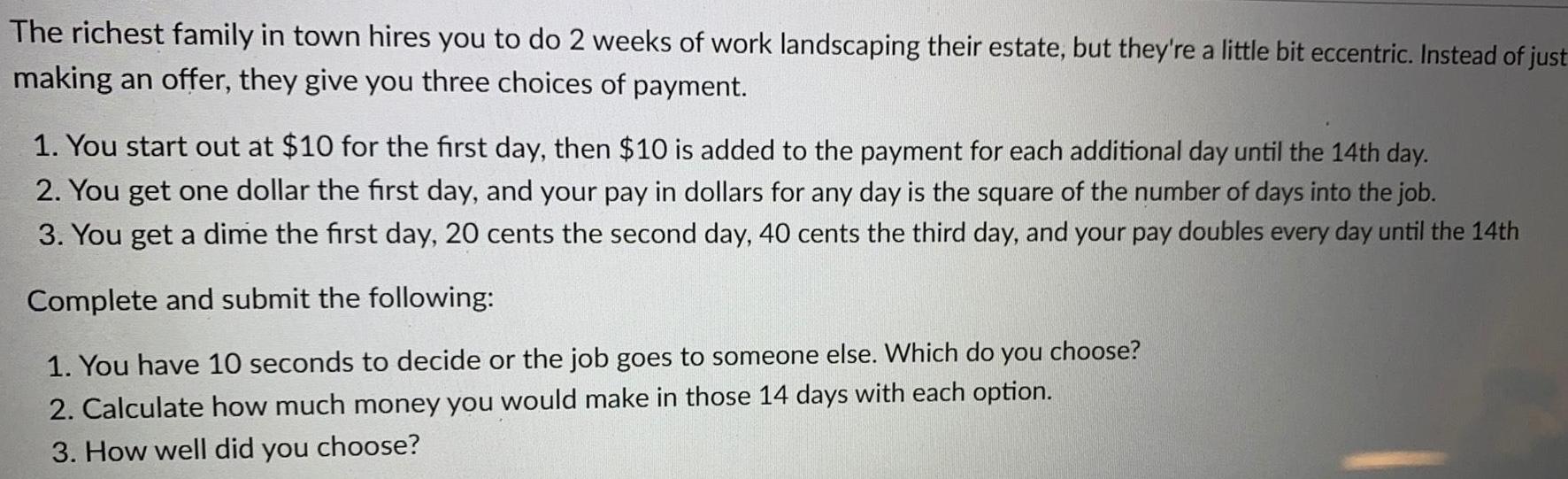
Math
Sequences & SeriesThe richest family in town hires you to do 2 weeks of work landscaping their estate, but they're a little bit eccentric. Instead of just
making an offer, they give you three choices of payment.
1. You start out at $10 for the first day, then $10 is added to the payment for each additional day until the 14th day.
2. You get one dollar the first day, and your pay in dollars for any day is the square of the number of days into the job.
3. You get a dime the first day, 20 cents the second day, 40 cents the third day, and your pay doubles every day until the 14th
Complete and submit the following:
1. You have 10 seconds to decide or the job goes to someone else. Which do you choose?
2. Calculate how much money you would make in those 14 days with each option.
3. How well did you choose?

Math
Sequences & SeriesThe numerator and denominator of a fraction are in the ratio of 3 to 5. If the numerator and denominator are both decreased by 2, the fraction is now equal to 1/2.
If n = the numerator and d = the denominator, which of the following systems of equations could be used to solve the problem?
3n = 5d and 2n-4-d-2
5n = 3d and n -2=2d-4
5n 3d and 2n-4d-2


Math
Sequences & SeriesAn arithmetic sequence is one that involves adding or subtracting by the same number to each term in the sequence.
A geometric sequence is one that involves multiplying or dividing by the same number to each term in the sequence.
Classify each sequence as arithmetic, geometric, or neither. There should be two sequences in each category.


Math
Sequences & SeriesFind the thirty-second term of the following sequence.
9, 15, 21, ...
199
195
186

Math
Sequences & SeriesA homeowner purchases a riding lawn mower for $3600. Its value is expected to depreciate (decrease) by $400 each year. How many years will it take for the lawn mower to lose all its value (that is, have a value of $0)?

Math
Sequences & SeriesThis month a city has 50 street lights installed. Next
month it plans to have 54 lights installed, and 58 the
following month. If this rate of change continues each
month, what is the value of d (the growth factor) in the
explicit linear growth equation that models this?
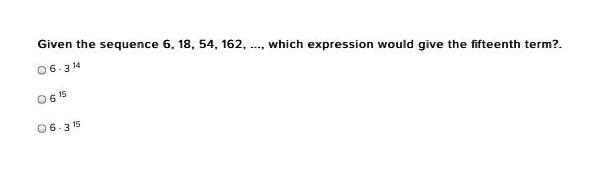
Math
Sequences & SeriesGiven the sequence 6, 18, 54, 162, ..., which expression would give the fifteenth term?.
6.314
6
15
6.315

Math
Sequences & SeriesA city presently has 2800 water meters installed (business and residential). The planning board estimates that an average of 30 new ones will be installed each month. How many water meters will there be at the end of a year?

Math
Sequences & SeriesFind the 30th term of the following sequence.
1, 7, 13, 19, ...
180
174
175
181

Math
Sequences & SeriesGiven the following geometric sequence, find the common ratio.
(0.45, 0.9, 1.8,...)
2
0.45
0.9
1|2

Math
Sequences & SeriesFor the following geometric sequence find the recursive formula and the 5th term in the sequence. In
your final answer, include all of your work.
{-4, 12, -36,...}

Math
Sequences & SeriesFor the following geometric sequence find the explicit formula: (-1, 3, -9, ...).
an-3-an-1 where a=-1
an = (-3) -1
an-3 an-1 where a 1
an=-1-(-3) -1

Math
Sequences & SeriesFind the common ratio for the following sequence.
1/2, -1/4, 1/8, -1/16, ...
1/2
-2
-1/2
2


Math
Sequences & SeriesGiven the sequence 7, 14, 28, 56, which expression shown would give the tenth term?
7.29
7.210
710
....

Math
Sequences & SeriesWhich of the following is an arithmetic sequence?
-2, 4, -6, 8, ...
2, 4, 8, 16, ...
-8, -6, -4, -2, ...

Math
Sequences & SeriesA payday loan store charges $25 for a one-month loan of $240. What annual interest rate is this equivalent to?

Math
Sequences & SeriesFind the common difference for the sequence shown
1/4, 5/16, 3/8, ...
1/16
1/4
1/2

Math
Sequences & SeriesFind the common difference of the arithmetic sequence shown.
1/4 , 3/8, 1/2, ...

Math
Sequences & SeriesWhat is the common ratio of the following sequence?
-5, -20, -80, ...
04
04
-4

Math
Sequences & SeriesThe number of cars sold weekly by a new automobile dealership grows according to a linear growth
model. The first week the dealership sold six cars (Po= 6). The second week the dealership sold
cars (P₁ = 11).
Write the recursive formula for the number of cars sold, Pn, in the (n + 1)th week.
Pn=Pn-1 +
Write the explicit formula for the number of cars sold, Pn, in the (n + 1)th week.
Pn=
If this trend continues, how many cars will be sold in the sixth week?


Math
Sequences & SeriesFind the 30th term of the following sequence.
2, 8, 14, 20, ...
176
182
180
174
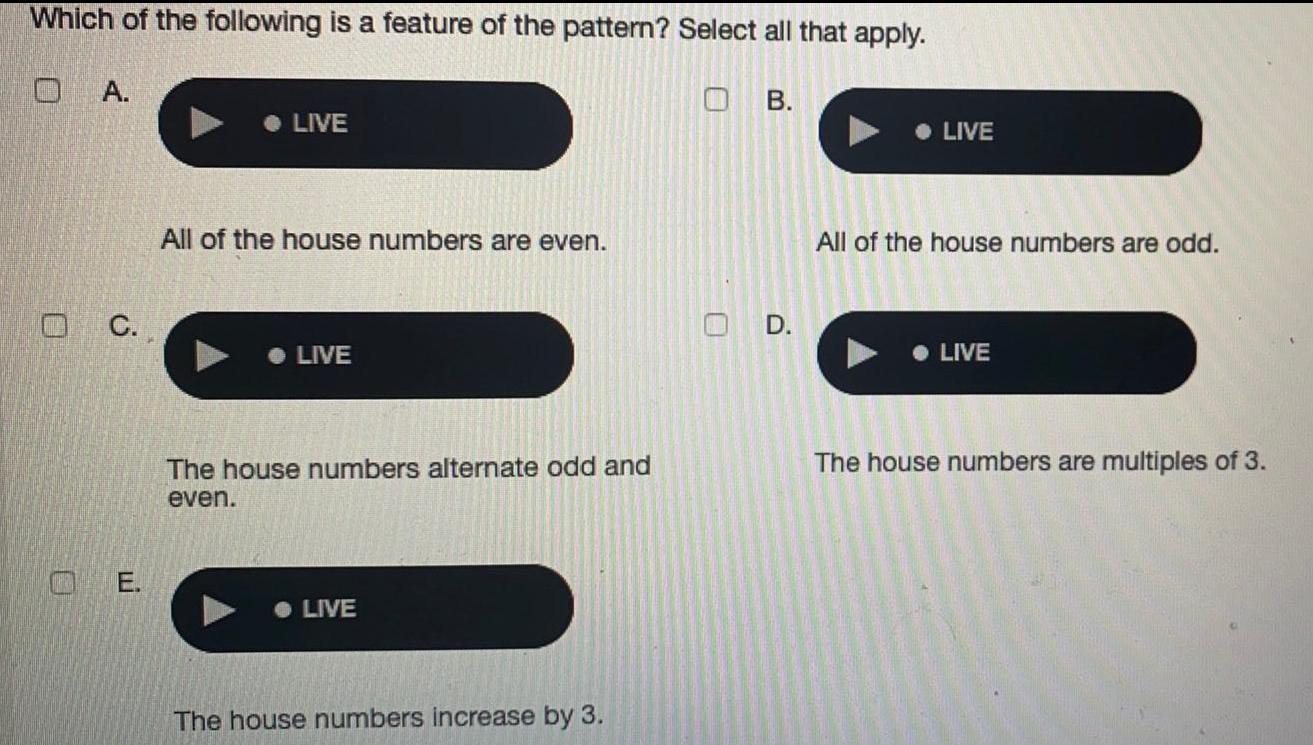
Math
Sequences & SeriesWhich of the following is a feature of the pattern? Select all that apply.
A. All of the house numbers are even.
B. All of the house numbers are odd.
C. The house numbers alternate odd and even.
D. The house numbers are multiples of 3.
E. The house numbers increase by 3.

Math
Sequences & SeriesAt the beginning of April, a colony of ants has a population of 5,000 ants.
a. The colony decreases by 1/5 during April. Write an expression for the ant population at the end of April.
b. The colony continues to decrease by % of its size each month. Write an expression for the ant population after 6 months.

Math
Sequences & SeriesA laptop computer is purchased for $4900. Each year, its value is 80% of its value the year before. After how many years will the laptop computer be worth
$1000 or less? (Use the calculator provided if necessary.)
Write the smallest possible whole number answer.

Math
Sequences & SeriesThe population of a certain bacteria can be modeled by the function P (t) = 2,000(1.034)t,
where t represents the number of hours after an experiment has started. What does 2,000
represent in the function?

Math
Sequences & SeriesState if the sequence is arithmetic, geometric, or neither. 1, 5, 35, 175, 875...
a. Arithmetic
b. Geometric
C. Neither
d. Doge to the moon
a
b
c
d

Math
Sequences & SeriesExplain how to find the domain of the geometric sequence where a₁ = 2 and the common ratio is 3.