Sequences & Series Questions and Answers

Math
Sequences & SeriesThe limit of the difference quotient, -21, from Part 1 above is (select all that apply).
A. ƒ(−2).
B. the slope of the tangent line to the graph of y = f(x) at x = -2.
C. the slope of the secant line to the graph of y = f(x) at x = -2.
D. the instantaneous rate of change of f at x = -2.
E. the average rate of change of fat x = -2.
F. f'(-2)
Math
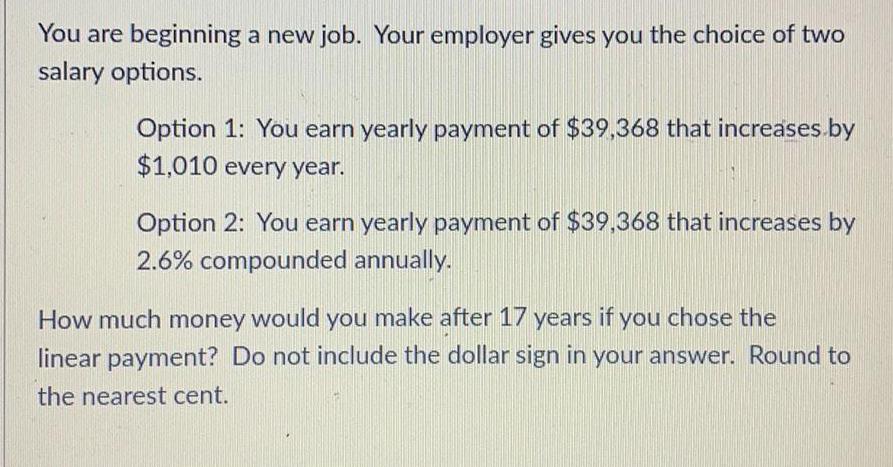
Sequences & SeriesYou are beginning a new job. Your employer gives you the choice of two
salary options.
Option 1: You earn yearly payment of $39,368 that increases by $1,010 every year.
Option 2: You earn yearly payment of $39,368 that increases by 2.6% compounded annually.
How much money would you make after 17 years if you chose the linear payment? Do not include the dollar sign in your answer. Round to the nearest cent.

Math
Sequences & SeriesA company currently sells 905 units per year of a particular product, and sales are growing at a rate of 8% each year. How many years will it be until they are selling 3,218 units per year? Give your answer to two decimal places.
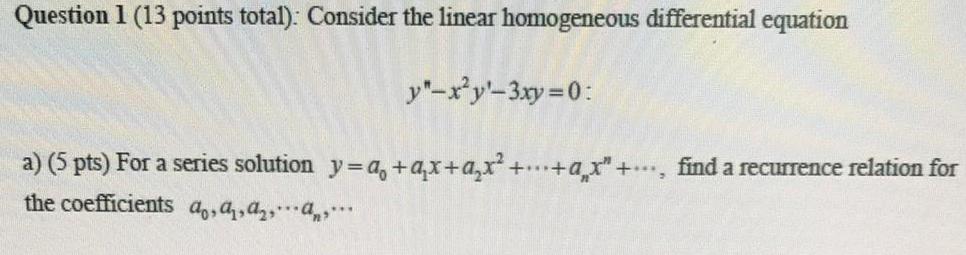
Math
Sequences & SeriesQuestion 1 (13 points total): Consider the linear homogeneous differential equation
y"-x²y'-3xy=0:
a) (5 pts) For a series solution y=a, +qx+a₂x²+...+₂x+, find a recurrence relation for
the coefficients a A₁, A₂, A

Math
Sequences & SeriesSelect the correct answer.
Bacteria begins to grow on the water's surface in a non-operational swimming pool on September 20. The bacteria grows and covers the water's surface in such a way that the area covered with bacteria doubles every day. If It continues to grow in this way, the water's surface will be entirely covered with bacteria on September 28.
When will a quarter of the water's surface be covered?
A The water's surface will be covered a quarter of the way on September 24.
B. The water's surface will be covered a quarter of the way on September 27.
C. The water's surface will be covered a quarter the way on September 26.
D. The water's surface will be covered a quarter of the way on September 25.

Math
Sequences & SeriesMia baked a very large apple pie that she cuts into slices to share with her friends. The
smallest slice is cut first. The volume of each successive slice of pie forms a geometric
sequence.
The second smallest slice has a volume of 30cm³. The fifth smallest slice has a volume of
240cm³.
Find the common ratio of the sequence.
Find the volume of the smallest slice of pie.
The apple pie has a volume of 61425cm³.
Find the total number of slices Mia can cut from this pie.

Math
Sequences & SeriesKendrick's hair was 10 centimeters long after his last haircut, and it grows 4 centimeters every year. Kendrick last got his hair cut 8 years ago. How long is it now?

Math
Sequences & SeriesA magazine had 4000 subscribers at the end of the year 2004. The number of subscribers increased by 10% each year as compared with the previous year. Which of the following is closest to the number of subscribers at the end of the year 2007?
4400
4330
5200
5320

Math
Sequences & SeriesIn 2016, 5,200 parking permits were issued in a city. The number of parking permits increases by 5% every year. Let y represent the number of parking permits issued xyears since 2016.
Which type of sequence does the situation represent?
A The situation represents an arithmetic sequence because the successive y-values have a common difference of 1.5.
B. The situation represents a geometric sequence because the successive y-values have a common ratio of 1.5.
C. The situation represents an arithmetic sequence because the successive y-values have a common difference of 1.05.
D. The situation represents a geometric sequence because the successive y-values have a common ratio of 1.05.

Math
Sequences & SeriesIf 26200 dollars is invested at an interest rate of 10 percent per year, find the value of the investment at the end of 5 years for the following compounding methods, to the nearest cent.
(a) Annual: $
(b) Semiannual: $
(c) Monthly: $
(d) Daily: $

Math
Sequences & SeriesImagine you are building a staircase with cubes. To build a staircase with one step, one cube is needed. To build a staircase with two steps, three cubes are needed. To build a staircase with three steps, six cubes are needed. Continue this pattern and determine how many cubes are needed to build a staircase with 50 steps, 250 steps, and x steps.
Math
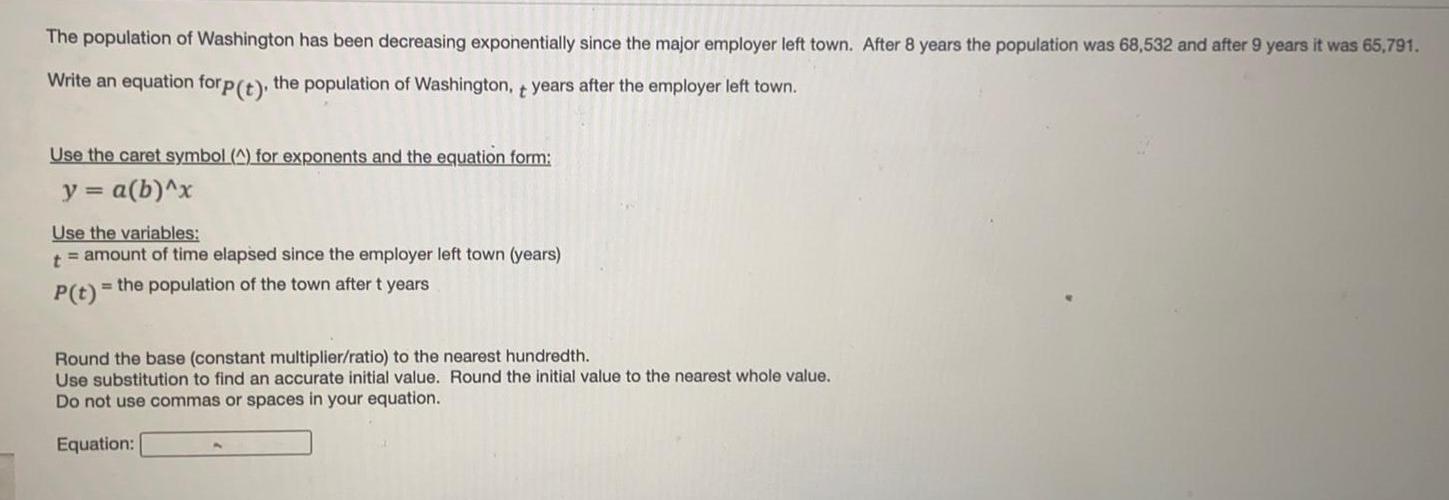
Sequences & SeriesThe population of Washington has been decreasing exponentially since the major employer left town. After 8 years the population was 68,532 and after 9 years it was 65,791.
Write an equation forp (t), the population of Washington, + years after the employer left town.
Use the caret symbol (^) for exponents and the equation form:
y = a(b)^x
Use the variables:
t = amount of time elapsed since the employer left town (years)
P(t) = the population of the town after t years
Round the base (constant multiplier/ratio) to the nearest hundredth.
Use substitution to find an accurate initial value. Round the initial value to the nearest whole value.
Do not use commas or spaces in your equation.
Equation:
![5. A sequence is defined by a₁ = 1, an+1 =1/2(an+3). Which of the following statements is
true?
(a) {an} is increasing and bounded above by.
(b) {an} is decreasing and bounded below by 1.
(c) {an] is decreasing and bounded below by 2.
(d) {an} is decreasing and bounded above by 2.
(e) {an} is increasing and bounded above by 3.](https://media.kunduz.com/media/sug-question/raw/43511503-1658251516.821821.jpeg?w=256)
Math
Sequences & Series5. A sequence is defined by a₁ = 1, an+1 =1/2(an+3). Which of the following statements is
true?
(a) {an} is increasing and bounded above by.
(b) {an} is decreasing and bounded below by 1.
(c) {an] is decreasing and bounded below by 2.
(d) {an} is decreasing and bounded above by 2.
(e) {an} is increasing and bounded above by 3.

Math
Sequences & SeriesThe bear population has a growth rate of 1.02. There are 1573 bears this year. Write a
function that models the bear population. How many bears will there be in 10 years?
a. Find the a and the b for this problem.
b. Write the equation that models this situation.
How many bears will there be in 10 years?

Math
Sequences & SeriesDetermine if the sequence below is arithmetic or geometric
and determine the common difference / ratio in simplest
form. This is common difference common ratio
20, 15, 10, ...

Math
Sequences & SeriesJack is a teacher and takes home 86 papers to grade over the weekend. He can grade at a rate of 11 papers per hour. Write a recursive sequence to represent how many papers Jack has remaining to grade after working for n hours.

Math
Sequences & SeriesThe first three terms of a sequence are given. Round to the nearest thousandth (if necessary).
312, 306, 300, ...
Find the 47th term.

Math
Sequences & SeriesWhich recursive sequence would produce the sequence
10, -25, 45, ...?
a₁ = 10 and an = -3an-1 + 5
a₁ = 10 and an =-5an-1-2
a₁ = 10 and an = -2an-1-5
a₁ = 10 and an = 5an-1-3
Math
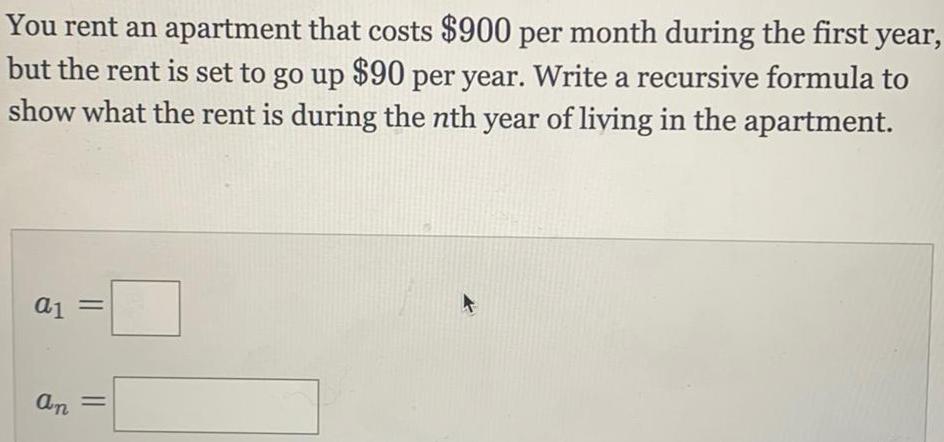
Sequences & SeriesYou rent an apartment that costs $900 per month during the first year, but the rent is set to go up $90 per year. Write a recursive formula to show what the rent is during the nth year of living in the apartment.

Math
Sequences & SeriesJacob is a teacher and takes home 58 papers to grade over the weekend. He can grade at a rate of 15 papers per hour. Write a recursive sequence to represent how many papers Jacob has remaining to grade after working for n hours.
ao
an

Math
Sequences & SeriesAn author published a book which was being sold online. The first month the author sold 3500 books, but the sales were declining steadily at 12% each month. If this trend continues, how many total books would the author have sold over the first 24 months, to the nearest whole number?

Math
Sequences & SeriesIn a lab experiment, the decay of a radioactive isotope is being observed. On the first day of the experiment the mass of the substance was 1200 grams and mass was decreasing by 11% per day. Write a recursive formula to represent the mass of the radioactive sample on the nth day of the experiment.

Math
Sequences & SeriesIan is a teacher and takes home 46 papers to grade over the weekend. He can grade at a rate of 11 papers per hour. Write a recursive sequence to represent how many papers Ian has remaining to grade after working for n hours.
ao =
an =

Math
Sequences & SeriesAubrey opened a savings account with $1400 that pays no interest. She deposits an additional $70 each week thereafter. Write a recursive formula to show how much money Aubrey has in the account n weeks after opening the account.
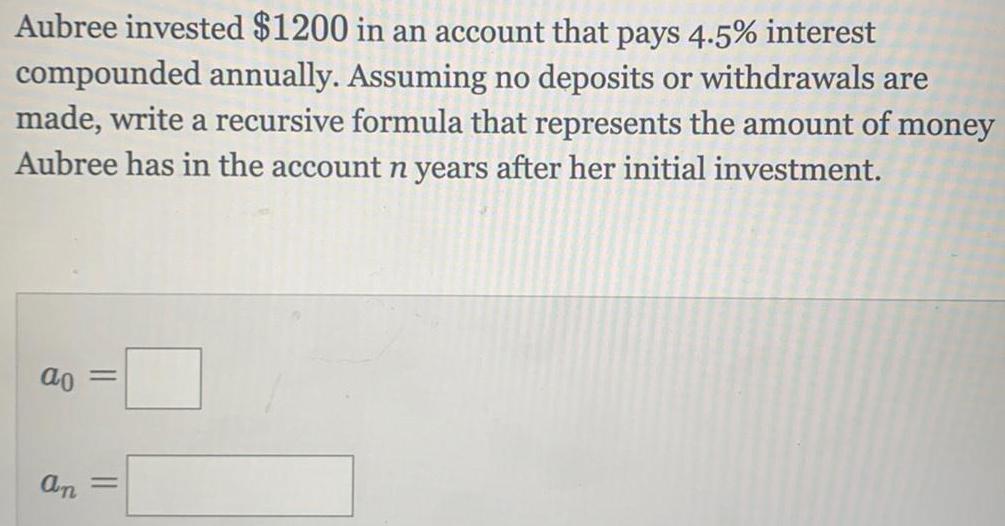
Math
Sequences & SeriesAubree invested $1200 in an account that pays 4.5% interest compounded annually. Assuming no deposits or withdrawals are made, write a recursive formula that represents the amount of money Aubree has in the account n years after her initial investment.
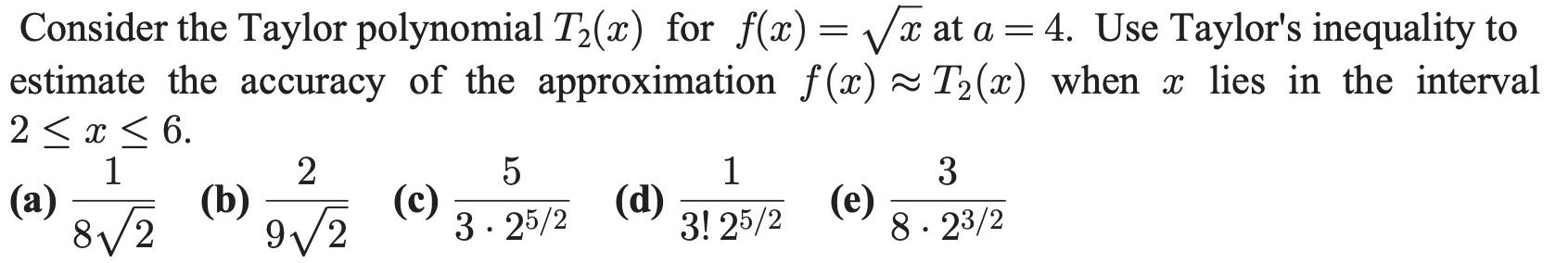
Math
Sequences & SeriesConsider the Taylor polynomial T₂(x) for f(x)=√x at a = 4. Use Taylor's inequality to estimate the accuracy of the approximation f(x)≈ T₂(x) when x lies in the interval 2 ≤ x ≤ 6.
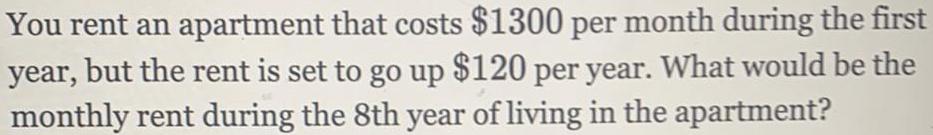
Math
Sequences & SeriesYou rent an apartment that costs $1300 per month during the first year, but the rent is set to go up $120 per year. What would be the monthly rent during the 8th year of living in the apartment?
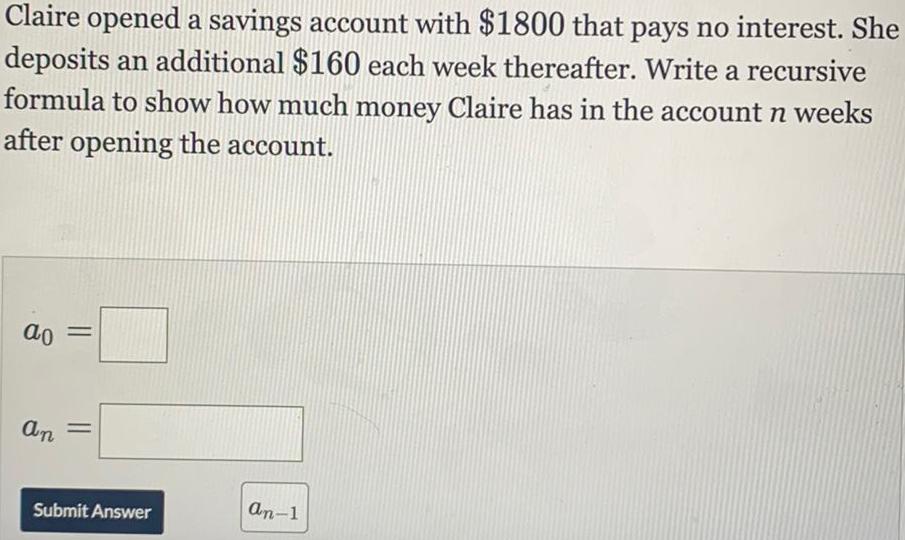
Math
Sequences & SeriesClaire opened a savings account with $1800 that pays no interest. She
deposits an additional $160 each week thereafter. Write a recursive
formula to show how much money Claire has in the account n weeks
after opening the account.
ao =
an


Math
Sequences & SeriesThe numbers of seats in the first 12 rows of a high-school auditorium form an arithmetic sequence. The first row has 9 seats. The second row has 11 seats.
a. Write a recursive formula to represent the sequence.
b. Write an explicit formula to represent the sequence.
c. How many seats are in the 12th row?
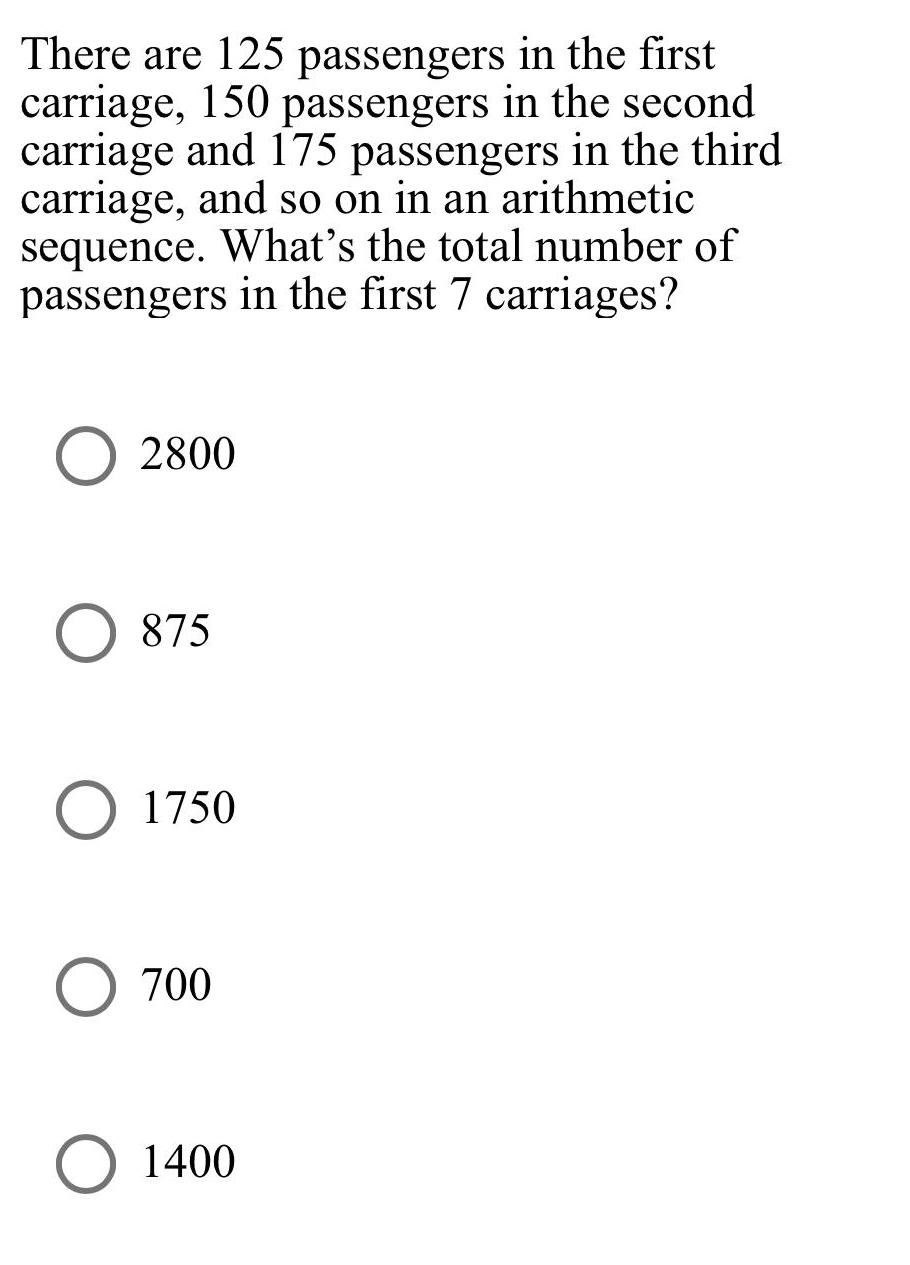
Math
Sequences & SeriesThere are 125 passengers in the first
carriage, 150 passengers in the second
carriage and 175 passengers in the third
carriage, and so on in an arithmetic
sequence. What's the total number of
passengers in the first 7 carriages?
2800
875
1750
700
1400
![Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that R(x) → 0.]
f(x) = In(x),
a = 6
f(x) = In(6) +
Ž
n = 1
Find the associated radius of convergence R.
R =](https://media.kunduz.com/media/sug-question/raw/59971577-1658211878.4756584.jpeg?w=256)
Math
Sequences & SeriesFind the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that R(x) → 0.]
f(x) = In(x),
a = 6
f(x) = In(6) +
Ž
n = 1
Find the associated radius of convergence R.
R =
![Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that R(x) → 0.]
f(x) = e-4x](https://media.kunduz.com/media/sug-question/raw/59971639-1658211054.327143.jpeg?w=256)
Math
Sequences & SeriesFind the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that R(x) → 0.]
f(x) = e-4x

Math
Sequences & SeriesWhat is the next fraction in this sequence? Simplify your answer.
4/9, 7/18, 1/3, 5/18, ...

Math
Sequences & SeriesTara owns a pizza shop. The item purchased most frequently from her shop is a large pizza. For any order, Tara charges $7.00 for each pizza plus $3.00 for delivery services. Tara made a delivery of pizzas to a party for which she charged $45.00. How many pizzas did she deliver?
Only an algebraic solution will be accepted.

Math
Sequences & SeriesGiven nt+1= = nt + 3.6 and n4 = 12.6:
a) Make a table for the first five terms.
b) Find n20 and n_22.
c) Find the t for which n 102.6 and nt = -70.2.
d) Write an algebraic representation for this sequence.

Math
Sequences & SeriesSuppose the newest version of your favorite Smartphone comes out today. Assume that a total of 20 people goes to your local cell phone dealer to purchase this phone today and that each day the total number of people who purchase the Smartphone doubles. How many people have purchased the Smartphone 5 days from today? {your answer just a number}
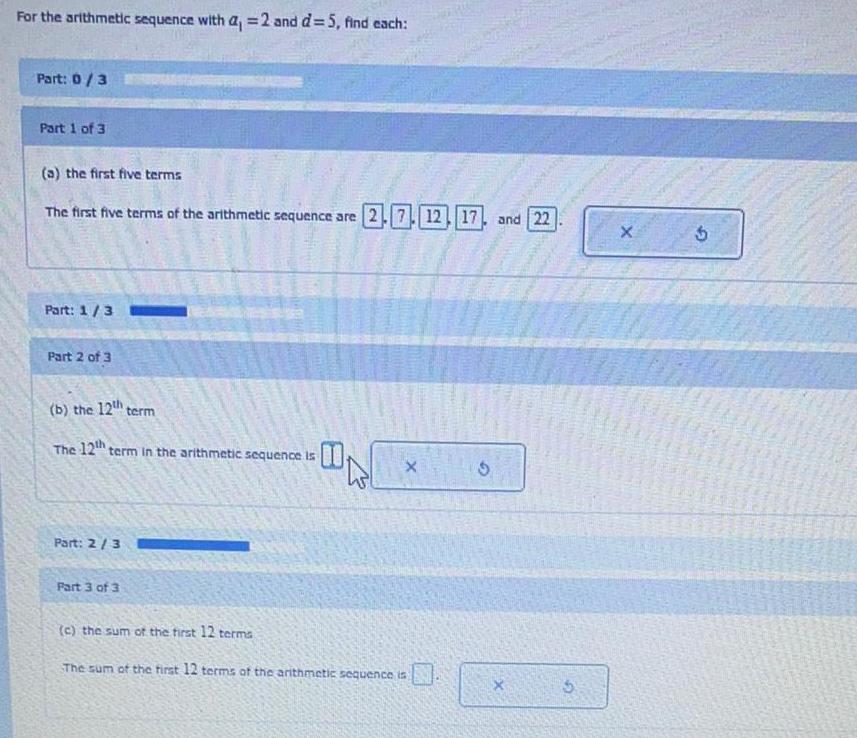
Math
Sequences & SeriesFor the arithmetic sequence with a, = 2 and d=5, find each:
(a) the first five terms
The first five terms of the arithmetic sequence are
(b) the 12th term
The 12th term in the arithmetic sequence is
(c) the sum of the first 12 terms
The sum of the first 12 terms of the arithmetic sequence is
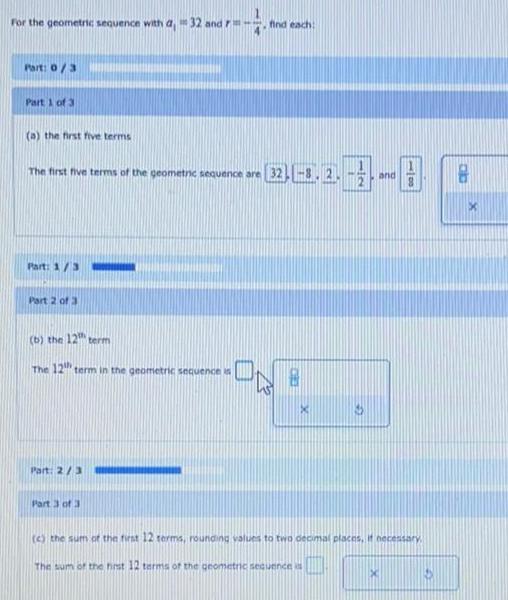
Math
Sequences & SeriesFor the geometric sequence with a 32 and r= -1/4, find each
(a) the first five terms
(b) the 12 term
(c) the sum of the first 12 terms, rounding values to two decimal places, if necessary
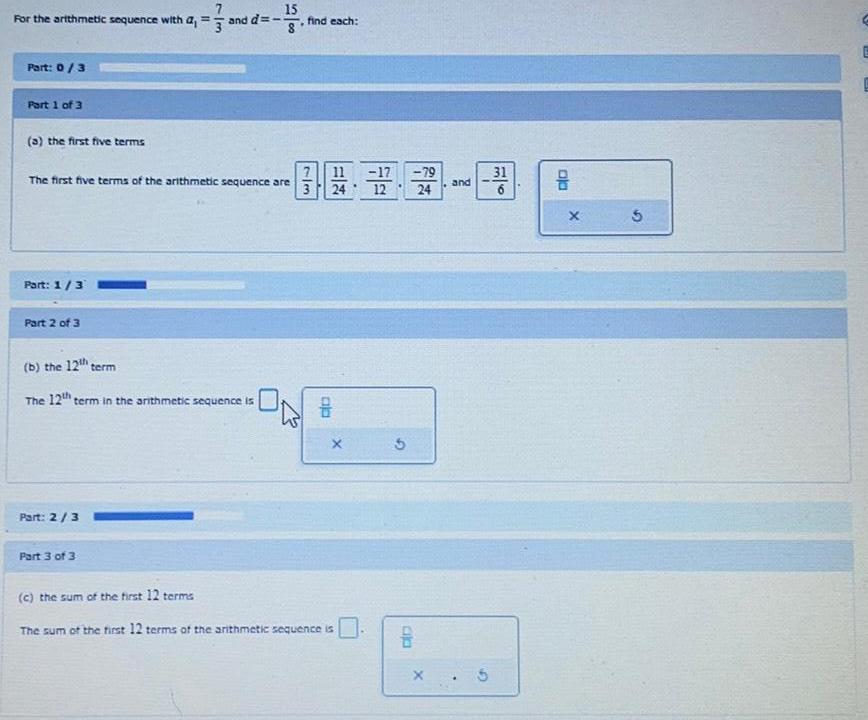
Math
Sequences & SeriesFor the arithmetic sequence with a₁ =7/3 and d=-15/8
Part 1 of 3
(a) the first five terms
The first five terms of the arithmetic sequence are
(b) the 12th term
(c) the sum of the first 12 terms

Math
Sequences & SeriesElement X decays radioactively with a half life of 14 minutes. If there are 230 grams
of Element X, how long, to the nearest tenth of a minute, would it take the element to
decay to 3 grams?
y = a(.5)

Math
Sequences & SeriesDetermine if the sequence is arithmetic. If it is, find the common difference and the explicit formula.
-22, 122, -222, -322, ..
Math
Sequences & SeriesMrs Brown has $1000 to invest into an account that earns 7% interest each year. Would this be arithmetic or geometric?
geometric
arithmetic
No answer text provided.
No answer text provided.

Math
Sequences & SeriesFind the common difference and the explicit formula.
21, 179, -379, -579, ...
Common Difference: d = - 200
Explicit: an = 221 - 200n
Common Difference: d = - 202
Explicit: an = 20 - 202n
Common Difference: d = - 200
Explicit: an = = 21 - 200n
Common Difference: d = -200
Explicit: an = 18 - 200n
Common Difference: d= -200
Explicit: an = 20 - 200n

Math
Sequences & Series6, 7, 13, 20, 33, 53,
Select the correct choice below and, if necessary, fill in the answer box to complete your ch
A. The sequence is geometric. The next term is 6, 7, 13, 20, 33, 53,
B. The sequence is arithmetic. The next term is 6, 7, 13, 20, 33, 53, 86
C. The sequence is neither arithmetic nor geometric.
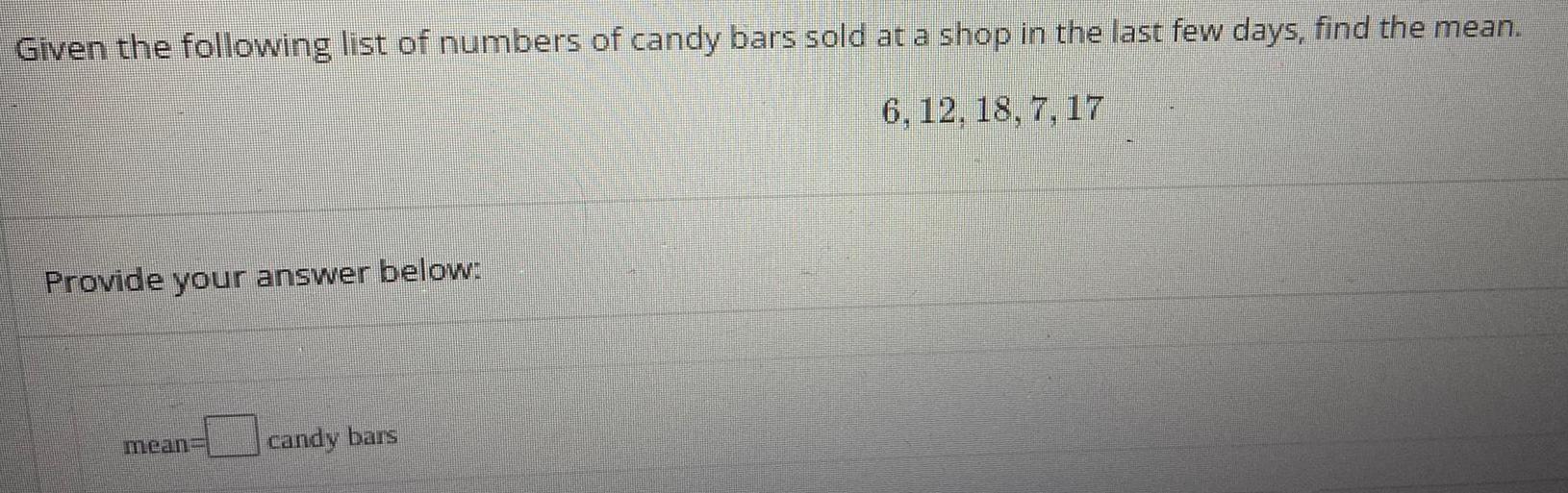
Math
Sequences & SeriesGiven the following list of numbers of candy bars sold at a shop in the last few days, find the mean.
![Determine how many primes there are in the ranges: 1-1000, 1001-2000, and so on up to 9001-10000. Can you see why the Greeks might have wondered if they would run out? (Hint: there are a number of websites that have lists of prime numbers. Even easier: use the Mathematica command Prime Pi[k] which gives the number of primes less than or equal to k.)](https://media.kunduz.com/media/sug-question/raw/55436947-1658081847.9169495.jpeg?w=256)
Math
Sequences & SeriesDetermine how many primes there are in the ranges: 1-1000, 1001-2000, and so on up to 9001-10000. Can you see why the Greeks might have wondered if they would run out? (Hint: there are a number of websites that have lists of prime numbers. Even easier: use the Mathematica command Prime Pi[k] which gives the number of primes less than or equal to k.)

Math
Sequences & Series8. Sally, Mariah, and Devin visit a bakery. Sally buys 3 biscuits and 2 muffins for $10.50. Mariah buys 2 muffins and 2 cupcakes for $14.00. Devin purchases 2 biscuits and 1 cupcake for $7.00. (4 points)
a. Set up a matrix equation that can be used to find the prices of biscuits, muffins, and cupcakes at the bakery using the information given. (3 points)
b. Find the price of a biscuit, the price of a muffin, and the price of a cupcake at the coffee shop. (1 point)

Math
Sequences & SeriesMr. Murphy's company used a total of 5000 gallons of gasoline in the year 2007. Mr. Murphy planned to reduce the amount of gasoline used by his company each year by 10% from the previous year. Based on Mr. Murphy's plan, what is the total amount of gasoline that his company will use in the year 2010?

Math
Sequences & SeriesA pair of women's running shoes cost $110 in 2004 and the same shoes cost $135 in 2008 due to inflation.
a. Develop an exponential model to describe the rate of inflation over this time period.
b. If inflation continues at the same rate, use your model in part (a) to estimate the price of the shoes in 2013.
a. The rate of inflation can be modeled by the following exponential equation, where the model solves for the inflated price y after time x.