Trigonometry Questions and Answers
Math
TrigonometryA person who is 1.65m high, stands 25.7m from the base of a building. She looks up atthe top of a near building at an angle of elevation of 35.4°.
a) Draw a diagram labelling all important information.
b) Calculate the height of the building (in meters to the nearest tenth).
Math
TrigonometryGiven that sec(θ)=√10 and θ is in Quadrant IV, what is tan(θ)?
Select the correct answer below:
√10/3
-√10/3
1/3
3
-3
-1/3

Math
TrigonometryA camper wants to protect her bag of food from bears. She decides to tightly stretch a rope
between two trees and hang her bag from a point exactly halfway along the length of the rope.
The first tree is 10 feet east and 6 feet north of her firepit. The second tree is 5 feet west and 8
feet north of her firepit. The rope is attached at a height of 8 feet to the first tree and a height of
9 feet to the second tree.
Let the firepit represent the origin, movement east of the firepit represent movement in the
direction of positive x, movement west of the firepit represent movement in the direction of
negative x, movement north of the firepit represent movement in the direction of positive y,
and movement above the firepit represent movement in the direction of positive z.
1. Write the coordinates of the points on the trees where the rope is attached.
2. Find the distance between the points in part a. Use "sqrt ()" to indicate a square root.
For example, √√3 would be written sqrt (3).
3. Find the coordinates of the point where the food bag is hung.
4. If the food bag is 1.2 feet long when hung and bears can reach a height of 7.5 feet when
standing, is the camper's food safe from bears? Explain why or why not.

Math
TrigonometryA 24-foot ladder rests against a house near a second story window 20 feet from the ground. Assume that the ladder and the house both sit on level ground.
To the nearest whole number, find the following values:
A. The measure of the angle formed by the base of the ladder and level ground is
B. The measure of the angle formed by the top of the ladder and the second story window is
C. The distance, on level ground, between the base of the ladder and the house is feet.

Math
TrigonometryThe top of a 22-foot ladder rests against the top of an 18-foot wall. If the base of the ladder is on the same ground level as that of wall, what angle does the ladder form with the ground? Express your solution to the nearest degree.

Math
TrigonometryAs shown in the diagram, a ship sails 16 nautical miles east from a harbor. It then sails 18 nautical miles in the direction of
N 55° E. How far is it from the harbor to the nearest nautical mile?
16
O 11 nautical miles
O 24 nautical miles
O 32 nautical miles
O 36 nautical miles
155° 18
Math
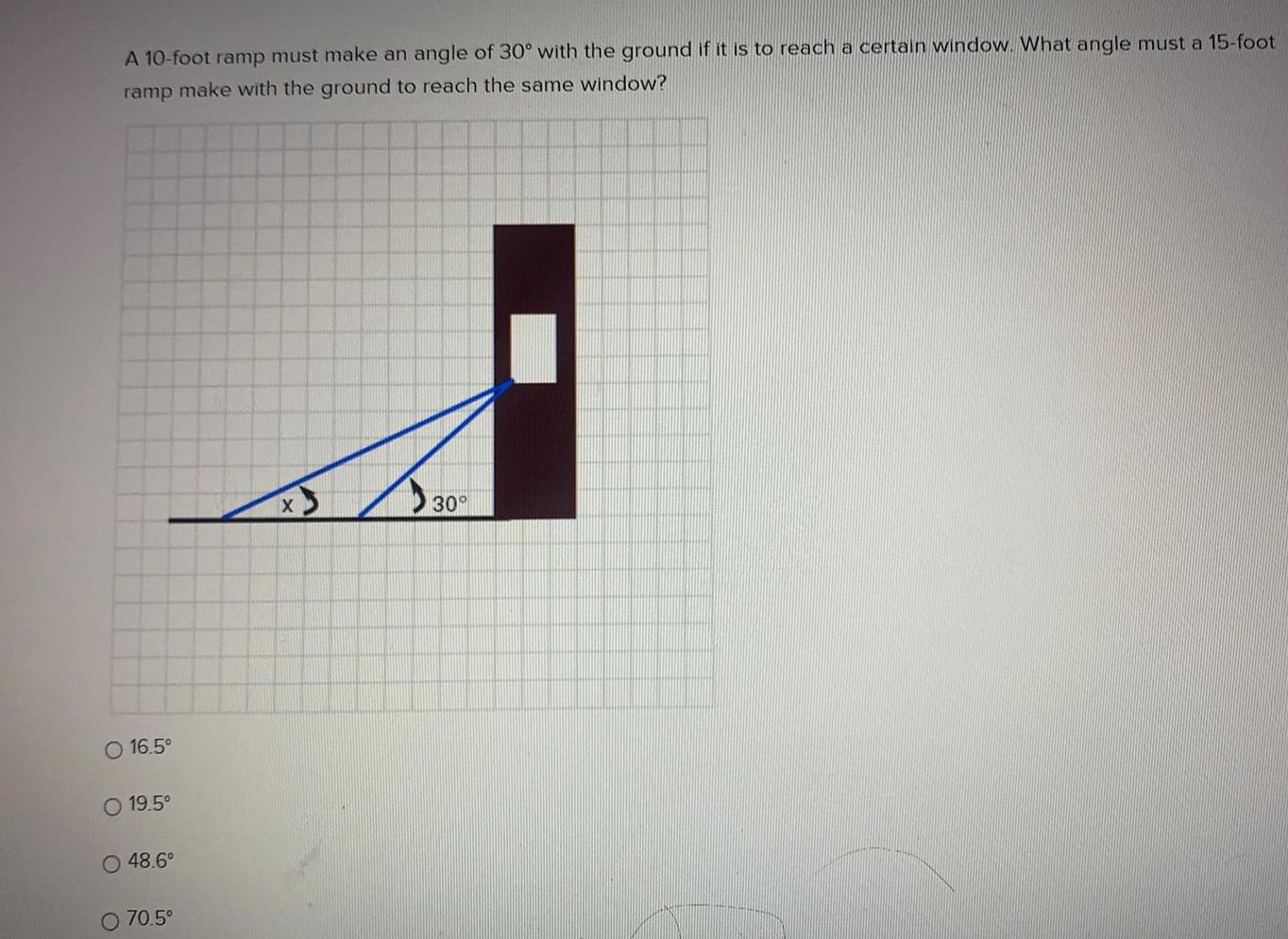
TrigonometryA 10-foot ramp must make an angle of 30° with the ground if it is to reach a certain window. What angle must a 15-foot
ramp make with the ground to reach the same window?
O 16.5°
O 19.5°
O48.6°
O 70.5°
X
30°
Math
TrigonometrySolve the equation on the interval 0 ≤θ<2π.
sin(2θ) =
What are the solutions to sin (2) =

Math
TrigonometrySolve the equation. Give a general formula for all the solutions. List six solutions.
cosθ= 0
Write the general form for all the solutions to cos 0 = 0 based on the smaller angle.

Math
TrigonometrySuppose that the point (-1,- 6) lies on the terminal side of an angle 0. Enter the exact values of the
trig functions below:
cos(0) =
cot (0) =
tan(0) =
csc (0)
sec (0) =
sin(0) =
=

Math
TrigonometryPart A: Given sinθ=√3/2 , determine three possible angles θ on the domain [0,∞).
Part B: Given θ = 675°, convert the value of θ to radians and find sec θ.
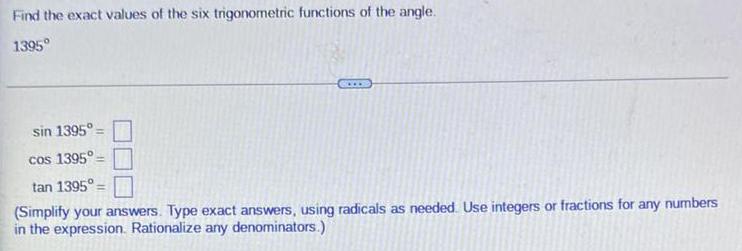
Math
TrigonometryFind the exact values of the six trigonometric functions of the angle.
1395⁰
sin 1395°
cos 1395°
tan 1395°

Math
TrigonometryWhen tuning a piano, a technician strikes a tuning fork for the A above middle C and sets up a wave motion that can be approximated by y = 0.001 sin(880πt), where t is the time (in seconds
(a) What is the period p of the function?
sec
(b) The frequency f is given by f =1/p
cycles per second
What is the frequency of the note?

Math
TrigonometryA power failure on the bridge of a Great Lakes freighter has resulted in the ship's
navigator having to do her own calculations. She measures the angle between the
ship's course and a lighthouse on shore as 32°. After the ship has travelled 1500 m,
she measures the angle to be 72°. Determine if the ship was closer to or farther from
the lighthouse at the second sighting, and by what distance. (4 marks)

Math
TrigonometryAlthough 240° is a special angle on the unit circle, Aiden wanted to determine its coordinates using the sum and difference formulas.
Part A: Determine cos 240° using the cosine sum identity. Be sure to include all necessary work. (5 points)
Part B: Determine sin 240° using the sine difference identity. Be sure to include all necessary work. (5 points)

Math
TrigonometryA triangular lot bounded by 3 streets has a frontage of 300 feet on one street, 250 feet on the second, and 420 feet on the third. Find the measure of the largest angle between the two streets bounding the lot.
81°
99°
135°

Math
TrigonometryThe terminal side of angle B in standard position goes through the point (11,-11). Find the values of the six trigonometric functions of B. Please round your answers to 1 decimal place.

Math
TrigonometryIn triangle ABC, angle C is a right angle. Find the value of the trig function.
Find the sec(A) if c = 25, b=20, a=15
5/3
4/5
5/4
1
None of the other answers are correct

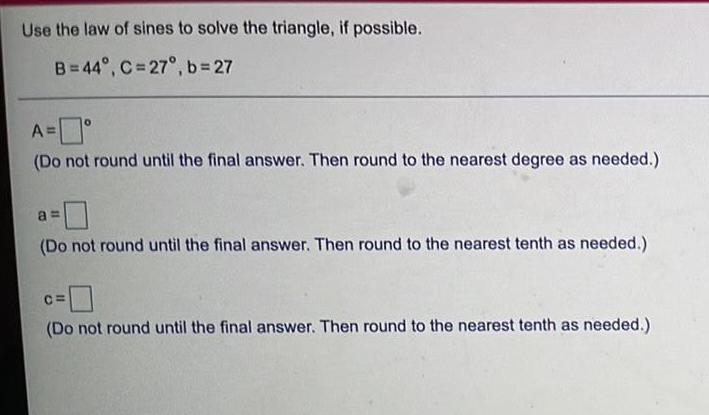
Math
TrigonometryUse the law of sines to solve the triangle, if possible.
B=44°, C=27°, b=27
A=0°
(Do not round until the final answer. Then round to the nearest degree as needed.)
a=
(Do not round until the final answer. Then round to the nearest tenth as needed.)
C=
(Do not round until the final answer. Then round to the nearest tenth as needed.)

Math
TrigonometryFirst, determine the quadrant for 0; then find z, y, and r; and finally, give all six trigonometric ratios for given the following information:
cos(θ) = -8/13 and tan (θ) <0
θ lives in quadrant
Note: You can earn partial credit on this problem.
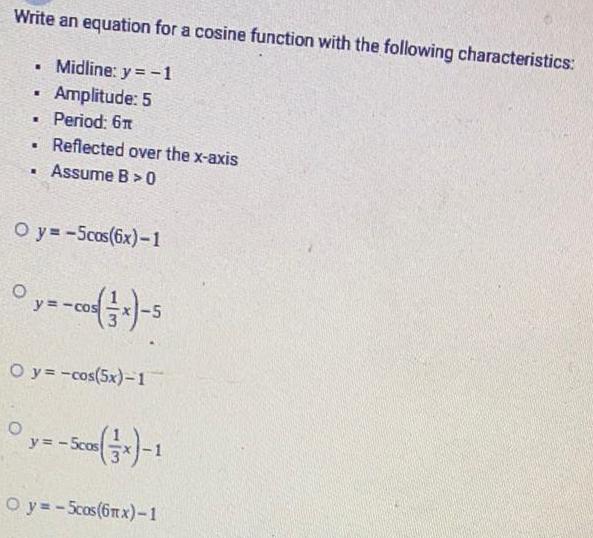
Math
TrigonometryWrite an equation for a cosine function with the following characteristics:
Midline: y = -1
Amplitude: 5
.
▪
▪ Period: 6m
.
Reflected over the x-axis
. Assume B>0
Oy=-5cos(6x)-1
0y=-cos(x)-5
O y=-cos(5x)-1
y=-Scon(x)-1
Oy=-5cos(6mx)-1
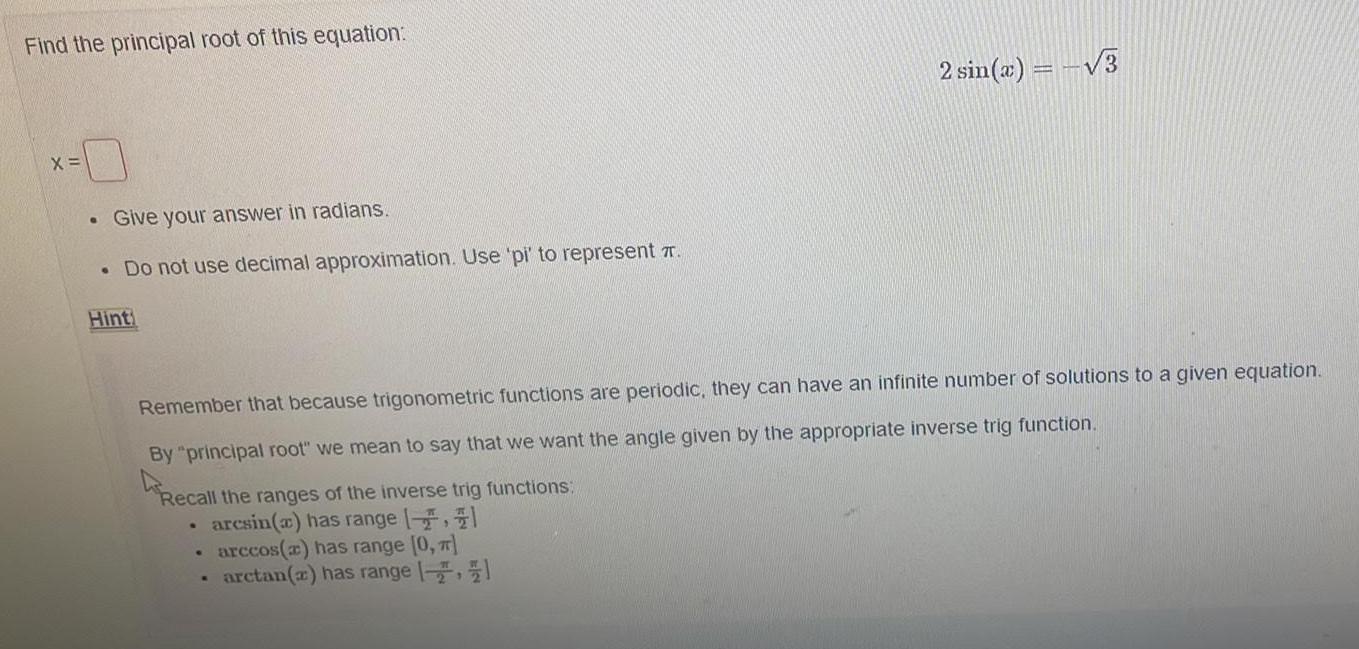
Math
TrigonometryFind the principal root of this equation:
2sin(x)= -√3
X =
Give your answer in radians.
Do not use decimal approximation. Use 'pi' to represent π.
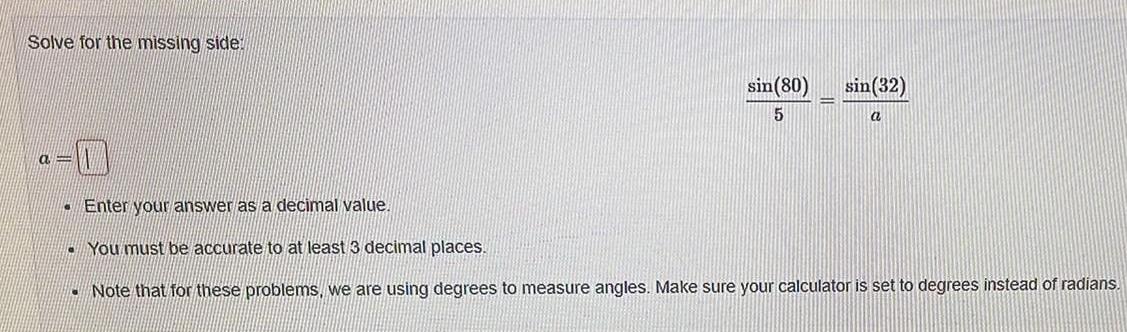
Math
TrigonometrySolve for the missing side: sin(80)/5 = sin(32)/a
Enter your answer as a decimal value.
You must be accurate to at least 3 decimal places.
Note that for these problems, we are using degrees to measure angles. Make sure your calculator is set to degrees instead of radians.
Math
Trigonometryt
612
Draw and label the sides and angles of a triangle for which the tangents of the
acute angles are equal to 1.
2

Math
TrigonometryThe angle of elevation of the sun is 35° from the ground. A business building downtown is 50 m tall. How long is the shadow cast by the building?

Math
TrigonometryA flagpole 94.8 ft tall is on the top of a building. From a point on level ground, the angle of elevation of the top of the flagpole is 34.8°, while the angle of elevation of the bottom of the flagpole is 25.8°. Find the height of the building.
The building is about ft tall.
(Round to the nearest foot as needed.)
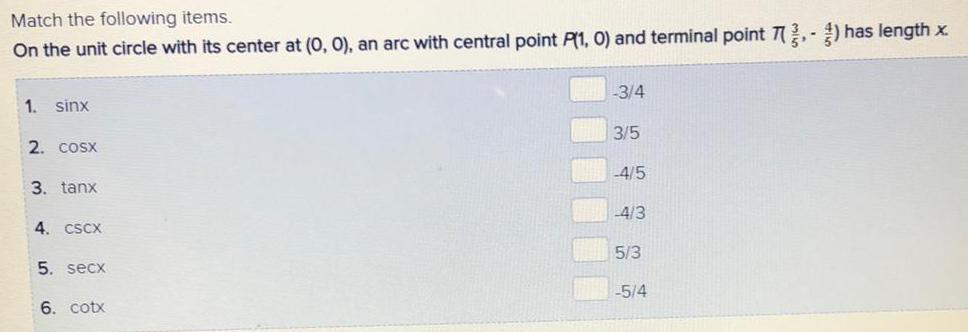
Math
TrigonometryMatch the following items.
On the unit circle with its center at (0, 0), an arc with central point P(1, 0) and terminal point T(3/5, -4/5) has length x.
1 sinx
2. cosx
3. tanx
4. CSCX
5. secx
6. cotx
-3/4
3/5
-4/5
-4/3
5/3
-5/4

Math
TrigonometryA ladder leaning against the side of a building makes a 70° angle with the ground. If the base of the ladder is 4 feet away from the bottom of the building, approximately how long is the ladder?
sin 70°= 0.9
cos 70°=0.3
tan 70° = 2.7
A 4.4 ft
B 10.8 ft
C 13.3 ft
D 21.0 ft

Math
TrigonometryA flagpole casts a 13-foot shadow on the ground when the sun is at a 68° angle of elevation. Which of the following expressions can be used to determine the height (h), in feet, of the flagpole? (Assume the flagpole is perpendicular to the ground.)
cos68=
cot68=
sin68=
tan68=

Math
TrigonometryVerify that the equation is an identity.
sec x - cos x = sin x tan x
To verify the identity, start with the more complicated side and transform it to look like the other side. Choose the correct transformations and transform the expression at each step.
sec x - cos x = - cos x
![Let f be the function defined by f(x) = sin(x). What is the average
value of f on the interval [4/3,8/3] written in simplest form?](https://media.kunduz.com/media/sug-question/raw/61083909-1657297387.1702414.jpeg?w=256)
Math
TrigonometryLet f be the function defined by f(x) = sin(x). What is the average
value of f on the interval [4/3,8/3] written in simplest form?

Math
TrigonometryGiven the following information, use the Pythagorean Identity or the alternate forms
of the Pythagorean Identity to find the values of the other five trigonometric
functions.
cos(t) = 2/3 and t is in the 4ᵗʰ quadrant.
tan(t) = 12/5 and 0 ≤ t < π/2
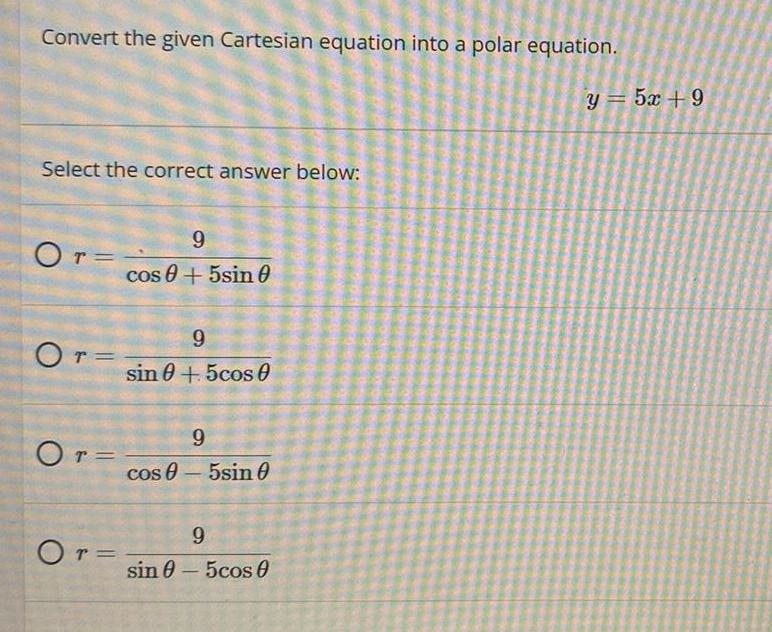
Math
TrigonometryConvert the given Cartesian equation into a polar equation.
Select the correct answer below:
r=9/(cosθ+5sinθ)
r=9/(sinθ+5cosθ)
r=9/(cosθ-5sinθ)
r=9/(sinθ-5cosθ)

Math
TrigonometryConsidering expression only the values of a for which the is defined, which of the following is equivalent to the expression below?
cos(-a).tana.csc(-a).cot(-a)
Select the correct answer below:
-cot a
csc a sec a cos a
-csc a sec a cos a
cot a

Math
TrigonometryWhen a wave hits an ocean buoy, it bobs up and down
so that the movement over time can be described by a
sine function.
Suppose the buoy travels 1 meter from its high point to
its low point and completes 20 cycles per second.
Which equation BEST represents h, the height of the
buoy in meters relative to its position on a calm ocean,
as a function of t, the time in seconds?
h = sin(20nt)
h = sin(40nt)
h= 20 sin(2nt)
h=0.5 sin (40nt)

Math
TrigonometrySimplify the following trigonometric expression,
considering only the values of a for which the
expression is defined
cos(a) tan(a) sec(a) cot(a)
Remember to put the arguments of any
trigonometric functions in parentheses.
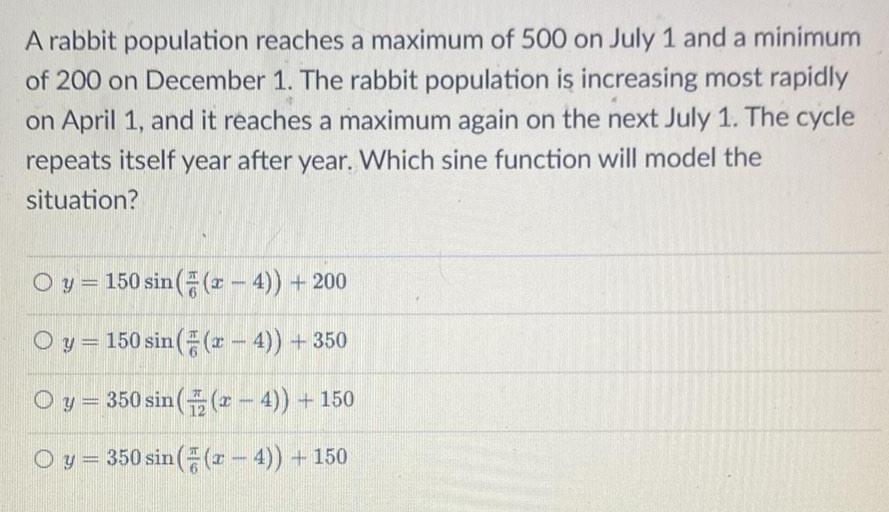
Math
TrigonometryA rabbit population reaches a maximum of 500 on July 1 and a minimum
of 200 on December 1. The rabbit population is increasing most rapidly
on April 1, and it reaches a maximum again on the next July 1. The cycle
repeats itself year after year. Which sine function will model the
situation?
y = 150 sin(π/6(x-4)) + 200
y = 150 sin(π/6((x-4)) +350
y = 350 sin(π/12((x-4)) + 150
y = 350 sin(π/6((x - 4)) + 150

Math
TrigonometryWhich statement is correct about the parent sine function?
The amplitude is 0 and the maximum value is y=1.
The midline is y=0, the amplitude is 1, and the minimum value is y = -1.
The period is 27 and the phase shift is .
The phase shift is, the midline is x=0, the amplitude is 1, and the minimum value is y = -1.

Math
TrigonometryThe angle of depression of an object refers to the angle whose initial side is a horizonal line above the object
and whose terminal side is the line-of-sight to the object below the horizontal.
From a fire tower 200 feet above level ground in the Sasquatch National Forest, a ranger spots a fire off in the
distance. The angle of depression to the fire is 2.2°. How far away from the base of the tower is the fire?
ft
Give the exact answer. You'll need to convert your angle into radians.
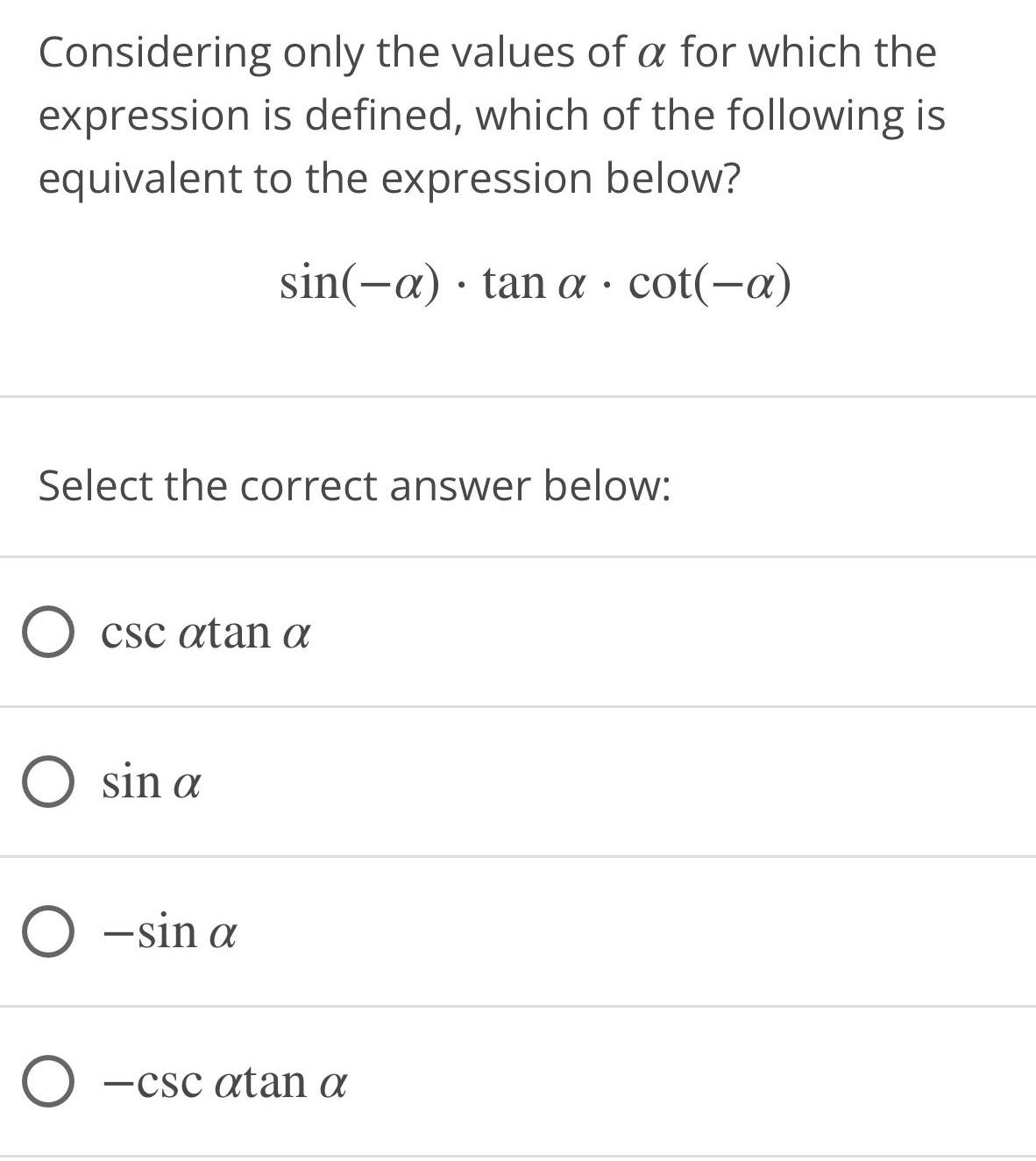
Math
TrigonometryConsidering only the values of α for which the expression is defined, which of the following is
equivalent to the expression below?
sin(-a) tan a cot(-a)
Select the correct answer below:
csc αtan α
sin α
-sin α
−csc αtan α

Math
TrigonometryNora is certain that cos(x + 2) = sinx. She is mistaken.
Note: The unit circle could be very helpful in thinking about why Nora is mistaken and about the next questions. The graphs could also be very helpful.
a. Show clearly that she is mistaken.
b. Now use another method to show her why she is mistaken.
c. Write an equation that relates the sin and cosine functions that is correct.
d. Explain how you can check that your equation is correct.

Math
TrigonometryChoose your own numbers (other than 1 or 0) for the parameters: a, b, c, and d in
y = asin(bx + c) + d.
a. Use Desmos to draw your graph and show a carefully drawn and scaled part of the graph for at least one full period. Explain its relation to the graph of y = sinx
Note: Once you put your graph is Desmos you might find out that you don't like the numbers you chose. Remember you can change them and make adjustments so you can work with numbers and a graph you like better. Each person should have a different solution!
b. For each parameter, give a new possible value to get your graph to:
Shift up
Shift to the left
Stretch vertically
Stretch out horizontally
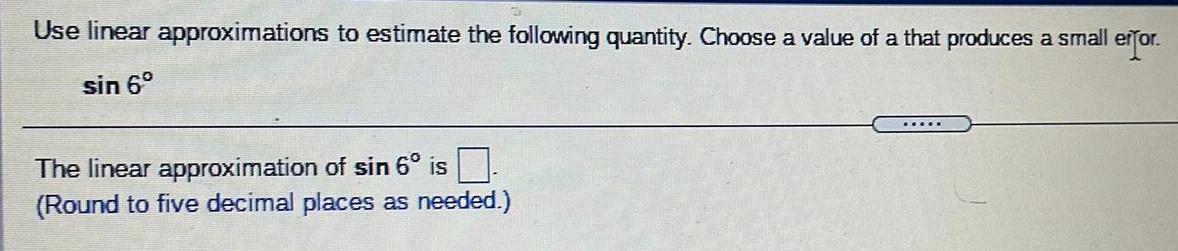
Math
TrigonometryUse linear approximations to estimate the following quantity. Choose a value of a that produces a small error.
sin 6°
The linear approximation of sin 6° is
(Round to five decimal places as needed.)

Math
Trigonometry5. An airplane is travelling at a speed of 400 miles per hour with a bearing of 200 degrees. The plane
encounters a wine blowing with a velocity of 60 miles per hour 40 degrees South of west. What are the
resultant speed and bearing of the airplane?

Math
TrigonometryTwo soccer players are warming up by kicking soccer balls at a goalie. The two players are located 10 yards apart, and the angle from each player to the goalie is 63° and 75°, respectively.
What is the distance from the farthest soccer player to the goalie?
14.436 yards
13.316 yards
10.841 yards
4.23 yards

Math
TrigonometryWhen shelled corn is stored in a cone-shaped pile 20 feet high, the diameter of the pile's
base is about 94 feet.
(b) Find the angle of repose for shelled corn. (Round your answer to one decimal place.)
(c) How tall is a pile of shelled corn that has a base diameter of 80 feet? (Round your answer to one decimal place.)
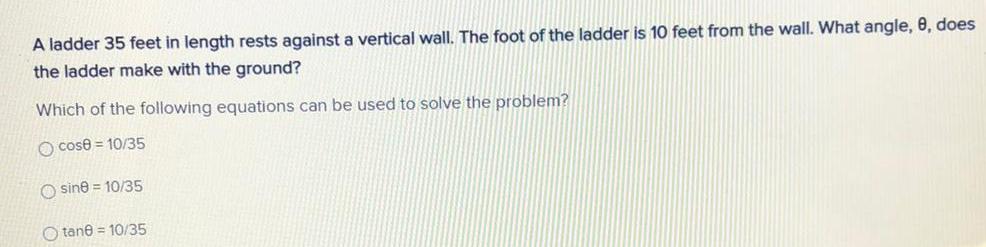
Math
TrigonometryA ladder 35 feet in length rests against a vertical wall. The foot of the ladder is 10 feet from the wall. What angle, 8, does the ladder make with the ground? Which of the following equations can be used to solve the problem?
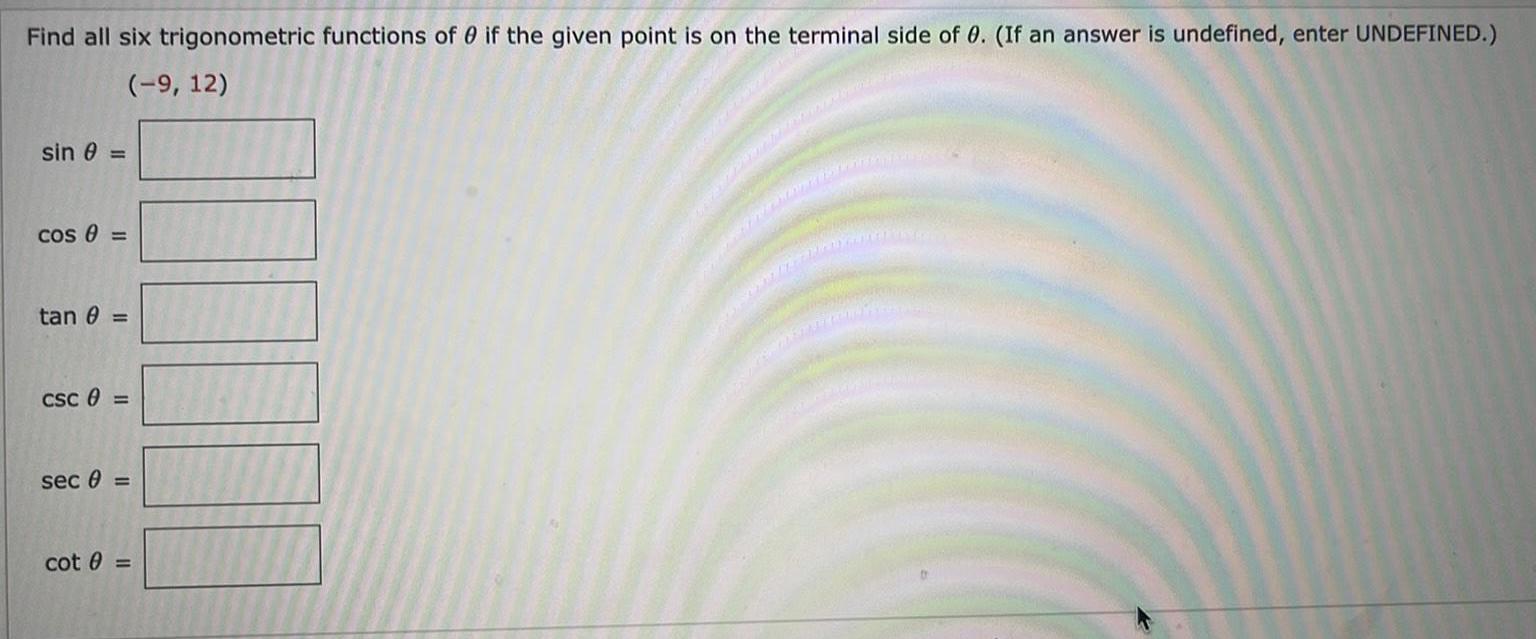
Math
TrigonometryFind all six trigonometric functions of 0 if the given point is on the terminal side of 0. (If an answer is undefined, enter UNDEFINED.)
(-9, 12)

Math
TrigonometryJuliet stands at the window of her apartment so that her eyes are 38.4 feet above the
ground. Juliet spots her boyfriend down the street a few blocks away. She knows, based
off the number of city blocks, that her boyfriend is at a distance of 156.45 feet away from
the building. Determine the angle of depression of Juliet's site to her boyfriend on the
ground.