Trigonometry Questions and Answers

Math
TrigonometryWithout using a calculator, compute the sine and cosine 5π/3 of by using the reference angle.
What is the reference angle?
In what quadrant is the original angle?

Math
TrigonometryUse the unit circle, along with the definitions of the circular functions, to find the
exact values for the given functions when s= -2π.
sin (-2π), cos (-2π), tan (-2π)
Math
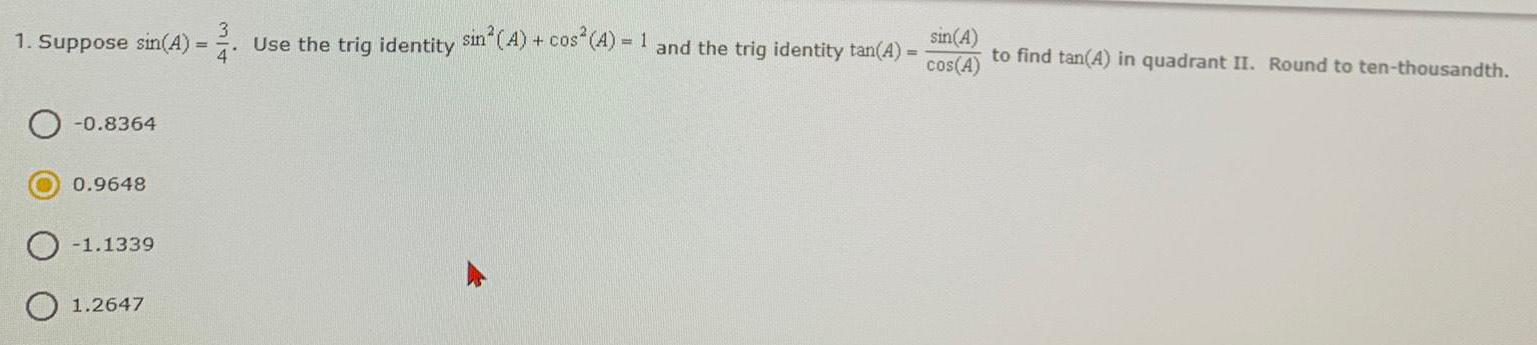
Trigonometry1. Suppose sin(A) = 3/4 Use the trig identity sin² (A) + cos² (A) = 1 and the trig identity tan(A) = sin(A)/cos(A) to find tan(A) in quadrant II. Round to ten-thousandth.
-0.8364
0.9648
-1.1339
1.2647

Math
TrigonometryFind values of the trigonometric functions of the angle (in standard position) whose terminal side passes through the given point.
(21,72)
sin (= (Type an exact answer in simplified form.)
cos (= (Type an exact answer in simplified form.)
tan 0 = (Type an exact answer in simplified form.)
cot 0 = (Type an exact answer in simplified form.)
sec = (Type an exact answer in simplified form.)
CSC = (Type an exact answer in simplified form.)
Math
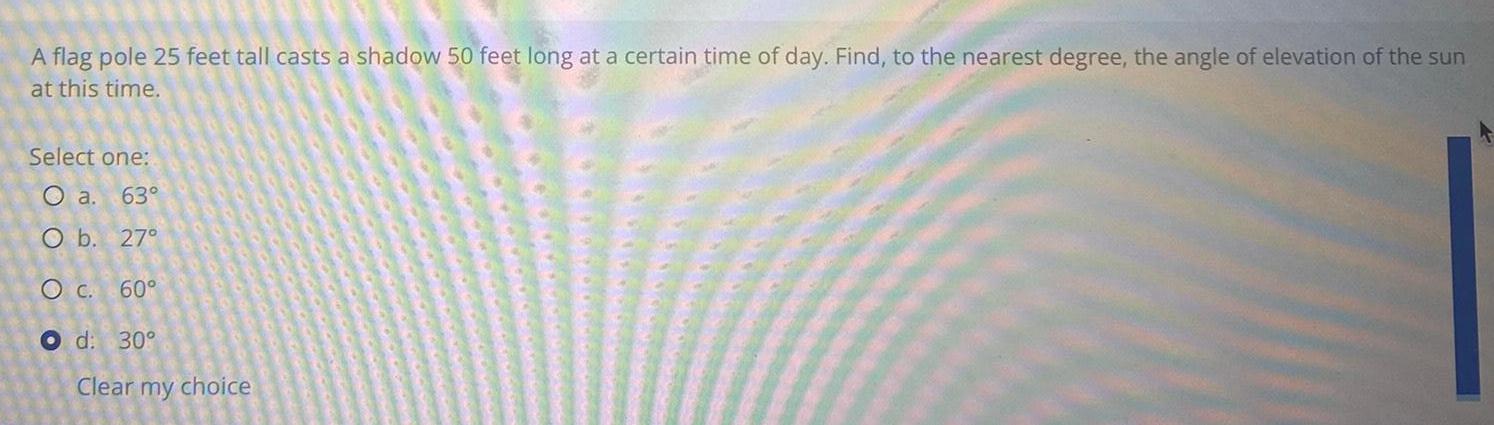
TrigonometryA flag pole 25 feet tall casts a shadow 50 feet long at a certain time of day. Find, to the nearest degree, the angle of elevation of the sun at this time.
Select one:
a. 63°
b. 27°
c. 60°
d: 30°
Clear my choice
Math
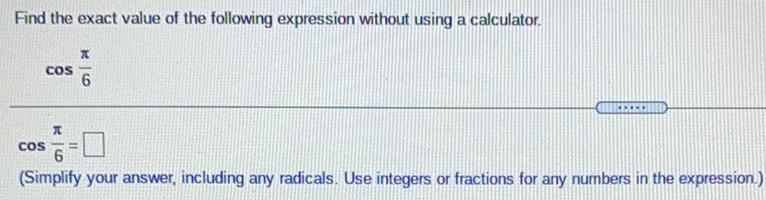
TrigonometryFind the exact value of the following expression without using a calculator.
COS x/6
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
COS x/6

Math
TrigonometryOn separate sets of axes, graph each of the following equations. If you do not remember any shortcuts for graphing, you can always make an x→y table.
a. y=-2x +7
b. y = 3/5x + 1
c. 3x + 2y = 6
d. y = x²
![Verify which of the following are trigonometric identities.
1) 1 + cos² θ / [cot²θ (1-sin²θ)]= 12 sec² θ
2) 18 cos θ[(1/ cos θ)-(cotθ/cscθ)]=18 sin² θ
Both the equations are identities.
Only the second equation is an identity.
Only the first equation is an identity.
None of the equations are identities.](https://media.kunduz.com/media/sug-question/raw/55569895-1658084216.0662737.jpeg?w=256)
Math
TrigonometryVerify which of the following are trigonometric identities.
1) 1 + cos² θ / [cot²θ (1-sin²θ)]= 12 sec² θ
2) 18 cos θ[(1/ cos θ)-(cotθ/cscθ)]=18 sin² θ
Both the equations are identities.
Only the second equation is an identity.
Only the first equation is an identity.
None of the equations are identities.
Math
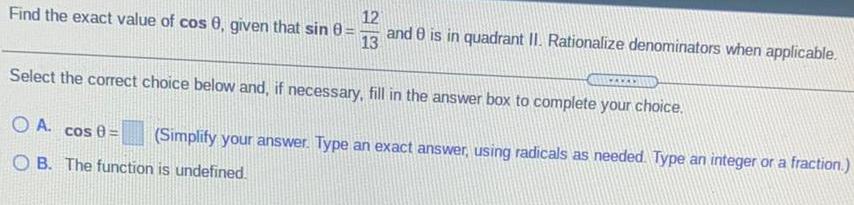
TrigonometryFind the exact value of cosθ , given that sin θ=12/13 and θ is in quadrant II. Rationalize denominators when applicable.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. cos θ= (Simplify your answer. Type an exact answer, using radicals as needed. Type an integer or a fraction.)
B. The function is undefined.

Math
TrigonometryFind all solutions of the trigonometric equation.
2 cos (t) =1
(Give your answer in the form of a comma-separated list if needed. Express numbers in exact form. Use symbolic notation and fractions where needed. Use k to represent any integer.)

Math
TrigonometryThe shadow of a vertical tower is 65.0 ft long when the angle of elevation of the sun is 30.0°. Find the height of the tower.
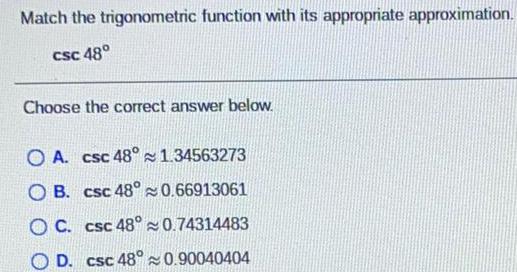
Math
TrigonometryMatch the trigonometric function with its appropriate approximation.
csc 48°
Choose the correct answer below.
A. csc 48° 1.34563273
B. csc 48° 0.66913061
C. csc 48°~0.74314483
D. csc 48° 0.90040404

Math
TrigonometryA rectangular pièce of plywood 5.00 ft by 9.00 ft is cut from one corner to an opposite corner. What are the angles between the edges of the resulting pieces? Include all
resulting angles.
The angle(s) is/are degrees.

Math
TrigonometryFind exact values of the six trigonometric functions of each angle. Rationalize denomi-
nators when applicable. See Examples 2, 3, and 5.
19. 300°
20. 315°
21. 405°
22. 420°
25. 570°
26. 750°
27. 1305° 28. 1500°
31. -510° 32. -1020° 33. -1290° 34. -855°
23. 480°
24. 495°
29. -300° 30. -390°
35.-1860° 36. -2205°

Math
TrigonometryWrite the expression as the cosine of an angle, knowing that the expression is the right side of the formula for cos (α - β) with particular values for α and β.
cos (160°) cos (40°) + sin (160°) sin (40°)
cos (210°)
cos (190°)
cos (220°)
cos (120°)

Math
TrigonometryA country's population and the growth rate in 2011 are given below. Use this information and an exponential model to estimate the country's population in the specified year.
population=142 million; growth rate=1.724 percent year, 2019 million
The size of the population in the 2019 will be about
(Round to the nearest hundredth as needed.)

Math
TrigonometryFind all solutions of the equation in the interval [0, 21).
2 sin ²x + 3 sin x-2=0
Write your answer in radians in terms of T.
If there is more than one solution, separate them with commas.

Math
TrigonometryAssume s is an angle with sin (s) = 2/9, t is an angle with cos (t) = 2/3, and both angles are between 0 and information, together with appropriate identities, to calculate tan (s - t).

Math
TrigonometryFind an approximate value of each expression correct to at least five decimal places if it is defined, otherwise, input undefined.
(a) tan⁻¹ 1.53 = radians.
(b) sin⁻¹ 1.53 = radians.

Math
TrigonometryFor θ=5π/3, explain
a how to draw in standard position
b. how to find the reference angle for, 0
c. how to use the reference angle to evaluate, cos (θ)
without a calculator
Explain in detail, as you would explain to someone who doesn't know any trigonometry. If you are using notation that I never used in class, you must explain what it means.

Math
TrigonometryFrom a hot air balloon, the angle between a radio antenna straight below and the base of the library downtown is 57°, as shown below. If the distance between the radio antenna and the library is 1.3 miles, how many miles high is the balloon?
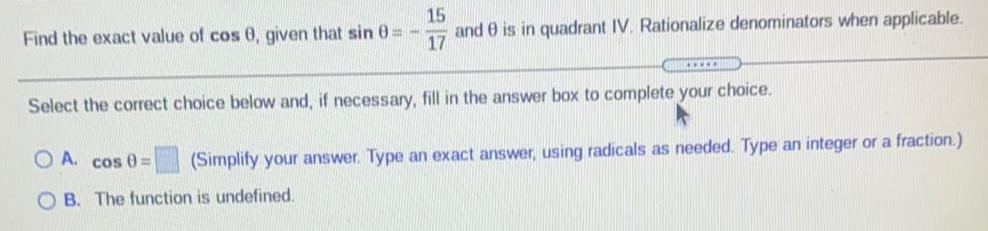
Math
Trigonometry1Find the exact value of cos 0, given that sin θ= -15/17 and θ is in quadrant IV. Rationalize denominators when applicable.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. cos θ =
B. The function is undefined.

Math
TrigonometrySolve triangle ABC if ZA = 43.1°, a = 183.6, and b = 243.4.
sin B
(round answer to 5 decimal places)
There are two possible angles B between 0° and 180° with this value for sine. Find the two angles,
and report them so that B₁ is the acute angle.
LB₁ =
and B₂
(round these and all remaining answers to 2 decimal places)
Thus, two triangles satisfy the given conditions: triangle A₁B₁C₁ and triangle A2 B2C2-
Solve the first triangle: A₁B₁C₁
ZC1
and C1
=
=
Solve the second triangle: A2 B2C2
ZC₂
and C2 =
=
=

Math
TrigonometryGiven the equation y
-
The amplitude is:
The period is:
The horizontal shift is:
The midline is: y =
4 sin
3π
4
x +
15TT
4
+6
units to the Select an answer
Select an answer
Left
Right


Math
TrigonometryA man looks to the top of a hill and finds the angle of elevation to be 50°10'. He then moves 40 feet away from the hill and finds the angle of elevation to be 42°20'. Find the height of the hill.

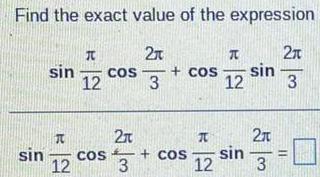

Math
TrigonometryUse a double-angle formula to find the exact value of the given expression.
2 cos²105° -1

Math
TrigonometryWhich of the following is equivalent to tanθ cscθ cotθ for all values of θ for which tanθ cscθ cotθ is defined?
Select the correct answer below:
sinθ
tanθ
cot θ
cscθ
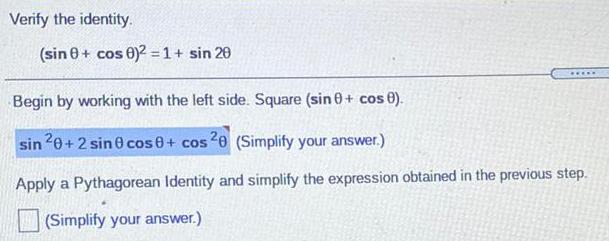

Math
TrigonometryUse the cosine of a sum and cosine of a difference identities to find cos (s+t) and cos (s-t).
sin s=12/13 and sint=-4/5 s in quadrant II and t in quadrant IV
cos (s+t) =
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
cos (s-t)=
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
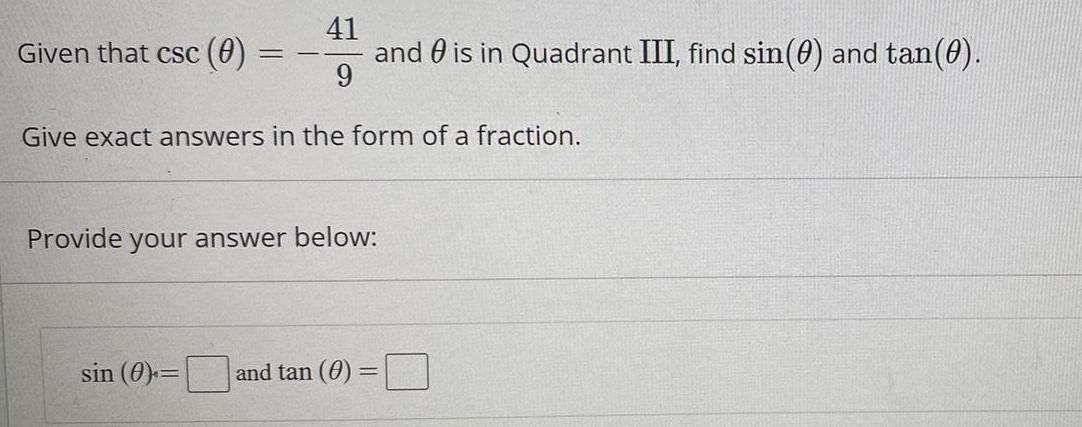
Math
TrigonometryGiven that csc (θ) = -41/9 and θ is in Quadrant III, find sin(θ) and tan(θ).
Give exact answers in the form of a fraction.

Math
TrigonometryA 20-foot support post leans against a wall, making a
70° angle with the ground. To the nearest tenth of a
foot, how far up the wall will the support post reach?
A) 68 B) 6.9 C) 18.7 D) 18.8

Math
TrigonometryA drone is flying over a college campus. The drone spots the cafeteria on the west end of campus at a 34° angle
of depression. If the cafeteria and sports complex are separated by a straight road 2.3 mi long, how high is the
drone?
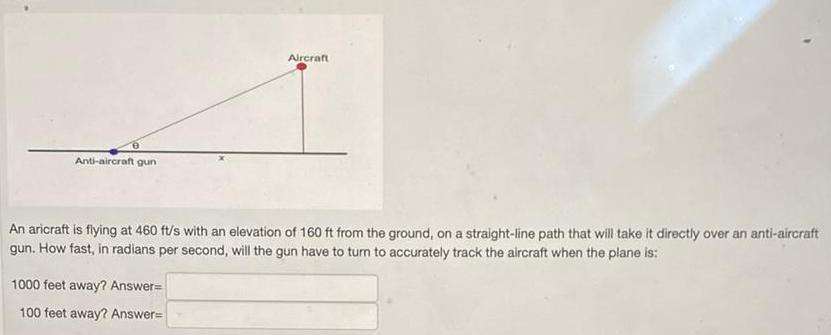
Math
TrigonometryAnti-aircraft gun
Aircraft
An aricraft is flying at 460 ft/s with an elevation of 160 ft from the ground, on a straight-line path that will take it directly over an anti-aircraft
gun. How fast, in radians per second, will the gun have to turn to accurately track the aircraft when the plane is:
1000 feet away? Answer=
100 feet away? Answer=

Math
TrigonometryGiven a right triangle with sin(θ) = 6/11, determine the value of the other trigonometric ratios of θ.
1. cos(θ)
2 tan(θ)=
3. sec(θ)
4. csc (θ) =
5. cot(θ)=
Use exact notation, no decimal approximations.
If you need to write a number such as √3, type out sqrt(3).
![For each angle (in radians) below, determine the quadrant in which the terminal side of the angle is found.
[NOTE: Enter '1' for quadrant I, '2' for quadrant II, '3' for quadrant III, and '4' for quadrant IV.]
(a) 0 = 5 is found in quadrant
3
(b) 0 = 3 is found in quadrant
(c) 0 = 17 is found in quadrant
6
(d) 0 = 5 is found in quadrant
I
A](https://media.kunduz.com/media/sug-question/raw/59241788-1657876126.1791654.jpeg?w=256)
Math
TrigonometryFor each angle (in radians) below, determine the quadrant in which the terminal side of the angle is found.
[NOTE: Enter '1' for quadrant I, '2' for quadrant II, '3' for quadrant III, and '4' for quadrant IV.]
(a) 0 = 5 is found in quadrant
3
(b) 0 = 3 is found in quadrant
(c) 0 = 17 is found in quadrant
6
(d) 0 = 5 is found in quadrant
I
A

Math
TrigonometryConsider the function y = 3 cos
8
In the "Show Work" area:
(a) Determine the amplitude and period.
(b) Using by-hand techniques, determine the 5 key points of the first cycle.
(c) Sketch exactly 2 full cycles of the function.

Math
TrigonometryFor a project in his Geometry class, Ajay uses a mirror on the ground to measure the height of his school's football goalpost. He walks a distance of 8.85 meters from the goalpost, then places a mirror on flat on the ground, marked with an X at the center. He then steps 4.6 meters to the other side of the mirror, until he can see the top of the goalpost clearly marked in the X. His partner measures the distance from his eyes to the ground to be 1.15 meters. How tall is the goalpost? Round your answer to the nearest hundredth of a meter.
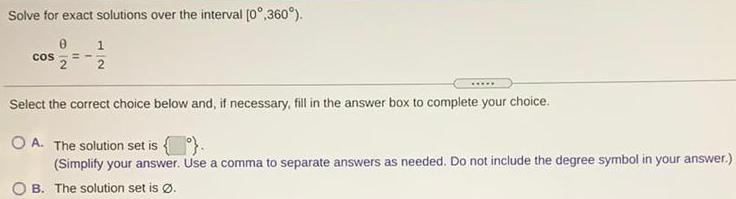
Math
TrigonometrySolve for exact solutions over the interval [0°,360°).
cos θ/2 = -1/2
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Simplify your answer. Use a comma to separate answers as needed. Do not include the degree symbol in your answer.)
B. The solution set is Ø.
Math
Trigonometry3
A 25-foot water slide has a 10.8-ft ladder which meets the slide at a 100° angle. To the nearest tenth, what is the distance between the end of the slide
and the bottom of the ladder?
• Write your answer as a number only.
• Round answer to one decimal place.
Answer
Answer

Math
Trigonometry5
Two observers are 2.4 miles apart on opposite sides of a hot-air balloon. The angle of elevation from observer A is 30° and the angle of elevation from
observer B is 35°. Find the alitude of the balloon to the nearest tenth of a mile.
Write your answer as a number only.
. Round answer to one decimal place.
B
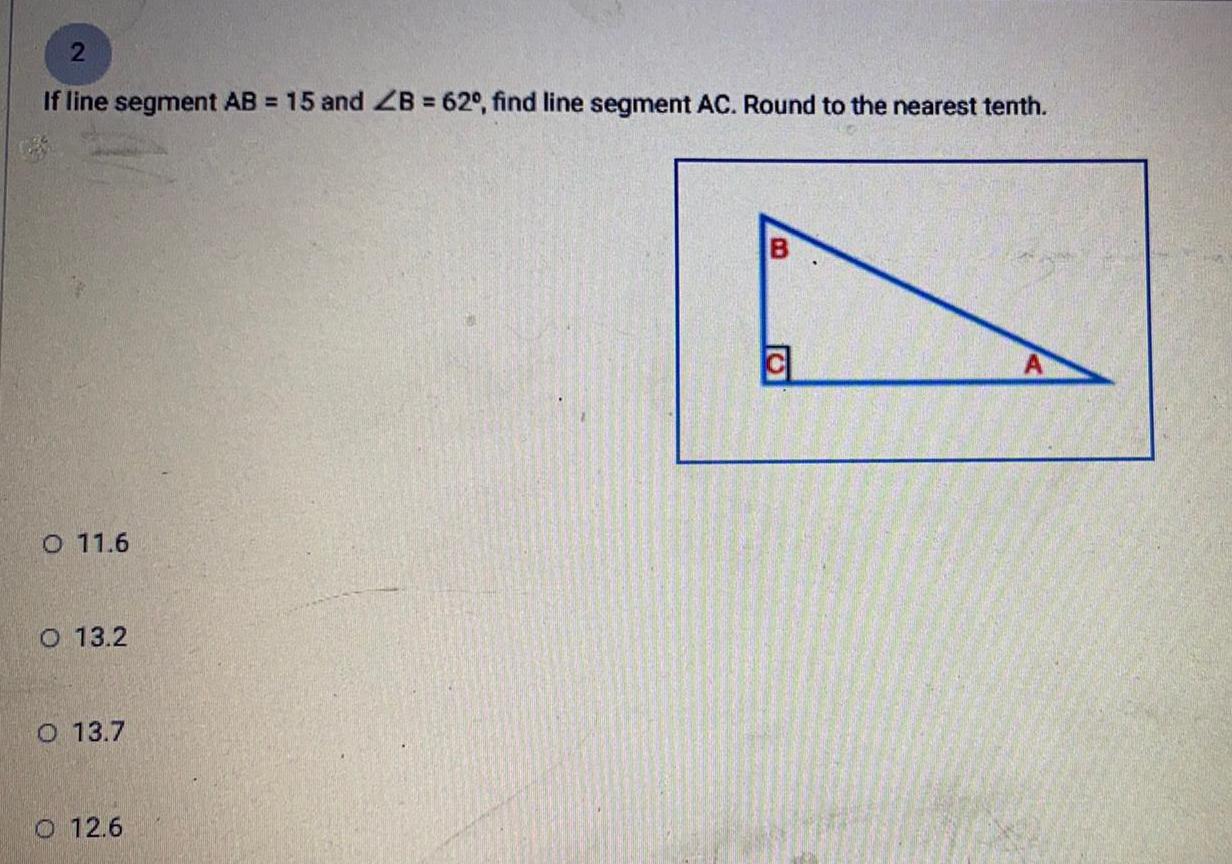
Math
TrigonometryIf line segment AB = 15 and ∠B = 62°, find line segment AC. Round to the nearest tenth.
11.6
13.2
13.7
12.6

Math
TrigonometryUse the law of sines to solve the given problem.
The loading ramp at a delivery service is 11.5 ft long and makes a 20.0° angle with the horizontal. If it is replaced with a ramp 21.5 ft long, what angle does the new ramp
make with the horizontal?
The new ramp makes a
(Round to one decimal place as needed.)
angle with the horizontal.

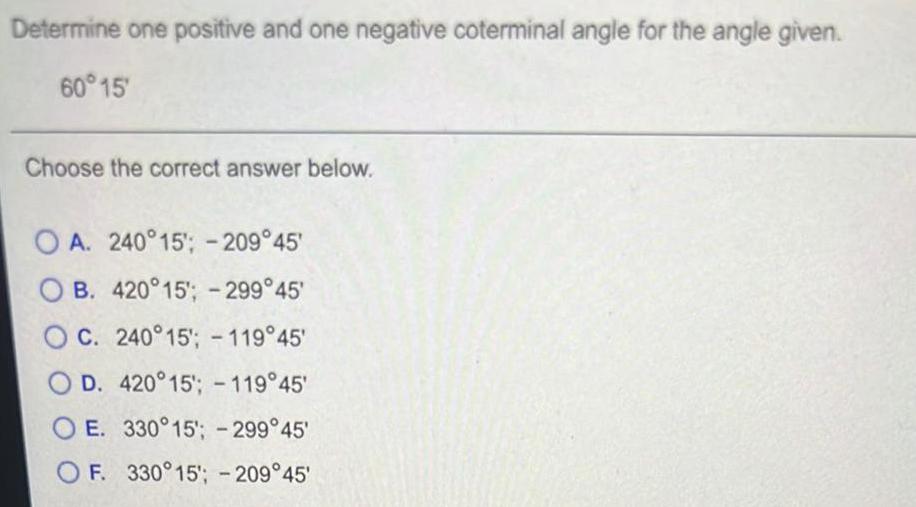
Math
TrigonometryDetermine one positive and one negative coterminal angle for the angle given.
60° 15'
Choose the correct answer below.
A. 240°15'; -209°45'
B. 420°15'; -299°45'
C. 240°15'; -119°45'
D. 420°15'; -119°45'
E. 330°15'; -299°45'
F. 330°15'; - 209°45'
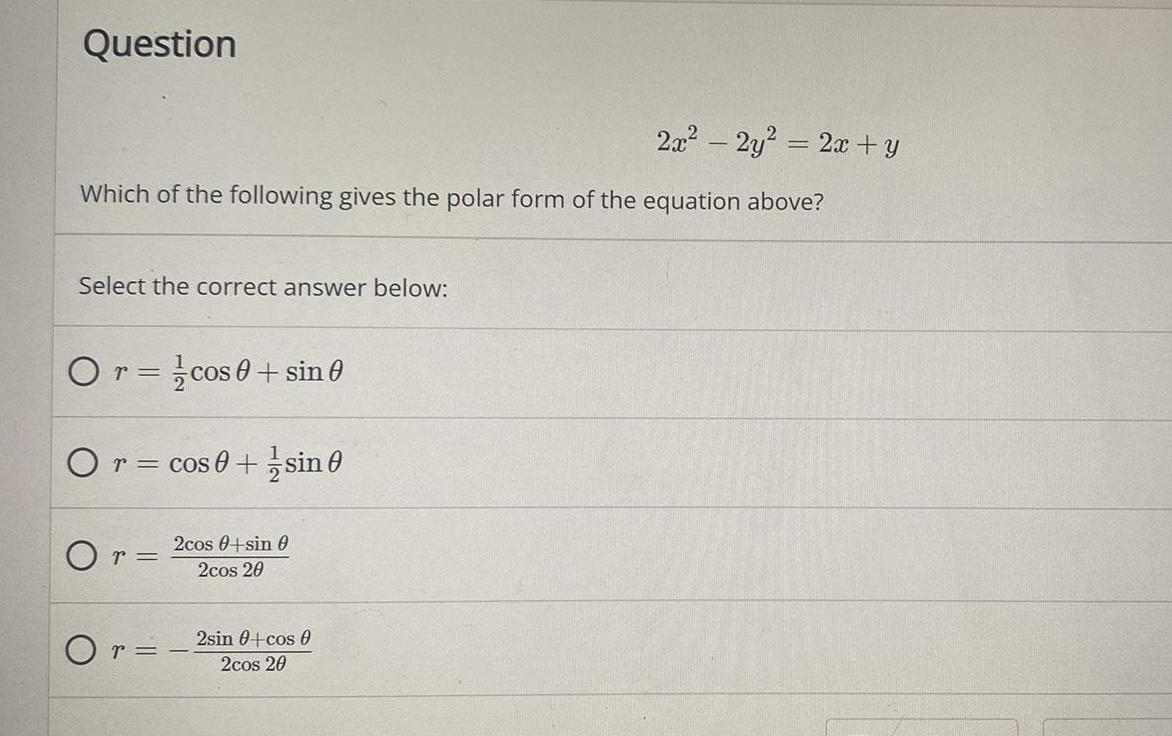
Math
Trigonometry2x2 - 2y2 = 2x + y
Which of the following gives the polar form of the equation above?
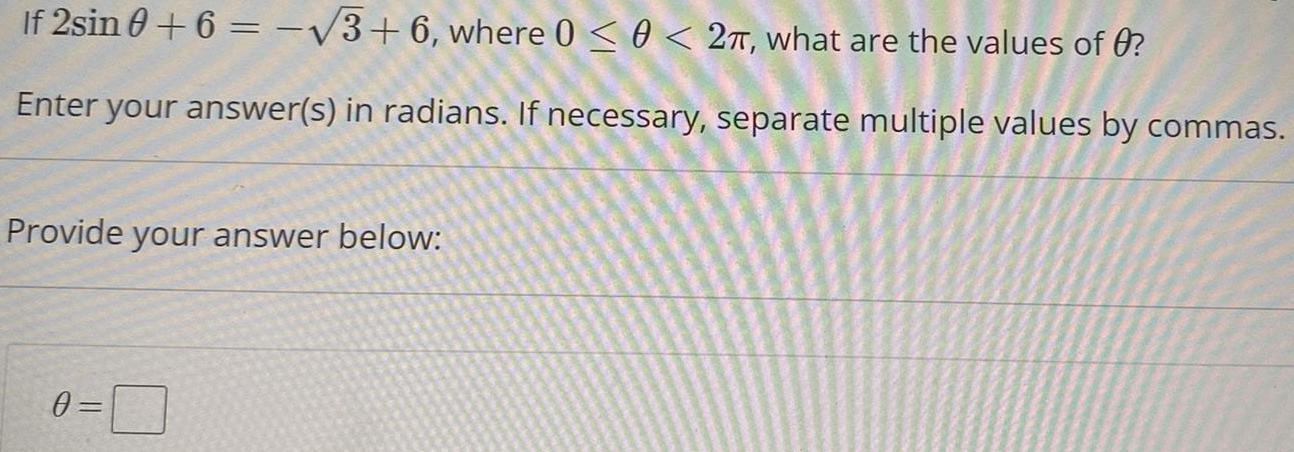
Math
TrigonometryIf 2sinθ+ 6 = -√3+6, where 0 ≤ θ < 2π, what are the values of θ?
Enter your answer(s) in radians. If necessary, separate multiple values by commas.
Provide your answer below:
θ =
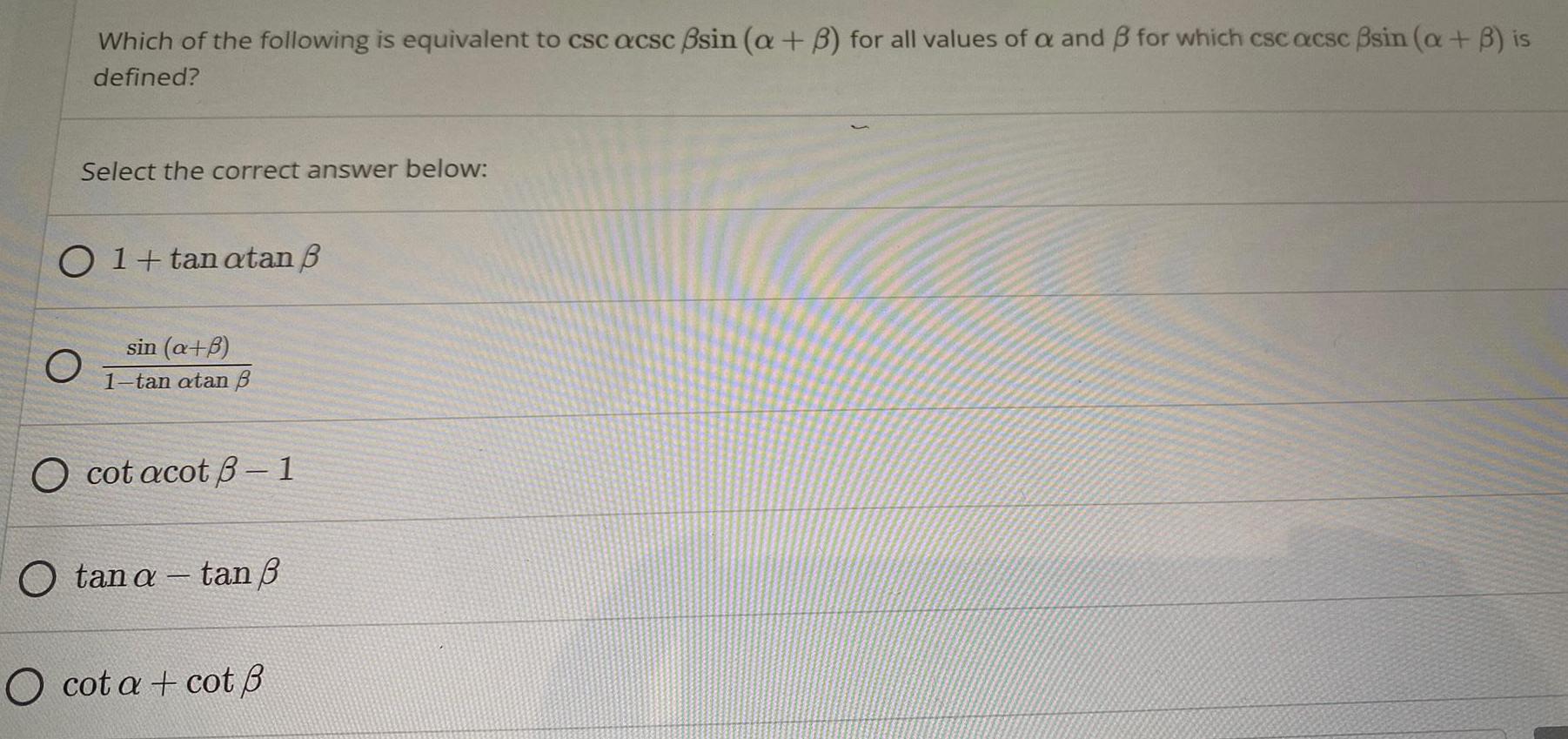
Math
TrigonometryWhich of the following is equivalent to csc acsc ßsin (a + B) for all values of a and B for which csc acsc ßsin (a + B) is defined?
Select the correct answer below:
1+tan atan β
sin (α+b)/(1-tan αtanβ)
cotαcot β-1
tanα- tan v
cotα+cot β