Probability Questions and Answers

Math
ProbabilityTeams of students compete in a robotics contest. The times for the robots to complete an obstacle course are normally distributed. The mean time for completion is 60 seconds, and the standard deviation is 4 seconds. Approximately what percentage of the robots will complete the course in 56 to 64 seconds?
A. 68%
B. 60%
C.50%
D 8%

Math
ProbabilitySuppose there is a 22.1% probability that a randomly selected person aged 30 years or older is a jogger. In addition, there is a 25.8% probability that a randomly selected person aged 30 years or older is male, given that he or she jogs. What is the probability that a randomly selected person aged 30 years or older is male and jogs? Would it be unusual to randomly select a person aged 30 years or older who is male and jogs?
The probability that a randomly selected person aged 30 years or older is male and jogs is 0.057 (Round to three decimal places as needed.).
Would it be unusual?
Yes
No
No

Math
ProbabilityAt Andrew Jackson High School, students are only allowed to enroll in AP U.S. History if they have already taken AP World History or AP European History. Out of 825 incoming seniors, 165 took AP World History, 66 took AP European History, and out of those students 33 took both. Given this information, determine the probability a randomly selected incoming senior is allowed to enroll in AP U.S. History.

Math
ProbabilityFor the month of August in a certain city, 57% of the days are cloudy. Also in the month of August in the same city, 19% of the days are cloudy and snowy. What is the probability that a randomly selected day in August will be snowy if it is cloudy?
The probability is approximately. (Round to three decimal places as needed.)

Math
ProbabilityA yogurt shop offers 25 flavors of frozen yogurt. Evie randomly chooses 3 different flavors for her banana split. What is the probability she chooses chocolate, vanilla, and strawberry? (Independent and Dependent Events)

Math
ProbabilityOut of 75 students, 45 are taking Algebra 2 and 32 are taking Chemistry. Sixteen students are taking both Algebra 2 and Chemistry. If a student is chosen at random, what is the probability that the student is taking Algebra 2 but not Chemistry?

Math
ProbabilityEvery day, Carmen walks to the bus stop and the amount of time she will have to wait for the bus is between 0 and 12 minutes, with all times being equally likely (i.e., a uniform distribution). This means that the mean wait time is 6 minutes, with a variance of 12 minutes.
What is the probability that her total wait time over the course of 60 days is less than 6.5 hours?

Math
ProbabilityMs. Kelly is organizing a board game day. She has 7 different board games. She needs to organize the order that the games are played that day.
S={Apples To Apples, Balderdash, Carcassonne, Dominion, Terraforming Mars,
Wingspan, Galaxy Trucker}
a) In how many ways can she play all 7 games?
b) In how many ways can she play just 3 of the games?
c) In how many ways can she play just 3 games if the last one must be Terraforming
Mars because that's everyone's favourite?
d) In how many ways can she play just 3 games if Terraforming Mars must be played at some point that day because that's everyone's favourite?
e) Apple to Apples and Balderdash are both considered "party" games, in how many
ways can all the games be played if Apples to Apples and Balderdash are not played
one right after the other?

Math
ProbabilityChoose one of the following questions to answer
Level 4-
A new supermarket was launched in Kitchener. On opening day customers came to the store and were asked how they heard about the grand opening. They were informed via the following methods:
- 119 received flyers in the mail
- 131 learned about the launch through the internet
- 140 heard about the launch through advertisements on television
- 41 were aware of the launch through flyers and the internet
- 35 came to know of it through flyers and television
- 16 heard about it from all three sources
a) Construct a Venn diagram.
b) Calculate n(S), what does that mean in the context of this question?
c) Calculate n(F ∪ T), what does that mean in the context of this question?
Level+4
A survey collects data from people about what pets they like. The choices were cats, dogs, and birds. The results were as follows:
- 95 like cats
- 165 like dogs
-93 like birds
- 75 like cats and dogs
-20 like dogs and birds
- 18 like cats and birds
-10 like none of those choices
There are 265 people surveyed
a) Construct a Venn diagram.
b) Calculate n(D ∩ C ∩ B), what does that mean in the context of this question?
c) Calculate n(C'), what does that mean in the context of this question?

Math
ProbabilityDetermine whether each of the following probabilities is either theoretical or empirical.
You played blackjack and had one blackjack out of 10 times. Then your probability of getting a blackjack is
1/10 = 10%
The probability of blackjack from the first two cards is
32/663 ≈ 4.8%
1. Theoretical probability 2. Relative frequency

Math
ProbabilitySuppose there is a 12.6% probability that a randomly selected person aged 20 years or older is a jogger. In addition, there is a 18.5% probability that a randomly selected person aged 20 years or older is female, given that he or she jogs. What is the probability that a randomly selected person aged 20 years or older is female and jogs? Would it be unusual to randomly select a person aged 20 years or older who is female and jogs?

Math
ProbabilityA survey of 78 men and women was conducted. Of the 78 surveyed, 41 were women, 28 were married, and 17 were married women. What is the probability of randomly selecting a woman or someone married? (Hint: Draw a Venn diagram)
a. 52/78
b. 69/78
c. 41/78
d. 28/78

Math
ProbabilityThe amount of money that a car insurance company pays out in a given week on single-car accidents follows approximately a normal distribution with mean $45,000 and a standard deviation of $10,000.
What is the probability that the insurance company will have to pay out more than $60,000 in a given week?
0.067
0.111
0.413
0.933

Math
ProbabilityUse technology to find the P-value for the hypothesis test described below. The claim is that for 12 AM body temperatures, the mean is u> 98.6°F. The sample size is n=3 and the test statistic is t= 1.013. (Round to three decimal places as needed.) P-value=

Math
ProbabilityUse the Fundamental Counting Principle to determine the total number of outcomes.
3. Picking a card from a standard deck then rolling a standard die.
4. Choosing a random answer to the last five questions on a multiple-
choice test if each question has four answer choices.
5. A mall has four escalators, one elevator, and three stairwells to
travel from the second floor to the first floor. They have six doors on
the first floor to exit the mall. If Jane is on the second floor, how
many ways can she exit the mall?

Math
ProbabilityAlex is taking two courses; algebra and history. Student records indicate that the probability of passing algebra is 0.55, that of passing history is 0.4, and that of passing at least one of the two courses is 0.7. Find the probability that Alex will pass both courses. • Write the probability as a decimal For example, 0.22
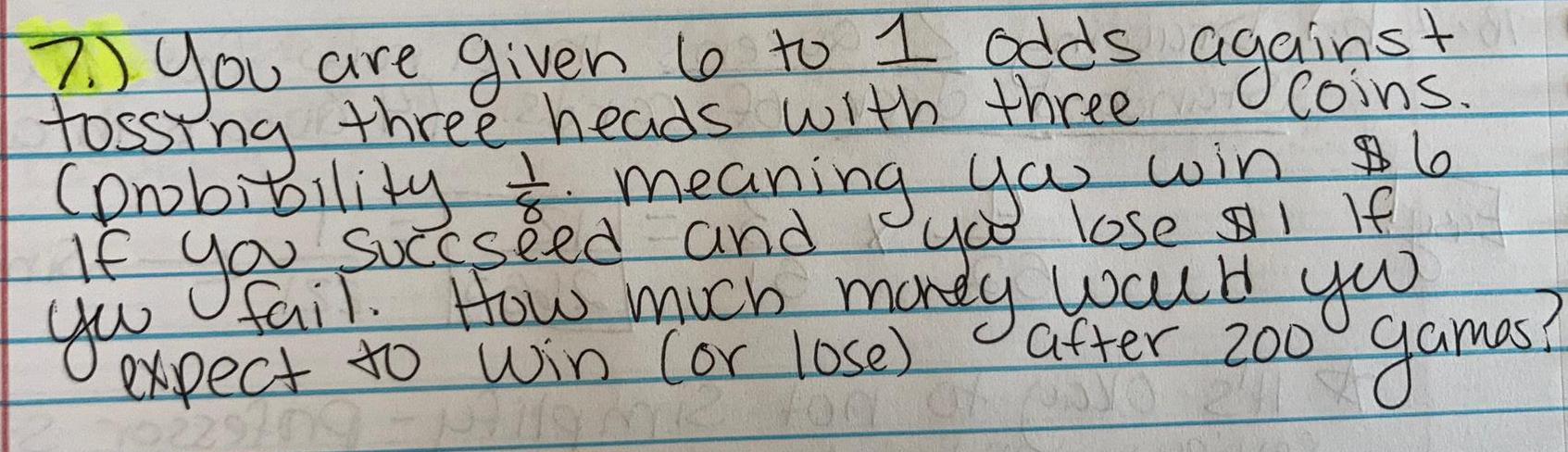
Math
ProbabilityYou are given 6 to 1 odds against tossing three heads with three coins . (probability 1/8 meaning you win $ 6 if you succeed and you lose $ 1 if you fail. How much money you expect to win (or lose) after 200 games?

Math
ProbabilitySelect ALL the correct answers.
Two friends worked together on an entry for a poetry contest and won; however, there is only one prize and it cannot be split. Some methods of determining who receives the prize are given below.
Select all the fair methods for determining who receives the prize.
ask a stranger to flip a coin
throw a stone closest to an object place both names in equal amounts into a hat and draw one without looking
ask a random friend to choose
roll a die and evaluate the outcome as either even or odd
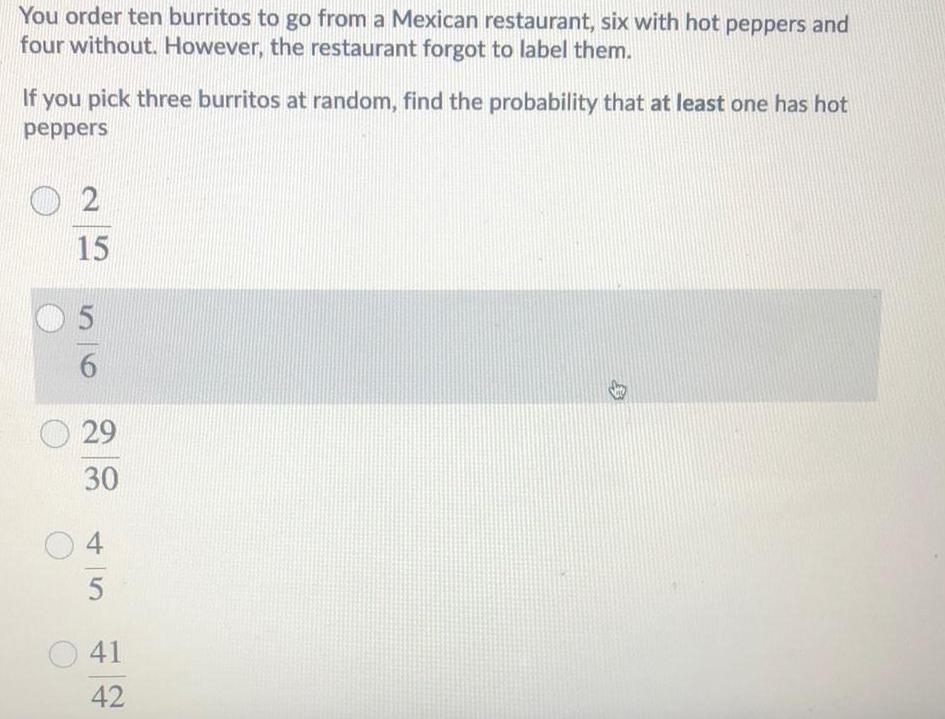
Math
ProbabilityYou order ten burritos to go from a Mexican restaurant, six with hot peppers and
four without. However, the restaurant forgot to label them.
If you pick three burritos at random, find the probability that at least one has hot
peppers
2/15
5/6
29/30
4/5
41/42

Math
ProbabilityAccording to a recent survey, forty percent of the people living in a certain region carry a certain genetic trait. People from the region will be selected at random one at a time until someone is found who carries the genetic trait. Let the random variable X represent the number of people selected to find one person who carries the genetic trait. On average, how many people from the region will need to be selected to find one person who carries the genetic trait?

Math
ProbabilityNell donated 30 notebooks to a local school and Ronald donated 20 notebooks. Of the donated notebooks, 16 of Neil's notebooks were wide-ruled and 12 of Ronald's notebooks were wide-ruled.
Charmaine will randomly choose a notebook from a box containing either Neil's or Ronald's donated notebooks. If she wants to pick a wide-ruled notebook, which box should she choose from?
A. Charmaine is equally likely to choose a wide-ruled notebook from Ronald's box or Neil's box.
B. There is not enough information to determine whose box Charmaine should choose.
C. Neil's box
D. Ronald's box

Math
ProbabilityIn a recent study on world happiness, participants were asked to evaluate their current lives on a scale from 0 to 10, where 0 represents the worst possible life and 10 represents the best possible life. The responses were normally distributed, with a mean of 5.4 and a standard deviation of 1.8. Answer parts (a)-(d) below.
(a) Find the probability that a randomly selected study participant's response was less than 4.
The probability that a randomly selected study participant's response was less than 4 is. (Round to four decimal places as needed.)

Math
ProbabilityUniversity of Tennessee Volunteers women's basketball team. She has injured her ankle, and it is doubtful that she will be able to play in an upcoming game/If Candace can play the coach estimates that the Volunteers will score 78 points. If she is unable to play, the coach estimates that the team will Score 62 points. The team doctor estimates there is a 50% chance Candace will play. Determine the number of points the team can expect to score.

Math
ProbabilityA pair of dice is rolled.
What is the probability that the sum is 3, given that the sum is odd?
Write a fraction in simplest form
For example, 12/17

Math
Probability19% of all college students volunteer their time. Is the percentage of college students who are
volunteers different for students receiving financial aid? Of the 350 randomly selected students who
receive financial aid, 53 of them volunteered their time. What can be concluded at the a = 0.10 level of significance? Write hypothesis, give test stat and p-value. Write conclusions about HO and claim.
Select the correct conclusion below:
a) Students who receive financial aid volunteer as much as the other students.
b) Students who receive financial aid does not volunteer at the same rate as other students,

Math
ProbabilityA bag has 2 red balls, 4 blue balls, and 3 yellow balls. Two balls are taken out of the bag 1 at a time. Is each statement True or False?
A The probability of drawing 2 blue balls is 1/3.
True False
B If the first ball drawn is red, the probability that the second ball is also red is 1/36.
True False
C The probability of drawing a blue ball and then a red ball is 1/9.
True False

Math
ProbabilityThe probability that Gary and Jane have a child with blue eyes is 0.4, and the probability that they have a child with blond hair is 0. 25. The probability that they have a child with both blue eyes and blond hair is 0. 1. Given this information, the events blue eyes and blond hair are 1: dependent
II: independent
III: mutually exclusive
(A) I, only
(B) II, only
(C) I and III
(D) II and III

Math
ProbabilityIn the game of roulette, a player can place a $10 bet on the number 7 and have a 1/38 probability of winning. If the metal ball lands on 7, the player gets to keep the $10 paid to play the game and the player is awarded an additional $350. Otherwise, the player is awarded nothing and the casino takes the player's $10. Find the expected value E(x) to the player for one play of the game. If x is the gain to a player in a game of chance, then E(x) is usually negative. This value gives the average amount per game the player can expect to lose.
The expected value is $
(Round to the nearest cent as needed.)

Math
ProbabilityA survey of TV viewing habits of 50 men and 50 women found the following information: Of the 50 men, 20 prefer watching baseball and 30 prefer football. Of the 50 women, 25 prefer watching baseball and 25 prefer football. Construct a data table
for this data and answer this question: Out of the entire survey, what is the probability of choosing a man who prefers
football?
1/5
3/10
2/5
1/2

Math
ProbabilityYou spin a spinner that is equally divided into 9 parts. 3 parts are green, 2 parts are speckled, 2 parts are yellow, and 2 parts are black. What is the probability of the spinner stopping at a red section? Write your answer as a fraction.

Math
ProbabilityDetermine the probability of choosing a month that starts with a vowel or a month that is represented by an even number. Determine if these are independent events or mutually exclusive events and then show all of your work with the formula you use.

Math
ProbabilityTwo marbles are to be pulled from a bag that contains 2 yellow marbles, 4 green marbles, and 6 orange marbles. After the first marble is drawn, it is not replaced. What is the probability that two orange marbles are chosen from the bag?
1/2
5/24
11/12
5/22
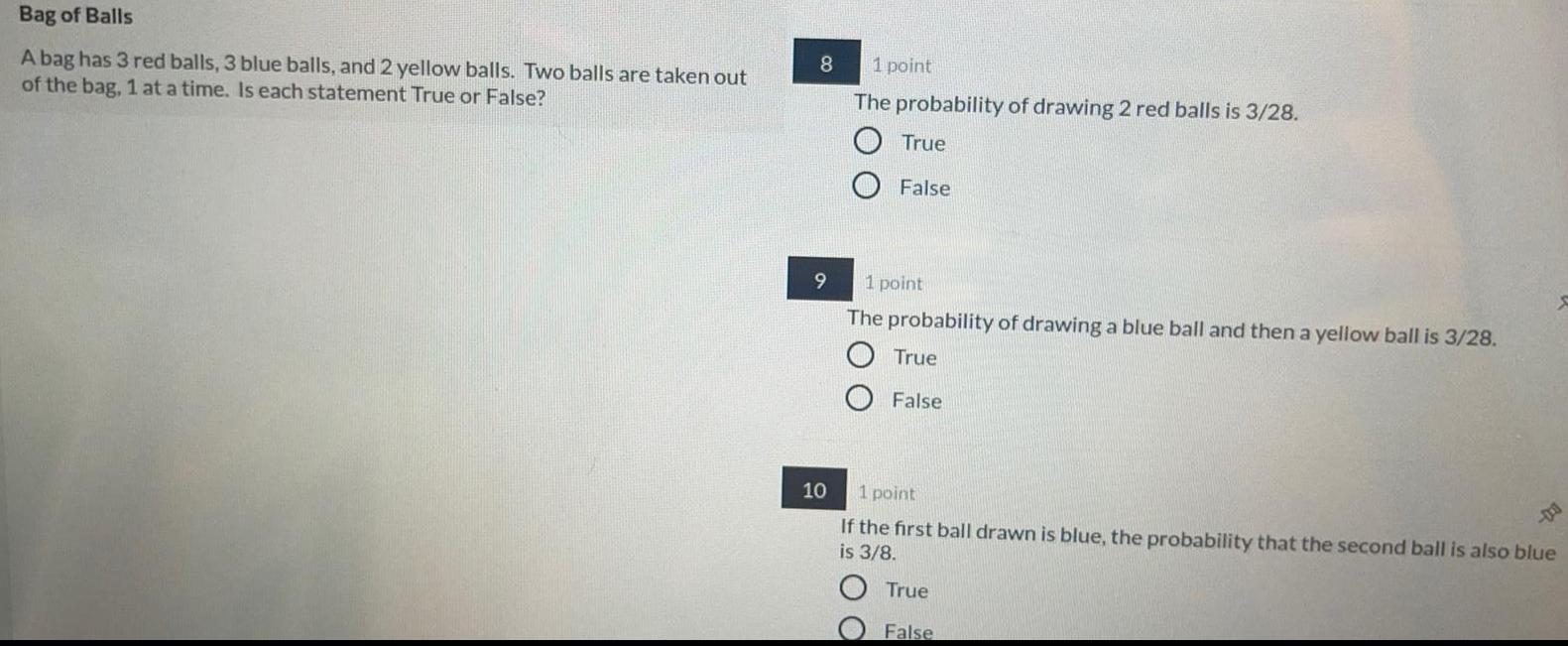
Math
ProbabilityA bag has 3 red balls, 3 blue balls, and 2 yellow balls. Two balls are taken out
of the bag, 1 at a time. Is each statement True or False?
The probability of drawing 2 red balls is 3/28.
True
False
The probability of drawing a blue ball and then a yellow ball is 3/28.
True
False
If the first ball drawn is blue, the probability that the second ball is also blue
is 3/8.

Math
ProbabilityExplain the difference between finding P(A or B) and P(A and B). Suppose A and B are dependent events. Provide an example for each probability.

Math
ProbabilityConstruct a normal bell curve with the mean, the deviations from the mean, and the percentages of the three areas under the curve. Upload the image for your teacher to grade.

Math
ProbabilityA researcher found a Person correlation, r=-0.42 between frequency of binge drinking and GPA in
a sample of n = 29 undergraduate students. With the 2-tails test, he should conclude that
there is a significant negative relationship between these variables with p <.05 but not with p <.01.
there is a significant negative relationship between these variables with p <.01 but not with p <.05.
there is a significant negative relationship between these variables with either, p <.05 or p <.01
there is no significant relationship between these variables with neither, p <.05 nor p <.01

Math
ProbabilityExactly 62% of the teachers in your school are under 47 years old. In addition, 4% of the teachers are over 49 years old. What is the probability that a teacher chosen at random is under 47 or over 49 years old?
62%
72%
66%
58%

Math
ProbabilityThe average life span of one particular brand of refrigerator is 12 years with a standard deviation of 0.8. Find the percentage of refrigerators that last for more than 14 years.
0.62%
6.2%
0.60%
62%

Math
ProbabilityDenis examined the records of the clients who had joined his gym more than six months ago, and he found the following:
P(joined in January) = 0.12
P(member for over 6 months) = 0.5
P(over 6 months and joined in January) = 0.024
Find the probability that a client remained a member for more than 6 months, given that the client joined in January, and write the equation in proper notation.

Math
ProbabilityThree starting youth basketball players are ages 8, 10, and 9. Solve for the probability that a sample of two is randomly chosen.
Show your work and explain the steps you used to solve.

Math
ProbabilityJuan runs a company that makes pens. He notices that 1 out of every 9 pens are faulty. He uses a standard deck of cards to model the situation, with all the 10s representing faulty pens. Which statement about his model is true?
a. His model cannot be improved.
b. His model can be improved the most by removing all the hearts from the deck.
c. His model can be improved the most by removing all face cards from the deck.
d. His model can be improved the most by removing all the face cards and aces from the deck.

Math
Probability37% of adults say cashews are their favorite kind of nut. You randomly select 12 adults and ask each to name his or her favorite nut. Find the probability that the number
who say cashews are their favorite nut is (a) exactly three, (b) at least four, and (c) at most two. If convenient, use technology to find the probabilities.
(a) P(3) (Round to the nearest thousandth as needed.)
(b) P(x≥4)=(Round to the nearest thousandth as needed.)

Math
ProbabilityA 6-sided die is rolled. The set of equally likely outcomes is {1,2,3,4,5,6). Find the probability of rolling a number less than 8.
The probability of rolling a number less than 8 is

Math
ProbabilityIn Ventura County, the height measurements of ten-year-old children are approximately normally distributed with a mean of 54.7 inches, and standard deviation of 5.1 inches. Let X be the height of a randomly chosen child in Ventura County.
a. What is the distribution of X?X - ?
Please show the following answers to 4 decimal places.
b. If a Ventura County child is randomly chosen, find the probability that the height is at least 57.3 inches.
c. If a Ventura County child is randomly chosen, find the probability that the height is between 57.3 and 65 inches.
Please show the following answer to 1 decimal place.

Math
ProbabilityA bag contains 4 red balls, 6 blue balls, and 8 yellow balls. If you replace each ball after you see it's color, find the probability of removing a blue ball, then a red ball, and then a yellow ball. Write your answer as a fraction simplified to lowest terms (reduced).

Math
ProbabilityTotal blood volume in ml per body weight in kg, is important in medical research. For healthy adults, the red blood cell volume is about μ = 28 ml/kg. Suppose Roger has had seven blood tests and the mean red blood cell count was 32.7 ml/kg. Assume that x has a normal distribution and o = 4.75. Do the data indicate that Roger's red blood cell volume is different either way from μ = 28 ml/kg? Use a = 0.01.

Math
ProbabilityThirty percent of consumers prefer to purchase electronics online. You randomly select 8 consumers. Find the probability that the number of consumers who prefer to
purchase electronics online is (a) exactly five, (b) more than five, and (c) at most five.
(a) Find the probability that the number that prefer to purchase electronics online is exactly five.
P(5) =

Math
ProbabilityHow many times would a coin have to show heads in 50 tosses to have an experimental probability of 20% more than the theoretical probability of getting heads?
A. 10
B. 25
C 35
D 45

Math
ProbabilityA restaurant offers a choice of 5 salads, 7 main courses, and 3 desserts. How many possible 3-course meals are there?
A. 210
B. 105
C. 15
D. 35
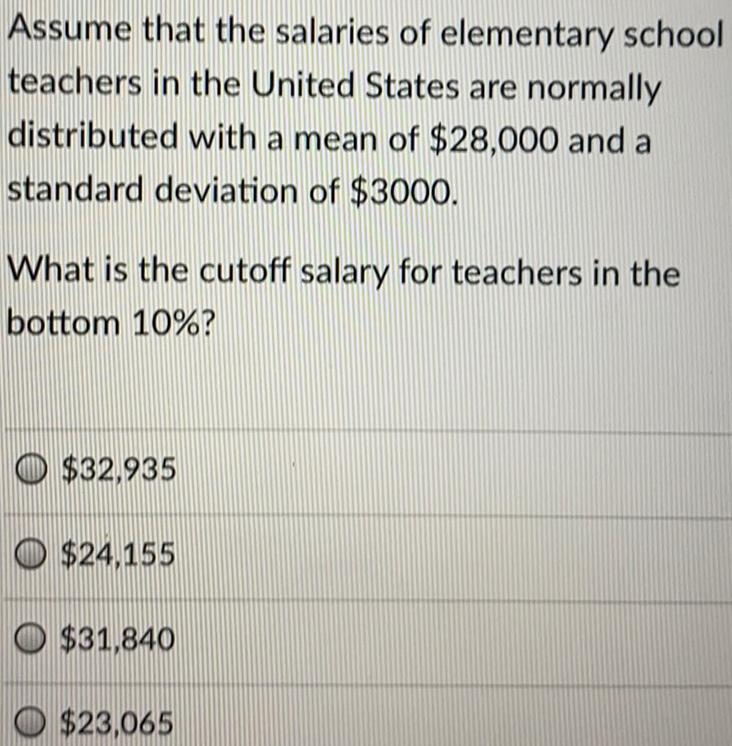
Math
ProbabilityAssume that the salaries of elementary school teachers in the United States are normally distributed with a mean of $28,000 and a standard deviation of $3000. What is the cutoff salary for teachers in the bottom 10%?
$32,935
$24,155
$31,840
$23,065