Probability Questions and Answers

Math
ProbabilityA parachutist drops a penny from 1000 feet above the ground. What is the probability of the penny landing a 10 cm x 10 cm square inside a 1000 cm x 1000 cm square?

Math
Probability27% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she
uses credit cards. Find the probability that the number of college students who say they use credit cards because of the rewards program is (a) exactly two, (b) more
than two,
and (c) between two and five inclusive. If convenient, use technology to find the probabilities.
(a) P(2)= (Round to the nearest thousandth as needed.)
(b) P(x > 2) = (Round to the nearest thousandth as needed.)

Math
ProbabilityEight people in the class are left-handed. If there are 32 students in the class, what is the probability of randomly choosing one who is right-handed?

Math
ProbabilityA warehouse employs 27 workers on first shift, 16 workers on second shift, and 14 workers on third shift. Eight workers are chosen at random to be interviewed about the work environment. Find the probability of choosing exactly two second shift workers and two third shift workers.

Math
ProbabilitySolve the problem involving probabilities with independent events. A card is drawn from a 52-card deck and a fair coin is flipped. What is the probability of getting jack and heads?
1/26
1/13
3/52
1/4

Math
ProbabilityA sporting goods store specializes in mountain bikes. Each week, two dozen mountain bikes are randomly selected from the store's warehouse
to undergo a performance test.
What is the population for the performance test?
A.The population is all of the mountain bikes in the store's warehouse.
B.The population is all of the merchandise sold by the store.
C. The population is the mountain bikes that are not randomly selected.
D. The population is the salespersons at the store.

Math
ProbabilityA committee has nine members. There are three members that currently serve as the board's chairman, ranking member, and treasurer. Each member is equally likely to serve in any of the positions. Three members are randomly selected and assigned to be the new chairman, ranking member, and treasurer. What is the probability of randomly selecting the three members who currently hold the positions of chairman, ranking member, and treasurer and reassigning them to their current positions? The probability is

Math
ProbabilityA basketball player routinely hits 100% of their free throws. What is the probability this player at practice only makes 2 out of 11 free throws? Express your answer as a percent rounded to the nearest tenth.
0.0%
0.5%
1.4%
2.9%
Math
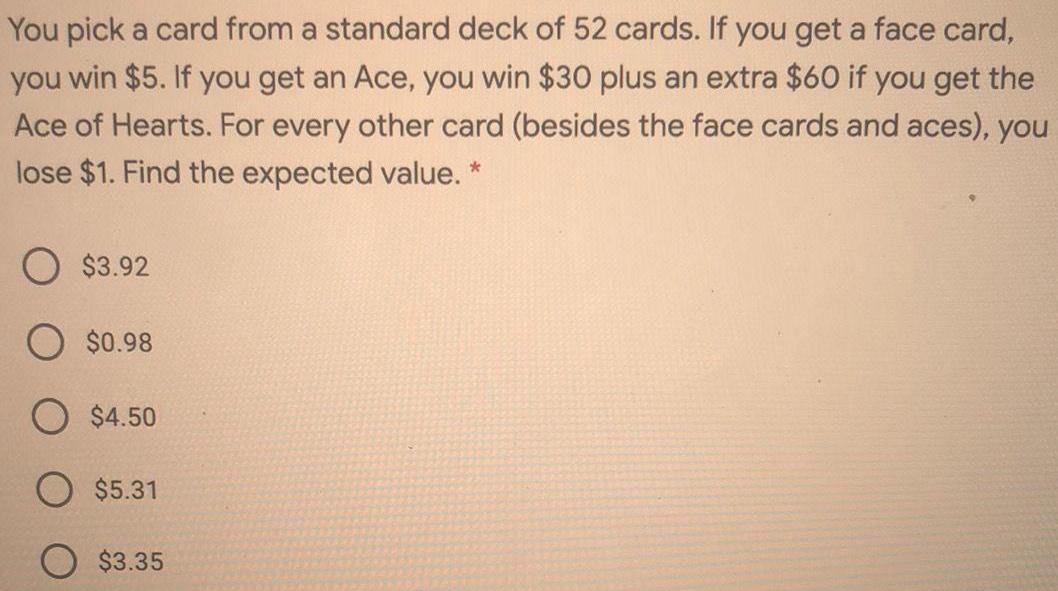
ProbabilityYou pick a card from a standard deck of 52 cards. If you get a face card, you win $5. If you get an Ace, you win $30 plus an extra $60 if you get the Ace of Hearts. For every other card (besides the face cards and aces), you lose $1. Find the expected value. *
$3.92
$0.98
$4.50
$5.31
$3.35

Math
Probability37% of U.S. adults say they are more likely to make purchases during a sales tax holiday. You randomly select 10 adults. Find the probability that the number of adults who say they are more likely to make purchases during a sales tax holiday is (a) exactly two, (b) more than two, and (c) between two and five, inclusive.
(a) P(2)= 0.153 (Round to the nearest thousandth as needed.)
(b) P(x > 2) = 0.779 (Round to the nearest thousandth as needed.)
(c) P(2 ≤x≤5)=(Round to the nearest thousandth as needed.)

Math
ProbabilityA coin of questionable fairness is tossed 10 times per set of trials for two sets of trials. The outcomes are THTHTHTHHT and TTTHTTHTTH (T= Tails; H = Heads). Which model can you most likely rule out on the basis of this simulation?
A. The probability of heads is 40%.
B. The probability of heads is 30%.
C.The probability of heads is 35%.
D. The probability of heads is 70%.

Math
ProbabilityThere are seven white dogs, five black dogs, six white cats, and three black cats. What is the probability of randomly selecting a white animal or a dog?

Math
Probability53% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults. Find the probability that the number of U.S. adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four.
(a) P(5)=
(Round to three decimal places as needed.)
(b) P(x ≥ 6) =
(Round to three decimal places as needed.)
(c) P(x<4)=
(Round to three decimal places as needed.)

Math
Probability56% of U.S. adults have very little confidence in newspapers. You randomly select 10 U.S. adults. Find the probability that the number of U.S. adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four.

Math
ProbabilityIn a recent survey, 73% of the community favored building a police substation in their neighborhood. If 14 citizens are chosen, find the probability that exactly 8 of them favor the building of the police substation.
0.094
0.571
0.730
0.013

Math
ProbabilityDetermine which numbers could not be used to represent the probability of an event.
Select all that apply.
A. 320/1058 because probability values cannot be in fraction form.
B. 33.3%, this is because probability values cannot be greater than 1.
C. 64/25, because probability values cannot be greater than 1.
D. 0, because probability values must be greater than 0.
E. 0.0002, because probability values must be rounded to two decimal places.
F. -1.5, because probability values cannot be less than 0.

Math
Probability17% adults favor the use of unmanned drones by police agencies. Twelve U.S. adults are randomly selected. Find the probability that the number of U.S. adults who favor the use of unmanned drones by police agencies is (a) exactly three, (b) at least four, (c) less than eight.

Math
ProbabilityThere are 3 apples, 4 oranges, and a pear in a basket. Determine each probability that you select an orange and then a pear at random without replacement. Write your answer as a fraction. 2 out of 5 would be typed as 2/5.

Math
ProbabilityA shipment of 12 microwave ovens contains 2 defective units. A restaurant buys four of these units. What is the probability of the restaurant buying at least three nondefective units?
The probability of the restaurant buying at least three nondefective units is
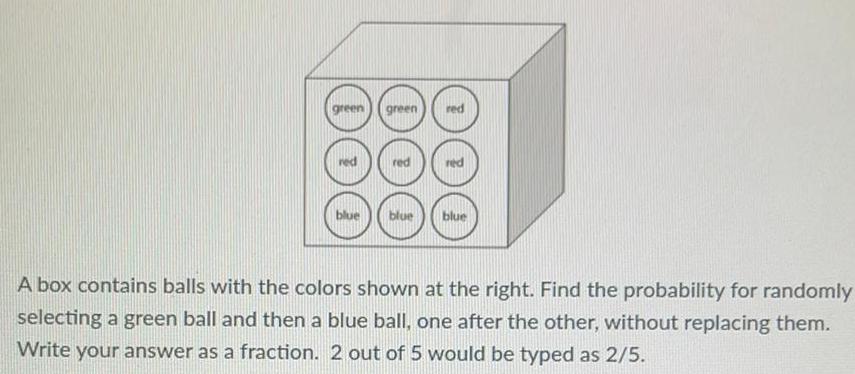
Math
Probabilitygreen green red
red red red
blue blue blue
A box contains balls with the colors shown at the right. Find the probability for randomly
selecting a green ball and then a blue ball, one after the other, without replacing them.
Write your answer as a fraction. 2 out of 5 would be typed as 2/5.

Math
ProbabilityDetermine whether the distribution is a discrete probability distribution.
Is the distribution a discrete probability distribution? Why? Choose the correct answer below.
A. No, because some of the probabilities have values greater than 1 or less than 0.
B. Yes, because the probabilities sum to 1 and are all between 0 and 1, inclusive.
C. No, because the total probability is not equal to 1.
D. Yes, because the distribution is symmetric.

Math
ProbabilityAn analog stopwatch has 60 tick marks, one for each second. After the stopwatch has been running for a few minutes, it is stopped randomly. What is the probability of the stopwatch's hand landing on the 9, 30, 45, or 51?
9.1%
7.9%
7.3%
6.7%

Math
ProbabilityA warehouse employs 21 workers on first shift, 15 workers on second shift, and 10 workers on third shift. Eight workers are chosen at random to be interviewed about the work environment. Find the probability of choosing exactly five first-shift workers.
The probability of choosing exactly five first-shift workers is

Math
ProbabilityA probability experiment consists of rolling a 6-sided die. Find the probability of the event below. rolling a number less than 3
The probability is

Math
ProbabilityA local ice cream store sells three flavors of ice cream during a busy summer month. During this month, there were 566 orders of vanilla ice cream, 400 orders of strawberry ice cream, and 1,224 orders of chocolate ice cream. What is the experimental probability that chocolate ice cream was ordered during this month?

Math
ProbabilityYou randomly select an integer from 0 to 7 (inclusively) and then randomly select an integer from 0 to 4 (inclusively). What is the probability of selecting a 3 both times?
The probability is

Math
ProbabilitySuppose the weights of all DVC students are normally distributed with mean 168.2 pounds and standard deviation 22.1 pounds.
(a) If one student is randomly selected, find the probability that the student weighs more than 180 pounds.
(b) The elevator in the Math Building can safely lift 1,800 pounds; it is dangerous if the total weight is over 1,800 pounds. If 10 people are in the elevator, find the probability that their mean weight is greater than 180 pounds (hence, the total weight exceeds 1,800 pounds). Is it safe to have 10 people in the elevator? Explain.

Math
ProbabilityDetermine whether the events are independent or dependent. Explain your reasoning.
Returning a rented movie after the due date and receiving a late fee

Math
Probability32% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit cards. Find the probability that the number of college students who say they use credit cards because of the rewards program is (a) exactly two, (b) more than two, and (c) between two and five inclusive. If convenient, use technology to find the probabilities. )

Math
ProbabilityA 12-sided die is rolled. The set of equally likely outcomes is {1,2,3,4,5,6,7,8,9,10,11,12). Find the probability of rolling a number greater than 2.
The probability of rolling a number greater than 2 is
(Type an integer or a simplified fraction.)
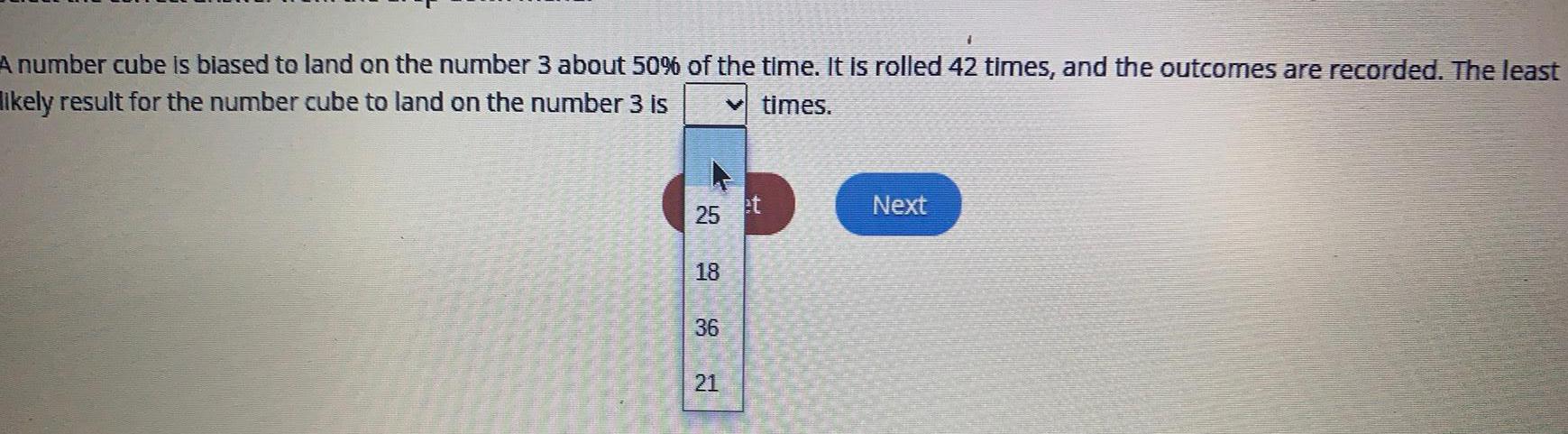
Math
ProbabilityA number cube is biased to land on the number 3 about 50% of the time. It is rolled 42 times, and the outcomes are recorded. The least likely result for the number cube to land on the number 3 is times.
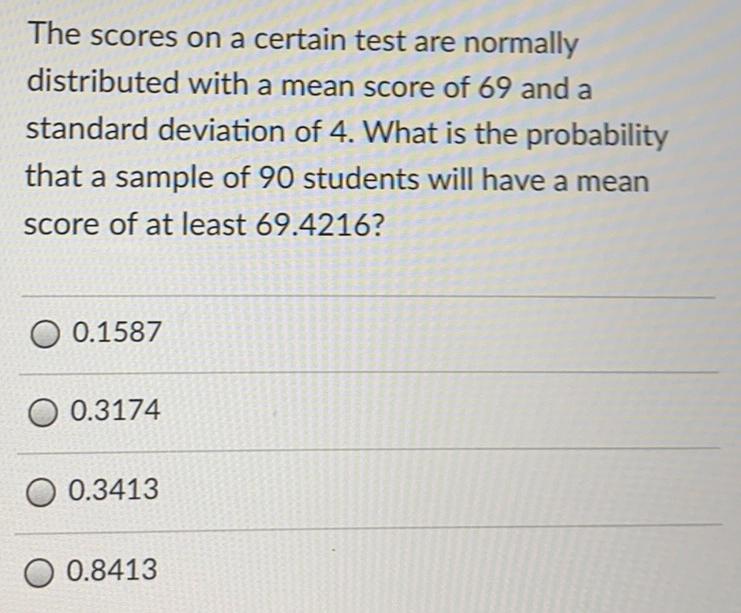
Math
ProbabilityThe scores on a certain test are normally distributed with a mean score of 69 and a standard deviation of 4. What is the probability that a sample of 90 students will have a mean score of at least 69.4216?
0.1587
0.3174
0.3413
0.8413

Math
ProbabilityIt has been reported that 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice. Suppose Chevrolet did a study of a random sample of 1006 Chevrolet owners and found that 490 said that they would buy another Chevrolet. Does this indicate that the population proportion of consumers loyal to Chevrolet is more than 47%? Use a = 0.01.

Math
ProbabilityA math class has 7 girls and 1 boy in the seventh grade and 2 girls and 6 boys in the eighth grade. The teacher randomly selects a seventh grader and an eighth grader from the class for a competition. What is the probability that the students she selects are both boys? Write your answer as a fraction in simplest form.

Math
ProbabilityThe probability that a tennis set will go to a tiebreaker is 16%. In 420 randomly selected tennis sets, what is the mean and the standard deviation of the number of tiebreakers?
mean: 67.2; standard deviation: 8.2
mean: 63; standard deviation: 7.51
mean: 67.2; standard deviation: 7.51
mean: 63; standard deviation: 8.2

Math
ProbabilityA doctor gives a patient a 60% chance of surviving bypass surgery after a heart attack. If the patient survives the surgery, then the patient has a 25% chance that the heart damage will heal. Find the probability that the patient survives the surgery and the heart damage heals.
The probability is
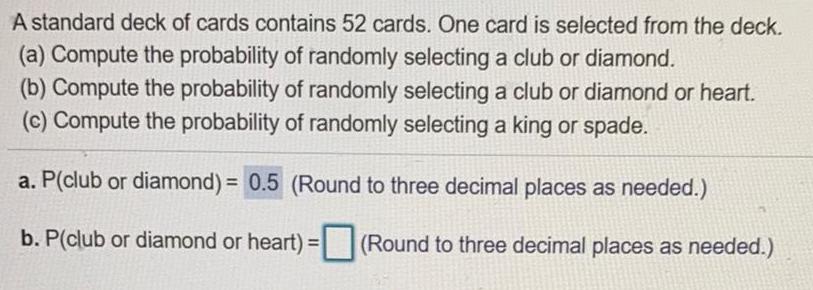
Math
ProbabilityA standard deck of cards contains 52 cards. One card is selected from the deck.
(a) Compute the probability of randomly selecting a club or diamond.
(b) Compute the probability of randomly selecting a club or diamond or heart.
(c) Compute the probability of randomly selecting a king or spade.
a. P(club or diamond) = 0.5 (Round to three decimal places as needed.)
b. P(club or diamond or heart) = (Round to three decimal places as needed.)

Math
ProbabilityA small corporation must appoint four officers (a president, a chief executive officer, a chief operating
officer, and a chief financial officer). It must also appoint a Strategic Planning Committee with four people on
it. There are a total of 9 qualified candidates, and the chosen officers may also serve on the committee.
(a) How many different ways can the four officers be appointed?
(b) How many different ways can the committee of four be appointed?
(c) What is the probability of randomly selecting the committee members and getting the four youngest of the
qualified candidates?

Math
ProbabilityYou randomly select an integer from 0 to 24 (inclusively) and then randomly select an integer from 0 to 39 (inclusively). What is the probability of selecting an 18 both times?

Math
ProbabilityTwo number cubes are rolled for two separate events:
Event A is the event that the sum of numbers on both cubes is less than 10.
Event B is the event that the sum of numbers on both cubes is a multiple of 3.
In terms of a reduced fraction, find the conditional probability of B given that A occurs first.

Math
ProbabilitySuppose that the probabilities of a customer purchasing 0, 1, or 2 books at a book store are 0.3, 0.2, and 0.5, respectively. What is the expected number of books a customer will purchase
The expected number of books that the customer will purchase is
(Type an integer or a decimal.)

Math
Probability39.9% of consumers believe that cash will be obsolete in the next 20 years. Assume that 6 consumers are randomly selected Find the probability that fewer than 3 of the selected consumers believe that cash will be obsolete in the next 20 years.
The probability is
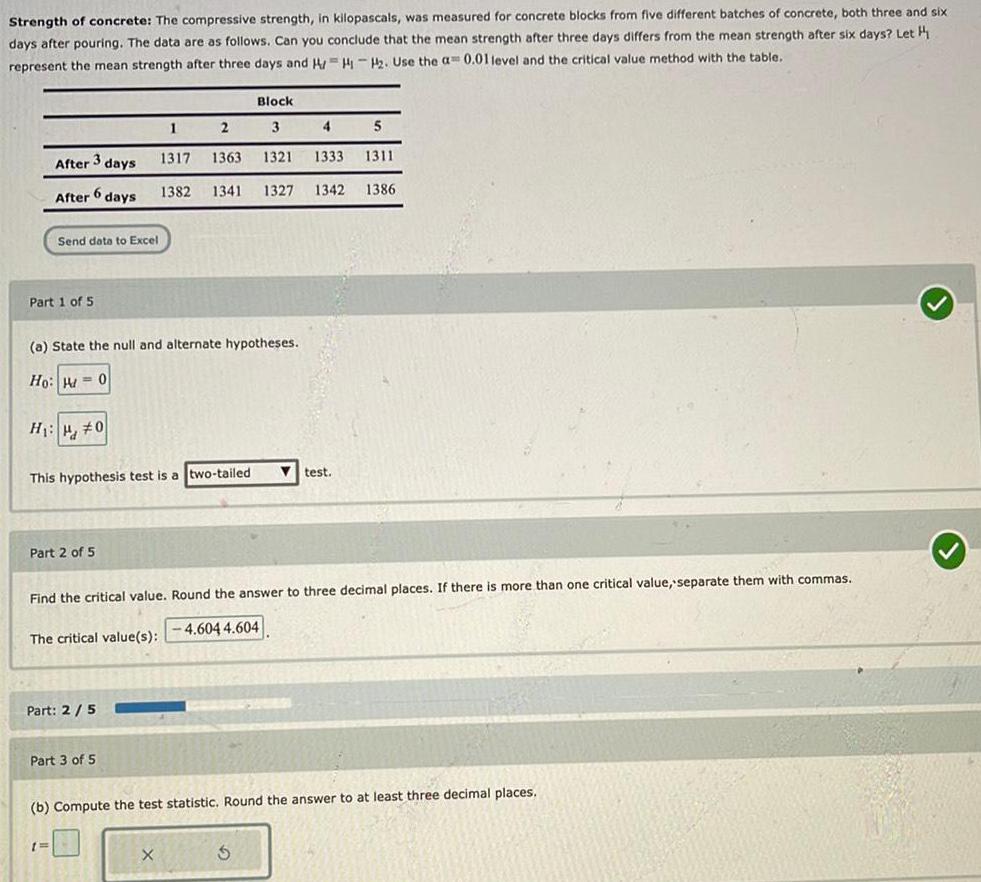
Math
ProbabilityStrength of concrete: The compressive strength, in kilopascals, was measured for concrete blocks from five different batches of concrete, both three and six days after pouring. The data are as follows. Can you conclude that the mean strength after three days differs from the mean strength after six days? Let H represent the mean strength after three days and HH₁-H₂. Use the a 0.01 level and the critical value method with the table.
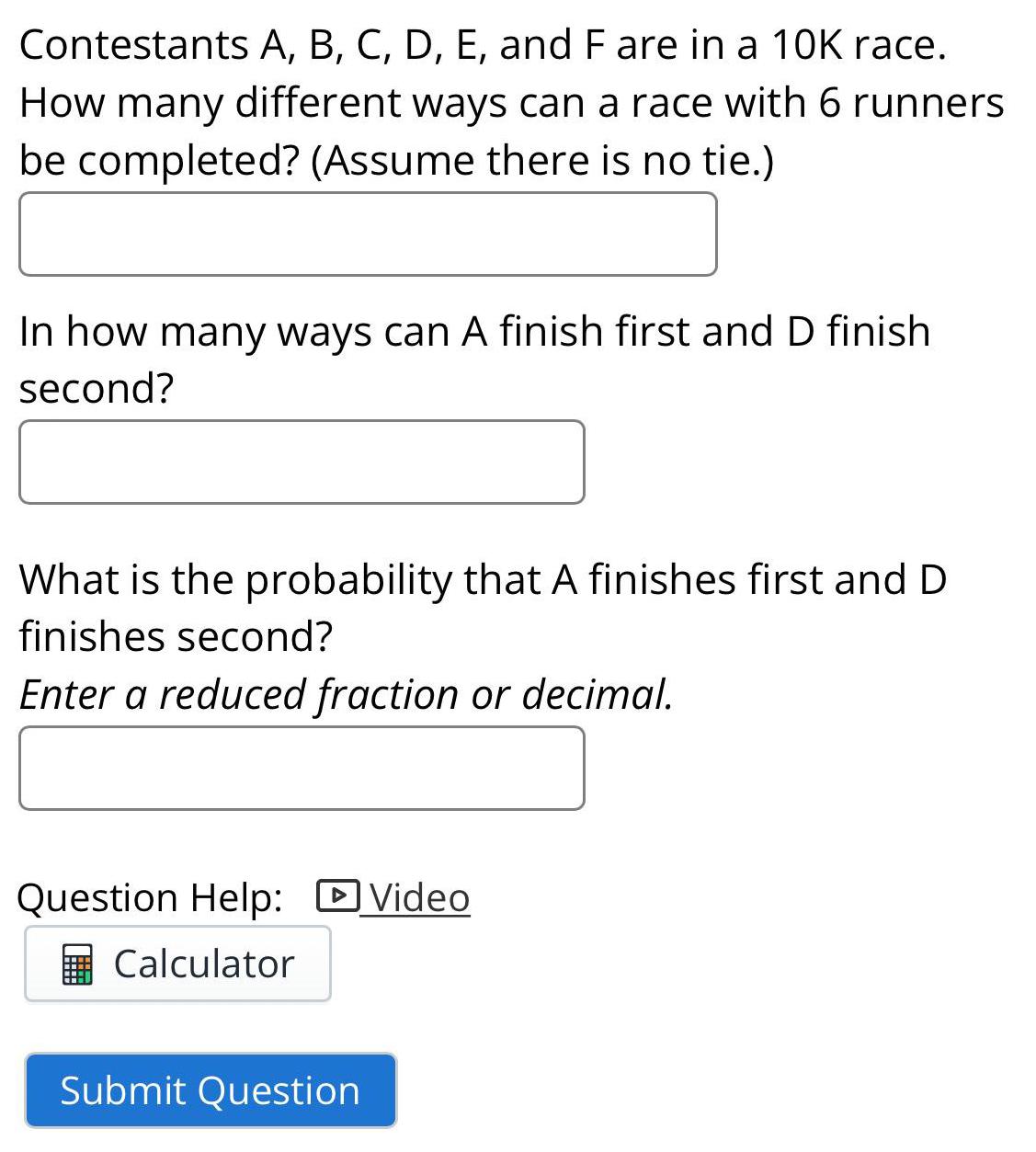
Math
ProbabilityContestants A, B, C, D, E, and F are in a 10K race. How many different ways can a race with 6 runners be completed? (Assume there is no tie.)
In how many ways can A finish first and D finish second?
What is the probability that A finishes first and D finishes second?
Enter a reduced fraction or decimal.

Math
ProbabilityGiven event T1, T2, T3, and D with p(D)=0.05, p(T1|D)=p(~T1|~D)=0.9, p(T2|D)=p(~T2|~D)=0.8, p(T3|D)=0.9 and p(~T3|~D)=1, find p(T1u T2uT3) if p(T∩T2)=0.05, p(T∩T3)=0.01, and T2 and T3 are mutually exclusive.
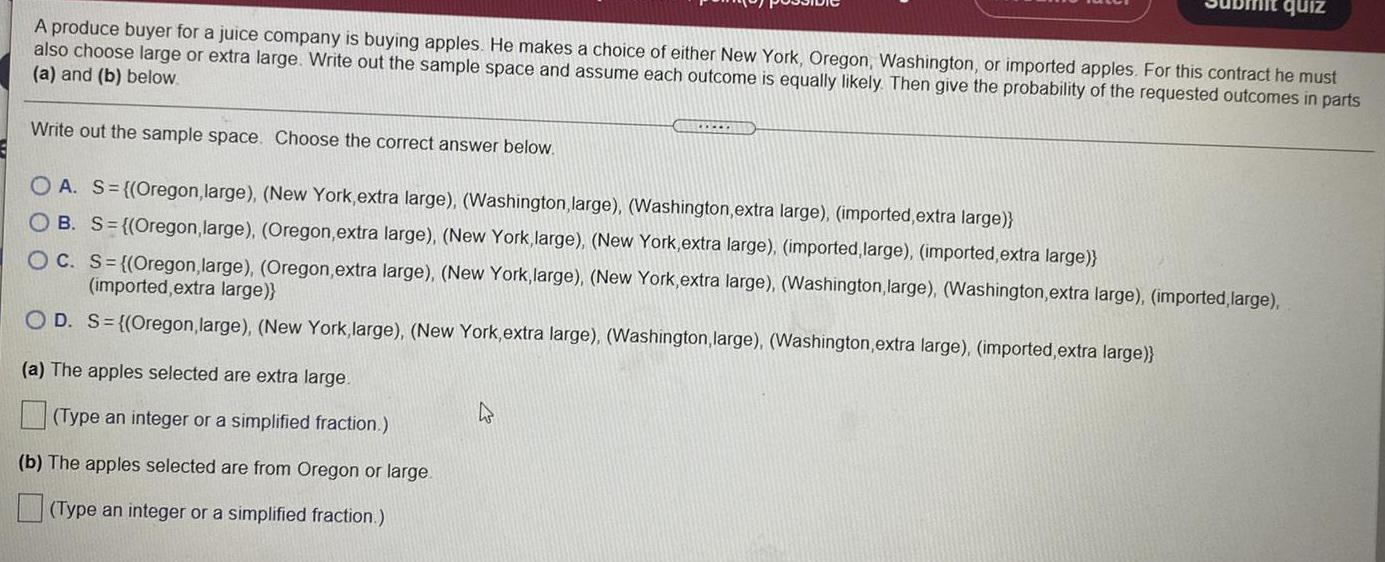
Math
ProbabilityA produce buyer for a juice company is buying apples. He makes a choice of either New York, Oregon, Washington, or imported apples. For this contract he must
also choose large or extra large. Write out the sample space and assume each outcome is equally likely. Then give the probability of the requested outcomes in parts
(a) and (b) below.
Write out the sample space. Choose the correct answer below.
A. S=((Oregon, large), (New York,extra large), (Washington, large), (Washington, extra large), (imported, extra large)}
B. S={(Oregon, large), (Oregon, extra large), (New York, large), (New York,extra large), (imported, large), (imported, extra large)}
C. S={(Oregon, large), (Oregon, extra large), (New York, large), (New York, extra large), (Washington, large), (Washington, extra large), (imported, large),
(imported,extra large)}
D. S={(Oregon, large), (New York,large), (New York,extra large), (Washington, large), (Washington,extra large), (imported,extra large)}
(a) The apples selected are extra large.
(Type an integer or a simplified fraction.)
(b) The apples selected are from Oregon or large.
(Type an integer or a simplified fraction.)

Math
ProbabilityA media rental store rented the following number of movie titles in each of these categories: 178 horror, 248 drama, 118 mystery, 326 romance, and 134 comedy. If a person selects a movie to rent, find the probability that it is a horror or comedy.

Math
ProbabilityTiles containing the letters for the word "ENCYCLOPEDIA" are placed in a bag. If you reach into the bag and select one tile at random, what are the odds against drawing the letter E?
Math
ProbabilityA marble is drawn from a box containing 3 yellow, 5 white, and 13 blue marbles. Find the odds in favor of drawing the following
(a) A yellow marble
(b) A blue marble
(c) A white marble
(a) In reduced form, the odds in favor of drawing a yellow marble are
(Simplify your answers.)
(b) In reduced form, the odds in favor of drawing a blue marble are
(Simplify your answers.)
(c) In reduced form, the odds in favor of drawing a white marble are
(Simplify your answers.)

Math
ProbabilityYou toss a fair coin 5 times. What is the probability of at least one head? Round to the nearest ten-thousandth.
0.0313
0.5000
0.9688
0.7500