Probability Questions and Answers

Math
ProbabilityYou are earning a salary of $80,000 a year, and your position is steady. However, you have an opportunity to start your own business. You have done the research and It has shown that starting your own company gives you a 20% chance of earning $400,000 a year, a 30% chance of earning $100,000 a year, and a 50% chance of complete fallure. What is the expected value of giving up your $80,000 salary and starting your own business?
$45,000
$12,000
-$4,600
$30,000

Math
ProbabilitySuppose the probability an Insurance salesman makes a sale (the probability of success) is 0.6. Would you use a binomial distribution or geometric distribution to determine the probability that the salesman makes the first sale on the third presentation? What Is that probability?
binomial; 0.096
geometric; 0.096
binomial; 0.144
geometric: 0.144
Math
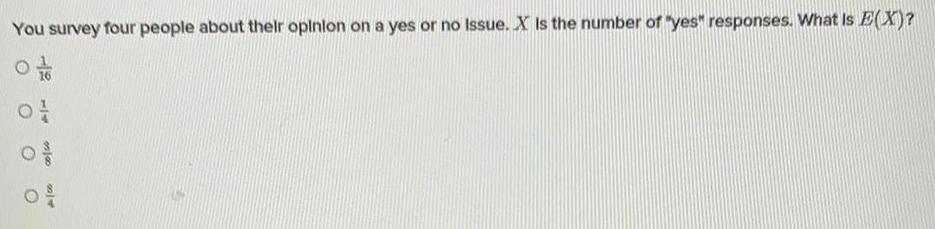
ProbabilityYou survey four people about their opinion on a yes or no Issue. X Is the number of "yes" responses. What is E(X)?
1/16
1/4
3/8
8/4
Math
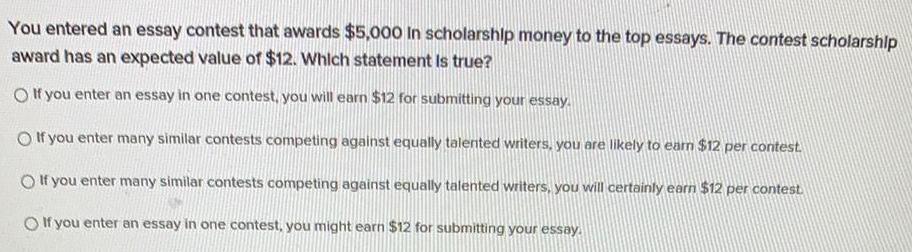
ProbabilityYou entered an essay contest that awards $5,000 In scholarship money to the top essays. The contest scholarship award has an expected value of $12. Which statement is true?
If you enter an essay in one contest, you will earn $12 for submitting your essay.
If you enter many similar contests competing against equally talented writers, you are likely to earn $12 per contest.
If you enter many similar contests competing against equally talented writers, you will certainly earn $12 per contest.
If you enter an essay in one contest, you might earn $12 for submitting your essay.
Math
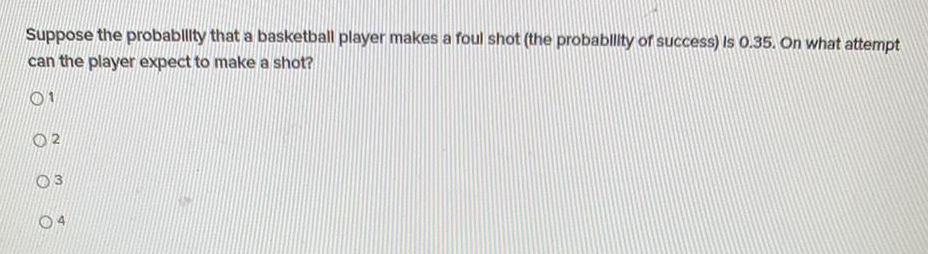
ProbabilitySuppose the probability that a basketball player makes a foul shot (the probability of success) is 0.35. On what attempt can the player expect to make a shot?
1
2
3
4

Math
ProbabilityCaptive primates, such as monkeys, often experience fractured bones. The probability distribution from a study of the X- rays of 500 captive spider monkeys shows that fifteen percent of them had one healed fracture; twenty percent had two healed fractures; twenty-five percent had three healed fractures; and forty percent had four healed fractures. About how many healed fractures would you expect a randomly selected captive spider monkey to have based on this probability distribution?

Math
ProbabilityYou ask four people to the prom. If X is the number of "yes" responses, what is E(X)? Assume equal probability for "yes" and "no" response.

Math
ProbabilityWhich statements about a probability distribution are always true?
The probability of an outcome is never 0.
The expected value of a probability distribution is the mean of the distribution.
The sum of the probabilities in a probability distribution is equal to 1.
Values for for a discrete random variable X in a probability distribution are always positive.
A probability distribution must have more than one outcome.
Math
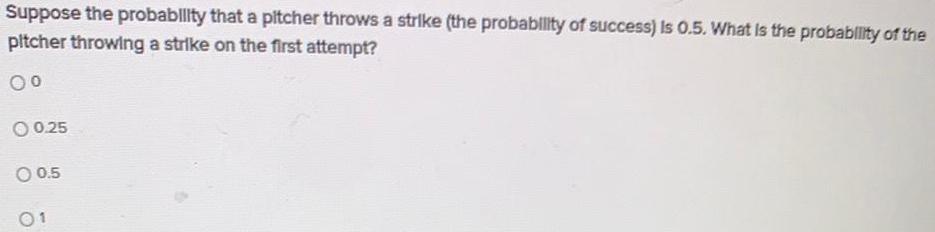
ProbabilitySuppose the probability that a pitcher throws a strike (the probability of success) is 0.5. What is the probability of the pitcher throwing a strike on the first attempt?
0
0.25
0.5
1
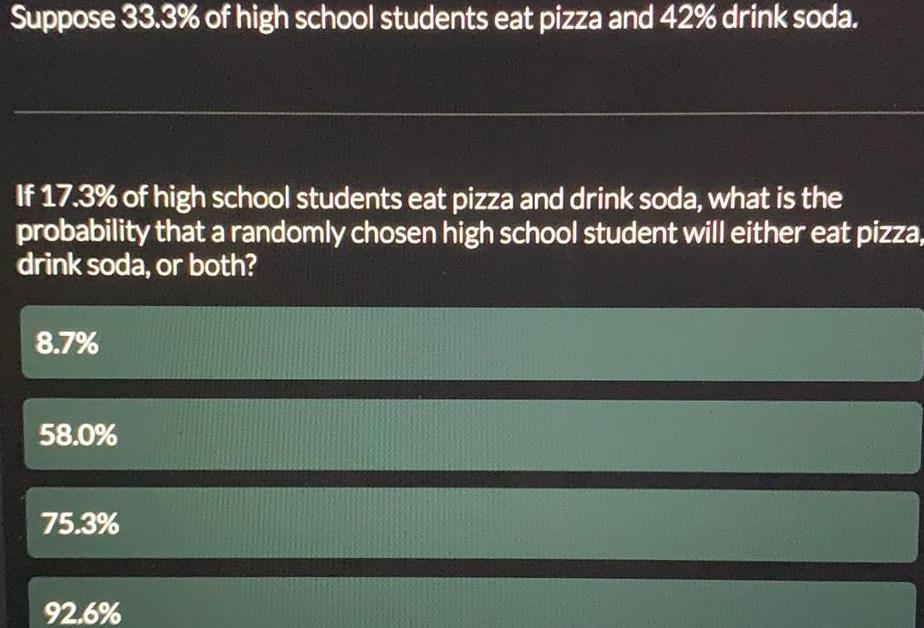
Math
ProbabilitySuppose 33.3% of high school students eat pizza and 42% drink soda. If 17.3% of high school students eat pizza and drink soda, what is the probability that a randomly chosen high school student will either eat pizza, drink soda, or both?
8.7%
58.0%
75.3%
92.6%

Math
ProbabilityWhich of the following is NOT a characteristic of the chi-square distribution?
The chi-square curve approaches, but never touches, the positive horizontal axis.
The mean of the chi-square distribution is located to the left of the peak.
The chi-square curve is nonsymmetrical.
As the degrees of freedom increases, the chi-square curves look more and more like a normal curve.

Math
ProbabilityThere are twelve songs on your playlist. Six of them are country and six are pop. With random shuffle and no repetition, you listen to six songs. What is the probability that you listened to all country songs?

Math
ProbabilityHow can you use a simulation with a number cube to collect data for an event that has two possible outcomes that each have a probability of 0.5? Select all that apply.
Let the odd numbers represent one outcome and the even numbers represent the other outcome.
Let numbers 1-3 represent one outcome and numbers 4-6 represent the other outcome.
Let number 1 represent one outcome and number 6 represent the other outcome.
Let numbers 1 and 2 represent one outcome and numbers 3-6 represent the other outcome.
Let numbers 1-4 represent one outcome and numbers 5 and 6 represent the other outcome.

Math
ProbabilityA tile is drawn at random from the tiles below. What is the probability that it is a consonant and has a point-value that is less than 3? Write your answer as a fraction in simplest form.

Math
ProbabilityA brand of jeans comes in nine different washes, five different fit styles, and three different height options. If two of the wash options are out of stock, how many ways can someone order a single pair of jeans?
A. 95
B. 105
C. 120
D. 15

Math
ProbabilityCaptive primates, such as spider monkeys, often experience fractured bones. The probability distribution from a study of
the X-rays of 500 captive spider monkeys shows that half of them had one healed fracture; one-quarter had two healed
fractures; ten percent had three healed fractures; and fifteen percent had four healed fractures. About how many healed
fractures would you expect a randomly selected captive spider monkey to have based on this probability distribution?
01
02
03
04


Math
ProbabilityIf the expected value for a probability distribution from a study of penguin births recorded In U.S. zoos in 2018 equals 2.4578, what does this value tell you?
expect that any randomly selected U.S. zoo had between 24 and 25 penguin births in 2018
expect that all U.S. zoos had 2.4578 penguins born in 2018
expect that about 2.5% of U.S. zoos had a penguin birth in 2018
expect any randomly selected U.S. zoo recorded between 2 and 3 penguin births in 2018
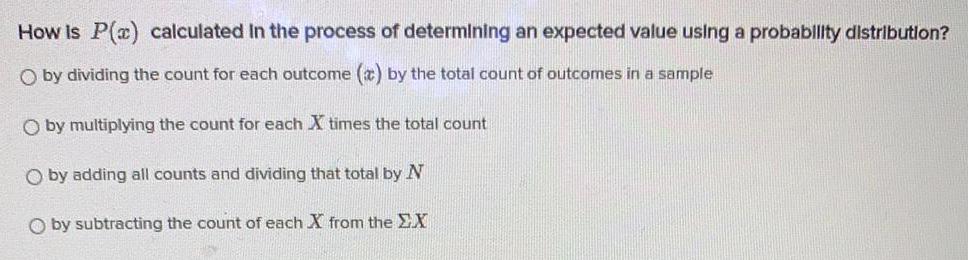
Math
ProbabilityHow is P(x) calculated in the process of determining an expected value using a probability distribution?
by dividing the count for each outcome (x) by the total count of outcomes in a sample
by multiplying the count for each X times the total count
by adding all counts and dividing that total by N
by subtracting the count of each X from the EX

Math
ProbabilityWhat is the total probability of getting one of the two following outcomes with three number generators, assuming the number generators are binary?
(0, 1, 0) and (1, 0, 1)
1/4
1/8
3/4
3/4

Math
Probability8. A card is chosen at random from a standard deck. Find each probability as a fraction (in simplest form). decimal, and percent.
a) P(ace)
c) P(face card or 8)
b) P(black or queen)
d) P(red jack)

Math
ProbabilityThere are 15 candidates for three positions at a restaraunt. One position is for a cook. The second position is for a food server. The third position is for a cashier. If all 15 candidates are equally qualified for the three positions, in how many different ways can the three positions be filled?

Math
ProbabilityGeneva has learned that the expected value of an Insurance payment to a driver to cover the costs of an accident in her state Is $5,200 over the first three years. If her Insurance costs $2,000 a year and the average cost of an accident Is $1,000, which statement is most correct?
If Geneva drives more recklessly than most other drivers, the insurance is a good decision for Geneva.
If Geneva drives more carefully than most other drivers, the insurance is a good decision for Geneva.
Geneva knows she will certainly come out ahead and make money by paying for the insurance.
Geneva knows she will certainly lose money by paying for the insurance.

Math
ProbabilityThree hundred students submitted an essay In a nationwide essay contest. The best essay will win a $2,000 scholarship. Ten other students will be given a $1,000 scholarship. What is the expected value of an essay submission?
$40
$0.04
$12,000
$1,500

Math
ProbabilitySuppose the probability of a pitcher throwing a strike (the probability of success) is 0.5. After how any pitches is a strike expected?
1
2
3
5
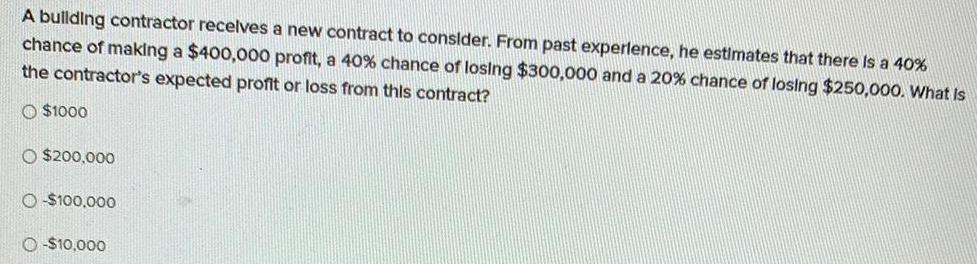
Math
ProbabilityA building contractor receives a new contract to consider. From past experience, he estimates that there is a 40% chance of making a $400,000 profit, a 40% chance of losing $300,000 and a 20% chance of losing $250,000. What Is the contractor's expected profit or loss from this contract?
$1000
$200,000
-$100,000
-$10,000
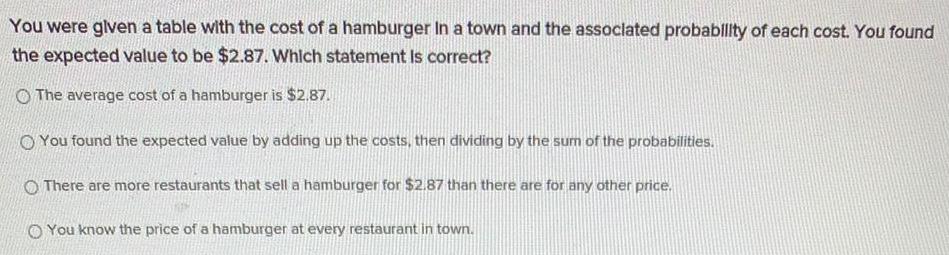
Math
ProbabilityYou were given a table with the cost of a hamburger In a town and the associated probability of each cost. You found
the expected value to be $2.87. Which statement is correct?
The average cost of a hamburger is $2.87.
You found the expected value by adding up the costs, then dividing by the sum of the probabilities.
There are more restaurants that sell a hamburger for $2.87 than there are for any other price.
You know the price of a hamburger at every restaurant in town.

Math
ProbabilityWhich of the following correctly describes expected value?
the long-term mean of all possible outcomes in a probability distribution
the probability distribution of the means of all outcome variables
the set of all outcomes in a discrete variable set
the first value in a variable set greater than one

Math
ProbabilityIn a certain city in Washington, the grass grows at the rate of 1/2 Inch a day on sunny days. On cloudy days, the grass grows at the rate of 1/4 Inch per day. In a typical July, 75% of the days are sunny and 25% are cloudy. Determine the total number of Inches of expected growth In a typical July.
0.43 inches
12.5 inches
15.5 inches
2.34 inches

Math
ProbabilityHow can you use a simulation to collect data for an event that has two possible outcomes that each have a probability of 0.5?
Use a coin and let heads represent one outcome and tails represent the other outcome.
Use a random number generator and let each number represent the different outcomes.
Use a deck of playing cards and let number cards represent one outcome and let face cards represent the other outcome.
Use a spinner with four sections and let one section represent one outcome and three sections represent the other outcome.

Math
ProbabilityHector plays a game with a friend. They pay $1 and roll a 6-sided die. If the die comes up a number that is larger than 2, they win $7. If it doesn't, they win nothing. What is the expected value of the game? Give your answer to the closest cent (two decimal places).

Math
ProbabilityA study determined that 9% of children under 18 years of age live with their father only. Find the probability that at most 2 persons selected at random from 10 children under 18 years of age lived with their father only.

Math
ProbabilityGiven P(A) = 0.36, P(B) = 0.2 and P(An B) = 0.122, find the value of P(AUB), rounding to the nearest thousandth, if necessary.

Math
ProbabilityA student of elite distance runners found a mean body weight of 63.1 kg, with a standard deviaiton of 4.8 kg. What proportion of runners have body weights below 60 kg? Round your answer to the nearest integer.

Math
ProbabilityA laundry detergent company's 32-ounce bottles pass inspection 98/100 of the time. If the bottle does not pass inspection, the company loses the unit cost for each bottle of laundry detergent that does not pass inspection, which is $3.45. If 800 bottles of laundry detergent are produced, about how much money can the company expect to lose?

Math
Probabilityhere are two Statistics class in the high school. Andrea is in the AP class with 12 students and Drew is in the regular class with 18 students. If one student from each class will be chosen, what is the probability that both Andrea and Drew will be chosen.

Math
ProbabilityA study determined that 5% of children under 18 years old lived with their father only. Find the probability that none of the children selected at random from 15 children under 18 years old lived with their father only.

Math
Probability11.9% of the population is 65 or older. Find the probability that the following number of persons selected at random from 25 people are 65 or older.
The probability that at least 3 are 65 or older is
(Round to three decimal places as needed.)

Math
ProbabilityIn a class of 28 students, 10 are female and 15 have an A in the class. There are 4 students who are female and have an A in the class. What is the probability that a student chosen randomly from the class is a female who has an A?
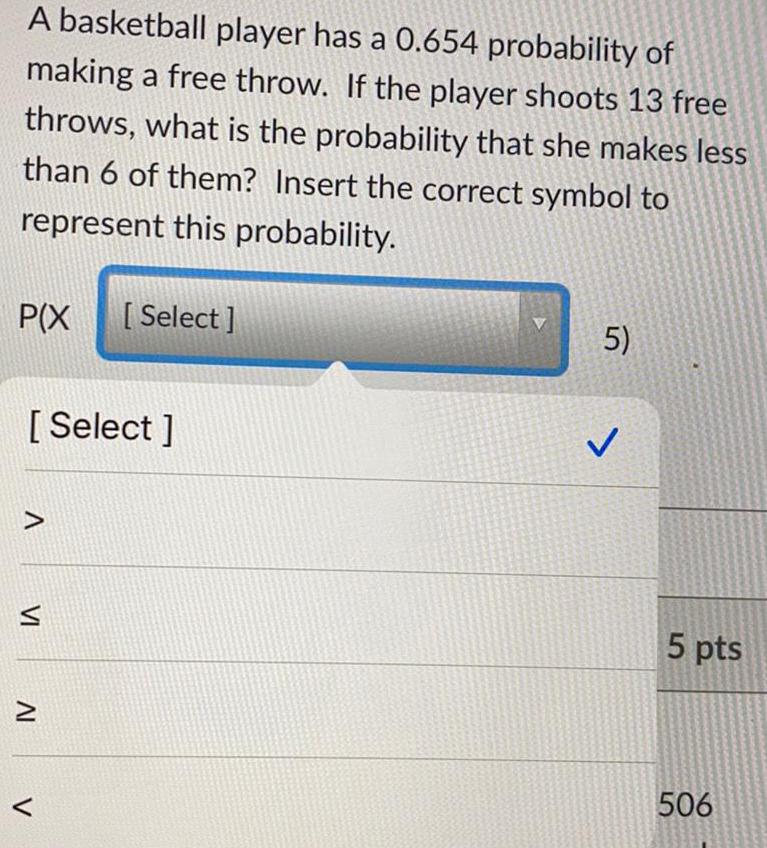
Math
ProbabilityA basketball player has a 0.654 probability of making a free throw. If the player shoots 13 free throws, what is the probability that she makes less than 6 of them? Insert the correct symbol to represent this probability.

Math
ProbabilityThe city council conducts a survey of the city's residents to determine which services are most used by the community. 60% of the residents say that they use the library, and 35% of the residents say they use the library and the recycling center.
What is the probability that a resident uses the recycling center given that they use the library? Express your answer as a decimal rounded to three decimal places.
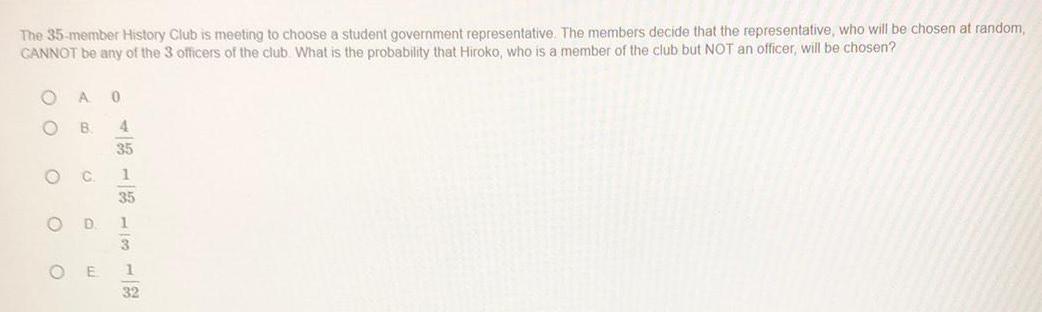
Math
ProbabilityThe 35-member History Club is meeting to choose a student government representative. The members decide that the representative, who will be chosen at random, CANNOT be any of the 3 officers of the club. What is the probability that Hiroko, who is a member of the club but NOT an officer, will be chosen?

Math
ProbabilityA bag contains 5 blue marbles, 4 red marbles, and 3 orange marbles. Mrs. Cox picks one without looking, replaces it and picks another one. What is the probability that she picks two that are not orange?
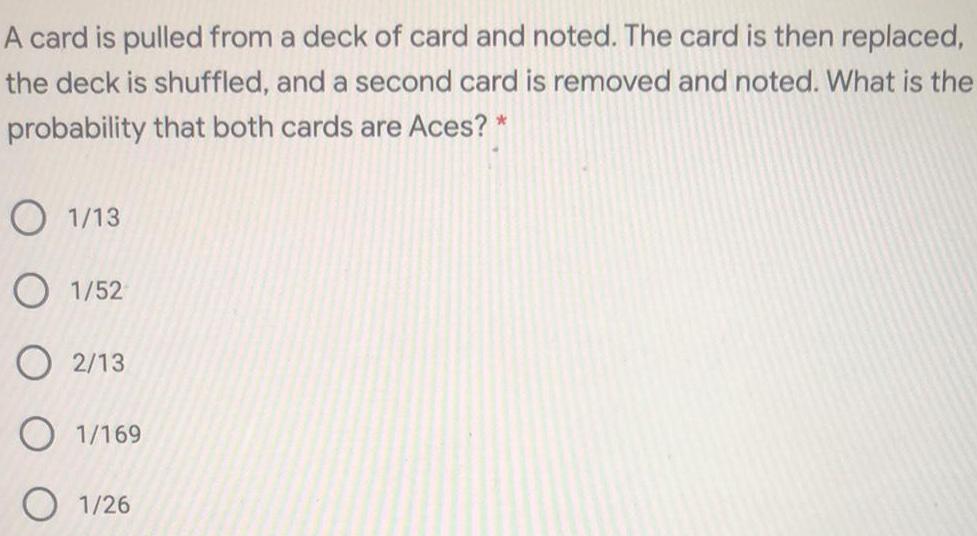
Math
ProbabilityA card is pulled from a deck of card and noted. The card is then replaced,
the deck is shuffled, and a second card is removed and noted. What is the
probability that both cards are Aces? *
1/13
1/52
2/13
1/169
1/26

Math
ProbabilityAmong the students in a local school division, ACT scores were normally distributed this year with a mean score of 20.7 and a standard deviation of 5.9. SAT scores were normally distributed with a mean score of 1075 and a standard deviation of 168. Who scored better on their standardized test with respect to the other test takers in the school division, Jamal who took the ACT and score 29 or Shamar who took the SAT and scored 1240?
Jamal
Shamar
Both Jamal and Shamar
Neither Jamal or Shamar
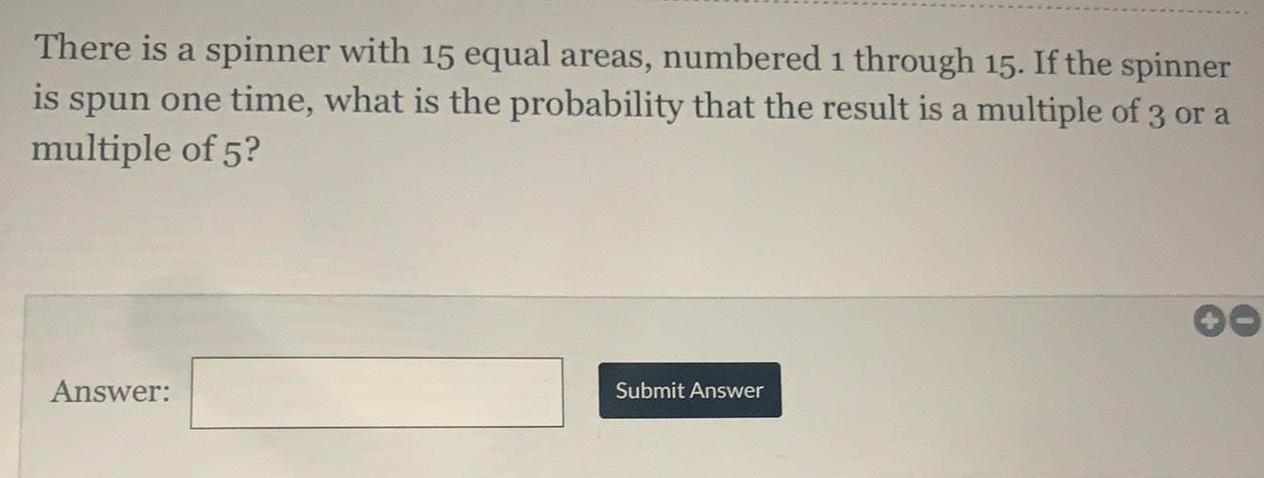
Math
ProbabilityThere is a spinner with 15 equal areas, numbered 1 through 15. If the spinner is spun one time, what is the probability that the result is a multiple of 3 or a multiple of 5?
Math
ProbabilityIn a certain Algebra 2 class of 26 students, 21 of them play basketball and 7 of them play baseball. There are 2 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?

Math
ProbabilityPeter Elzinga is a Dutch competitive archer who was ranked number 1 in
the world in 2004.
The probability that he makes a bullseye (i.e. a 10 point shot) on any given
shot is 0.95.
Assuming that the probability of making a bullseye on a given arrow is
independent of results on other arrows, what is the probability that Peter
Elzinga will make two bullseyes in a row followed by missing the bullseye on
the third shot (i.e., the probability of making a bullseye on the first and
second shots and something other than a bullseye on the third shot)?
Note: Round to the nearest thousandth if necessary.

Math
ProbabilitySuppose that a recent poll found that 64% of adults believe that the overall state of moral values is poor. Complete parts (a) through (c).
(a) For 250 randomly selected adults, compute the mean and standard deviation of the random variable X, the number of adults who believe that the overall state of moral values is poor.
The mean of X is (Round to the nearest whole number as needed.)
The standard deviation of X is. (Round to the nearest tenth as needed.)
(b) Interpret the mean. Choose the correct answer below.
A. For every 250 adults, the mean is the minimum number of them that would be expected to believe that the overall state of moral values is poor.
B. For every 250 adults, the mean is the range that would be expected to believe that the overall state of moral values is poor.
C. For every 250 adults, the mean is the number of them that would be expected to believe that the overall state of moral values is poor.
D. For every 160 adults, the mean is the maximum number of them that would be expected to believe that the overall state of moral values is poor.
(c) Would it be unusual if 148 of the 250 adults surveyed believe that the overall state of moral values is poor?
Yes
No

Math
ProbabilityA trade magazine routinely checks the drive-through service times of fast-food restaurants. A 90% confidence interval that results from examining 595 customers in one fast-food chain's drive-through has a lower bound of 159.3 seconds and an upper bound of 162.9 seconds. What does this mean?
Choose the correct answer below.
A. One can be % confident that the mean drive-through service time of this fast-food chain is seconds.
B. The mean drive-through service time of this fast-food chain is seconds % of the time.
C. There is a 90% probability that the mean drive-through service time of this fast-food chain is between seconds and seconds.
D. One can be 90% confident that the mean drive-through service time of this fast-food chain is between seconds and seconds.