Trigonometry Questions and Answers
Math
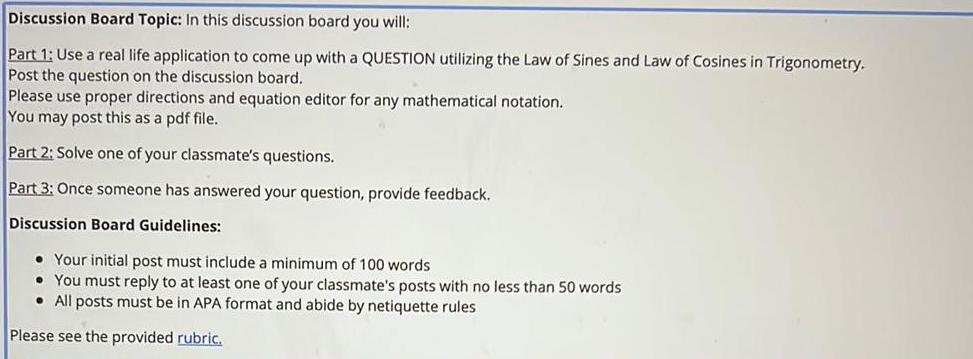
TrigonometryDiscussion Board Topic: In this discussion board you will:
Part 1: Use a real life application to come up with a QUESTION utilizing the Law of Sines and Law of Cosines in Trigonometry.
Post the question on the discussion board.
Please use proper directions and equation editor for any mathematical notation.
You may post this as a pdf file.
Part 2: Solve one of your classmate's questions.
Part 3: Once someone has answered your question, provide feedback.

Math
TrigonometryThe longer base of an isosceles trapezoid measures 23 ft. The nonparallel sides measure 9 ft, and the base angles measure 80°. Find the length of a diagonal.
A. 20 ft
B. 23 ft
C. 25 ft
D. 17 ft

Math
TrigonometryThe angle of elevation to the top of a Building in New York is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.

Math
Trigonometry4. A Ferris wheel with a diameter of 40 m rotates every 40 seconds. A passenger gets on at a point 1 m above the ground.
a) Sketch a graph showing the passenger's height during the first rotation. Be sure to label important
numbers along each axis.
b) Write an equation which expresses the height of the passenger with respect to time in seconds.
Math
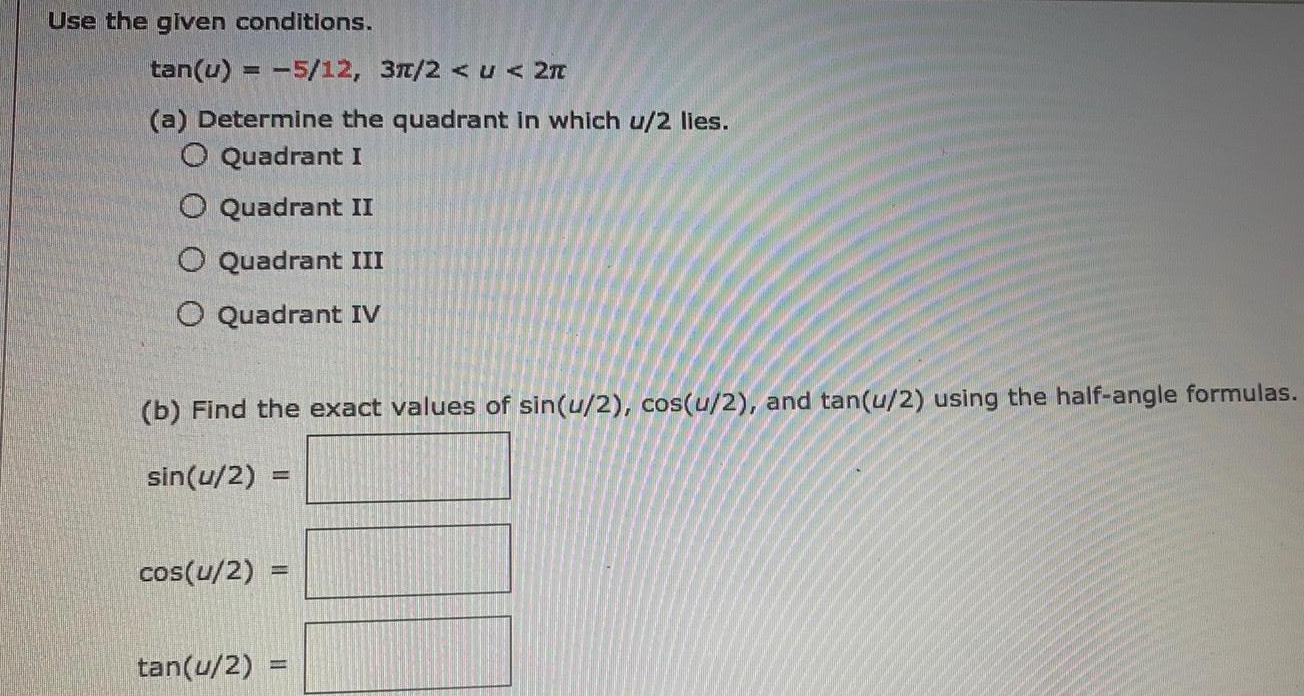
TrigonometryUse the given conditions.
tan(u) = -5/12, 3π/2 < u < 2π
(a) Determine the quadrant in which u/2 lies.
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
(b) Find the exact values of sin(u/2), cos(u/2), and tan(u/2) using the half-angle formulas.
sin(u/2) =
cos(u/2) =
tan(u/2) =
Math
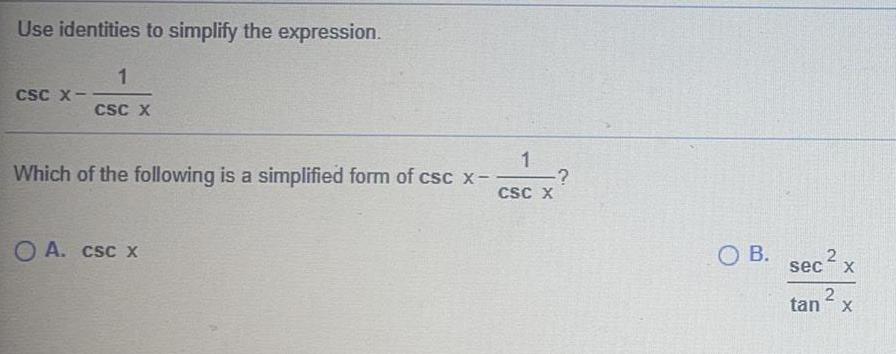
TrigonometryUse identities to simplify the expression.
CSC X-1/CSC X
Which of the following is a simplified form of csc x- 1/csc x?

Math
TrigonometryFor the given function, state the amplitude and the maximum output for the function:
f(t) = -3cos(t).
The amplitude is 6 and the maximum value is y = 3.
The amplitude is 3 and the maximum value is y = 6.
The amplitude is 6 and the maximum value is y = 6.
The amplitude is 3 and the maximum value is y = 3.


Math
TrigonometrySolve the triangle, if possible. Round to the nearest hundredth.
a = 27 ft
b = 31 ft
c = 42 ft
A = 39.96°, B = 47.51°, C = 92.53°
A = 39.96°, B = 23.76°, C = 116.28°
A= 47.51°, B = 39.96°, C.= 92.53°
No solution

Math
TrigonometryAn airplane ascends at an angle of elevation of 22" for a ground distance of 7850 feet. What height does the plane gain during this ascent? Draw a picture on paper to support your answer, and round your answer to the nearest whole foot.
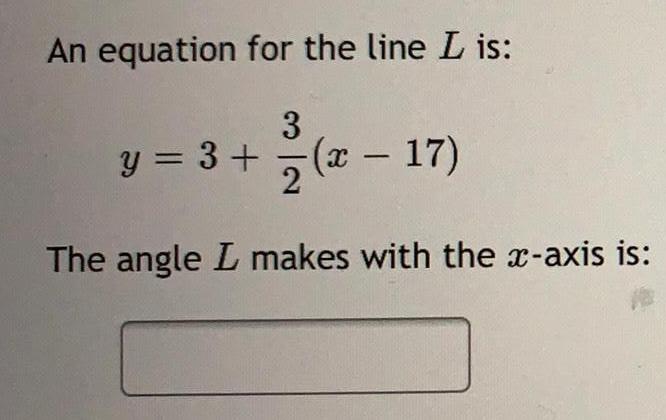
Math
TrigonometryAn equation for the line L is:
y = 3 + 3/2 (x - 17)
The angle L makes with the x-axis is:

Math
TrigonometryThe height of a vertical cliff is 450 meters. The angle of elevation from a ship to the top of the cliff is 23°. The ship is x meters from the bottom of the cliff.
Draw a diagram to show this information, then solve for x.

Math
TrigonometryA construction worker leans a ladder against a building. The ladder is 27 ft long and the distance between the base of the ladder and the bottom of the building is 9 ft. Find the angle formed between the ground and the base of the ladder.


Math
TrigonometryFor the given function, state the amplitude and the minimum output for the function:
f(t)= 3cos (t+π/6)
The amplitude is 3 and the minimum output value is y=-3.
The amplitude is 3 and the minimum output value is y=-π/6
The amplitude is π/6 and the minimum output value is y=-3
The amplitude is π/6 and the minimum output value is y=-π/6

Math
Trigonometry#35. Find the measure of the angle of elevation of the Sun when a pole 32 feet tall casts a shadow that is 53 feet long.
(Hint: Draw and Label a right triangle)
A 37.14
B 58.88
C 31.12
D 52.86

Math
TrigonometryLet θ be an angle such that csc0= 7/4 and tanθ <0.
Find the exact values of cotθ and cosθ.
Math
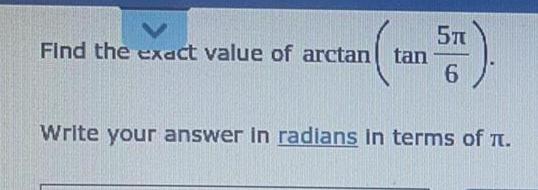
TrigonometryFind the exact value of arctan (tan5π/6)
Write your answer in radians in terms of π.
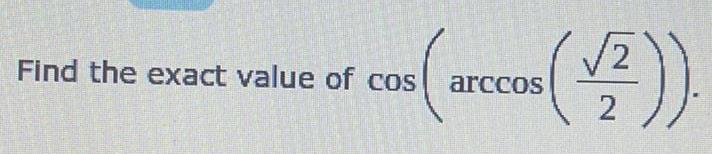

Math
TrigonometryLet 8 be an angle such that tanθ=2/3 and cscθ>0.
Find the exact values of sin θ and secθ
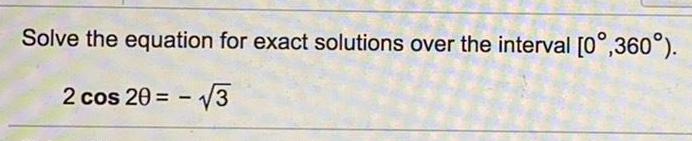
Math
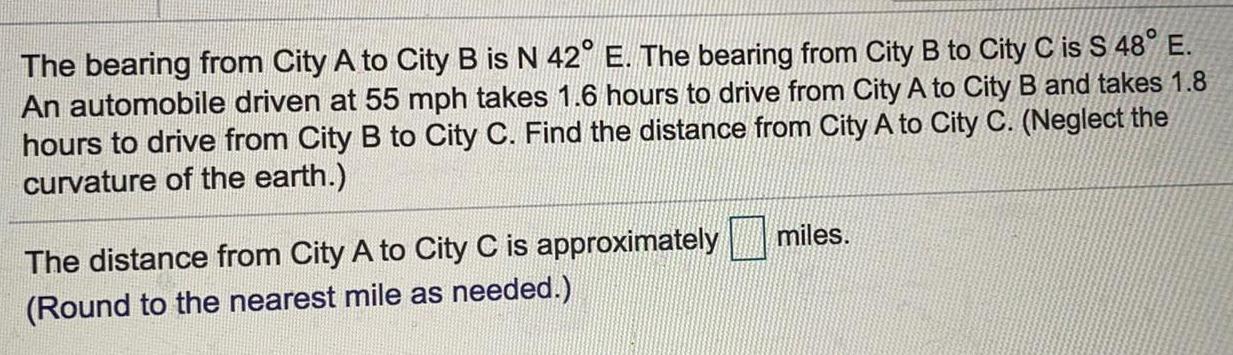
TrigonometryThe bearing from City A to City B is N 42° E. The bearing from City B to City C is S 48° E.
An automobile driven at 55 mph takes 1.6 hours to drive from City A to City B and takes 1.8
hours to drive from City B to City C. Find the distance from City A to City C. (Neglect the
curvature of the earth.)
The distance from City A to City C is approximately
(Round to the nearest mile as needed.)
miles.

Math
TrigonometryThis is an excerpt from a 1935 sermon by Father Charles Coughlin. In this context of this paragraph, what does the word assailed mean?
A) to attack with physical force
B) to leave for another location
C) to enter into a written contract
D) to attack with criticism and ridicule

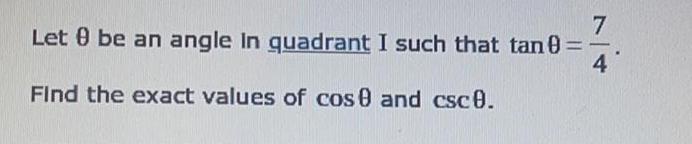
Math
TrigonometryLet θ be an angle in quadrant I such that tan θ=7/4
Find the exact values of cos θ and csc θ

Math
TrigonometryA 75-horsepower outboard motor at full throttle will rotate its propeller at exactly 4100 revolutions per min. Find the angular speed of the propeller in radians per second.

Math
TrigonometryIf 0= 135°, find the exact value of each expression below.
(a) cos (-θ) = 1
(b)cos ²θ=
(c) cos 2θ = .0
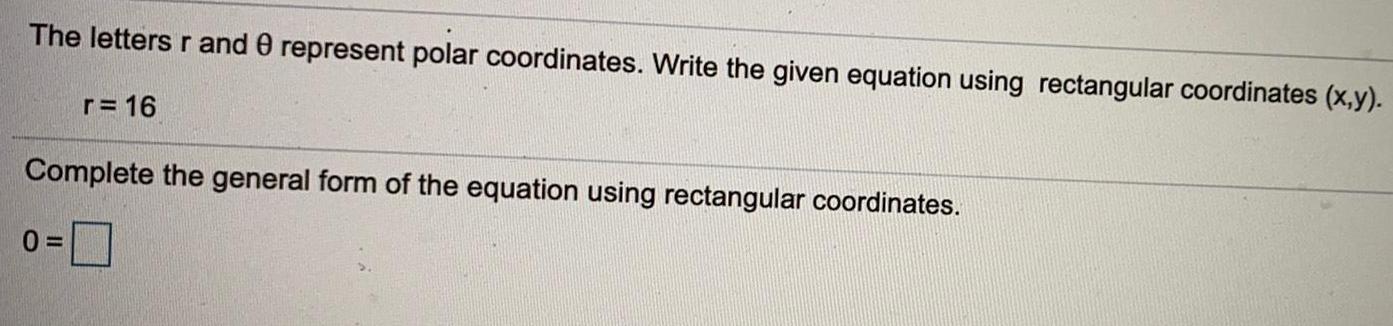
Math
TrigonometryThe letters r and θ epresent polar coordinates. Write the given equation using rectangular coordinates (x,y).
r = 16
Complete the general form of the equation using rectangular coordinates.
0=

Math
TrigonometryFind the exact value of cos(u + v) given that sin u =4/5 with u in quadrant II, and sin v=12/13 with v in the quadrant II.
(Simplify your answer. Type an integer or a simplified fraction.)
cos (u + v) =

Math
TrigonometryA guy wire to the top of a tower makes an angle of 66° with the level ground. At a point 30 feet farther from the base of the tower and in line with the base of the wire, the angle of elevation to the top of the tower is 29°. What is the length of the guy wire?
24.17 ft
15.92 ft
56.53 ft
45.54 ft

Math
TrigonometryIdentify and graph the polar equation.
r=7-7 sin θ
What shape does the polar equation form when graphed?
A. Limacon without an inner loop.
C. Limacon with an inner loop.
B.Cardioid that is symmetric to line θ =π/2
D. Cardioid that is symmetric to the polar axis.

Math
TrigonometryUse the power reducing formulas to rewrite cos44x in terms of the first power of cosine.
Simplify your answer as much as possible.
To indicate your answer, first choose one of the four forms below.


Math
TrigonometryA building is 60 feet high. At a distance away from the building, an observer notices that the angle of elevation to the top of the building is 41°. How far is the observer from the base of the building?
79.5 ft
69.0 ft
52.2 ft
91.5 ft

Math
TrigonometryUse a sum or difference identity to find the exact value of the expression.
tan 15°
tan 15° =
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)

Math
TrigonometryTyler stands at the top of a 40 meter tall vertical cliff. Down below, Susie stands some distance away from the base of the cliff. Tyler's angle of depression to Susie is 34°. How far is Susie from the base of the cliff? Round answer to the nearest tenth. You must draw the picture to represent the situation. (3 pts)

Math
Trigonometrycan write trigonometric ratios of a right triangle, using my understanding of the Pythagorean theorem and special right triangles.
If tan θ = 12/5 , what does cos θ =?
5/13
12/13
5/12
12/5
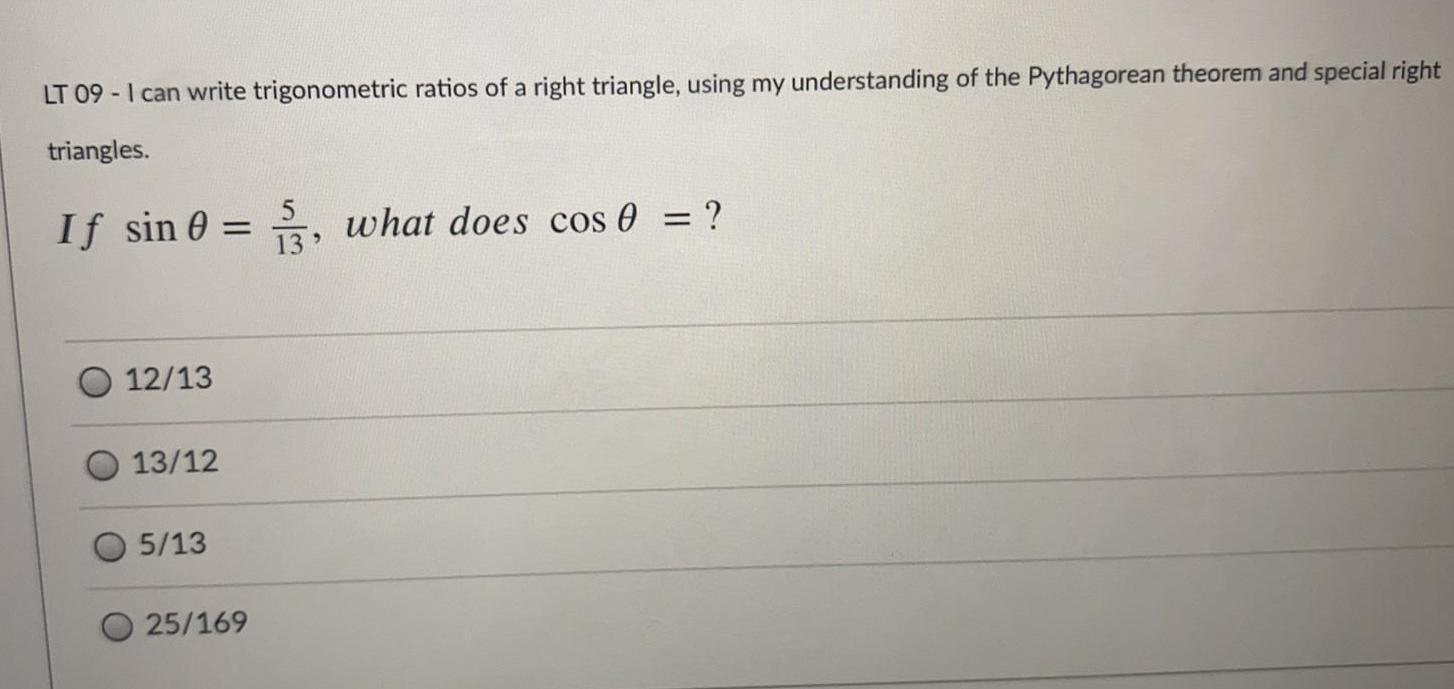
Math
TrigonometryI can write trigonometric ratios of a right triangle, using my understanding of the Pythagorean theorem and special right
triangles.
If sin θ = 5/13, what does cos θ = ?
12/13
13/12
5/13
25/169
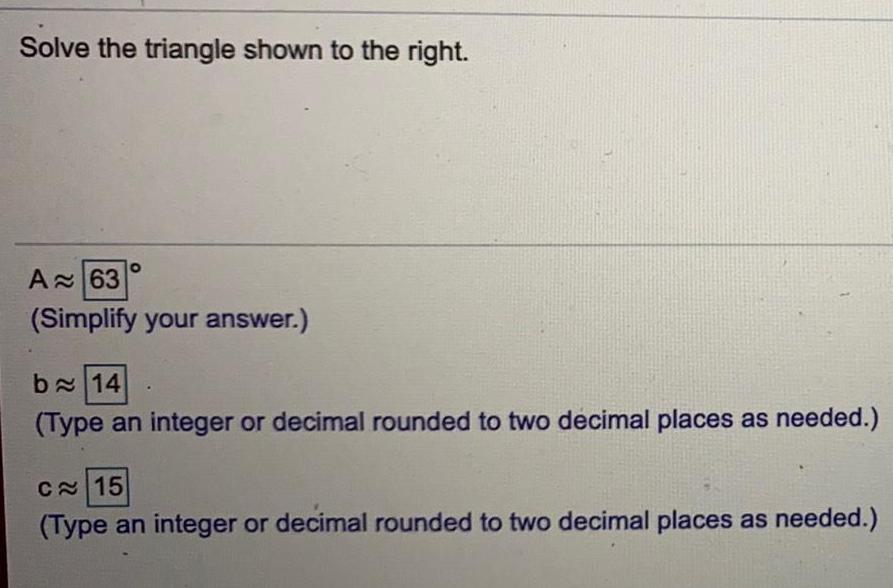
Math
TrigonometrySolve the triangle shown to the right.
A≈
(Simplify your answer.)
b≈
(Type an integer or decimal rounded to two decimal places as needed.)
C
(Type an integer or decimal rounded to two decimal places as needed.)
Math
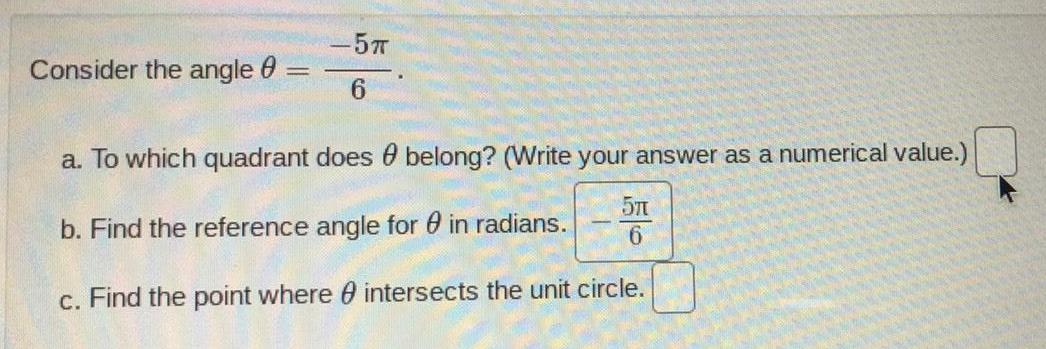
TrigonometryConsider the angle θ=-5π/6
a. To which quadrant does belong? (Write your answer as a numerical value.)
b. Find the reference angle for in radians
c. Find the point where intersects the unit circle.

Math
Trigonometry5/6. From the outside the weightroom, Drake sees Cade walking at the track. If the height of the track stairs is 30 feet from the bottom to the top, and Drake is 35 feet from the bottom of the stairs, what is the angle of elevation fom Drake to the track? Round to the nearest 10th.
Picture
Equation:
Answer:

Math
TrigonometryThe angle of elevation to the top of Wayne Tower in Gotham City is found to be 11° from the ground at a distance of 5,280 feet from the
base of the building. Using this information, find the height of Wayne Tower.
The height of Wayne Tower is
feet. Round your answer to the nearest tenth of a foot.
. Note that for this problem, we are using degrees to measure angles. Make sure your calculator is set to degrees instead of radians.
Math
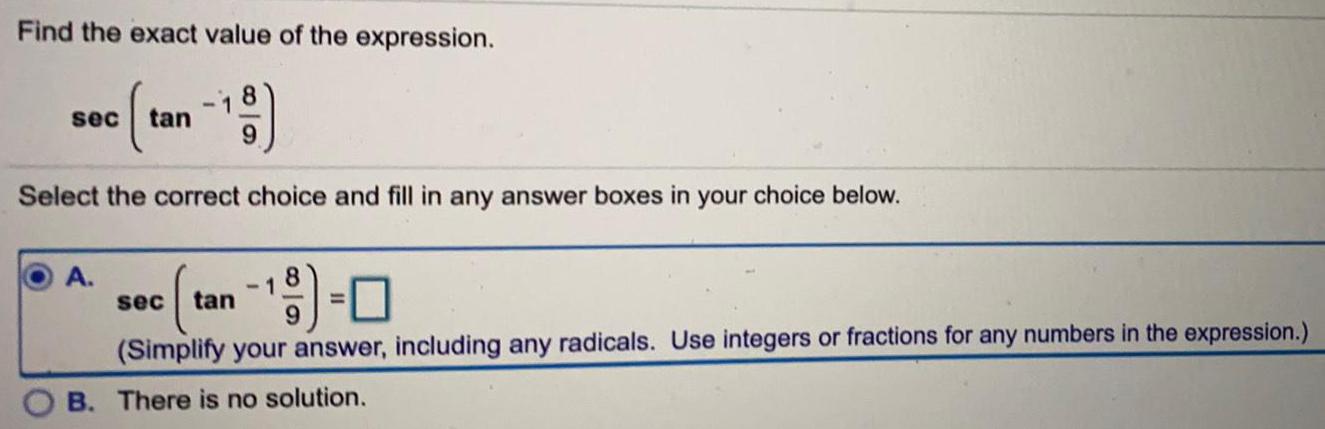
TrigonometryFind the exact value of the expression.
sec ( tan^-1 (8/9) =
Select the correct choice and fill in any answer boxes in your choice below.
A. sec ( tan^-1 (8/9) =
B. There is no solution.

Math
TrigonometryUse your calculator to find the angle measures sin-¹ (0.7), cos¯¹(0.3), and tan-¹ (38.4) to the nearest tenth of a degree.
a. sin-¹(0.7) = 0.8° , cos-¹(0.3) = 1.3° , tan-¹(38.4) = 1.5°
b. sin-¹ (0.7) = 1.3°, cos-¹ (0.3) = 0.8°, tan-¹ (38.4) = 1.5°
c. sin-¹ (0.7) = 44.4°, cos-¹(0.3) = 72.5° , tan-¹ (38.4) = 88.5°
d. sin-¹ (0.7) = 72.5°, cos-¹(0.3) = 44.4°, tan-¹ (38.4) = 88.5°

Math
TrigonometryOrlando and Ryan are taking measurements related to the installation of a TV tower. Orlando measures a 62° angle of elevation to the top of the 950 ft TV tower. Find the angle of elevation for Ryan, standing 80 ft farther from the tower than Orlando. Round answer to nearest tenth.

Math
TrigonometrySolve the following problem. Be sure to make a diagram of the situation with all the given information labeled.
A 72.7-foot rope from the top of a circus tent pole is anchored to the ground 44.3 feet from the bottom of the pole. What angle does the rope make with the pole?
(Assume the pole is perpendicular to the ground. Round your answer to one decimal place.)

Math
TrigonometryA ship left the bay and has sailed toward 30 degrees to the east for 5 km. If we set the
bay to be the origin and the north to be the y-axis direction, and the east to be the x-direction,
what is the coordinate of the ship now?

Math
TrigonometryA slide on a playground rises at a 45° angle. The top of the slide is 20 feet above the ground. How far does a child travel down the silde? Round answer to the nearest hundredth place.
34.64 feet
40.00 feet
20.00 feet
28.28 feet

Math
TrigonometryThe point (1, -1) is on the terminal side of angle 8, in standard position. What are the values of sine, cosine, and tangent of θ? Make sure to show all work.