Trigonometry Questions and Answers

Math
TrigonometryThe largest Egyptian pyramid is 146.5 m high. When Rowena stands far away from the pyramid, her line of sight to the top of the pyramid forms an angle of elevation of 20° with the ground. What is the horizontal distance between the center of the pyramid and Rowena? Round to the nearest meter.

Math
TrigonometryA dolphin is jumping in the ocean and makes a leap out of the water. The dolphin leaves
the water traveling at a speed of 32 ft/sec and an angle of 48° with the surface of the
water. How far horizontally across the water does the dolphin travel?

Math
TrigonometryIn a tourist bus near the base of Eiffel Tower at Paris, a passenger estimates the angle of elevation to the top of the tower to be 60°. If the height of Eiffel Tower is about 984 feet, what is the distance from the bus to the base of the tower?

Math
TrigonometryA bird is sitting on top of a statue. From a point that is 42 feet away from the statue, the angle of elevation is measured to be 16°. Find
the height of the statue.
Your answer is
feet. Round your answer to the nearest whole number.

Math
TrigonometrySheena claims that all quadrilaterals are rectangles. Which of the statements below disproves Sheena's claim?
Quadrilaterals have four sides.
Quadrilaterals are polygons.
A square is a quadrilateral.
A trapezoid is a quadrilateral.
Math
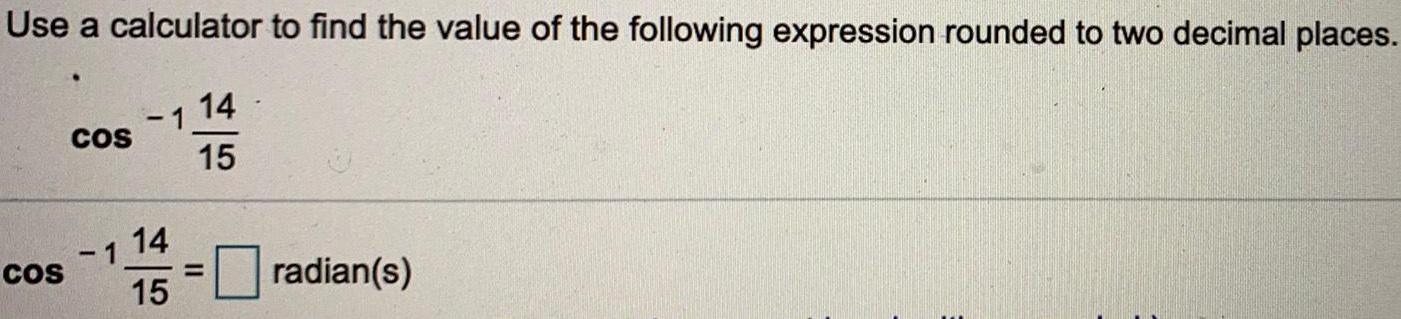
TrigonometryUse a calculator to find the value of the following expression rounded to two decimal places.
cos -1 14/15

Math
TrigonometryA surveyor is measuring the height of a building from a sidewalk two meters away from the building. The angle of elevation from the surveyor's eye to the top of the building is 74.393° and the angle of depression from the surveyor's eye to the base of the building is 40.030°. How tall is the building?
2 tan(114.423°) meters
(74.393) (40.030) sin(2) meters
2 (sin(74.393°) + sin(40.030°)) meters
2 (tan (74.393°) + tan(40.030°)) meters
2 + tan(74.393°) meters
Math
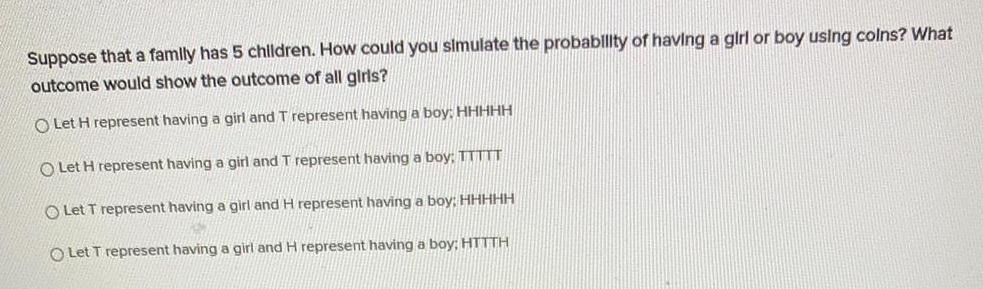
TrigonometrySuppose that a family has 5 children. How could you simulate the probability of having a girl or boy using colns? What outcome would show the outcome of all girls?
Let H represent having a girl and T represent having a boy: HHHHH
Let H represent having a girl and T represent having a boy: TTTTT
Let T represent having a girl and H represent having a boy; HHHHH
Let T represent having a girl and H represent having a boy: HTTTH

Math
TrigonometryA resistor and an inductor connected in a series network impede the flow of an alternating current. This impedance Z is determined by the reactance X of the inductor and the resistance R of the resistor. The three quantities, all measured in ohms, can be represented by the sides of a right triangle as illustrated, so Z² = x² + R². The angle is called the phase angle. Suppose a series network has an inductive reactance of X=400 ohms and a resistance of R = 1000 ohms.
(a) Find the impedance Z.
(b) Find the values of the six trigonometric functions of the phase angle .
![What is the estimate of the area under the curve of f using rectangular approximations and sample points on the interval [-1.5, 1.5]?
Evaluate the function at:
x = -1.3 on [-1.5, -1]
x= -0.7 on [-1,0]
x = 0.7 on [0, 1]
x = 1.3 on [1, 1.5]](https://media.kunduz.com/media/sug-question/raw/46494481-1658300822.1040146.jpeg?w=256)
Math
TrigonometryWhat is the estimate of the area under the curve of f using rectangular approximations and sample points on the interval [-1.5, 1.5]?
Evaluate the function at:
x = -1.3 on [-1.5, -1]
x= -0.7 on [-1,0]
x = 0.7 on [0, 1]
x = 1.3 on [1, 1.5]

Math
TrigonometryDraw triangle JKL with right angle L. If Sin J = 8/17, find each of the following ratios.
Give answers in fraction form.
Cos J=
Tan J =
Sin K =
Cos K =
Tan K =
Math
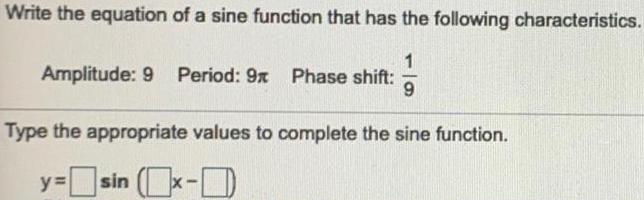
TrigonometryWrite the equation of a sine function that has the following characteristics.
Amplitude: 9 Period: 9π Phase shift: 1/9
Type the appropriate values to complete the sine function.
y=sin(x-)

Math
TrigonometryA triangular plot of land has one side along a straight road measuring 289 feet. A second side makes a 62° angle with the road, and the third side makes a 56° angle with the road. How long are the other two sides?
The longer side of the triangular plot is feet. The shorter side of the triangular plot is feet.
(Round to the nearest hundredth as needed.)
Math
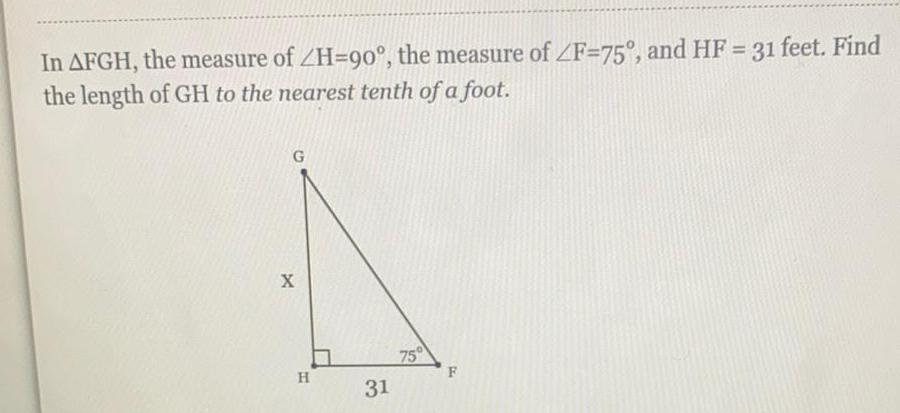
TrigonometryIn ΔFGH, the measure of ∠H-90°, the measure of ∠F=75°, and HF = 31 feet. Find
the length of GH to the nearest tenth of a foot.
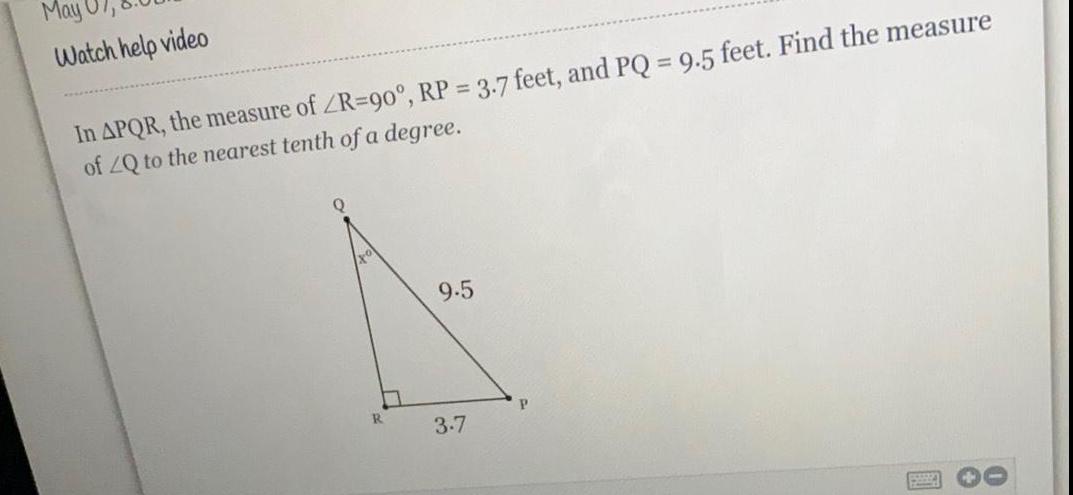
Math
TrigonometryIn ΔPQR, the measure of ∠R-90°, RP = 3.7 feet, and PQ = 9.5 feet. Find the measure of ∠Q to the nearest tenth of a degree.
Math
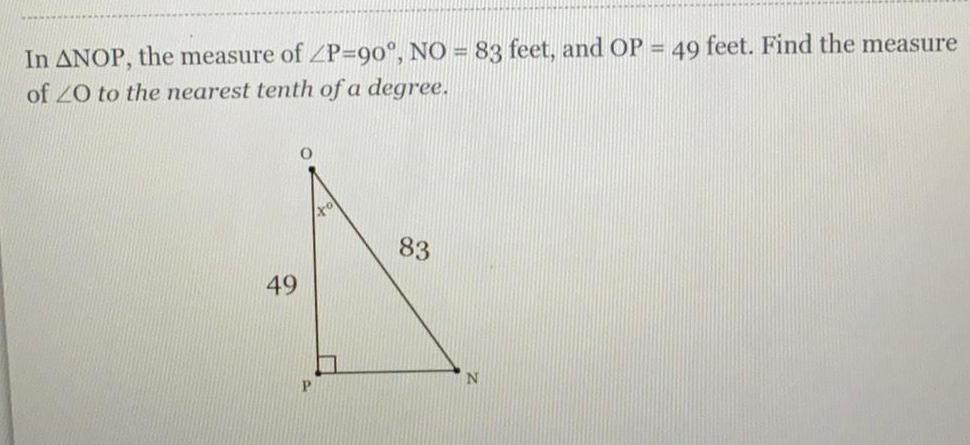
TrigonometryIn ΔNOP, the measure of ∠P-90°, NO = 83 feet, and OP = 49 feet. Find the measure of ∠0 to the nearest tenth of a degree.

Math
TrigonometryT
If sin 0= 77,0 <0</2₁
7,0<8<,
(a) sin (20)
find the exact value of each of the following.
(b) cos (20)
7|2
0
(c) sin
(c) sin 2
(a) sin (20) =
12√13
49
(Type an exact answer, using radicals as needed.)
-23
(b) cos (20) =
49
(Type an exact answer, using radicals as needed.)
0
2
(Type an exact answer, using radicals as needed.)
-
(d) cos 2
Math
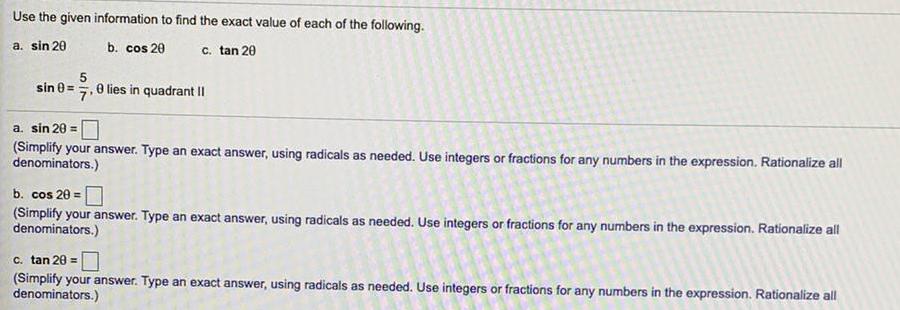
TrigonometryUse the given information to find the exact value of each of the following.
a. sin 20
b. cos 20
c. tan 20
sinθ=5/7, θ lies in quadrant II
a. sin 20 =
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression. Rationalize all
denominators.)
b. cos 20 =
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression. Rationalize all
denominators.)
c. tan 20 =
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression. Rationalize all
denominators.)

Math
TrigonometryHow long is a ladder that reaches a height of 4.36 m up a wall and rests on the wall at an angle of elevation of 74°? Hint: Be sure to draw a picture
a. 4.54 m
b. 15.82 m
c. 3.24 m
d. 1.25 m

Math
TrigonometryFrom the top of a lighthouse 210 feet high, the angle of depression of a boat is 27°. Find the horizontal distance from the boat to the foot of the lighthouse. The lighthouse was built at sea level.

Math
TrigonometryGiven tan A = 12/5 and that angle A is in Quadrant I, find the exact value of sin A in simplest radical form using a rational denominator.
Math
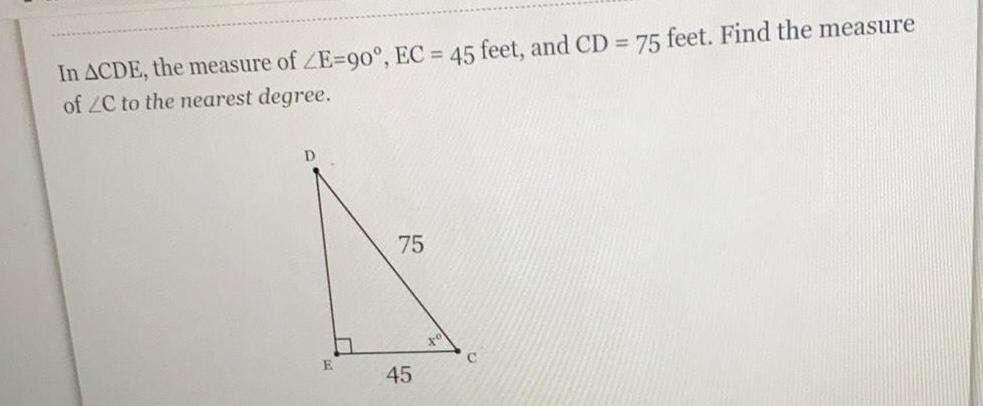
TrigonometryIn ΔCDE, the measure of ∠E=90°, EC = 45 feet, and CD = 75 feet. Find the measure
of ∠C to the nearest degree.

Math
TrigonometryFind the exact value of cos π/3, expressing your answer with a rational denominator.
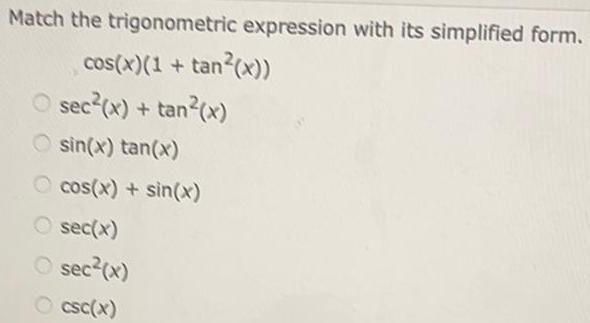
Math
TrigonometryMatch the trigonometric expression with its simplified form.
cos(x)(1+ tan²(x))
sec²(x) + tan²(x)
sin(x) tan(x)
cos(x) + sin(x)
sec(x)
sec²(x)
csc(x)

Math
TrigonometryA) Find the exact value for each, given the information.
B) In which quadrant is the angle (a + B)?
sin a = -4/5 and cos b = 12/13 ; a & ß are in the same quadrant. Find sin(a +b) and cos(a + b).
sin a = 8/17 and cos b = 7/25 ; a & ß are in the same quadrant. Find sin(a +b) and cos(a + b).

Math
TrigonometryA hot-air balloon is floating above a straight road. To calculate their height above the ground, the balloonists simultaneously measure the angle of depression to two consecutive mileposts on the road on the same side of the balloon. The angles of depression are found to be 21 and 23°. How high (in feet) is the ballon?

Math
TrigonometryYou are flying a kite on a line that is 350 feet
long. Let's suppose the line is perfectly straight
(it never really is) and it makes an angle of 65
degrees with the horizontal direction. The kite is
flying at an altitude of feet.
Hint: Draw a picture. Look for a right triangle.

Math
TrigonometryTo be used safely, a ladder should make no more than a 70° angle with the ground. What is the maximum height a 32 ft ladder can reach? Round answer to the nearest tenth
Max height=

Math
TrigonometryEvaluate (if possible) the six trigonometric functions of the real number t. (If an answer is undefined, enter UNDEFINED.)
t = 7π/4

Math
TrigonometryEvaluate (if possible) the sine, cosine, and tangent at the real number t. (If an answer is undefined, enter UNDEFINED.)
t=-11π/6

Math
TrigonometryA wire is tied from the top of a telephone pole to a stake in the ground. If the stake is 12 ft from the bottom of the pole and the wire makes a 78° angle with the ground, how long is the wire? Round your answer to the nearest tenth.

Math
Trigonometry3. Mr. Jones observes that the angle of elevation to the top of a nearby building is 41.5°. After moving back a distance of 265 feet from the building, he finds that the angle of elevation to the top of the building is now 21.6°. Find the height of the building.

Math
TrigonometryA ship leaves the Boston Harbor and travels at a bearing of 52° for 200 miles and then changes course and travels for an additional 80 miles at a bearing of 142° to an island location.
a). How far is the ship from the Harbor?
b) If the ship is able to return home on a direct route from the island to the Harbor, at what bearing
should the ship travel?

Math
TrigonometryJacksonville, Florida is due south of Charleston, West Virginia. Find the distance between Jacksonville (30°20') and Charleston (38°21'). Assume that the radius of the Earth is 3960 miles. Round your answer to the nearest whole mile. The distance is miles.

Math
TrigonometryThe rod on a pump rises and falls as the pump operates. Function /gives the height of the top of the rod above the pumping unit in feet, L(t), as a function of time in seconds, t, after the pump is activated.
L(t) = sin(πt +π/2 ) + 3/2
What is the range of the given function?
A. 0 feet to 3 feet
B. 0 feet to feet
C. 1-foot to feet
D. 1 foot to 3 feet

Math
TrigonometryThe average monthly temperature, T, in degrees Celsius, for any month m, for the town of Someplace, is modeled by the function T(m) = 19.1 sin(3π/9 x) + 7.5.
a. What is the period of the function and what does it mean?
b. Plot one full cycle of the function below. Show all of your thinking work and be sure to label your axes correctly.
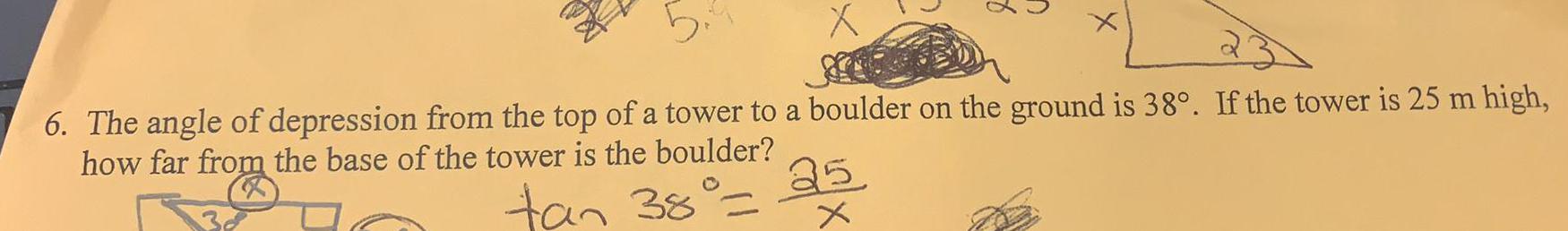
Math
TrigonometryThe angle of depression from the top of a tower to a boulder on the ground is 38°. If the tower is 25 m high, how far from the base of the tower is the boulder?
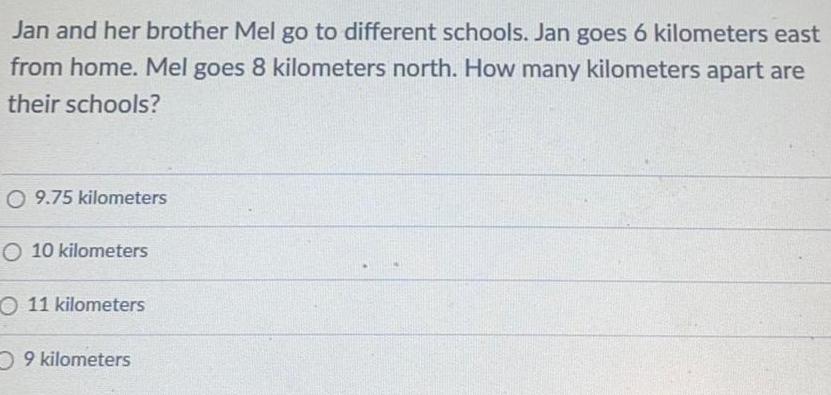
Math
TrigonometryJan and her brother Mel go to different schools. Jan goes 6 kilometers east from home. Mel goes 8 kilometers north. How many kilometers apart are their schools?
9.75 kilometers
10 kilometers
11 kilometers
9 kilometers

Math
TrigonometryTwo ships leave the same port at the same time. The Explorer is traveling at a bearing of N 17° W at
43 miles per hour and the Adventurer is traveling at a bearing of S 73° W at 37 miles per hour.
a) How far apart are the two ships after 3 hours of travel?
b) If the ships lay anchor after three hours and a small boat travels directly from The Explorer to the
Adventurer, at what bearing should the boat travel?


Math
TrigonometryA skyscraper is 396 meters tall. At a certain time of day, it casts a shadow that is 332 meters long. At what angle is the sun above the horizon at that time?
A 57⁰
B. 50⁰
C. 40⁰
D. 33°

Math
TrigonometryUse a symmetry test to determine which of the following equations demonstrate θ = symmetry. Select all that apply.
Select all that apply:

Math
TrigonometryFind the exact value of sinπ/12 using the half-angle identity. Support your answer with a calculator approximation.

Math
TrigonometryAirports A and B are 462 km apart, on an east-west line. Jim flies in a northeast direction from A to airport C. From C he flies 353 km on a bearing of 129°20' to B. How
far is C from A?
The distance between C and A is km.
(Round to the nearest kilometer as needed.)


Math
TrigonometryA particular sound wave can be graphed using the function y = sin4x. Find the amplitude and period of the function.
a. amplitude = 1, period= (1/2)p
b. amplitude = 2p, period=-1
c. amplitude = (1/2)p, period = 1
d. amplitude = -1, period = 2
Please select the best answer from the choices provided
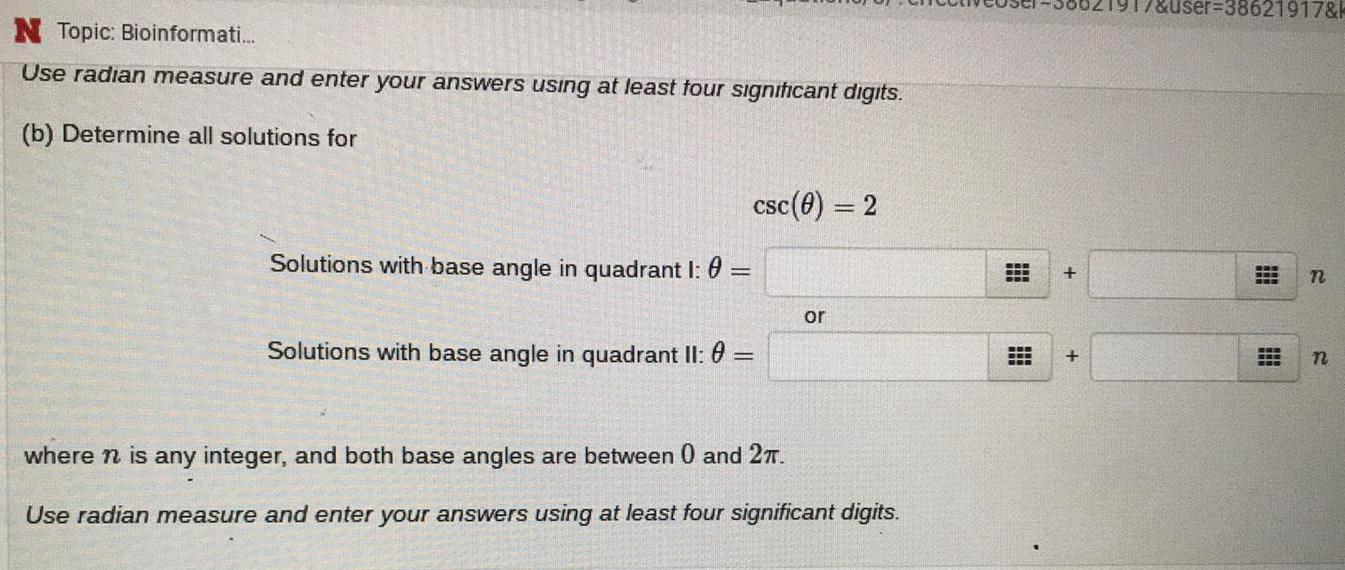
Math
TrigonometryUse radian measure and enter your answers using at least four significant digits.
(b) Determine all solutions for csc(θ)=2
Solutions with base angle in quadrant I: θ=
Solutions with base angle in quadrant II: θ=
where n is any integer, and both base angles are between 0 and 2π
Use radian measure and enter your answers using at least four significant digits.

Math
TrigonometryThe Cartesian coordinates of a point are given.
(a) (-7,7)
(i) Find polar coordinates (r, θ) of the point, where r> 0 and 0 ≤ θ< 2π
(r,θ) =
(ii) Find polar coordinates (r, θ) of the point, where r < 0 and 0 ≤ θ< 2π
(r, θ) =
(b) (2,2√3)
Find polar coordinates (r, 8) of the point, where r> 0 and 0 ≤ θ < 2π.
(r, θ) =
(ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 ≤ θ < 2π.
(r, θ) =
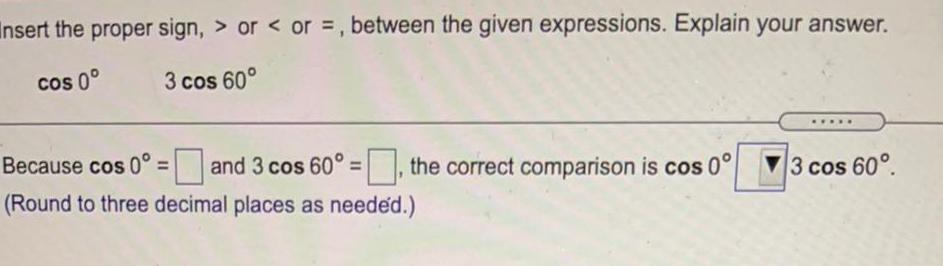
Math
TrigonometryInsert the proper sign, > or < or =, between the given expressions. Explain your answer.
cos 0° 3 cos 60°
Because cos 0° = and 3 cos 60° =, the correct comparison is cos 0° 3 cos 60°.
(Round to three decimal places as needed.)

Math
TrigonometryGiven that the point (160, -36) is on the terminal side of an angle, θ, find the exact value of the following:
sin(θ)=
cos(θ)=
tan(θ)=
csc (θ)=
sec (θ)=
cot (θ)=