Basic Math Questions and Answers

Math
Basic MathA vector with magnitude 6 points in a direction 295 degrees counterclockwise from the positive x axis.
Write the vector in component form.
Vector =
Give each value accurate to at least 1 decimal place
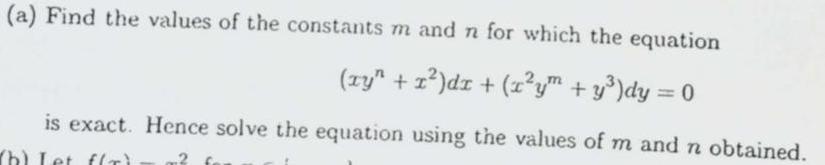
Math
Basic Math(a) Find the values of the constants m and n for which the equation
(xy² + x²)dx + (x²y + y³)dy = 0
is exact. Hence solve the equation using the values of m and n obtained.
(b) Let f(r) 2

Math
Basic MathIan's investment in his savings account matured to $5,510.89 at the end of 135 days. If
the account was earning simple interest at a rate of 1.50% p.a., answer the following.
a. What was Ian's initial investment?
$0.00
Round to the nearest cent
Math
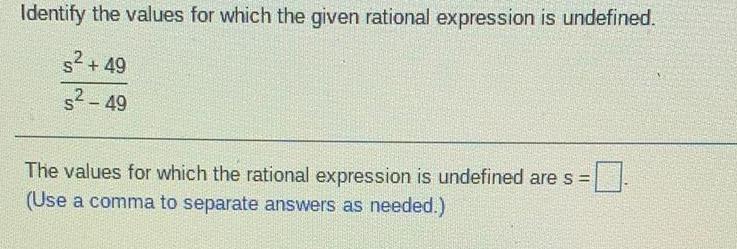
Basic MathIdentify the values for which the given rational expression is undefined.
s²+49
52-49
The values for which the rational expression is undefined are s =
(Use a comma to separate answers as needed.)

Math
Basic MathIf an object is projected upward with an initial velocity of 127 ft per sec, its height h after t seconds is h=-161²2 + 127t. Find the height of the object after 4 seconds.
The height of the object after 4 seconds is
(Simplify your answer.)
ft.
DOE
Math
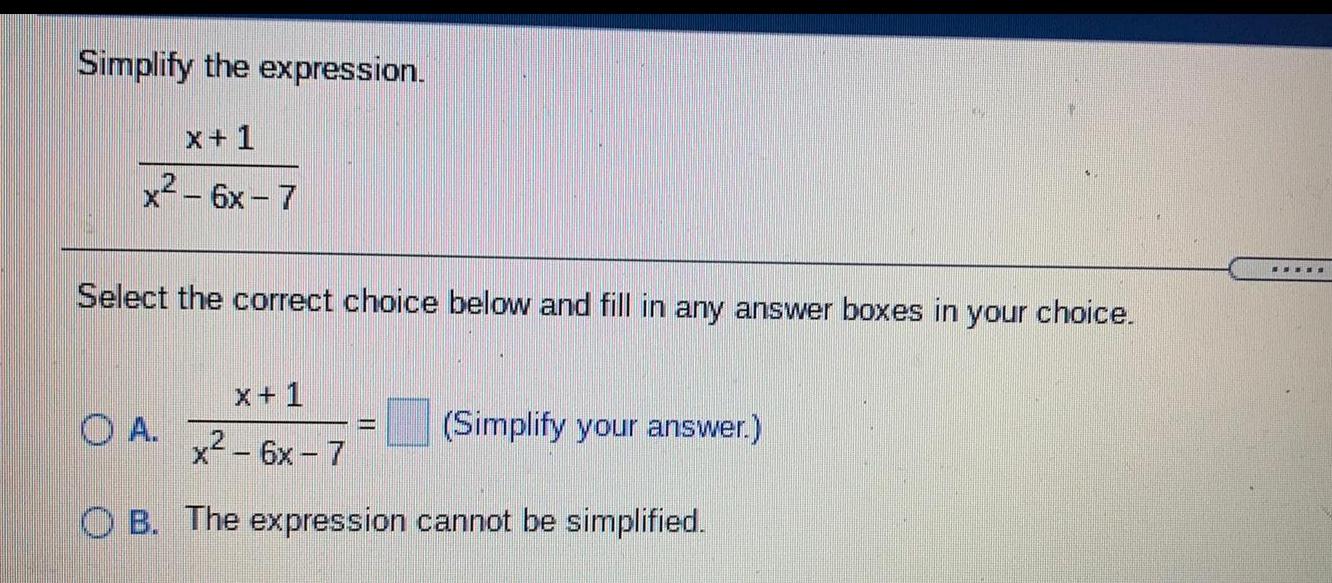
Basic MathSimplify the expression.
x+1
x² - 6x - 7
Select the correct choice below and fill in any answer boxes in your choice.
x + 1
x² - 6x - 7
OB. The expression cannot be simplified.
OA.
(Simplify your answer.)
*****

Math
Basic MathThis, and Esther) form a club, N={A, B, C, D, E). Callie and Esther are women, and the others are men. If they choose a secretary randomly, fir
the odds against a person whose name begins with a vowel becoming secretary.
The odds against a person whose name begins with a vowel becoming secretary are
(Type whole numbers.)
to
0

Math
Basic MathA parabola is the set of all points P in the plane that are equidistant from a fixed line called the
A parabola is the set of all points P in the plane that are equidistant from a fixed line called the
and a fixed point not on the line called the
and a fixed point not on the line called the

Math
Basic Math8. Louis wants to take out a $14,000 loan with a 6.8% APR. He can afford to pay
no more than $400 per month for loan payments. What would be the length
of his loan? Round to the nearest tenth of a year.

Math
Basic MathAs Jupiter revolves around the sun, it travels at a speed of approximately 8 miles per second. Convert this
speed to kilometers per second. At this speed, how many kilometers will Jupiter travel in 2 seconds? In your
computations, assume that I mile is equal to 1.6 kilometers. Do not round your answers.
Speed:
Distance traveled in 2
seconds:
km
X 5
?
Math
Basic MathASK YOUR TEACHER
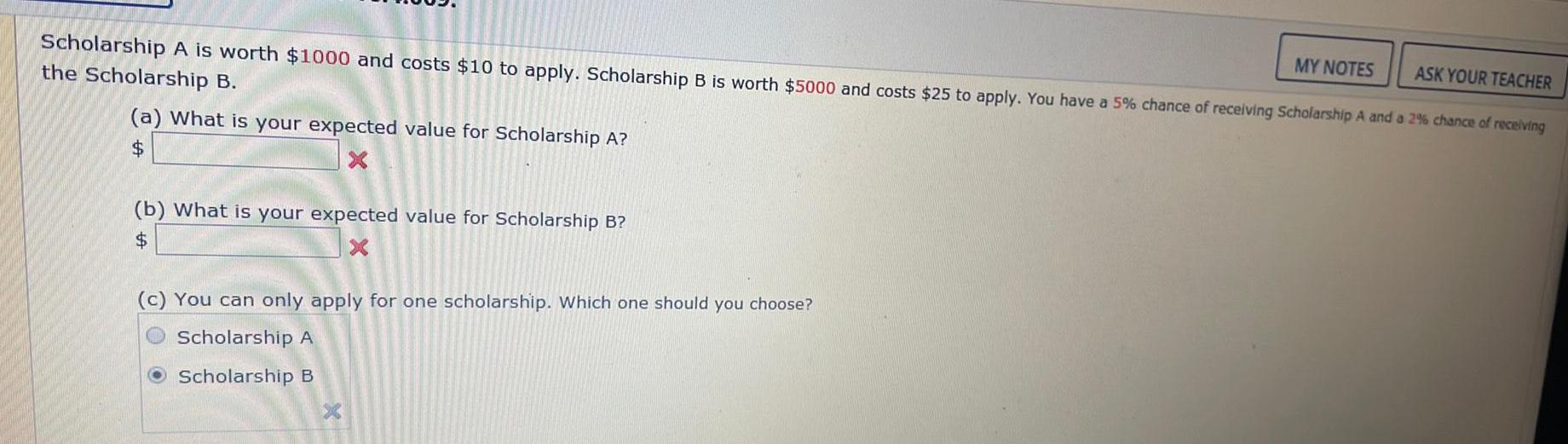
Scholarship A is worth $1000 and costs $10 to apply. Scholarship B is worth $5000 and costs $25 to apply. You have a 5% chance of receiving Scholarship A and a 2% chance of receiving
the Scholarship B.
(a) What is your expected value for Scholarship A?
$
X
(b) What is your expected value for Scholarship B?
$
X
(c) You can only apply for one scholarship. Which one should you choose?
Scholarship A
Scholarship B
MY NOTES
Math
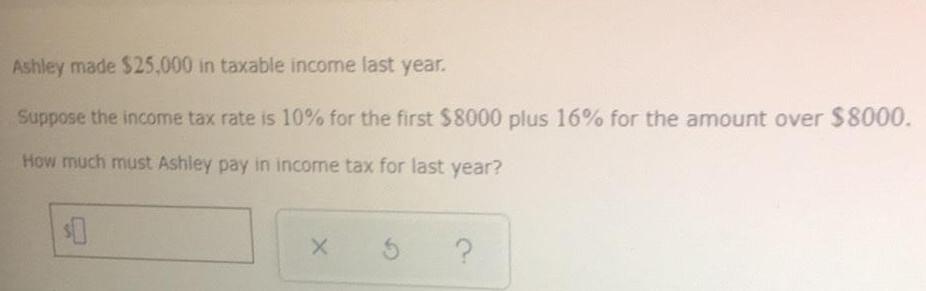
Basic MathAshley made $25,000 in taxable income last year.
Suppose the income tax rate is 10% for the first $8000 plus 16% for the amount over $8000.
How much must Ashley pay in income tax for last year?
X
5
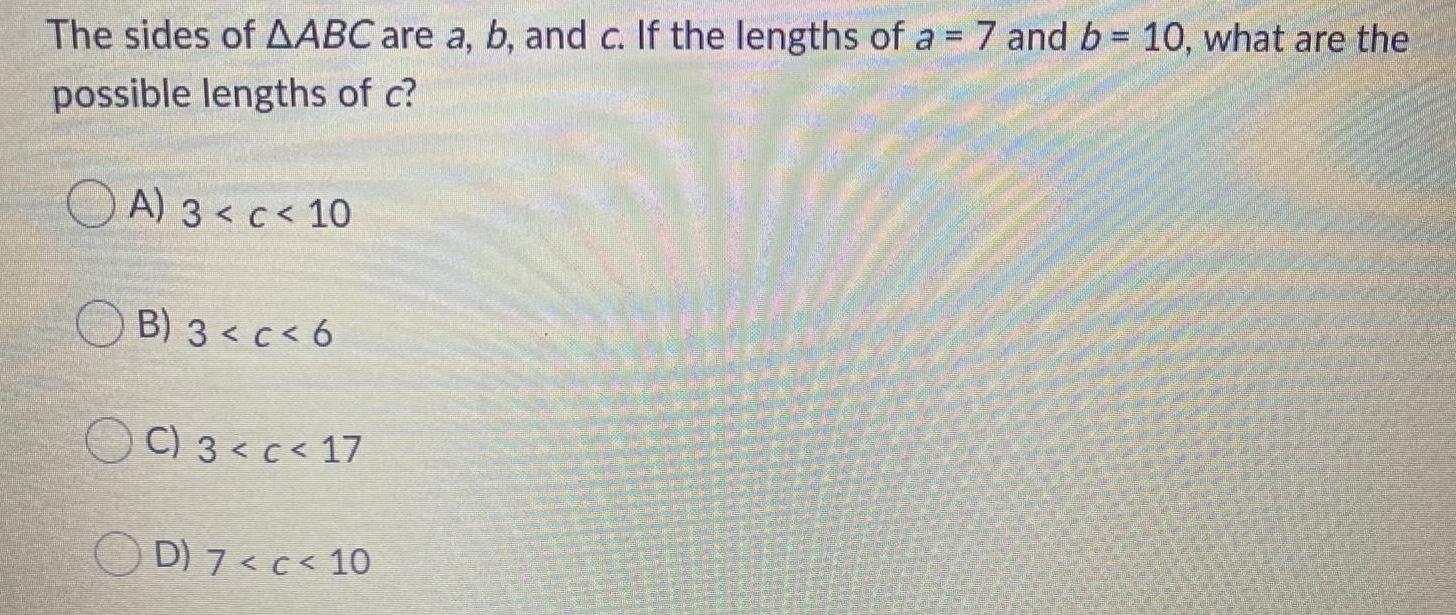
Math
Basic MathThe sides of AABC are a, b, and c. If the lengths of a = 7 and b= 10, what are the
possible lengths of c?
A) 3 < c < 10
B) 3<c< 6
C) 3 < c < 17
D) 7 < c < 10
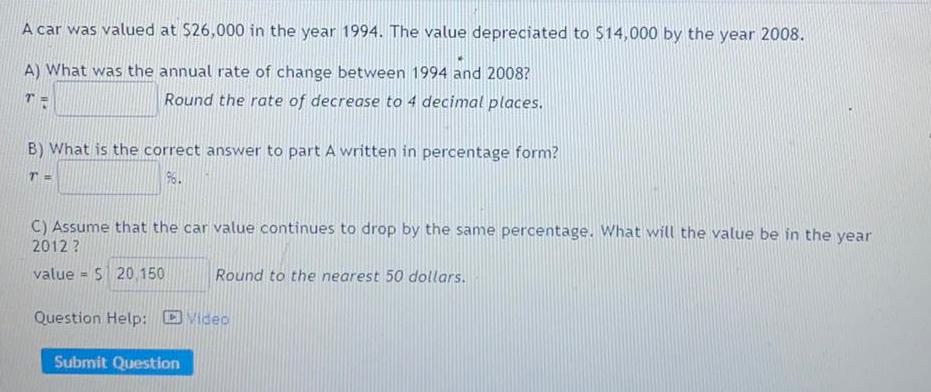
Math
Basic MathA car was valued at $26,000 in the year 1994. The value depreciated to $14,000 by the year 2008.
A) What was the annual rate of change between 1994 and 2008?
TR
Round the rate of decrease to 4 decimal places.
B) What is the correct answer to part A written in percentage form?
T=
96.
C) Assume that the car value continues to drop by the same percentage. What will the value be in the year
2012?
Round to the nearest 50 dollars.
value $ 20,150
=
Question Help: Video
Submit Question

Math
Basic MathA total of 120 high school students were surveyed about their winter break shopping habits. The results revealed that 45% shop for new clothes, 55% shop for school
supplies, and 35% shop for clothes and school supplies. How many students shop for clothes or school supplies over the break?
The number of students who shopped for clothes or school supplies over the break is

Math
Basic MathHow long will it take for an investment of $1000 to double in value if the interest rate is 8.5% per year, compounded continuously? (Round your answer to two decimal places.)
yr
Math
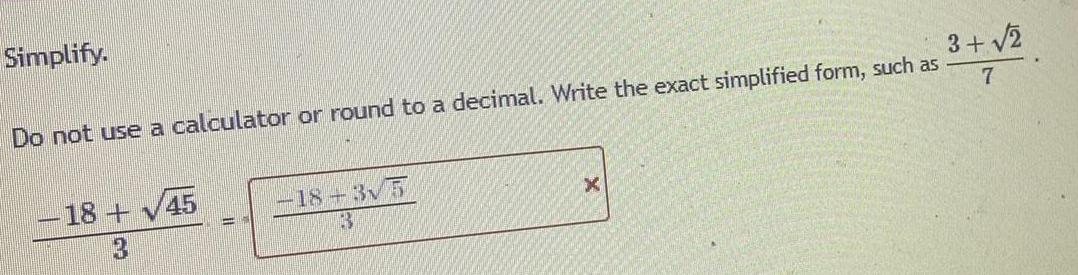
Basic MathSimplify.
Do not use a calculator or round to a decimal. Write the exact simplified form, such as 3+√2/7
18+ √45
-18-3√5
3
X
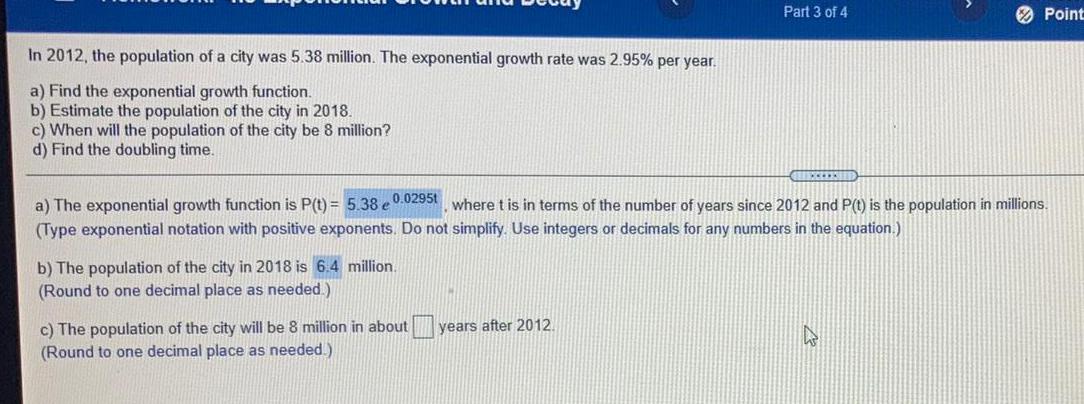
Math
Basic MathIn 2012, the population of a city was 5.38 million. The exponential growth rate was 2.95% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 8 million?
d) Find the doubling time.
b) The population of the city in 2018 is 6.4 million.
(Round to one decimal place as needed.)
CHURCZESNE
a) The exponential growth function is P(t) = 5.38 0.0295t, where t is in terms of the number of years since 2012 and P(t) is the population in millions.
(Type exponential notation with positive exponents. Do not simplify. Use integers or decimals for any numbers in the equation.)
c) The population of the city will be 8 million in about
(Round to one decimal place as needed.)
Part 3 of 4
years after 2012
Point

Math
Basic MathHeather participating in a 5-day cross
country biking challenge.she biked for
53,68,64, and 65 miles on the four days.
How many miles does she need to bike on
the last day so that her average (mean) is
59

Math
Basic MathA bass guitarist worked on 14 music projects last year. He wrote and produced 5 projects. He wrote a total of 8 projects. He produced a total of 11 projects. Use a Venn diagram to determine (a) how many projects he wrote but did not produce, and (b) how many projects he produced but did not write.
Complete the Venn diagram. Let W be the set of projects the bass guitarist wrote and P be the set of projects he produced.
![Solve for all solutions to the trigonometric equation 5 sin (θ/3-1) = -1/5 on the interval [-π, 5]. Find exact answers if possible, and enter your answer as a comma separated list.](https://media.kunduz.com/media/sug-question/raw/59051703-1657827197.9708471.jpeg?w=256)
Math
Basic MathSolve for all solutions to the trigonometric equation 5 sin (θ/3-1) = -1/5 on the interval [-π, 5]. Find exact answers if possible, and enter your answer as a comma separated list.

Math
Basic MathWhooping cough vaccine: Some parents fear that vaccinations may have adverse long-term effects on their children's health. In 2009 the Journal of the American Academy of Pediatrics published research on a routine childhood vaccine for whooping cough. The researchers studied 6811 children born between 1993 and 1997 in Leicestershire, UK. Parents answered questions over a 10+ year period about their children's respiratory symptoms. Researchers then linked this data to independently collected vaccination data from the National Health Service database. They divided the children into groups based on vaccine history (complete vaccines, partial vaccines, no vaccines) and compared respiratory symptoms. The study provided no evidence that vaccinated children were more likely to have respiratory problems such as wheeze and asthma.
Which question is this observational study designed to answer?
Are infants who are vaccinated against whooping cough more likely to develop wheezing disorders and asthma in later years?
Does vaccinating infants against whooping cough cause wheezing disorders or asthma in later years?
Are infants who receive a whooping cough vaccination less likely to develop whooping cough in later years?
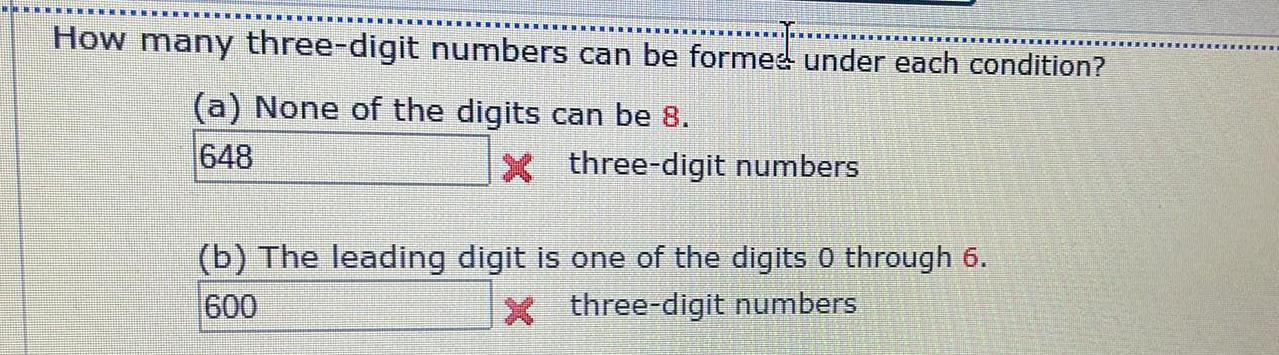
Math
Basic MathHow many three-digit numbers can be formed under each condition?
(a) None of the digits can be 8.
(b) The leading digit is one of the digits 0 through 6.

Math
Basic MathA car insurance company charges insurance premium in proportion to the car's value. For a $12,000 car, the monthly premium is $85. Laney pays a $120 monthly premium for her car. To the nearest dollar, how much is her car valued at?

Math
Basic MathConsider the expression √640, which simplifies to an expression in the form A√B. Simplify this
expression completely and place the appropriate numbers in the boxes given.

Math
Basic MathAt the gift shop, they sell small greeting cards and large greeting cards. The cost of a
small greeting card is $2.15 and the cost of a large greeting card is $5.40. How much
would it cost to get 2 small greeting cards and 5 large greeting cards? How much
would it cost to get a small greeting cards and y large greeting cards?
Total cost, 2 small greeting cards and 5 large greeting cards:
Total cost, a small greeting cards and y large greeting cards:
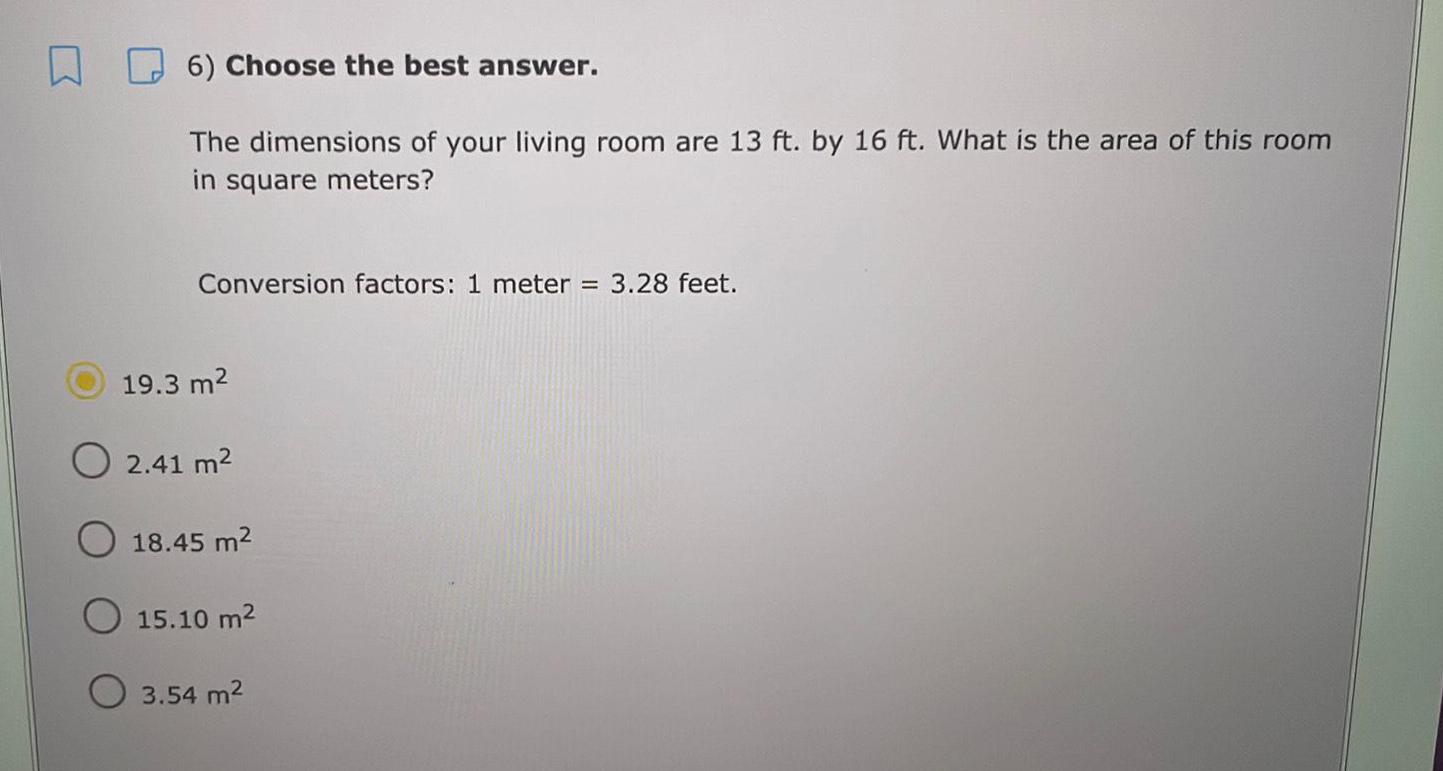
Math
Basic MathChoose the best answer.
The dimensions of your living room are 13 ft. by 16 ft. What is the area of this room in square meters?
Conversion factors: 1 meter = 3.28 feet.
19.3 m²
2.41 m2
18.45 m²
15.10 m²
3.54 m²
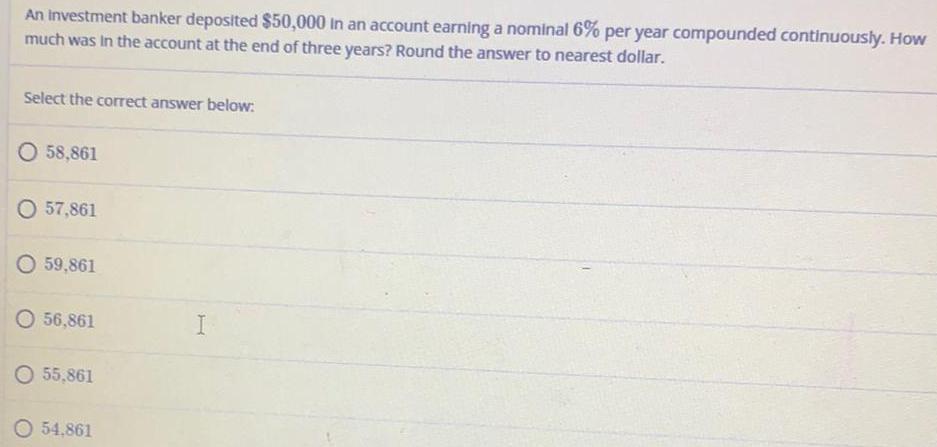
Math
Basic MathAn investment banker deposited $50,000 in an account earning a nominal 6% per year compounded continuously. How much was in the account at the end of three years? Round the answer to nearest dollar.
Select the correct answer below:
58,861
57,861
59,861
56,861
55,861
54,861
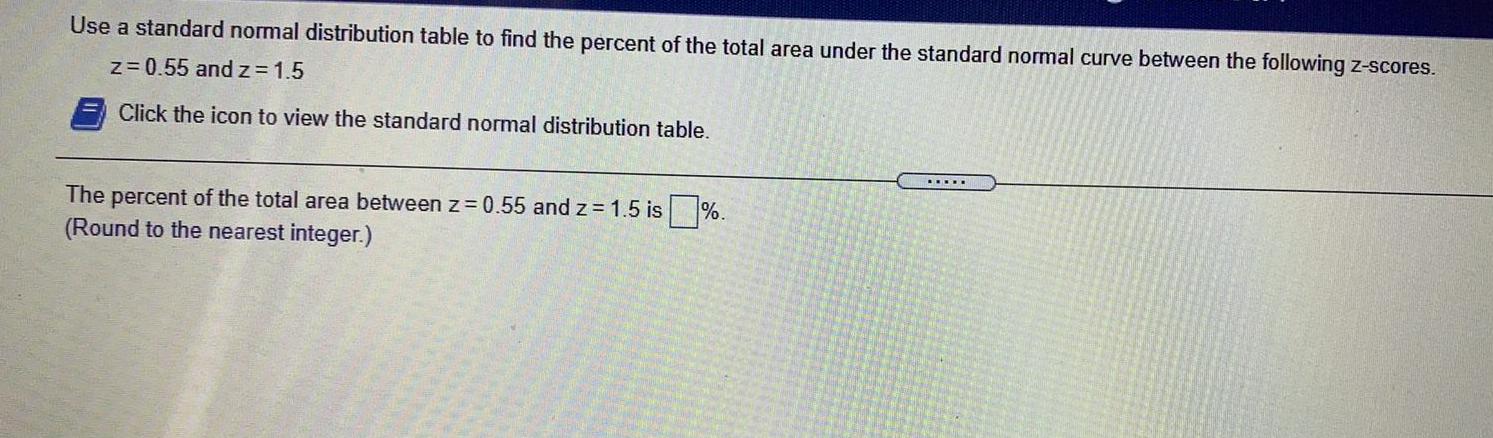
Math
Basic MathUse a standard normal distribution table to find the percent of the total area under the standard normal curve between the following z-scores.
z = 0.55 and z=1.5
Click the icon to view the standard normal distribution table.

Math
Basic MathIn an orchestra, 25 people can play stringed instruments, 21 can play brass, and 12 can play percussion. Further, 9 of the performers can play both strings and brass,
whereas 4 can play both strings and percussion. If no one can play all three types of instruments, what are the maximum and minimum numbers of people in the
orchestra? (Hint: Consider expressing the numbers in some of the regions of your diagram in terms of a single unknown, say x.)
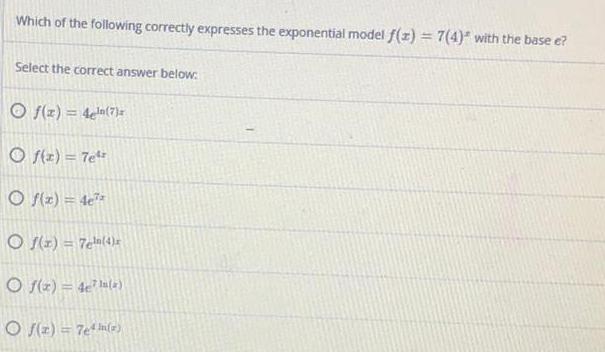
Math
Basic MathWhich of the following correctly expresses the exponential model f(x) = 7(4)x with the base e?
Select the correct answer below:
f(z)=4eln(7)
f(x) = 7e4x
f(x) = 4e7x
f(x) = 7eln(4)x
f(x) = 4e7ln(x)
f(z) = 7e4h(z)

Math
Basic MathA pool measuring 8 meters by 20 meters is surrounded by a path of uniform width, as shown in the figure. If the area of the pool and the path combined is 864 square meters, what is the width of the path?
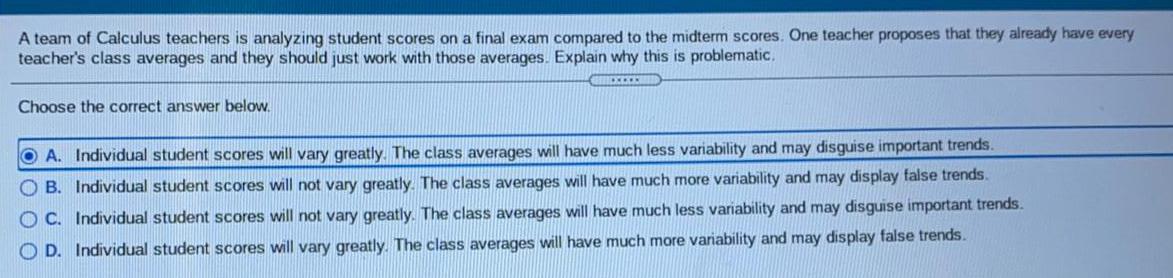
Math
Basic MathA team of Calculus teachers is analyzing student scores on a final exam compared to the midterm scores. One teacher proposes that they already have every
teacher's class averages and they should just work with those averages. Explain why this is problematic.
Choose the correct answer below.
A. Individual student scores will vary greatly. The class averages will have much less variability and may disguise important trends.
B. Individual student scores will not vary greatly. The class averages will have much more variability and may display false trends.
C. Individual student scores will not vary greatly. The class averages will have much less variability and may disguise important trends.
D. Individual student scores will vary greatly. The class averages will have much more variability and may display false trends.

Math
Basic MathNotice how the semicolons help the writer to separate different parts of a sentence that also includes commas.
Directions: Determine whether or not the following sentences are grammatically correct.
Sentence
Over the summer we ate pizza with cheese, pepperoni, and olives; hamburgers with bacon, ketchup, and mustard; and
barbecued ribs with potato salad, coleslaw, and fresh rolls.
I have always tried to be consistent; I never stop changing.
Many of the people who live here are seniors however; an underclassmen could get in by filing an application.
Correct Incorrect

Math
Basic MathEach course at Mt. Regis College is worth either 3 or 4 credits. The
members of the men's soccer team are taking a total of 48 courses that
are worth a total of 155 credits. How many 3-credit courses and how
many 4-credit courses are being taken?
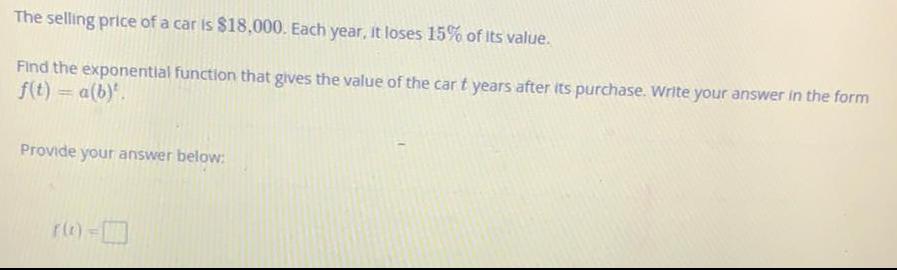
Math
Basic MathThe selling price of a car is $18,000. Each year, it loses 15% of its value.
Find the exponential function that gives the value of the car t years after its purchase. Write your answer in the form
f(t) = a(b)t
Provide your answer below:
Math
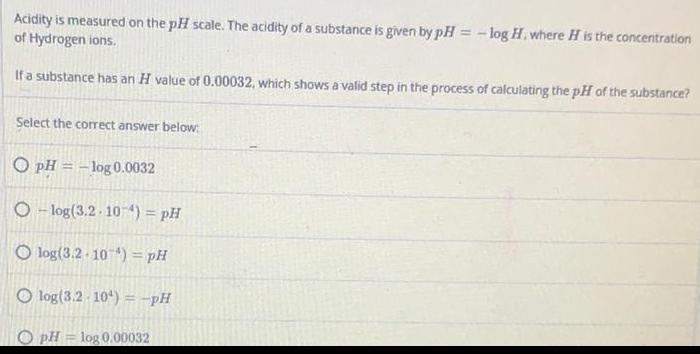
Basic MathAcidity is measured on the pH scale. The acidity of a substance is given by pH = -log H, where H is the concentration of Hydrogen ions.
If a substance has an H value of 0.00032, which shows a valid step in the process of calculating the pH of the substance?
Select the correct answer below:
pH = -log 0.0032
-log(3.2 10 4) = pH
log(3.2 10 ) = pH
log (3.2 10) = -pH
pH = log 0.00032

Math
Basic MathIn 2011 the U.S. Department of Transportation reported with 95% confidence that the average
length of a motor vehicle trip in the United States was 9.72 miles with a margin or error of 0.22
miles.
With 95% confidence the authors of the report are claiming that the true average length of a motor
vehicle trip in the United States is between
The level of confidence for this estimate is

Math
Basic MathAn accountant for a corporation forgot to pay the firm's income tax of $725,835.68 on time. The government charged a penalty of 8.4% interest for the 49 days the money was late. Find the total amount (tax and penalty) that was paid. Assume 365 days in a year

Math
Basic MathIf two lines are parallel, the alternate interior angles are congruent. Choose the equivalent statement.
A. If alternate interior angles are congruent, the lines are parallel.
B. If alternate interior angles are not congruent, then the lines are not parallel.
C. If two lines are not parallel, then alternate interior angles are not congruent.

Math
Basic MathWhich of the following statements is not a true statement?
A. The legs of a triangle are the sides adjacent to the right angle.
B. The hypotenuse is directly across from the right angle.
C. The Pythagorean theorem can only be used with right triangles.
D. The hypotenuse is always the shortest side length.

Math
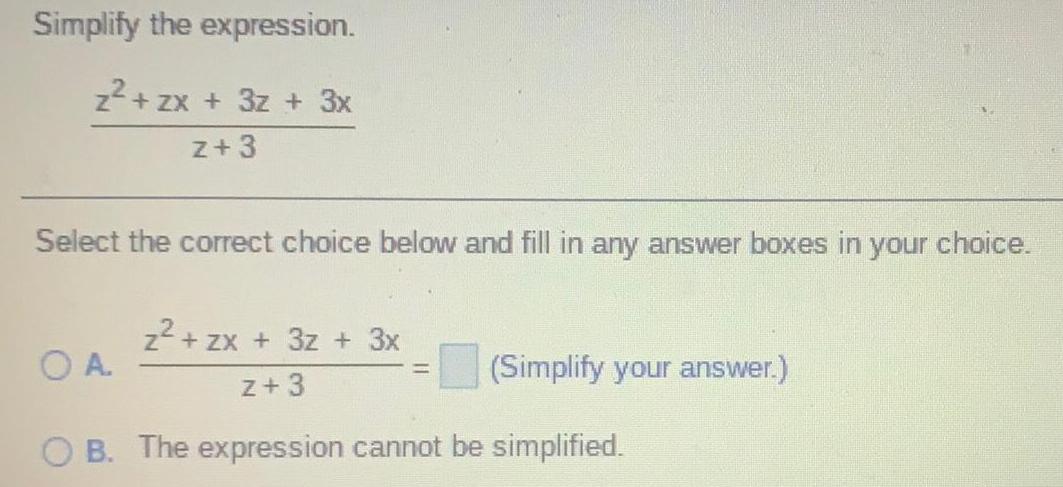
Basic MathBarbara picked 36 apples. She needs to put of the apples in a basket. Barbara says she will put 12 apples in the basket. Is Barbara correct? Explain.

Math
Basic MathA certain virus infects one in every 400 people. A test used to detect the virus in a person is positive 85% of the time if the person has the virus and 8% of the time if the person does not have the virus. (This 8% result is called a false positive.) Let A be the event "the person is infected" and B be the event "the person tests positive".
a) Find the probability that a person has the virus given that they have tested positive, i.e. find P(A/B). Round your answer to the nearest tenth of a percent and do not include a percent sign.
b) Find the probability that a person does not have the virus given that they test negative, i.e. find P(A' | B'). Round your answer to the nearest tenth of a percent and do not include a percent sign.

Math
Basic MathThe Foster family and the Robinson family each used their sprinklers last summer. The water output rate for the Foster family's sprinkler was 25 L per hour. The water output rate for the Robinson family's sprinkler was 40 L per hour. The families used their sprinklers for a combined total of 50 hours, resulting in a total water output of 1475 L. How long was each sprinkler used?

Math
Basic MathA tinsmith wants to make a small windowsill planter from a 60 cm x 18 cm sheet of copper. She'll form it by cutting equally sized squares from each of the four corners of the sheet, folding up the resulting flaps to form the sides of the planter, and then soldering the four vertical edges. If she wants the ratio of the planter's width to height to be 7, what will be the ratio of its length to width? Write the exact answer. Do not round.

Math
Basic MathKarla invests $10,000 into an account with a 2.2% interest that is compounded annually.
How much money will she have in this account if she keeps it for 5 years? Round your answer to the nearest dollar. Do not round at any other point in the solving process; only round your answer.
Provide your answer below:
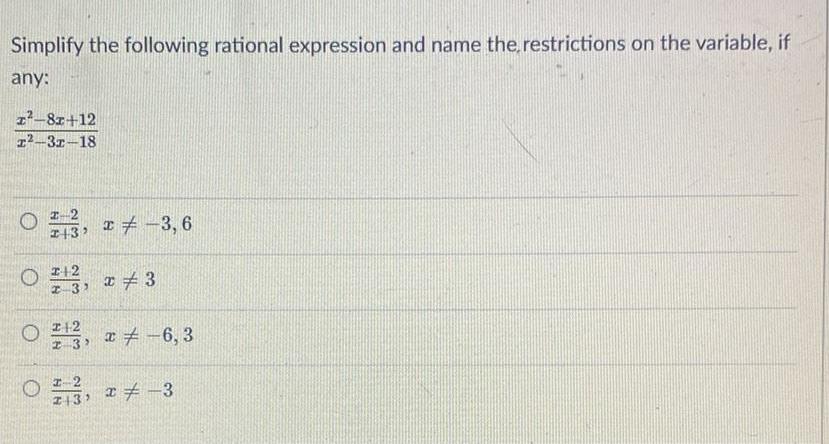
Math
Basic MathSimplify the following rational expression and name the restrictions on the variable, if any: x^2 - 8x + 12 / x^2 - 3x - 18
x-2/x+3, x ≠ 3, 6
x+2/x-3, x ≠ 3
x+2/x-3, x ≠ -6, 3
x-2/x+3, x ≠ -3