Basic Math Questions and Answers

Math
Basic MathWorking together, two pumps can drain a certain pool in 6 hours. If it takes the older pump 15 hours to drain the pool by itself, how long will it take the newer pump to drain the pool on its own?
Do not do any rounding.

Math
Basic MathA voltage V across a resistance R generates a current
I=V/R. If a constant voltage of 6 volts is put across a
resistance that is increasing at a rate of 0.2 ohms per
second when the resistance is 4 ohms, at what rate is the
current changing? (Give units.)
rate =
![Find two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid. Express each coordinate as an
integer or simplified fraction, or round to four decimal places as necessary.](https://media.kunduz.com/media/sug-question/raw/57731034-1657658109.4684806.jpeg?w=256)
Math
Basic MathFind two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid. Express each coordinate as an
integer or simplified fraction, or round to four decimal places as necessary.


Math
Basic MathA population numbers 18,000 organisms initially and grows by 15.2% each year.
Suppose Prepresents population, and t the number of years of growth. An exponential model for
the population can be written in the form P = abt where
P=
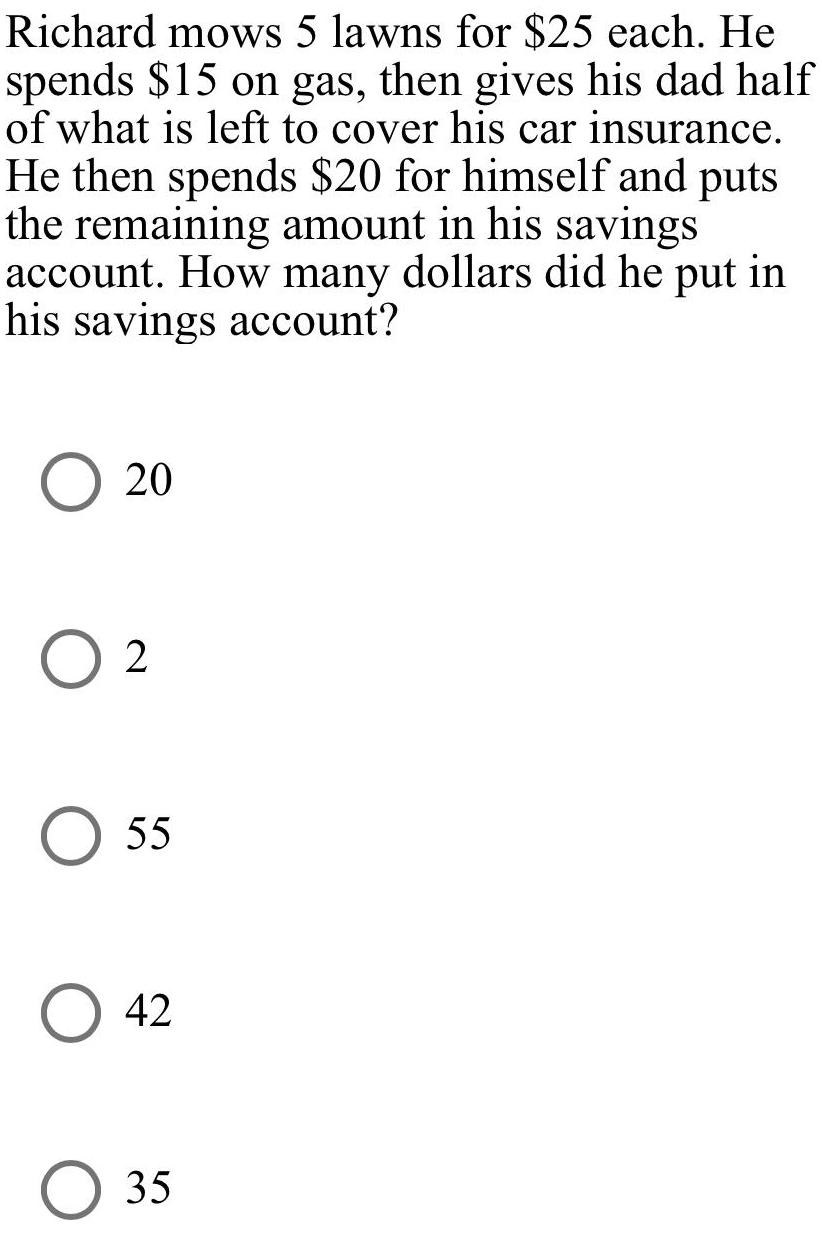
Math
Basic MathRichard mows 5 lawns for $25 each. He
spends $15 on gas, then gives his dad half
of what is left to cover his car insurance.
He then spends $20 for himself and puts
the remaining amount in his savings
account. How many dollars did he put in
his savings account?
20
2
55
42
35

Math
Basic MathIf a person's eye level is h meters above sea level and she can see d kilometers to the horizon, then d = 3.57√h. Suppose the person's eye level is 8.41 meters above sea level. How far can she see to the horizon?
Round your answer to the nearest tenth.


Math
Basic MathThe police department in your city was asked by the
mayor's office to estimate the cost of crime. The
police began their study with burglary records, taking
a random sample of 500 files since there were too
many crime records to calculate statistics for all of the
crimes committed. If the average dollar loss in a
burglary, for this sample size 500 is $678, with a
standard deviation of $560, construct the 95%
confidence interval for the true average dollar loss in
burglaries rounded to the nearest dollar amount. We
can be 95% confident that the upper limit of our
interval of dollar loss in crimes committed is

Math
Basic MathIf 7000 dollars is invested in a bank account at an interest rate of 7 per cent per year,
Find the amount in the bank after 5 years if interest is compounded annually:
Find the amount in the bank after 5 years if interest is compounded quarterly:
Find the amount in the bank after 5 years if interest is compounded monthly.
Finally, find the amount in the bank after 5 years if interest is compounded continuously.

Math
Basic MathSuppose that a population begins at a size of 100 and grows continuously at a rate of
200% per year. Give the formula for calculating the size of that population after t
years.
A) A = 100 + te²
B) A = 100+ e²t
C) A = 100e²t
D) A = 100+ 2et
Math
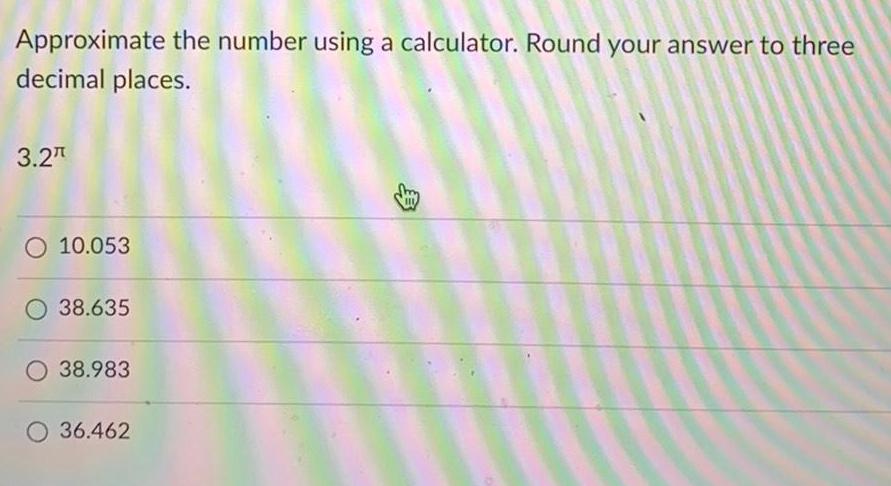
Basic MathApproximate the number using a calculator. Round your answer to three
decimal places.
3.2π
10.053
38.635
38.983
36.462

Math
Basic MathDecide whether a line with the given slope slants upward or downward or is horizontal or vertical
m=3/2
Choose the correct answer below
A horizontal
B. upward
C. downward
D. vertical

Math
Basic MathA building contractor is building a backyard playground and wishes to put down rubber mulch to provide safety from falls. The contractor wishes to put the mulch in a pit in the shape of a rectangular solid 23 feet long, 17 feet wide, and 9 inches deep.
a) Determine the volume, in cubic feet, of mulch the contractor will need. When appropriate, use the key on your calculator.
b) If mulch costs $9 per cubic foot, what will the cost of mulch be?
a) The volume is ft³.
(Type an integer or decimal.)
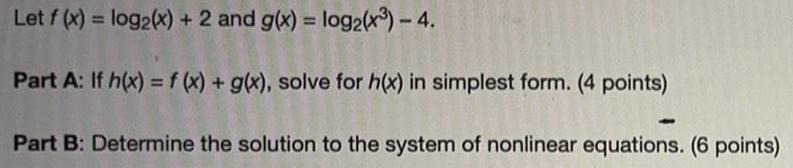
Math
Basic MathLet f (x) = log2 (x) + 2 and g(x) = log2 (x³) - 4.
Part A: If h(x) = f (x) + g(x), solve for h(x) in simplest form. (4 points)
Part B: Determine the solution to the system of nonlinear equations. (6 points)

Math
Basic MathCarl owns a company that washes the windows of office buildings. He recently
signed a contract for a large office building and estimates that it would take 2 days
for 4 workers to wash the windows. Write an equation to describe the relationship
between time (t) and the number of workers (n), which are inversely
proportional.
A) t = 2/n
B) t = 6/n
C) t = 16/n
D) t = 8/n

Math
Basic MathThe operations manager of a large production plant would like to estimate the average amount of time workers take to assemble a new electronic component. After observing a number of workers assembling similar devices, she guesses that the standard deviation is 7 minutes. How large a sample of workers should she take if she wishes to estimate the mean assembly time to within 20 seconds. Assume the confidence level to be 99%.
Sample Size =

Math
Basic MathA population of bacteria triples every hour. Is this situation linear or exponential?
A) Linear, because the function increases
B) Linear, because the function increases by a common difference
C) Exponential, because the function decreases
D) Exponential, because the function grows by a common ratio

Math
Basic MathA station wagon covered a total distance of 3343 kilometres averaging a speed of
32 km/h in slow-moving traffic and 79 km/h in fast-moving traffic. The journey
took 56 hours. How many hours did the station wagon spend in slow-moving
traffic? (Hint distance = speed x time)

Math
Basic MathBeth can travel 203 miles in the same length of time it takes Anna to travel 192 miles. If Beth's
speed is 4 mph greater than Anna's, find both rates.
Hint: You'll be using the d = r*t formula, but in a different form. For the time column in the
table below, you should put in expressions using the formula t= d/r
a.Write down the unknown(s) you're being asked to find and assign a variable or expression
to represent it (them).
b. Organize the information provided in the table below.
Rate Time Distance
Beth
Anna
c.Using the information given in the problem and your table, write an equation representing
this scenario. Then solve the equation.
d. Write a sentence answering the question asked in the exercise using the appropriate units
of measure.
e.Assess your solution. Write a sentence indicating whether your solution makes sense. If it
doesn't make sense, explain why.

Math
Basic Mathtoy company recently added some made-to-scale models of racecars to their product line. The length of a certain racecar is 19 ft. Its width is 7 ft. The width of the e-cast replica is 1.75 in. Find the length of the model.

Math
Basic MathUse a graphing device to solve the inequality, as in Example 5. Express your answer using interval notation, with the endpoints of the intervals rounded to two decimals.
x3-8x2 - 11x + 18 ≥ 0

Math
Basic MathSuppose you have 60 kg of a radioactive material that decays 50% of its mass every
year. How much material will you have left after 4 years?
8.12 kg
32.1 kg
12.14 kg
3.14 kg

Math
Basic MathSuppose that you begin with 10 grams of magic crystals, and your crystals grow at a
continuous rate of 25% every day (that's why they're magic). How many grams of
crystals will you have after one week (7 days)?
85.28 g
47.68 g
100 g
57.55 g

Math
Basic MathAccording to a country's census, the number of people (in thousands) who are expected to be over 100 years old in year x is approximated by the function
f(x)=0.27x² +3.54x+50.78, where x = 0 corresponds to the year 2000 and the formula is valid through 2045.
(a) Find a formula giving the rate of change in the number of people over 100 years old.
(b) What is the rate of change in the number of people expected to be over 100 years old in the year 2015?
(c) Is the number of people expected to be over 100 years old increasing or decreasing in 2015?
(a) The formula for the rate of change of the number of people over the age of 100 is f'(x) =
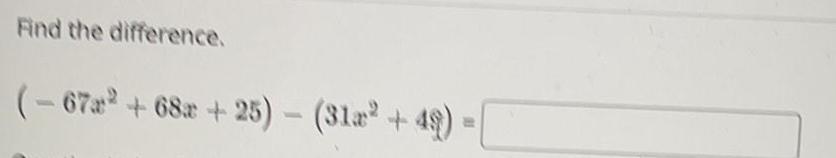
Math
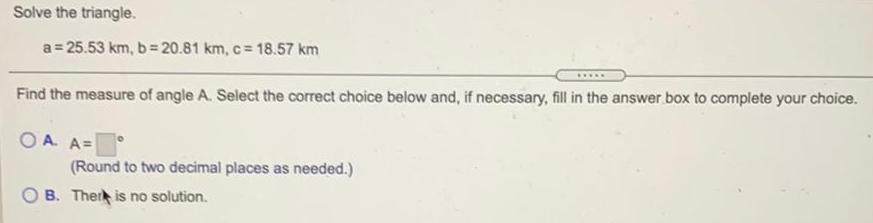
Basic MathSolve the triangle.
a=25.53 km, b=20.81 km, c= 18.57 km
Find the measure of angle A. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. A=
(Round to two decimal places as needed.)
B. There is no solution.

Math
Basic MathDivide the following and express your answer in appropriate scientific notation:
6.84 x 10(71)/1.2 × 10(43)
Math
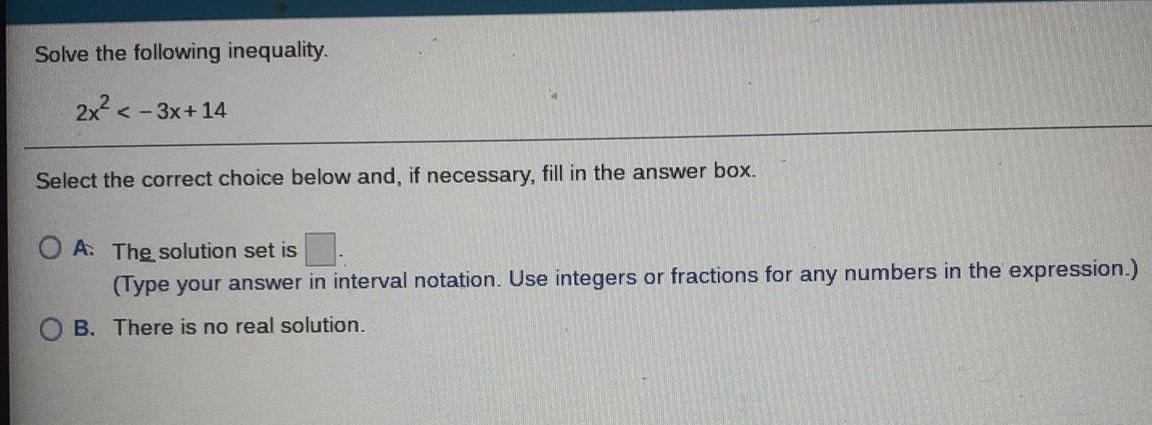
Basic MathSolve the following inequality.
2x² <-3x+14
Select the correct choice below and, if necessary, fill in the answer box.
A. The solution set is
(Type your answer in interval notation. Use integers or fractions for any numbers in the expression.)
B. There is no real solution.

Math
Basic MathA certain car model was expected to get 459 miles (highway) on 24 gallons of gas. What was the mean number of miles per gallon (mpg)?
The mean number of miles per gallon (mpg) is
(Round to the nearest tenth as needed.)

Math
Basic MathYou want to start saving up for a trip to Europe after you graduate from CSM in two
years. Your goal is to save $3000, so you decide to start a savings account that earns
2.5% interest compounded quarterly. How much should you deposit each quarter to
meet your goal?
$233.38
$600.00
$366.87
$122.03
Math
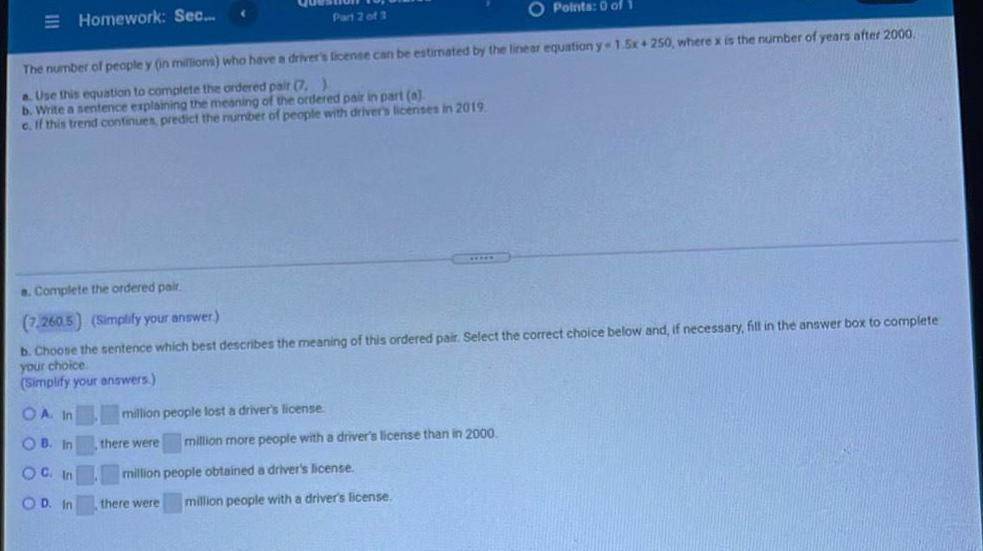
Basic MathThe number of people y (in millions) who have a driver's license can be estimated by the linear equation y-1.5x+250, where x is the number of years after 2000.
a. Use this equation to complete the ordered pair (7.)
b. Write a sentence explaining the meaning of the ordered pair in part (a).
c. If this trend continues, predict the number of people with driver's licenses in 2019.
Part 2 of 3
a. Complete the ordered pair. (Simplify your answer.)
b. Choose the sentence which best describes the meaning of this ordered pair. Select the correct choice below and, if necessary, fill in the answer box to complete
your choice
(Simplify your answers.)
A. In million people lost a driver's license.
B. In there were million more people with a driver's license than in 2000.
C. In million people obtained a driver's license.
D. In there were million people with a driver's license.

Math
Basic MathA restaurant manager has developed time guidelines for his kitchen staff. One such guideline requires a food prep worker to prepare 27 containers of granola in 7 minutes 40 seconds or less. What is the maximum time allowed per container?
![f(x) = -3/x^2
Find two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid. Express each coordinate as an Integer or simplified fraction, or round to four decimal places as necessary.](https://media.kunduz.com/media/sug-question/raw/57641901-1657655005.7401364.jpeg?w=256)
Math
Basic Mathf(x) = -3/x^2
Find two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid. Express each coordinate as an Integer or simplified fraction, or round to four decimal places as necessary.
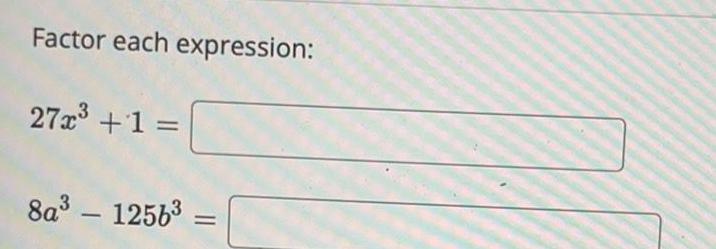

Math
Basic MathIn a circle with a radius of 6 ft, an arc is intercepted by a central angle of 3π/2 radians
What is the length of the arc?
2π ft
3π ft
6 π ft
9π ft

Math
Basic MathGiven the two functions, which statement is true?
f(x) = log15 x, g(x) = log15 (x+4)
g(x) is stretched vertically by a factor of 2 and shifted to the left 4 units
compared to f(x).
g(x) is shrunk vertically by a factor of 12 and shifted to the left 4 units compared
to f(x).
g(x) is stretched vertically by a factor of 2 and shifted to the right 4 units
compared to f(x).
g(x) is shrunk vertically by a factor of 12 and shifted to the right 4 units compared
to f(x).
![Which of the following polynomials is guaranteed by the Intermediate Value Theorem to have a zero on the interval [3, 4]?
Select the correct answer below:
f(x) = 2x² + x − 3
g(x) = -4x² + 3x - 4
h(x) = x³ - 2x² - x +4
j(x) = 2x² - 5x -5](https://media.kunduz.com/media/sug-question/raw/57856436-1657654865.0171726.jpeg?w=256)
Math
Basic MathWhich of the following polynomials is guaranteed by the Intermediate Value Theorem to have a zero on the interval [3, 4]?
Select the correct answer below:
f(x) = 2x² + x − 3
g(x) = -4x² + 3x - 4
h(x) = x³ - 2x² - x +4
j(x) = 2x² - 5x -5

Math
Basic MathAccording to a researcher's data, about 63% of all of San Diego has taken at least 1 dance class. Suppose that we obtain 300 randomly selected San Diegans.
a) Is the sample large enough to use the normal approximation for the binomial? Show it using the conditions.
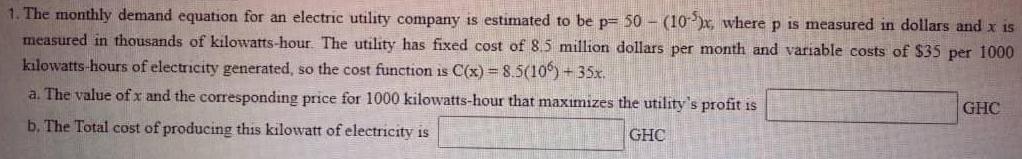
Math
Basic MathThe monthly demand equation for an electric utility company is estimated to be p= 50- (10)x, where p is measured in dollars and x is measured in thousands of kilowatts-hour. The utility has fixed cost of 8.5 million dollars per month and variable costs of $35 per 1000
kilowatts-hours of electricity generated, so the cost function is C(x) = 8.5(106) + 35x.
a. The value of x and the corresponding price for 1000 kilowatts-hour that maximizes the utility's profit is GHC
b. The Total cost of producing this kilowatt of electricity is GHC

Math
Basic MathThe hole for a footing needs to be 7 ft deep. If it is currently 1 ft 7 in. deep, how much deeper does it need to be dug? Give the answer in inches. The hole needs to be dug inches deeper.

Math
Basic MathLacey is at her house, which is located at (2, 4) on a coordinate grid. She wants to go to a bookstore that is located at (1, 6).
Which route could she take? Assume 1 unit = 1 mile.
A.1 mile to the right and 6 miles up
B.2 miles to the left and 1 mile up
C. 6 miles to the right and 1 mile up
D.1 mile to the left and 2 miles up

Math
Basic MathPsychologists use the formula i = 100m/c to measure a person's intelligence. Called the intelligence quotient, or I.Q., i is expressed in terms of m, the person's mental age, and c, his or her chronological age, or number of years he or she has lived.
a) Find the I.Q. of someone whose mental age is 18 and whose chronological age is 15.
b) Solve the formula for m in terms of i and c.
c) Check your answer for part a of this exercise in your formula for part b, letting m= 18 and c = 15.
d) Solve the formula that you wrote for part b of this exercise for c in terms of i and m.

Math
Basic MathThe average number of pounds of red meat a person consumes each year is 196 with a standard deviation of 22 pounds (Source: American Dietetic Association). If a sample of 50 individuals is randomly selected, find the probability that the mean of the sample will be greater than 200 pounds.
A 0,7613
B. 0.8815
C 0.0985
D. 0.9015

Math
Basic MathThe perimeter of a square box is 12x + 32. Drag numbers to complete an equivalent expression that shows the perimeter as four times the side length of the box. Numbers may be used once, more than once, or not at all.
1 2 3 4 5 6 7 8

Math
Basic MathIdentify the explicit formula for the sequence given by the following recursive
formula:
f(n)=
[ƒ(1)=-2
f(n)=f(n-1)+4 if n>1
A) f(n) = 2 - 4(n − 1)
B) f(n) = −4 + 2(n − 1)
C) f(n) = -2 + 4(n − 1)
D) f(n) = 4 - 2(n − 1)

Math
Basic MathGiven the function f(x) = 2x - 1, evaluate and simplify the expressions below. See special
instructions on how to enter your answers.
f(a) =
f(a+h) =
f(a+h)-f(a)/h =
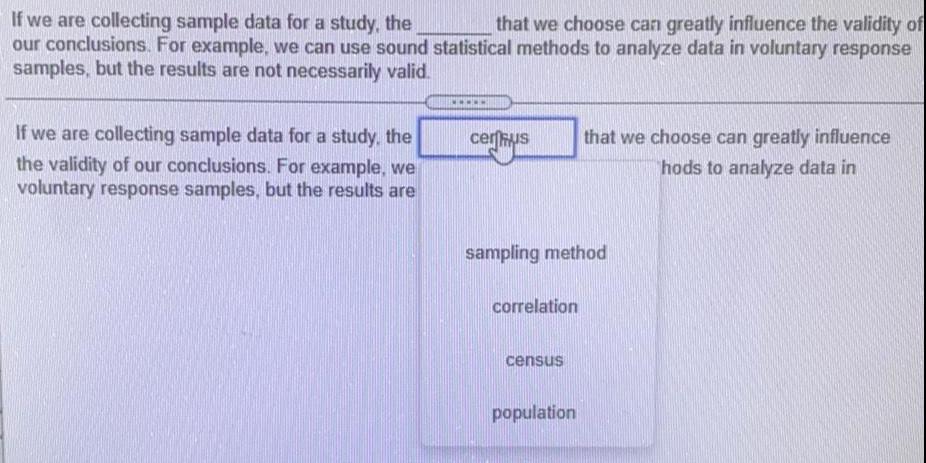
Math
Basic MathIf we are collecting sample data for a study, the that we choose can greatly influence the validity of our conclusions. For example, we can use sound statistical methods to analyze data in voluntary response samples, but the results are not necessarily valid. If we are collecting sample data for a study, the the validity of our conclusions. For example, we voluntary response samples, but the results are

Math
Basic MathA line passes through the point (, 2) and has a slope of -2.
Write an equation in point-slope form for this line.