Basic Math Questions and Answers

Math
Basic MathRhett decides to build a square room for his movie and music collection. If the area of the room is 4x² + 28x + 49 square feet, what is the length of one side of the room?
(7x + 2) feet
(2x + 7) feet
(2x-7) feet
(7x-2) feet
Math
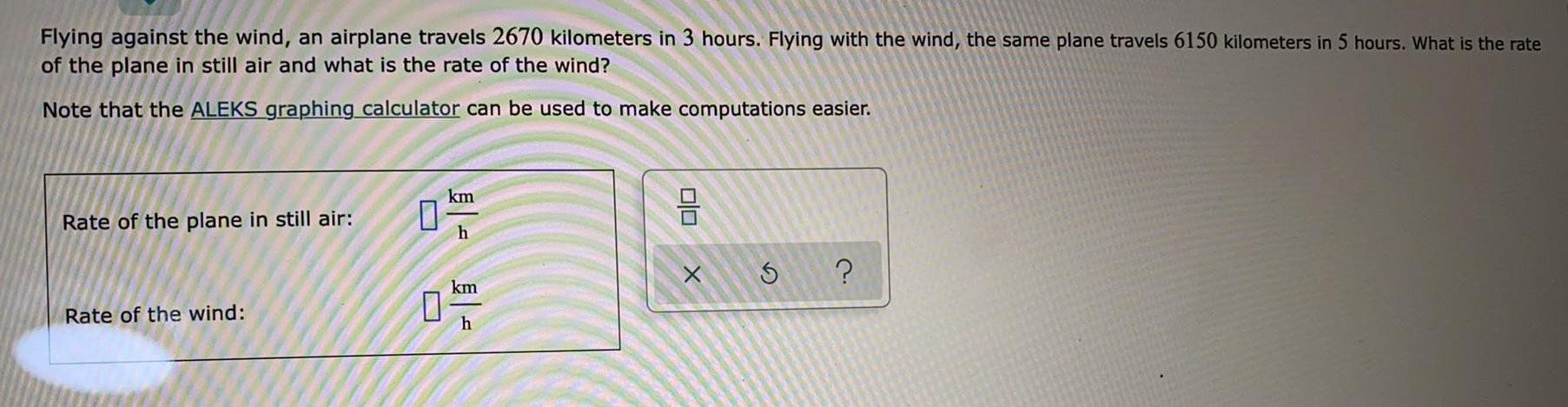
Basic MathFlying against the wind, an airplane travels 2670 kilometers in 3 hours. Flying with the wind, the same plane travels 6150 kilometers in 5 hours. What is the rate of the plane in still air and what is the rate of the wind?
Note that the ALEKS graphing calculator can be used to make computations easier.
Math
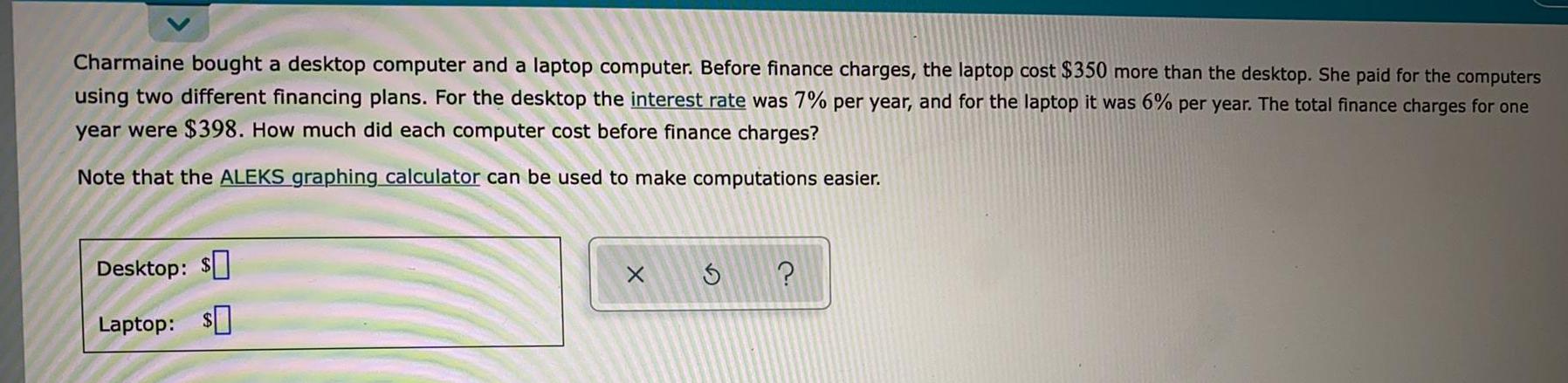
Basic MathCharmaine bought a desktop computer and a laptop computer. Before finance charges, the laptop cost $350 more than the desktop. She paid for the computers using two different financing plans. For the desktop the interest rate was 7% per year, and for the laptop it was 6% per year. The total finance charges for one year were $398. How much did each computer cost before finance charges? Note that the ALEKS graphing calculator can be used to make computations easier.
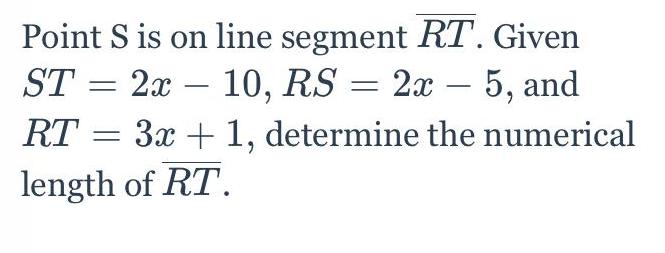
Math
Basic MathPoint S is on line segment RT. Given ST= 2x- 10, RS = 2x - 5, and RT = 3x + 1, determine the numerical length of RT.

Math
Basic MathCertain radioactive material decays in such a way that the mass remaining after t years is given by the function
m(t) = 275e-0.045
where m(t) is measured in grams.
(a) Find the mass at time t = 0.
Your answer is
(b) How much of the mass remains after 10 years?
Your answer is

Math
Basic MathFind the circumference and area of a circle with a diameter of 22 inches. Leave your answers in terms of pl.

Math
Basic MathA wheel with three numbers on it--0, 1, and 2--is spun so that there is a 40% chance that the wheel lands on zero, a 10% chance the wheel lands on one, and a 50% chance the wheel lands on two. You get back the amount in dollars of the number that the wheel lands on. If it costs $1 to
play, what is the expected value of the game? *
-$1.10
-$0.10
$0.10
$0.20
$1.10
Math
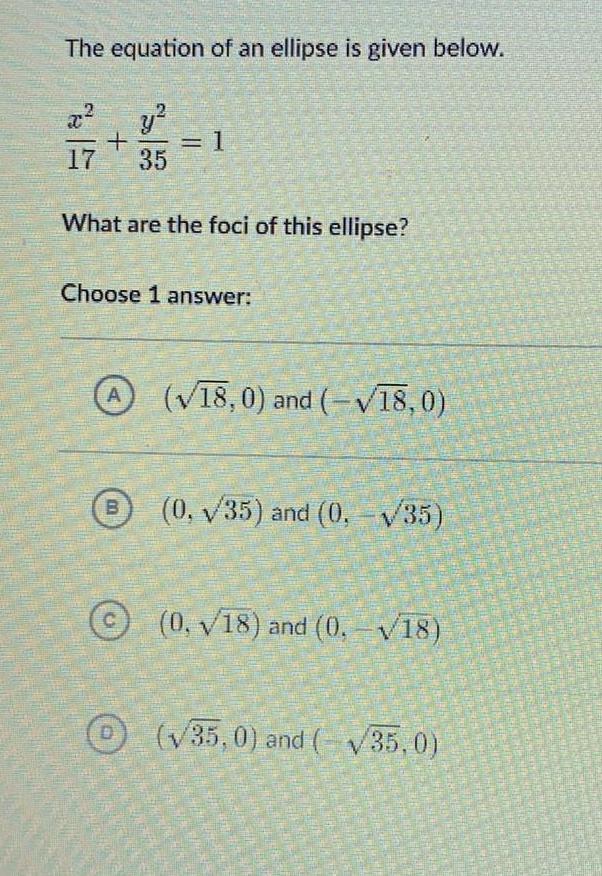
Basic MathThe equation of an ellipse is given below.
x2/17+y²/35= 1
What are the foci of this ellipse?
Choose 1 answer:
A(√18,0) and (-√18,0)
B (0, √35) and (0, -√/35)
c (0, 18) and (0, -√18)
D (√35,0) and (-√35,0)

Math
Basic MathA company makes electronic gadgets. One out of every 50 gadgets is faulty, but the company doesn't know which ones are faulty until a buyer complains. Suppose the company makes a $3 profit on the sale of any working gadget, but suffers a loss of $80 for every faulty gadget because they have to repair the unit. Can the company expect a profit in the long term? *
Yes, they can expect a profit.
No, they will lose money in the long term.


Math
Basic MathYou rent an apartment that costs $1500 per month during the first year, but the rent is set to go up 11.5% per year. Write a recursive formula to show what the rent is during the nth year of living in the apartment.

Math
Basic MathWhich property should be used next in this solution process?
3x +2+3= 7 (x - 1)-4
3x+5= 7 (x-1) - 4
A Commutative Property of Addition
B. Identity Property of Multiplication
C. Associative Property of Multiplication
D. Distributive Property

Math
Basic MathA company manufactures computers. Function represents the number of components that a new employee can assemble per day. Function E represents the number of components that an experienced employee can assemble per day. In both functions, t represents the number of hours worked in one day.
N(t) = 50t/t + 4
E(t) = 70t/t + 3
Which function describes the difference of the number of components assembled per day by the experienced and new employees?

Math
Basic MathFind the volume of a cylinder with a diameter of 8 inches and a height that is three times the radius. Use 3.14 for pl and round your answer to the nearest hundredth. (Hint: You may only enter numerals, decimal points, and negative signs in the answer blank)

Math
Basic MathSuppose the points from a class total 1000 points and are divided into 600 points on the Exams and 400 points on Homeworks. If you averaged 75% on the exams and 90% on the homeworks, what is your overall percentage? Try to answer this with rate and mixture equation that we have used in many contexts.

Math
Basic MathIdentify whether the following equation represents an exponential function.
g(x) = -22.85x - 50.75
NOT an exponential function
exponential function
Math
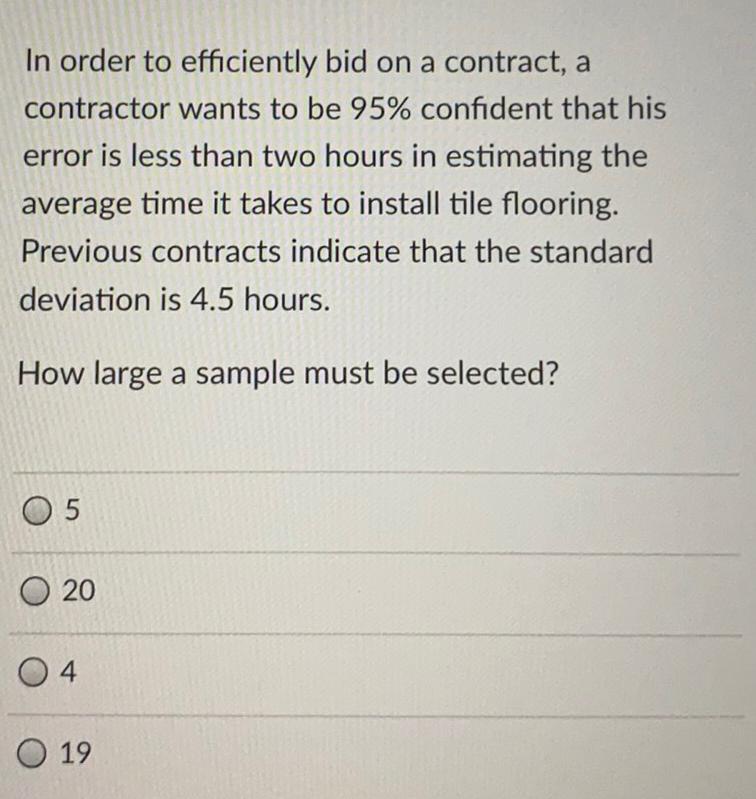
Basic MathIn order to efficiently bid on a contract, a contractor wants to be 95% confident that his error is less than two hours in estimating the average time it takes to install tile flooring. Previous contracts indicate that the standard deviation is 4.5 hours.
How large a sample must be selected?
5
20
4
19
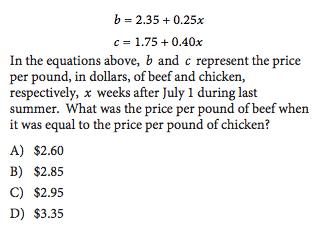
Math
Basic Mathb = 2.35 +0.25x
c = 1.75 +0.40x
In the equations above, b and c represent the price per pound, in dollars, of beef and chicken, respectively, x weeks after July 1 during last summer. What was the price per pound of beef when it was equal to the price per pound of chicken?
A) $2.60
B) $2.85
C) $2.95
D) $3.35

Math
Basic MathLook at an example of a polynomial 7x³ - 2x²+x-5, we say that the degree of this polynomial is 3, which is the highest power.
For this week's discussion, briefly explain how the degree of a divider is compared to the degree of the remainder. Divide the following expression, and compare the degree of the divider:
x+3 and the degree of the remainder: (7x3-2x²+x-5)/x + 3
Math
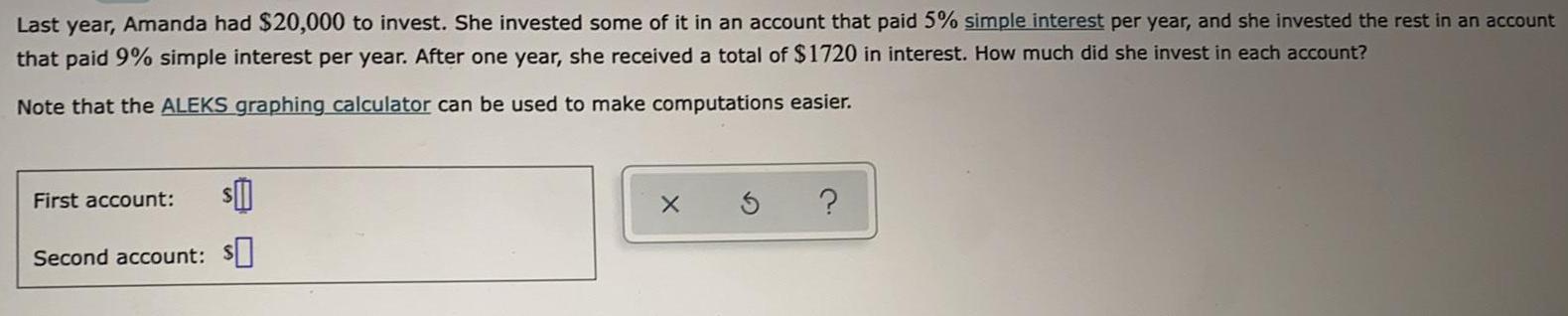
Basic MathLast year, Amanda had $20,000 to invest. She invested some of it in an account that paid 5% simple interest per year, and she invested the rest in an account that paid 9% simple interest per year. After one year, she received a total of $1720 in interest. How much did she invest in each account?
Note that the ALEKS graphing calculator can be used to make computations easier.
First account: $
Second account: $

Math
Basic MathP(q) = -0.01(q-250) (q - 80)
The equation above gives the profit, P(q), in dollars, earned by a cupcake bakery when q
cupcakes are produced. What is the best interpretation of the number 80 in this context?
A 80 is a number of cupcakes for which the profit is equal to $0.
B 80 is the number of cupcakes that corresponds to the maximum profit.
C 80 is the number of cupcakes that corresponds to the minimum profit.
D $80 is the maximum profit, in dollars.

Math
Basic MathYou want to create a custom border for a picture of you and your family. The picture measures 8 inches by 10 inches. What should the width of the
picture frame be if the final area, including the picture, is three times the area of the picture by itself?
• Write answer as a number only.
Round answer to two decimal places in needed.
Math
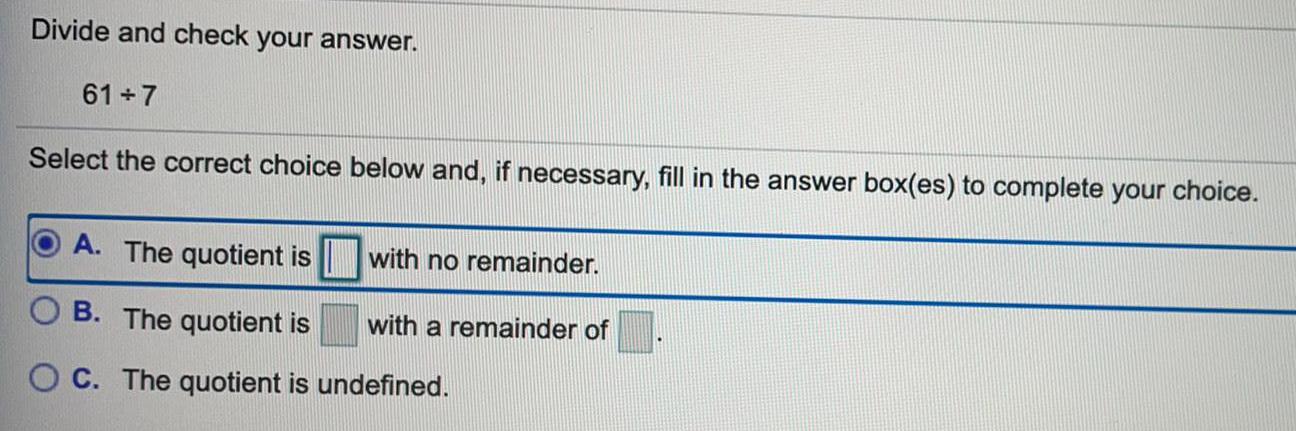
Basic MathDivide and check your answer.
61+7
Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
A. The quotient is
with no remainder.
B. The quotient is with a remainder of
OC. The quotient is undefined.

Math
Basic MathRicardo transformed the quadratic parent function f(x) to create g(x). After the transformation, he noticed that the domain and range were the same for f(x) and g(x). Which of the following could NOT represent g(x)?

Math
Basic Math4. (Like 2003 Exit) Myesha makes hand-painted pots. Her overhead costs are $650 per week, and she pays an additional $12 per pot in material costs. What will be her total expenses if she sells 50 pots this week.
A $250
B $650
C $1250
D $1650

Math
Basic MathYou pick a card from a deck. If you get a face card (J,Q,K), you win $5. If you get an ace, you win $30 plus an extra $60 for the ace of hearts. For any other card you win nothing. Find the expected value you will win. *

Math
Basic MathJustin opened a savings account with $900 that pays no interest. He deposits an additional $190 each week thereafter. How much money would Justin have in the account 30 weeks after opening the account?

Math
Basic MathDakota wants cover his patio with concrete pavers. If the patio is shaped like a trapezoid whose bases are 16 feet and 18 feet and whose height is 14 feet, how many square feet of pavers will he need?

Math
Basic Math2. A student bought a pair of sunglasses in the USA and paid $35.50. In England, an
identical pair of sunglasses costs £26.99. The exchange rate is £1 = $1.42. In which
country were the sunglasses cheaper, and by how much?
Math
Basic MathOscar's dog house is shaped like a tent. The slanted sides are both 5 feet
long and the bottom of the house is 6 feet across. What is the height of his
dog house, in feet, at its tallest point?
4 feet
3 feet
5 feet
6 feet

Math
Basic Math7) It takes a hose 5 minutes to fill a rectangular aquarium 9 inches long, 10 inches wide, and 13
inches tall. How long will it take the same hose to fill an aquarium measuring 1.5 feet by 2 feet by
2.5 feet?

Math
Basic MathA survey of 2450 golfers showed that 281 of them are left-handed. Use this data to construct a 98% confidence interval for the proportion of golfers that are left- handed.
(0.369, 0.451)
(0.203, 0.293)
(0.100, 0.130)
(0.683, 0.712)

Math
Basic MathA random sample of 40 students has a mean annual earnings of $3120 and a population standard deviation of $677. Use this sample data to construct a 95% confidence interval for the population mean, μ, of all student earnings.
($2910, $3330)
($1987, $2346)
($4812, $5342)
($210, $110)

Math
Basic MathAn object is dropped from a tower, 166 ft above the ground. The object's height above ground t sec into the fall is s=166-16t²
a. What is the object's velocity, speed, and acceleration at time t?
b. About how long does it take the object to hit the ground?
c. What is the object's velocity at the moment of impact?
The object's velocity at time t is

Math
Basic MathA class has 35 students. In how many different ways can six students form a group for an activity?
(Assume the order of the students is not important.)
There are different ways that the six students can form a group for an activity.
(Type a whole number.)

Math
Basic MathThe expression is given in standard form. Rewrite it in factored form. If it cannot be rewritten in factored form, write "cannot be done."
p² + 18p-40
a (p-20)(p+2)
b (p+20)(p+2)
c (p+20)(p-2)
d (p-20)(p-2)

Math
Basic MathA long year-end status report for work is 82 pages long. You need to print 19 copies for a meeting next week. How much is the paper going to cost for those reports? Paper is sold in reams (500 pages) for $3.99 each. Give your answer to the nearest cent, only for the paper you use (partial reams are OK)

Math
Basic MathEvery year in Delaware there is a contest where people create cannons and catapults designed to launch pumpkins as far in the air as possible. The equation y = 15 + 110x -16x² can be used to represent the height, y, of a launched pumpkin, where x is the time in seconds that the pumpkin has been in the air. What is the maximum height that the pumpkin reaches? How many seconds have passed when the pumpkin hits the ground? (Hint: If the pumpkin hits the ground, its height is 0 feet.)
Math
Basic MathBrandon is analyzing the profits from two of his restaurant locations. The first location showed a profit of $3,000 in the first week of the year but has a showed a steady decrease in profits of 1.5% each week since then.
His second location showed a profit of $1,500 in the first week of the year and has showed a steady increase in profits of 1.2% each week since then.
Which system of equations can Brandon use to determine the number of weeks, x, until the profits, y, from the two locations are the same?
A. y = 3,000 (1.015)^x
y = 1,500 (1.012)^x
B. y = 3,000(0.985)^x
y = 1,500(1.012)^x
C. y = -3,000 (1.015)^x
y = 1,500(1.012)^x
D. y = -3,000(0.985)^x
Y = 1,500/(1,012)^x

Math
Basic MathAlma bought a laptop computer at a store that gave a 20 percent discount off its original price. The total amount she paid to the cashier was p dollars, including an 8 percent sales tax on the discounted price. Which of the following represents the original price of the computer in terms of p?
A) 0.88p
B) p / 0.88
C) (0.8) (1.08) p
D) p / (0.8) (1.08)
Math
Basic MathComplete this expression. Assume that any variables are not equal to zero.
z⁰ =
Simplify the following expression completely.
(5w+2)⁰ =
Simplify the following.
3⁰ =
Simplify the following.
0⁴ =

Math
Basic MathFactor each trinomial. Then match the polynomial (term) on the left with its factored form (definition) on the right.
Column A Column B
1. x²-8x-20 a. Prime
2. x²+8x-20 b. (x-2)(x+10)
3. x² - x-20 c. (x-10)(x + 2)
4. x²-9x-20 d. (x - 5)(x+4)

Math
Basic MathThe function h defined by h(t) + (49+4.9t) (10-t) models the height, in meters, of an object t seconds after it is dropped from a helicopter.
From what height is the object dropped?
a 500
b 490
c 480
d 460

Math
Basic MathA car company tested a sports car on a road with different inclines. The test driver tested the car by driving a distance of x miles on a flat road,
(x² + 3) miles downhill, and (x-7) miles uphill. Which simplified expression is equivalent to the total distance, in miles, for which the car was
tested? (2 points)
a. 3x²-4
b. 3x² +10
c. x²+2x-4
d. x²+2x+10

Math
Basic MathAnswer the following.
(a) The total surface area of Asia is approximately 17,200,000 square miles. Write this number in scientific notation.
(b) The signal from a certain satellite takes approximately 4.1 x 10^-2 seconds to reach Earth. Write this number in standard notation.
Math
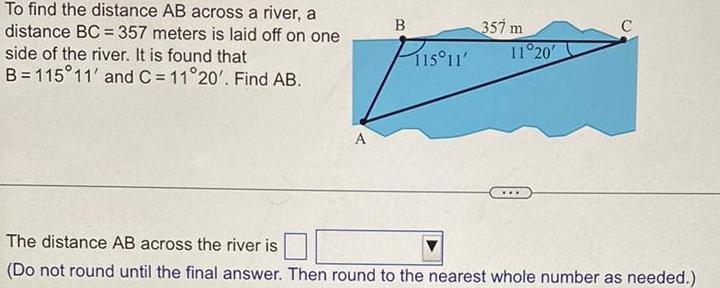
Basic MathTo find the distance AB across a river, a distance BC= 357 meters is laid off on one side of the river. It is found that B=115°11' and C = 11°20'. Find AB.
The distance AB across the river is
(Do not round until the final answer. Then round to the nearest whole number as needed.)

Math
Basic MathConsider the curve given parametrically by
x=4-t², y = t³ - 3t.
(a) List all of the points (x, y) where the tangent line is horizontal.
(b) List all of the points (x, y) where the tangent line is vertical.
Math
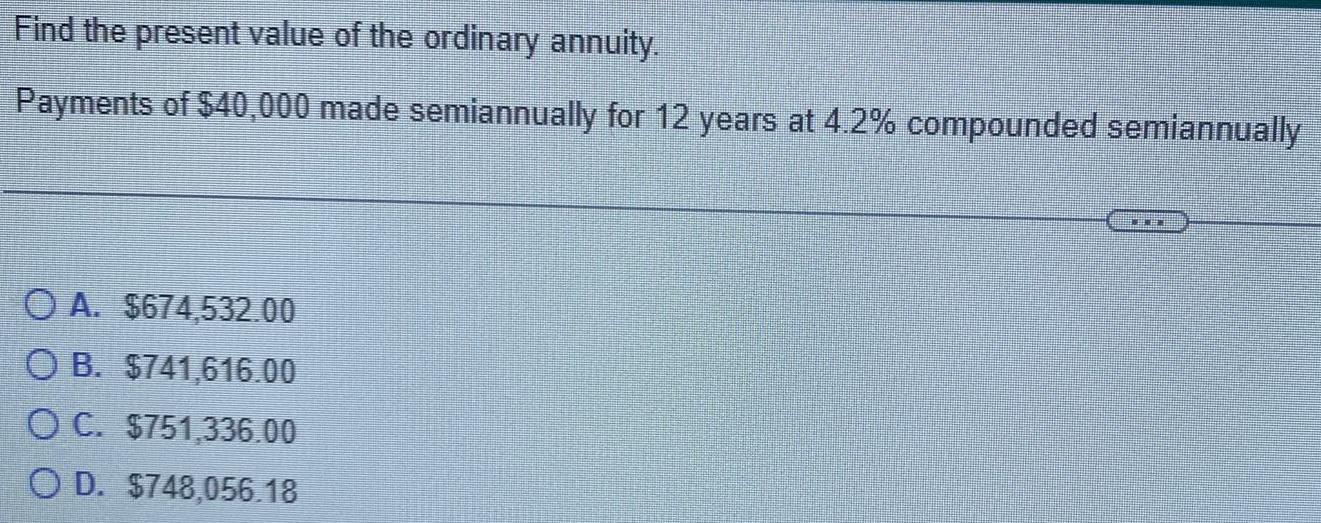
Basic MathFind the present value of the ordinary annuity.
Payments of $40,000 made semiannually for 12 years at 4.2% compounded semiannually
A. $674,532.00
B. $741,616.00
C. $751,336.00
D. $748,056.18

Math
Basic MathThe half-life of radium-223 is approximately 11.43 days.
How much of an 8 gram sample of radium-223 would remain after 3 days? Round to three decimal places.

Math
Basic MathAt the beginning of an experiment, a scientist has 304 grams of radioactive goo. After 180 minutes, her sample has decayed to 19 grams.
What is the half-life of the goo in minutes?
Find a formula for G(t), the amount of goo remaining at time t.
G(t) =
How many grams of goo will remain after 14 minutes?
You may enter the exact value or round to 2 decimal places.