Logarithms Questions and Answers
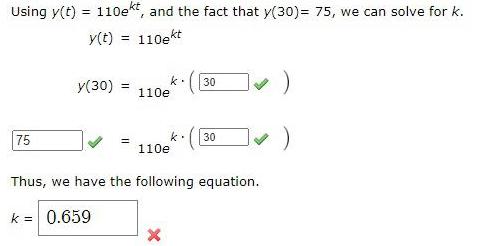
Math
LogarithmsUsing y(t) = 110ekt, and the fact that y(30)= 75, we can solve for k.
y(t) = 110ekt
y(30) =110ek.
=110ek
Thus, we have the following equation.
k =

Math
LogarithmsExpand the logarithm as much as possible by rewriting it as a sum, difference, or product of logarithms.
log4(x/z / w)

Math
LogarithmsRewrite the expression as an equivalent ratio of logs using the indicated base.
log13 (57.25) to base 10

Math
LogarithmsThe half-life of a certain tranquilizer in the bloodstream is 34 hours. How long will it take for the drug to decay to 87% of the original dosage? Use the exponential decay model, A=A0ekt, to solve.
hours
(Round to one decimal place as needed.)
Math
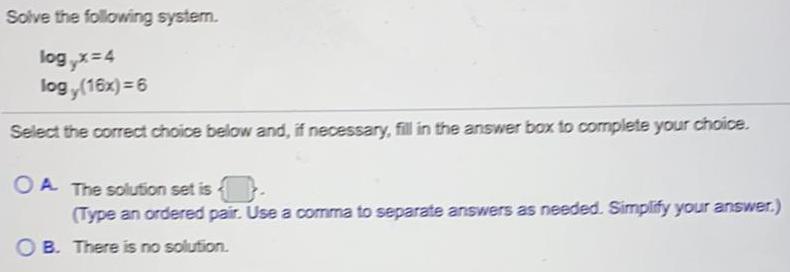
LogarithmsSolve the following system.
logy x=4
logy (16x) = 6
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A The solution set is
(Type an ordered pair. Use a comma to separate answers as needed. Simplify your answer.)
B. There is no solution.
Math
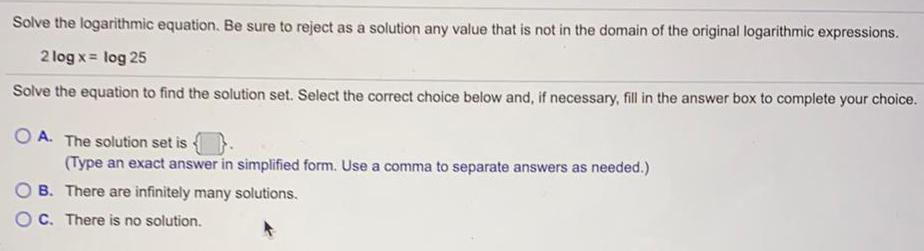
LogarithmsSolve the logarithmic equation. Be sure to reject as a solution any value that is not in the domain of the original logarithmic expressions.
2 log x = log 25
Solve the equation to find the solution set. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Type an exact answer in simplified form. Use a comma to separate answers as needed.)
B. There are infinitely many solutions.
C. There is no solution.
Math
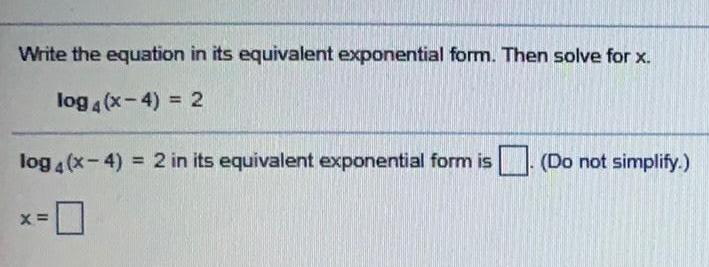
LogarithmsWrite the equation in its equivalent exponential form. Then solve for x.
log 4(x-4) = 2
log 4(x-4) = 2 in its equivalent exponential form is. (Do not simplify.)
x=

Math
LogarithmsWhich of the following is the inverse of y=12x?
y = log1/12 x
y = log12 1/x
y=logx12
y = log12X

Math
LogarithmsSuppose that the number of bacteria in a certain population increases according to a continuous exponential growth model. A sample of 1400 bacteria selected from this population reached the size of 1849 bacteria in six hours. Find the hourly growth rate parameter.
Note: This is a continuous exponential growth model.
Write your answer as a percentage. Do not round any intermediate computations, and round your percentage to the nearest hundredth.

Math
LogarithmsUse the Change of Base Formula to evaluate log4 27. Then convert log4 27 to a logarithm in base 2. Round to the nearest thousandth.
3.296; log₂ 5.196
2.377; log₂ 13.5
2.377; log₂ 5.196
1.431; log₂ 13.5

Math
LogarithmsSuppose a house that costs $270,000 appreciates by 5% each year. In about how many years will the house be worth $350,000? Use the equation 350 = (270)(1.05)* and round the value of x to the nearest year.
6
5
7
4

Math
LogarithmsSuppose a new car that costs $25,000 depreciates by 12% each year. In about how many years will the car be worth $15,000? Use the equation 15,000 = (25,000)(0.88)^x and round the value of x to the nearest year.
7
4
5
6

Math
LogarithmsThe population of a certain city was 3,674 in 1995. It is expected to decrease by about 0.31% per year. Write an exponential decay function, and use it to approximate the population in 2020. The exponential decay function where f(x) is the population of the city x years after 1995 is f(x) =
![Identify the error in the student solution shown below. Find the correct answer.
2ln(x) = In(3x) - [In(9) - 2ln(3)]
In(x²)= In(3x) - [In(9) - In(9)]
In(x²)= In(3x)-0
In(x²)= In(3x/0); division by 0, undefined.](https://media.kunduz.com/media/sug-question/raw/47424306-1658323679.4153912.jpeg?w=256)
Math
LogarithmsIdentify the error in the student solution shown below. Find the correct answer.
2ln(x) = In(3x) - [In(9) - 2ln(3)]
In(x²)= In(3x) - [In(9) - In(9)]
In(x²)= In(3x)-0
In(x²)= In(3x/0); division by 0, undefined.
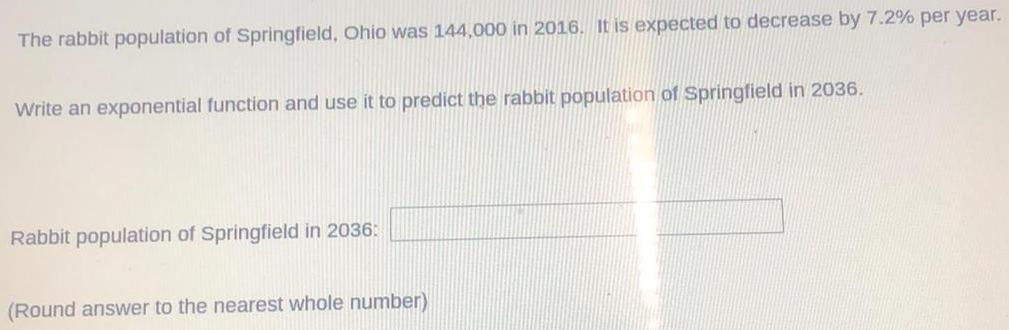
Math
LogarithmsThe rabbit population of Springfield, Ohio was 144,000 in 2016. It is expected to decrease by 7.2% per year.
Write an exponential function and use it to predict the rabbit population of Springfield in 2036.
Rabbit population of Springfield in 2036:


Math
LogarithmsA wooden artifact from an ancient tomb contains 55 percent of the carbon-14 that is present in living trees. How long ago, to the nearest year, was the artifact made? (The half-life of carbon-14 is 5730 years.) years
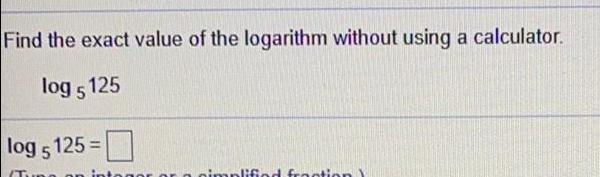

Math
LogarithmsA wooden artifact from an ancient tomb contains 35 percent of the carbon-14 that is present in living trees. How long ago, to the nearest year, was the artifact made? (The half-life of carbon-14 is 5730 years.)

Math
LogarithmsLet P(t) = 30000 (1.03)t be the population of a town t years after the year 2000.
Estimate in which year the population will reach 32782.
Year =
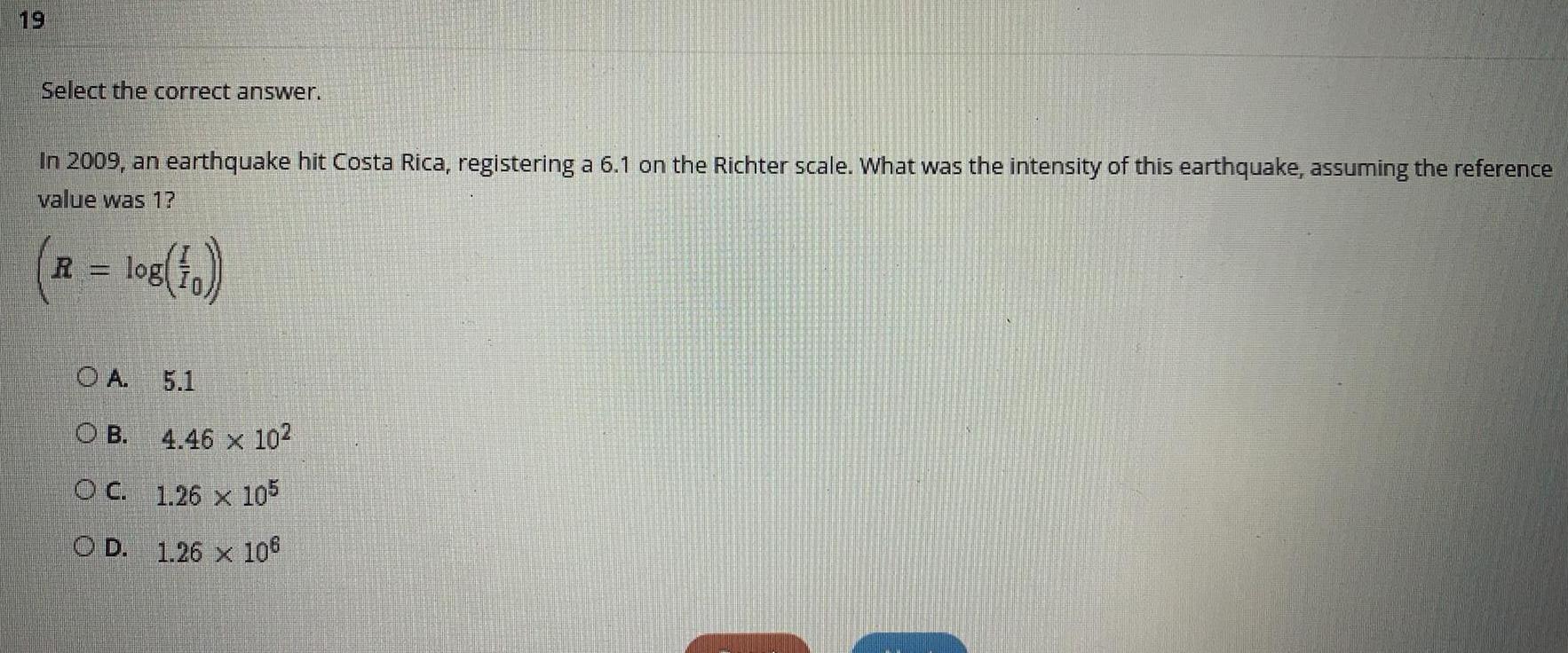
Math
LogarithmsIn 2009, an earthquake hit Costa Rica, registering a 6.1 on the Richter scale. What was the intensity of this earthquake, assuming the reference value was 1?
(R =log(I/I₀))
A. 5.1
B. 4.46 x 10^2
C. 1.26 x 10^5
D. 1.26 x 10^6

Math
LogarithmsIn a learning theory project, psychologists discovered that
f(t) = 0.8 / (1+e^-0.2t)
is a model for describing the proportion of correct responses, f(t), after t learning trials.
a. Find the proportion of correct responses prior to learning trials taking place.
b. Find the proportion of correct responses after 10 learning trials.
c. What is the limiting size of f(t), the proportion of correct responses, as continued learning trials take place?

Math
Logarithms1. The logistic growth function f(t) = 100,00 / (1 + 5000e-t) describes the number of people, f(t), who have become ill with influenza t weeks after its initial outbreak in a particular community.
a. How many people became ill with the flu when the epidemic began?
b. How many people were ill by the end of the fourth week?
c. What is the limiting size of the population that becomes ill?
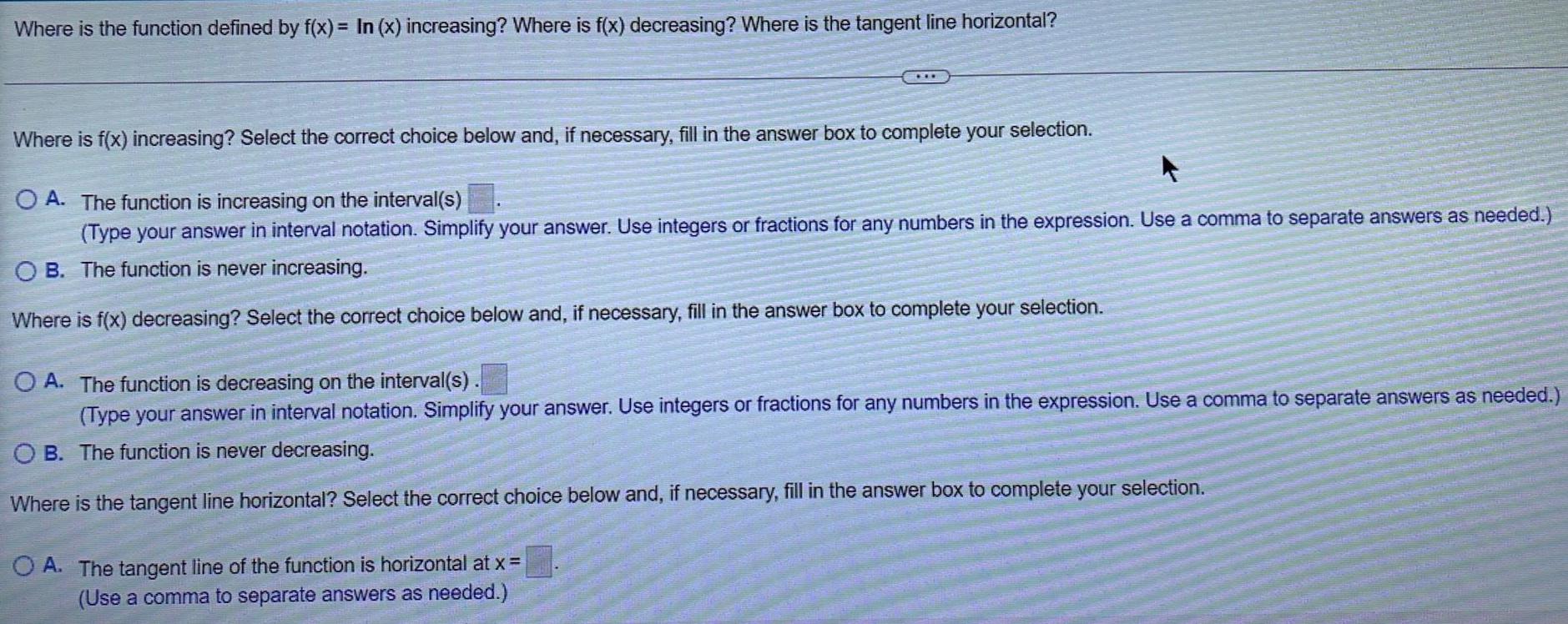
Math
LogarithmsWhere is the function defined by f(x)= In (x) increasing? Where is f(x) decreasing? Where is the tangent line horizontal?
Where is f(x) increasing? Select the correct choice below and, if necessary, fill in the answer box to complete your selection.
A. The function is increasing on the interval(s)
(Type your answer in interval notation. Simplify your answer. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)
B. The function is never increasing.
Where is f(x) decreasing? Select the correct choice below and, if necessary, fill in the answer box to complete your selection.
A. The function is decreasing on the interval(s).
(Type your answer in interval notation. Simplify your answer. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)
B. The function is never decreasing.
Where is the tangent line horizontal? Select the correct choice below and, if necessary, fill in the answer box to complete your selection.
A. The tangent line of the function is horizontal at x =
(Use a comma to separate answers as needed.)

Math
LogarithmsUse properties of logarithms to rewrite the given expression as the logarithm of a single quantity, then enter that single quantity in the answer box to complete the expression.
2 logb (x) + 2logb (y)
logb( )
Math
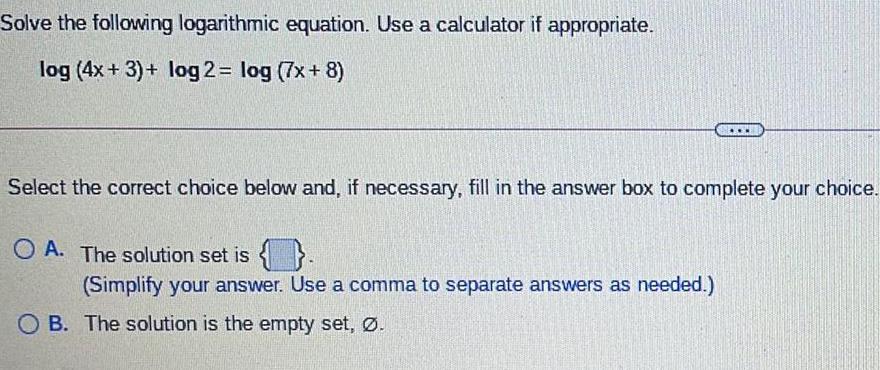
LogarithmsSolve the following logarithmic equation. Use a calculator if appropriate.
log (4x+3)+ log 2 = log (7x+8)
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is { }.
(Simplify your answer. Use a comma to separate answers as needed.)
B. The solution is the empty set, Ø.
Math
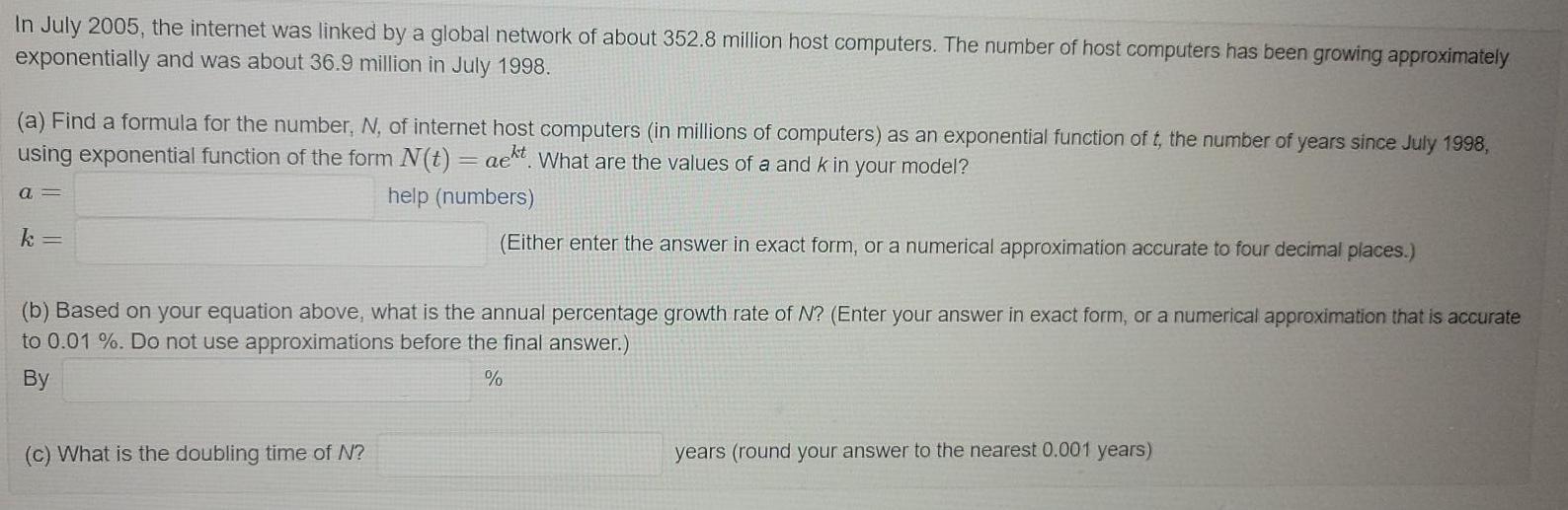
LogarithmsIn July 2005, the internet was linked by a global network of about 352.8 million host computers. The number of host computers has been growing approximately
exponentially and was about 36.9 million in July 1998.
(a) Find a formula for the number, N, of internet host computers (in millions of computers) as an exponential function of t, the number of years since July 1998,
using exponential function of the form N(t) = aet. What are the values of a and k in your model?
help (numbers)
a =
k=
(Either enter the answer in exact form, or a numerical approximation accurate to four decimal places.)
(b) Based on your equation above, what is the annual percentage growth rate of N? (Enter your answer in exact form, or a numerical approximation that is accurate
to 0.01 %. Do not use approximations before the final answer.)
%
By
(c) What is the doubling time of N?
years (round your answer to the nearest 0.001 years)
Math
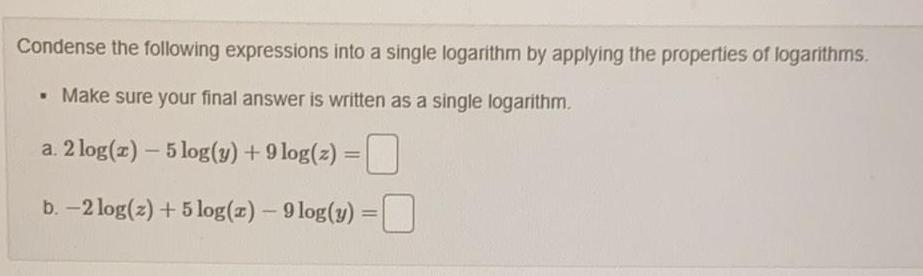
LogarithmsCondense the following expressions into a single logarithm by applying the properties of logarithms.
Make sure your final answer is written as a single logarithm.
a. 2 log(x) - 5 log(y) + 9 log(z) =
b. -2 log(z) + 5log(x) - 9 log(y) =
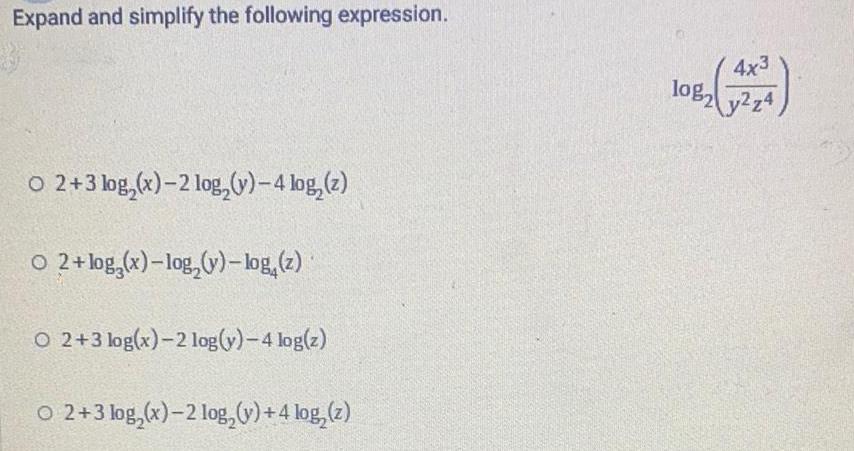
Math
LogarithmsExpand and simplify the following expression.
log₂ (4x3/y2z4)
2+3 log₂ (x)-2 log2(y)-4 log2(z)
2+log3(x)-log2(v)-log4(z)
2+3 log3(x)-2 log(y) - 4 log(z)
2+3 log2(x)-2 log2(v) +4 log2(z)

Math
LogarithmsObtain an approximate value for the logarithm using natural logarithms.
log 5313
log 5313
(Round to three decimal places as needed.)

Math
Logarithms(a) Solve the equation 1500(0.733)t = 300 using the In function.
Round your answer to three decimal places.
(b) Solve the equation 1500 (0.733)t = 300 using the log function.
Round your answer to three decimal places.

Math
LogarithmsA certain culture of bacteria initially has 10 bacteria
and is observed to double every 1.5 hours.
a. Find an exponential model n(t) =n0*2¹/a for the
number of bacteria in the culture after t hours.
b. Estimate the number of bacteria after 35 hours.
c. After how many hours will the bacteria count
reach 10,000?
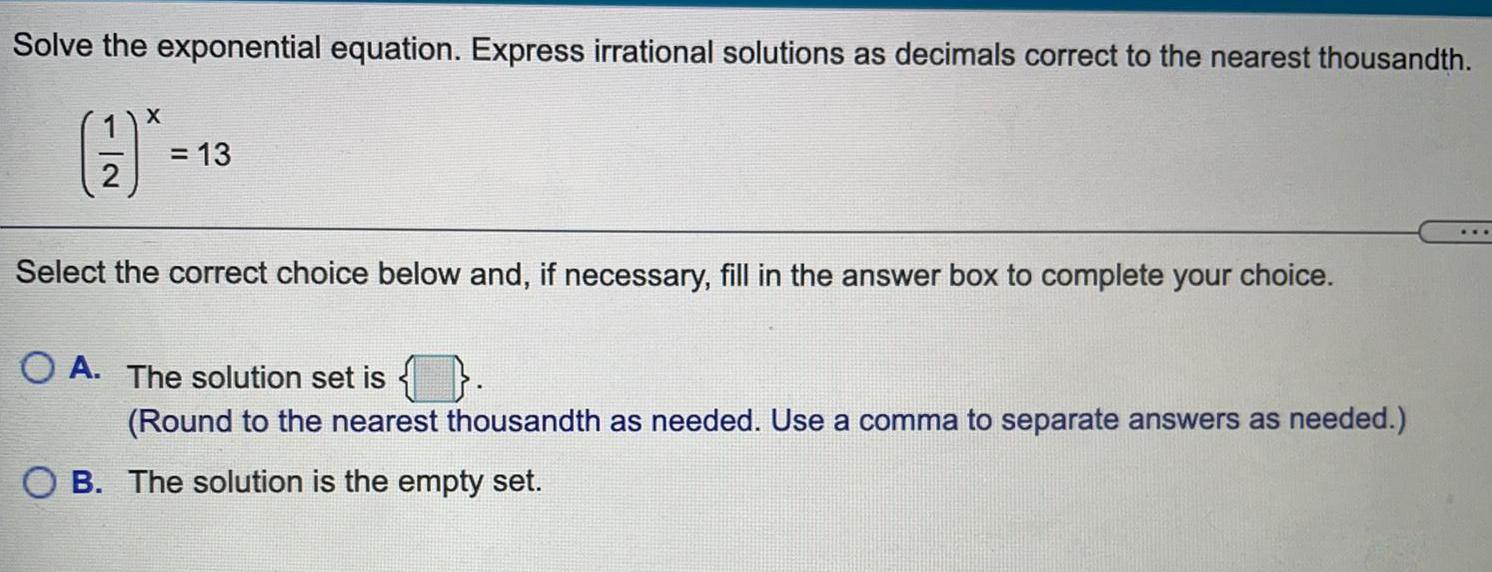
Math
LogarithmsSolve the exponential equation. Express irrational solutions as decimals correct to the nearest thousandth.
(1/2)x = 13
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Round to the nearest thousandth as needed. Use a comma to separate answers as needed.)
B. The solution is the empty set.

Math
LogarithmsSolve the equation. Write the answer in terms of the natural logarithm.
e9x + 4 = 6
The solution set is.
(Type an exact answer in simplified form. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)

Math
LogarithmsExpress the following equations in logarithmic form:
(a) 5^4 = 625 is equivalent to the logarithmic equation:
(b) 10^ 3 =0.001 is equivalent to the logarithmic equation:

Math
LogarithmsRewrite the expression e^5 ln(x) so that no exponential or logarithmic functions are involved. The formula b^ln t = r and the basic rules of exponents will be helpful. Assume that x and y are positive.

Math
LogarithmsChoose a number between 0 and 100 for k. Enter your number in the blank so I know what to use for grading. k=__. Rewrite each exponential equation in logarithmic form. Hint: Use Control and, to do a base of logarithm and Control and . to do an exponent.
18. e^k = v
19. K = 10^x
20. k^x=8

Math
LogarithmsUse logarithms to solve the given equation. (Round the answer to four decimal places.)
3^-2x = 43
X=

Math
LogarithmsFind the associated exponential decay or growth model. (Round all coefficients to three significant digits.)
Q = 1,600 when t = 0; half-life = 1
Q =

Math
LogarithmsThe yield V (in millions of cubic feet per acre) for a stand of timber at age t is
V = 6.8e^(-4.85)/t
where t is measured in years.
(a) Find the limiting volume of wood per acre as t approaches infinity.
million ft³/acre
(b) Find the rates at which the yield is changing when t = 40 and t = 50. (Round your answers to three decimal places.)
when t 40 years million ft³/acre/yr
when t= 50 years million ft³/acre/yr

Math
LogarithmsSolve the given equation for the variable. (Round your answers to four decimal places. Enter your answers as a comma-separated list.)
10,000 = 700(1.04^8t + 1)
t =

Math
LogarithmsA bacteria doubles every 6 hours. If the initial population is 50, after how many hours will the population
reach 1,000? Express your answer as a decimal rounded to the nearest hundredth.
hours
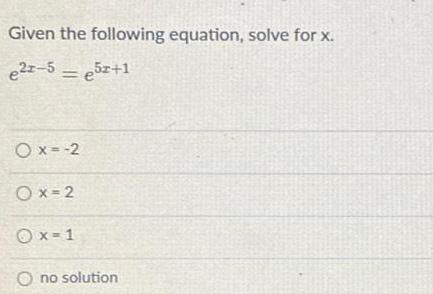


Math
LogarithmsUse properties of logarithms to expand each logarithmic expression as much as possible. Evaluate logarithmic expressions without using a calculator if possible.

Math
LogarithmsThe given function y is positive for all x greater than three. Hence, the function In y is ---Select--- in the domain of x. Obtain the natural logarithm of the function y, using the logarithmic properties
In ab = In a + In b and In(2) = In a ? In b, where a and b are positive.
In y = In(x + 1)? In(x - 3) In(x - 1) In(x + 3)
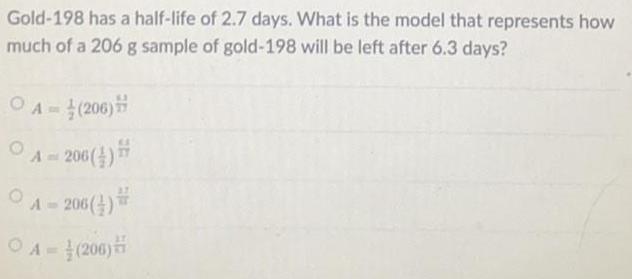
Math
LogarithmsGold-198 has a half-life of 2.7 days. What is the model that represents how
much of a 206 g sample of gold-198 will be left after 6.3 days?
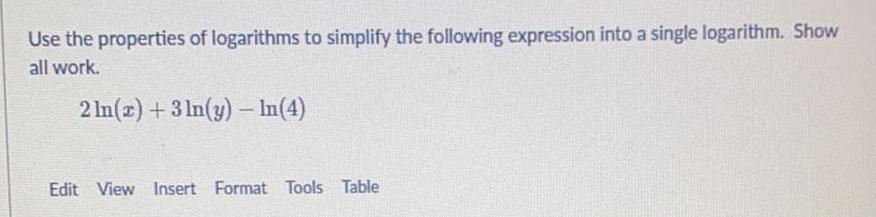
Math
LogarithmsUse the properties of logarithms to simplify the following expression into a single logarithm. Show
all work.
2 ln(x) + 3 ln(y) - In(4)
Edit View Insert Format Tools Table
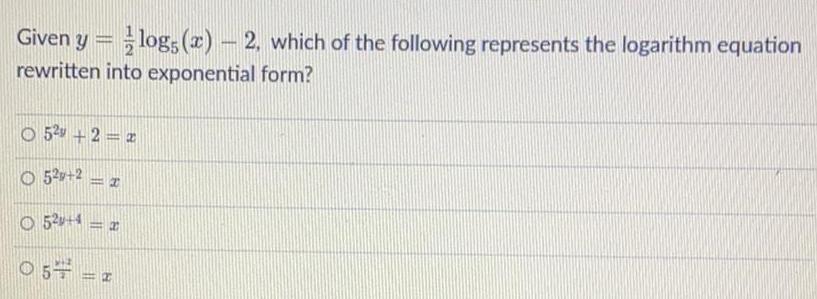
Math
LogarithmsGiven y = 1/2 log5 (x) - 2, which of the following represents the logarithm equation rewritten into exponential form?
5^2y +2=x
5^2y+2 = x
5^2y+4= x
5^y+2/2 = x
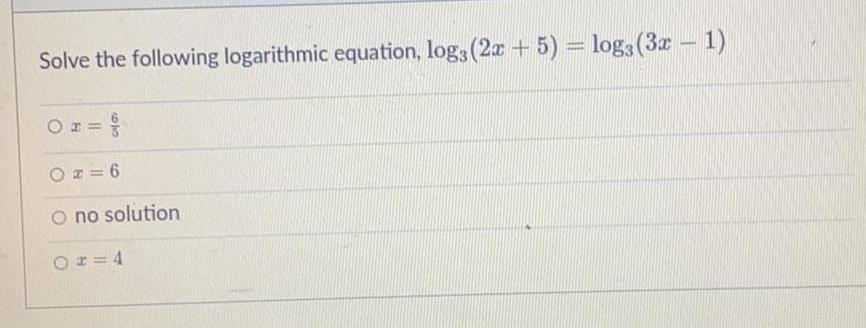
Math
LogarithmsSolve the following logarithmic equation, log, (2x + 5) = log3 (3x - 1)
x = 6/5
x = 6
no solution
x = 4