Quadratic equations Questions and Answers

Math
Quadratic equationsSelect the correct labeling of a, b, and c to the standard form of the quadratic equation.
a = 4, b = -2, and c = 7
4x² + 5x - 2 = 0
x² + 2x-5 = 0
x²-5=0
4x² - 2x +7=0
x² + 2x = 0

Math
Quadratic equationsWhat are the solutions to 2(x-7)² = 32?
A x = 7 ± √32
B x=± √65
X=
C x = 3 and x = 11
D x = -1 and x = 15

Math
Quadratic equationsConsider the following quadratic function.
g(x)=2x²-16x+37
(a) Write the equation in the form g (x)= a (x-h)²+k. Then give the vertex of its graph.
Writing in the form specified: g(x) =
Vertex:
(b) Graph the function. To do this, plot five points on the graph of the function: the vertex, two points to the left of the ver vertex. Then click on the graph-a-function button.

Math
Quadratic equationsFor the polynomial below, -3 is a zero.
g(x)=x³ + 5x² + 16x + 30
Express g (x) as a product of linear factors.
g(x) = 0

Math
Quadratic equationsUsing the axis of symmetry formula, find the axis of symmetry and vertex for each equation.
3. y=-x² +10x-26
4. y=3x² - 6x
5. y=2x² - 4

Math
Quadratic equationsIf the roots of the equation x² - 6x = 27 are p and t, and if t < p, then p =
1/t
t2
2t
-t
t+6


Math
Quadratic equationsCompute the discriminant. Then determine the number and type of solutions of the given equation.
x^2-4x-6=0
What is the discriminant?
(Simplify your answer.)
Choose the sentence that describes the number and type of solutions of the quadratic equation.
A. There are two imaginary solutions.
B. There are two unequal real solutions.
C. There is one real solution.
D. There are an infinite number of real solutions.

Math
Quadratic equationsSolve the equation by factoring.
x² = 6x +27
Rewrite the equation in factored form.
(x+3)(x-9) = 0
(Factor completely.)
The solution set is

Math
Quadratic equationsSolve the quadratic equation using the square root property.
(x-7)² = -3
The solution set is
(Simplify your answer. Type an exact answer, using radicals as needed. Express complex numbers in terms of i. Use a comma to separate answers as needed.)

Math
Quadratic equationsSolve the quadratic equation by completing the square x² +6x+4=0. To complete the square, what number should be added to both sides of the equation?

Math
Quadratic equationsSolve the quadratic equation by completing the square.
x² - 10x+12=0
First, choose the appropriate form and fill in the blanks with the correct numbers.
Then, solve the equation. If there is more than one solution, separate them with commas.
Form:
Solution:

Math
Quadratic equationsIf using the method of completing the square to solve the quadratic equation x² + 8x + 37 = 0, which number would have to be added to "complete the square"?

Math
Quadratic equationsAndrea simplified a polynomial expression. The solution was 4x²-7x + 5.
Which of the following could have been the original expressions?
SELECT ALL THAT APPLY.
(3x²-9x+8)+(x²+2x-3)
(2x² - 4x-5)-(-2x² + 3x - 10)
(5x²-2)-(x²+7x+3)
(4x² + 3x) -(10x + 5)

Math
Quadratic equationsThe polynomial function g is defined by g(x)=-x-5x³-4x² + 4x-1.
Use the ALEKS graphing calculator to find all the points (x, g(x)) where there is a local maximum.


Math
Quadratic equationsx2+5 – 2
When trying to factor, Sarita says this polynomial is PRIME.
Why is she correct?
there are no numbers with a product of -2, and a sum of 5
there are no numbers with a product 5, and a sum of -2
both 5 and -2 are prime numbers

Math
Quadratic equationsSolve the quadratic equation by completing the square.
x² +8x+14=0
First, choose the appropriate form and fill in the blanks with the correct numbers.
Then, solve the equation. If there is more than one solution, separate them with commas.
Form:

Math
Quadratic equationsWhich of the following is an attribute of any quadratic function?
It has a constant rate of change.
The function values increase as x increases.
It is symmetric about a line through its vertex.
The graph always intersects the x-axis twice.

Math
Quadratic equationsA paper airplane is thrown from a height of 9 feet. The function
y = -2x² + 3x +9 represents the path of the plane, where x is the
distance traveled and H(x) is the height of the plane.
At what distance does the plane hit the ground?
18 ft
3 ft
2 ft
9 ft

Math
Quadratic equationsThe height in feet of a ball thrown in the air from a ledge 112 feet high is
represented by the function f(x) = -16x²+96x +112, where x is the number
of seconds since the ball has been thrown.
How many seconds does it take the ball to reach the ground?
256
7
3
112

Math
Quadratic equationsCarter found the discriminant of this quadratic function.
F(x)=6x²-5x +3
According to the discriminant, which best describes the roots of F(x)?
One real root
Two real roots
Two complex roots
One complex root

Math
Quadratic equationsPut the quadratic into vertex form and state the coordinates of the vertex.
y = x² − 6x + 8
Vertex Form: y =
Vertex:

Math
Quadratic equationsWhich equation has the same solution as x² + 18x - 20 = -2?
(x-9)² = 99
(x + 9)² = -63
○ (x + 9)² = 99
(x - 9)² = -63

Math
Quadratic equationsAlton and Eithan are each saving money for a car. The total amount of money Alton will save is given by the function f (x) = = 43 + 3x. The total amount of money Eithan will save is given by the functiong (x) = x² + 25. After how many weeks, x, will they have the same amount of money saved? Explain how you arrived at your answer.

Math
Quadratic equationsSolve the equation below by completing the square and then solving for x.
2x²-28x-2=-50
A. x= 2 or x = -18
B. x = 7 or x = 4
C. x = 2 or x = 12
D. x = -7 or x = 4

Math
Quadratic equationsThe polynomial given below has___root(s).
3x²-8x+4
A. two positive
B. two complex
C. two negative
D. one positive and one negative

Math
Quadratic equationsWhat number would you add to complete the square for the equation below?
x² + 6x = 0
Math
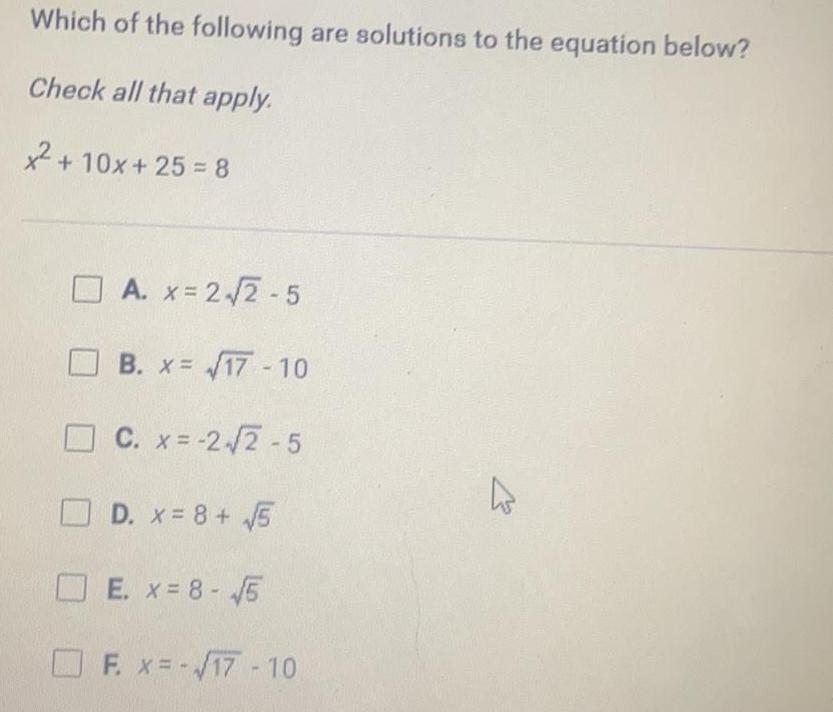
Quadratic equationsWhich of the following are solutions to the equation below?
Check all that apply.
x² + 10x + 25 = 8
A. x = 2√2-5
B. x = √17-10
C. x = -2-√√2-5
D. x = 8 + √√5
E. x = 8 - √5
F. x = -√17-10

Math
Quadratic equationsA child launches a toy rocket in the air, and the function f(x) = -10x² +90x+ 20 represents the flight of the rocket, where x is the time in seconds and f(x) is the height (in feet) at x seconds.
a. For how many seconds is the rocket higher than 100 feet above the ground?
b. Explain how you found your answer.
Math
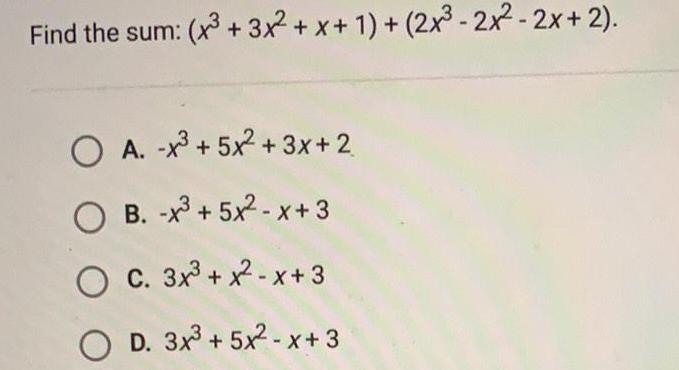
Quadratic equationsFind the sum: (x³ + 3x²+x+1)+ (2x³ - 2x² - 2x+2).
A. x³ +5x²+3x+2
B. -x³ +5x²-x+3
C. 3x³ + x²-x+3
D. 3x³ + 5x²-x+3

Math
Quadratic equationsWhat number must you add to the polynomial below to complete the square?
x²-26x


Math
Quadratic equations6/x= 2x+4/5 Multiply each side by the common denominator to find the quadratic equation equivalent to this equation.
A. x² + 4x-15 = 0
B. 2x² + 4x-30 = 0
C. x² + 4x-30 = 0
D. 2x² + 4x + 15 = 0
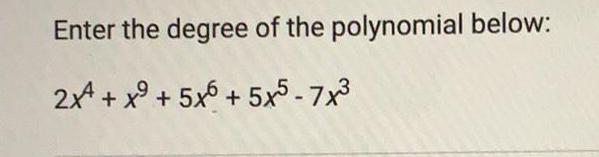
Math
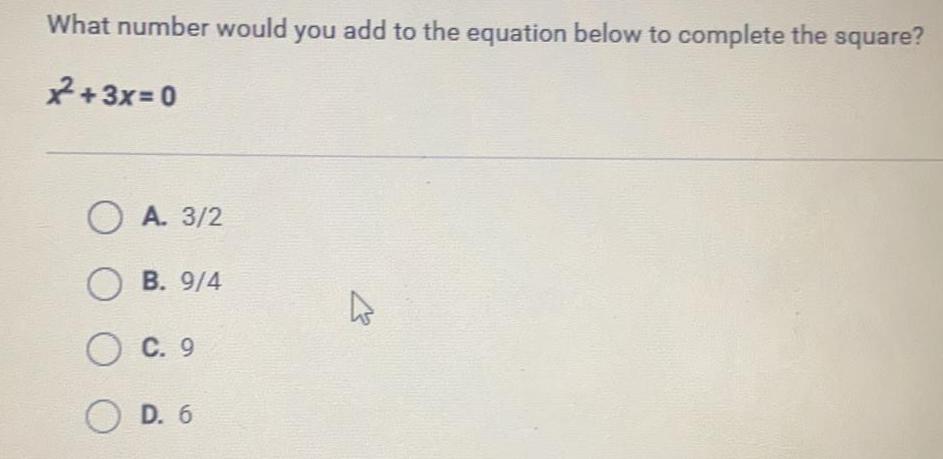
Quadratic equationsWhat number would you add to the equation below to complete the square?
x^2+3x=0
A. 3/2
B. 9/4
C. 9
D. 6

Math
Quadratic equationsThe ________ is the name of the number under the radical symbol in the quadratic formula.


Math
Quadratic equationsFind the product and enter it in the box below. Enter your answer as a
polynomial in descending order and use the caret (^) for exponents. For
example, you would write 4x2 as 4x^2.
(5x+1)(5x+8)

Math
Quadratic equationsFind all ordered pair solution (s) to the system of nonlinear equations given by:
y=-x-5
y = x² - 5
If there is more than one solution, enter as a list of ordered pairs. Example: (2,-5), (5,-2)

Math
Quadratic equationsGiven the following quadratic equation, state the x and y intercepts (solutions of the form (x, 0) and (0, y)), the vertex, and then use this information to sketch the graph:
a) y = x² - 2x-3
b) y = x² + 2x
c) y = -x² + 4x-2

Math
Quadratic equationsThe points (0, 2), (1, 3), (2, 6), and (3, 11) are on the graph of a function. Which of the following equations represents that function?
A h(x) = 0.5x² +1.5
B. h(x) = x² + 2
C. h(x) = x + 2
D. h(x) = 2x²

Math
Quadratic equationsA ball was thrown upward into the air. The height, in feet, of the ball above the ground t seconds after being thrown can be determined by the expression -16t^2 + 40t + 3. What is the meaning of the 3 in the expression?
A. The ball was thrown from a height of 3 feet.
B. The ball took 3 seconds to reach the ground.
C. The ball reached a maximum height of 3 feet.
D. The ball took 3 seconds to reach its maximum height.

Math
Quadratic equationsDetermine whether the quadratic function shown below has a
minimum or maximum, then determine the minimum or maximum
value of the function.
The
ƒ(x) = x² + 4x − 1

Math
Quadratic equationsWrite the quadratic function in the form g(x)= a (x −h)² + k.
Then, give the vertex of its graph.
g(x)=x² + 4x +3

Math
Quadratic equationsFind all real solutions of the equation (9x + 2)² = 36.
Write your answers as a list of integers or reduced fractions in the form A/B. For example, if your answers are 2/3 and 5, you would enter 2/3,5

Math
Quadratic equationsFind all real solutions of equation 4x² + 5x - 4 = 0.
Does the equation have real solutions? Input Yes or No:
If your answer is Yes, input the solutions:


Math
Quadratic equationsConsider the parabola given by the equation:
Find the following for this parabola:
y = x² + 6x - 8
A) The vertex =
B) The y intercept is the point (0,
C) Find the two values of that correspond to the x intercepts of the parabola and write them as a list, separated by commas:
x =
Round your answer(s) to two decimal places.

Math
Quadratic equationsConsider the parabola given by the equation:
f(x)=x²-12x + 13
Find the following for this parabola:
A) The value of f(-5):
B) The vertex =
C) The y intercept is the point (0,
D) Find the two values of a that make f(x) = 0. Round your answers to two decimal places. Write the values as a list, separated by commas: