Sets and Relations Questions and Answers

Math
Sets and RelationsList all the subsets of the given set.
{tangerine, blueberry, kiwifruit)
Choose the answer that lists all of the subsets of {tangerine, blueberry, kiwifruit).
A. {tangerine}, {blueberry}, {kiwifruit}, {tangerine, blueberry},
{tangerine, kiwifruit}, {blueberry, kiwifruit}
B. {} , {tangerine}, {blueberry}, {kiwifruit}, {tangerine, blueberry},
{tangerine, kiwifruit}, {blueberry, kiwifruit},
{tangerine, blueberry, kiwifruit}
C. {} , {tangerine}, {blueberry}, {kiwifruit}, {tangerine, blueberry},
{tangerine, kiwifruit}, {blueberry, kiwifruit}
D. {tangerine}, {blueberry}, {kiwifruit}, {tangerine, blueberry},
{tangerine, kiwifruit}, {blueberry, kiwifruit},
{tangerine, blueberry, kiwifruit}
Math
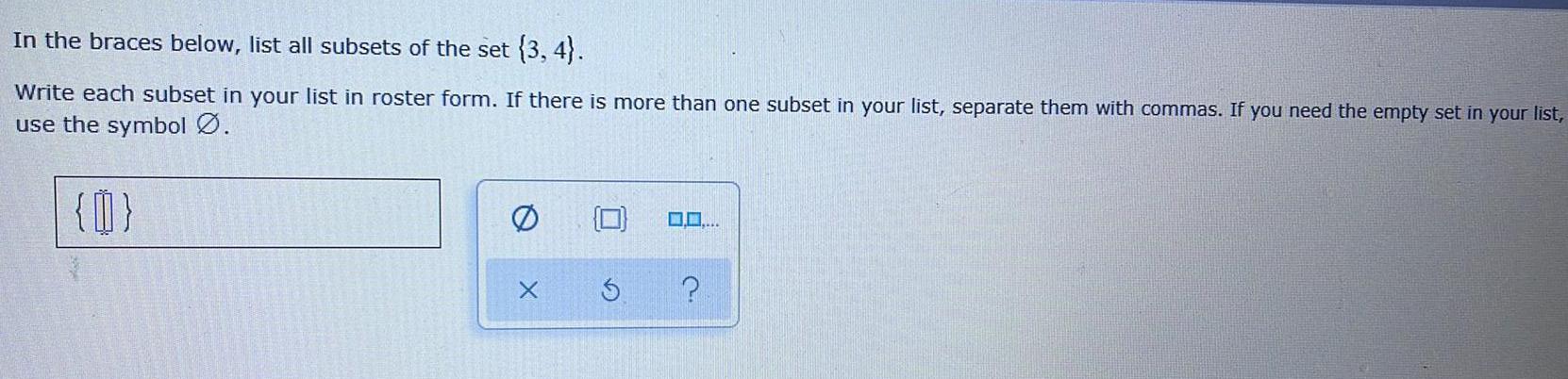
Sets and RelationsIn the braces below, list all subsets of the set (3, 4). Write each subset in your list in roster form. If there is more than one subset in your list, separate them with commas. If you need the empty set in your list, use the symbol Ø.
Math
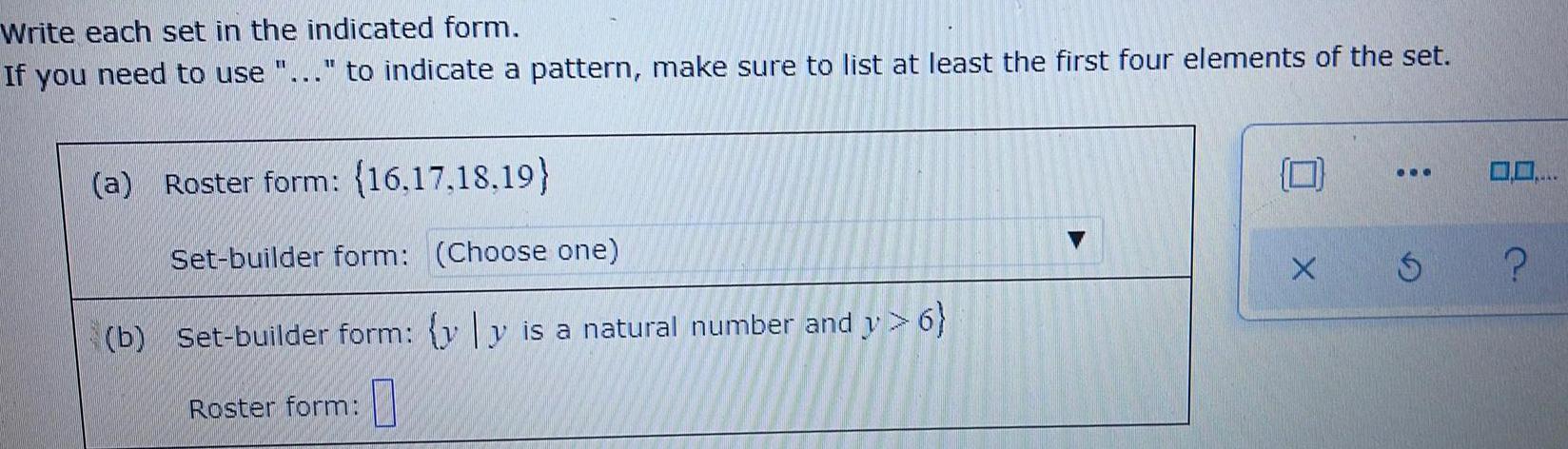
Sets and RelationsWrite each set in the indicated form.
If you need to use "..." to indicate a pattern, make sure to list at least the first four elements of the set.
(a) Roster form: (16,17,18,19)
Set-builder form: (Choose one)
(b) Set-builder form: {yy is a natural number and y> 6}
Roster form:

Math
Sets and RelationsTwo cars leave the origin at noon. One goes north at 50 mph and the other goes east at 60 mph. Express the distance between the cars in terms of t, the number of hours they have been driving.

Math
Sets and RelationsFor each of the following discriminant state what it indicates about the number of roots of the quadratic equation and sketch a possible graph.
a. b2 - 4ac = 5
b. b² - 4ac = 0
c. b² - 4ac = -10

Math
Sets and RelationsJim owns a vehicle. Select all of the mutually exclusive events from the following events.
Jim's vehicle is a van.
Jim's vehicle is a motorcycle.
Jim's vehicle has Texas license plates.
Jim's vehicle is red.
Jim's vehicle is a sport utility vehicle (SUV).
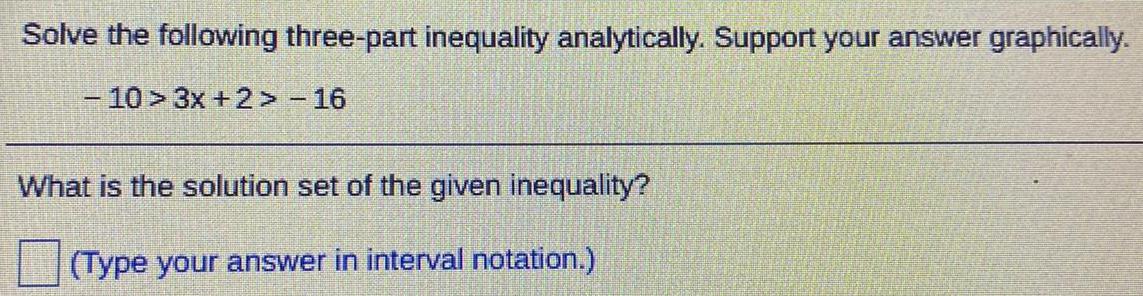
Math
Sets and RelationsSolve the following three-part inequality analytically. Support your answer graphically.
-10 > 3x +2> -16
What is the solution set of the given inequality?
Math
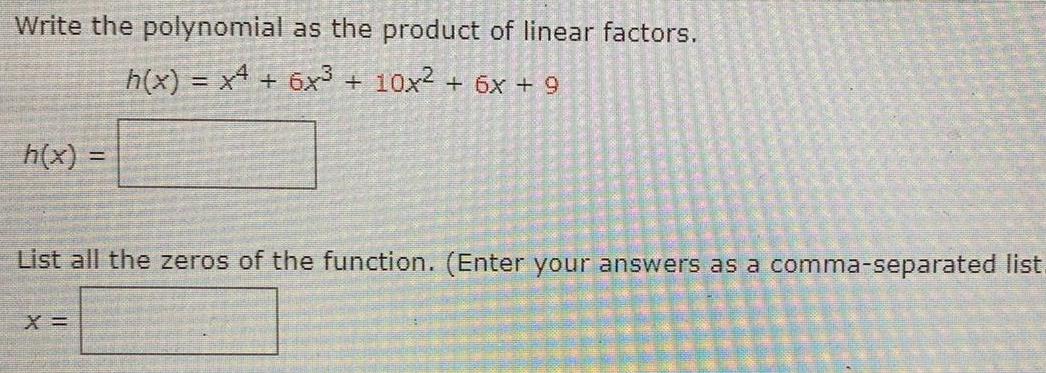
Sets and RelationsWrite the polynomial as the product of linear factors.
h(x) = x^4 + 6(x^3) + 10x² + 6x + 9
h(x)
List all the zeros of the function. (Enter your answers as a comma-separated list.
X =

Math
Sets and RelationsIn a group of 110 students, 65 play football, 45 play hockey, 42 curl, 20 play football and hockey, 25 play football and curling, 7 play hockey and curling but not football, and 8 play all the three games. Determine the number of students that don't play any of these sports.

Math
Sets and RelationsWhen cleaning out toys in her house, Mrs. Mulock is donating toys to Good Will. If 12 of them were educational toys, 10 are electronic toys, and 5 of them were both educational and electronic. What is the minimum number of toys she donated? Why is this a minimum?

Math
Sets and RelationsIs the following a power function, a polynomial, both, or neither?
f(x) = -5x² + 3x +3
Select the correct answer below:
Power function
Polynomial function
Both Power and Polynomial
Neither Power nor Polynomial
Math
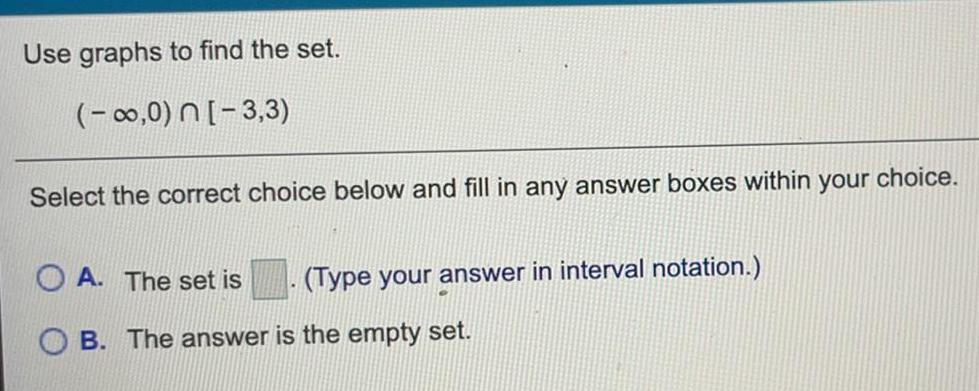
Sets and RelationsUse graphs to find the set.
(-∞,0) n[-3,3)
Select the correct choice below and fill in any answer boxes within your choice.
A. The set is
B. The answer is the empty set.
(Type your answer in interval notation.)

Math
Sets and RelationsSolve the quadratic equation by completing the square.
x²-14x-2=0
To complete the square, what number should be added to both sides of the equation?

Math
Sets and RelationsUse analytical and/or graphical methods to determine the intervals on which the following function has an inverse. (Make each interval as large as possible.)
f(x) = 1/x+6

Math
Sets and RelationsDetermine whether the relation represents a function. If this is a function, state the domain and range. Yes, Decause eacn element in the secona set corresponas to exacuy one element in the first set Select the list that represents the elements of the domain.
85%, 80%, 90%, 76%
90%, 76%, A, C
85%, 80%, 90%, 76%, B, A, C
This is not a function.
Select the list that represents the elements of the range.
www
Math
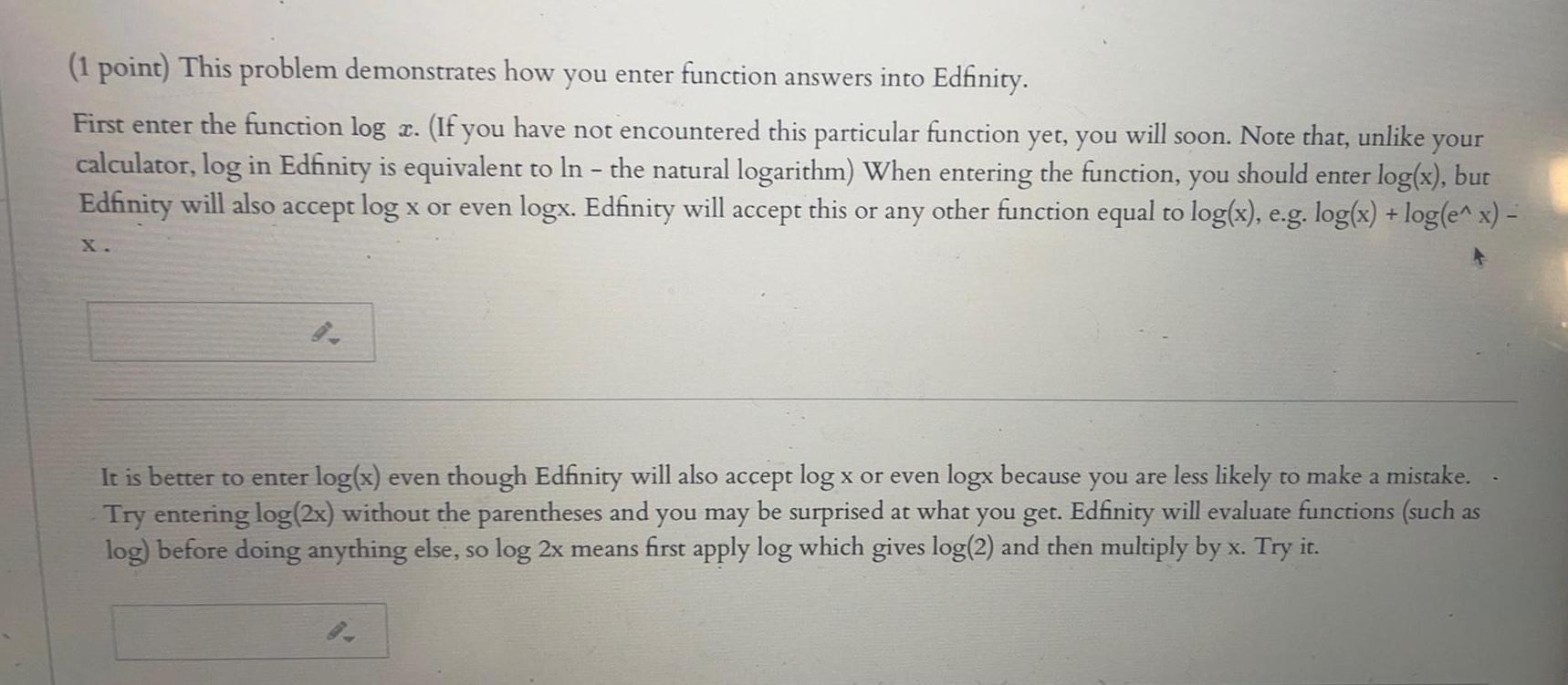
Sets and RelationsThis problem demonstrates how you enter function answers into Edfinity. First enter the function log æ. (If you have not encountered this particular function yet, you will soon. Note that, unlike calculator, log in Edfinity is equivalent to In - the natural logarithm) When entering the function, you should enter log(x), but Edfinity will also accept log x or even logx. Edfinity will accept this or any other function equal to log(x), e.g. log(x) + log(e^x) - It is better to enter log(x) even though Edfinity will also accept log x or even logx because you are less likely to make a mistake. Try entering log(2x) without the parentheses and you may be surprised at what you get. Edfinity will evaluate functions (such as log) before doing anything else, so log 2x means first apply log which gives log(2) and then multiply by x. Try it.

Math
Sets and RelationsI am looking for a function f define on R
I have shown that this function checks:
With f-1 (x) the inverse of f
am I allowed to say that f (x) = x + c? If so how do I show it (edited)

Math
Sets and RelationsBrenda has $500 in her bank account. Every week she withdraws $40 for
expenses. Gary has $800 in his account and every week withdraws $120. Without
making any more deposits, after how many weeks will Brenda have at least as much
money as Gary? Set up an equation and solve for the number of weeks.
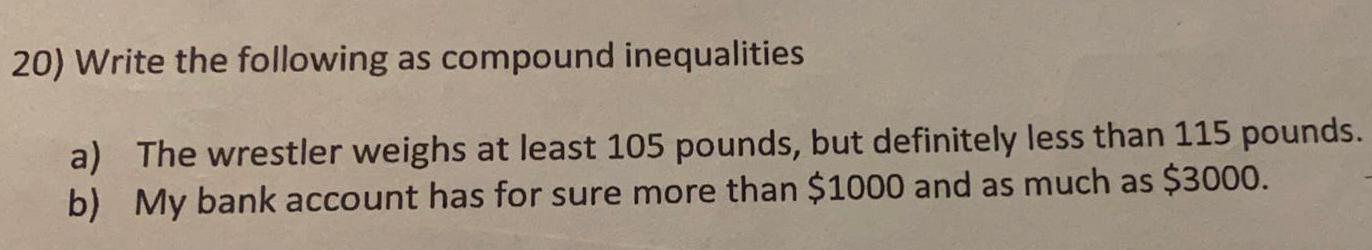
Math
Sets and RelationsWrite the following as compound inequalities
a) The wrestler weighs at least 105 pounds, but definitely less than 115 pounds.
b) My bank account has for sure more than $1000 and as much as $3000.

Math
Sets and RelationsIn 2003, the population of an African country was about 11.2 million people, which is 2 million more than 4 times the population in 1950. Enter and solve an equation to find the approximate population p (in millions) in 1950. An equation is The approximate population in 1950 was million people.

Math
Sets and RelationsA=(8, 8, 8, 9, 9, 10, 11, 12)
B=(12, 11, 10, 9, 8)
a. Are the sets equivalent? Explain.
A. The sets are equivalent because n(A) = n(B).
B. The sets are equivalent because set A does not contain the exact same elements as set B.
C. The sets are not equivalent because n(A) * n(B).
D. The sets are not equivalent because set A does not contain the exact same elements as set B.
b. Are the sets equal? Explain.
A. The sets are not equal because set A contains the exact same elements as set B.
B. The sets are equal because n(A) = n(B).
C. The sets are equal because set A contains the exact same elements as set B.
D. The sets are not equal because n(A) = n(B).

Math
Sets and RelationsList all the subsets of the given set.
{pineapple, orange, lemon}
Choose the answer that lists all of the subsets of (pineapple, orange, lemon}.
A. }, {pineapple}, {orange}, {lemon}, {pineapple, orange),
{pineapple, lemon}, {orange, lemon}
B. {pineapple}, {orange}, {lemon}, {pineapple, orange),
{pineapple, lemon}, {orange, lemon}
C. {pineapple}, {orange}, {lemon}, {pineapple, orange},
{pineapple, lemon}, {orange, lemon},
{pineapple, orange, lemon}
D. {}, {pineapple}, {orange}, {lemon}, {pineapple, orange},
{pineapple, lemon}, {orange, lemon},
{pineapple, orange, lemon}

Math
Sets and RelationsGiven the following sets, find the set An (BUC').
U= (1, 2, 3.....10)
A=(2, 3, 5, 9)
B=(1, 2, 3)
C = {1, 2, 3, 4, 5)
Select the correct choice below and, if necessary, fill in
A. An (BUC) - O
(Use a comma to separate answers as needed. U
A'n (BUC) is the empty set.
OB.
![[SolveLancer Test] The ratio of number of one-one function to number of constant
function for f: A → B where A = {3,8,9,10} and B = {11,12,14,15,20} is?
[SolveLancer Test]
(a) 20:1
(b) 25:1
(c) 24: 1
(d) 30:1](https://media.kunduz.com/media/sug-question/raw/54190927-1658000624.633805.jpeg?w=256)
Math
Sets and Relations[SolveLancer Test] The ratio of number of one-one function to number of constant
function for f: A → B where A = {3,8,9,10} and B = {11,12,14,15,20} is?
[SolveLancer Test]
(a) 20:1
(b) 25:1
(c) 24: 1
(d) 30:1

Math
Sets and RelationsWhat is the range of the polynomial function f(x) = x² - 2x³ + x −1?
O (-1.25,00)
O [-0.688,00)
O All real numbers.
o [-1.25,00)

Math
Sets and RelationsA survey of 84 college students was taken to determine the musical styles they liked. Of those, 34 students listened to rock, 36 to classical, and 34 to jazz. Also, 15 students listened to rock a
jazz, 20 to rock and classical, and 18 to classical and jazz. Finally, 10 students listened to all three musical styles. Construct a Venn diagram and determine the cardinality for each region. Use the completed Venn Diagram to answer the following questions.
a. How many listened to only rock music?
n(only rock)=
b. How many listened to classical and jazz, but not rock?
n(classical and jazz, not rock) =
c. How many listened to classical or jazz, but not rock?
n(classical or jazz, not rock) =
d. How many listened to music in exactly one of the musical styles?
n(exactly one style) =
e. How many listened to music in exactly two of the musical styles?
n(exactly two styles) =
f. How many did not listen to any of the musical styles?

Math
Sets and RelationsAnswer the following questions about the given sets.
a. Are the sets equivalent? Explain.
b. Are the sets equal? Explain.
A = (x | XEN and 103 ≤x≤ 108)
B = {x|XEN and 102<x< 109)
a. Are the sets equivalent? Explain.
A. The sets are not equivalent because n(A) = n(B).
B. The sets are equivalent because set A does not contain the exact same elements as set B.
C. The sets are not equivalent because set A does not contain the exact same elements as set B.
D. The sets are equivalent because n(A) = n(B).
b. Are the sets equal? Explain.
A. The sets are equal because n(A) = n(B).
B. The sets are equal because set A contains the exact same elements as set B.
C. The sets are not equal because n(A) = n(B).
D. The sets are not equal because set A contains the exact same elements as set B.
Math
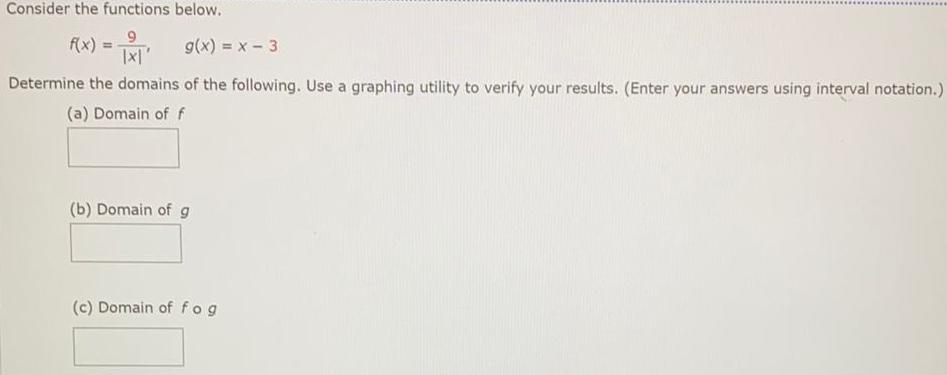
Sets and RelationsConsider the functions below.
f(x): 9 / |x|', g(x) = x - 3
Determine the domains of the following. Use a graphing utility to verify your results. (Enter your answers using interval notation.)
(a) Domain of f
(b) Domain of g
(c) Domain of f.g

Math
Sets and RelationsA study of 811 senior citizens shows that participants who exercise regularly exhibit less of a decline in the cognitive ability than those who barely exercise at all From
this study, a researcher infers that your cognitive ability increases the more you exercise. What is wrong with this type of reasoning?
The inference may incorrectly imply that exercise decreases a person's cognitive ability. The study shows an increase
in cognitive ability

Math
Sets and RelationsFind the domain and range of the relation. (b) Determine whether the relation is a function.
{(16,2), (2,7), (11,13), (13,13)}

Math
Sets and RelationsUse set notation to denote the elements, subsets, and complements of the following given sets.
N is the set of odd natural numbers greater than 11 and less than 21. Use set notation to write the elements of N.
N= {13, 15, 17, 19}
N= {12, 14, 16, 18, 20}
N= {11, 12, 14, 16, 18, 20, 21}
N= {11, 13, 15, 17, 19, 21}

Math
Sets and RelationsAssume that each set of statements is true. Usa the Law of Detachment to write a true statement. If the Law of Detachment cannot be used, explain why.If you can play the piano, then you can play a musical instrument. Kiyo can play a musical instrument.

Math
Sets and RelationsWriting On a number line, between which two consecutive whole numbers would V381 be located?
A. 19 and 20
B. 20 and 21
C. 18 and 19
D. 21 and 22
Explain why it might be useful to approximate the value rather than use the exact value.
![Express the interval in set-builder notation and graph the interval on a number line.
(7,9]
Select the correct choice below and, if necessasry, fill in the answer box to complete your choice.
A. The solution set in set-builder notation is {x
B. The solution set is all real numbers.
C. There is no solution.](https://media.kunduz.com/media/sug-question/raw/53564179-1657947053.8469403.jpeg?w=256)
Math
Sets and RelationsExpress the interval in set-builder notation and graph the interval on a number line.
(7,9]
Select the correct choice below and, if necessasry, fill in the answer box to complete your choice.
A. The solution set in set-builder notation is {x
B. The solution set is all real numbers.
C. There is no solution.
![Use graphs to find the set.
(-6,6) U[-3,8]
Select the correct choice below and fill in any answer boxes within choice.
A. The set is
B. The answer is the empty set your](https://media.kunduz.com/media/sug-question/raw/53539975-1657946094.470849.jpeg?w=256)
Math
Sets and RelationsUse graphs to find the set.
(-6,6) U[-3,8]
Select the correct choice below and fill in any answer boxes within choice.
A. The set is
B. The answer is the empty set your

Math
Sets and RelationsGive the domain and range of the relation.
{(-5, 1), (-5, 3), (9, 9), (4, -4), (-1, -1)}
domain = {4, -4, -5, -1, 9}; range = {-4, 3, -1, 9, 1}
domain = {4, -5, -1, 9}; range = {-4, 3, -1, 9, 1}
domain = {4, 14, -5, -1, 9}; range = {-4, 3, -1, 9, 1}
domain = {-4, 3, -1, 9, 1}; range = {4, 4, -5, -1, 9}

Math
Sets and RelationsSet F is defined to be all females living in the state of Florida. Set T is defined to be all teachers in the state of Florida. Set D is defined to be all people
who hold a doctorate degree currently living in Florida. Which description represents the set of the complement of F∩(DUT)?
All living in Florida, who are teachers in Florida hold a doctorate degree.

Math
Sets and RelationsIn a memory experiment, Alice is able to memorize words at a rate given by m'(t)= -0.015t2 +0.6t. In the same memory experiment, Ben is able to memorize words
at the rate given by M' (t)= -0.006² +0.6t.
a) Who has the higher rate of memorization?
Math
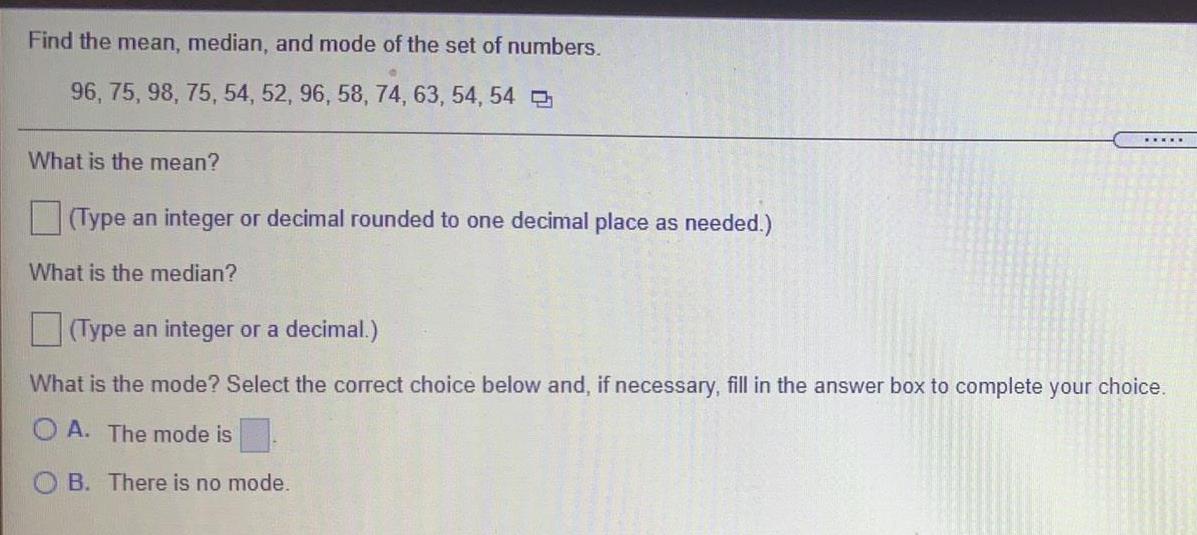
Sets and RelationsFind the mean, median, and mode of the set of numbers.
96, 75, 98, 75, 54, 52, 96, 58, 74, 63, 54, 54
What is the mean?
(Type an integer or decimal rounded to one decimal place as needed.)
What is the median?
*****
(Type an integer or a decimal.)
What is the mode? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The mode is
OB. There is no mode.

Math
Sets and RelationsJeremy is building a large deck for a community center. The deck is shaped as a rectangle. The width of the deck is 29 feet. The perimeter of the deck is to be at least 134 feet.
a. Write an inequality that represents all possible values for the length of the deck.
b. Solve algebraically to find all possible values for the length of the deck.

Math
Sets and RelationsA manufacturing company performs a quality-control analysis on the ceramic tile it produces. Suppose a batch of 20 tiles has 8 defective tiles. If 3 tiles are sampled at
random, what is the probability that exactly 1 of the sampled tiles is defective?
How many ways can 3 tiles be selected from 20 tiles?
ways
(Type a whole number.)
....
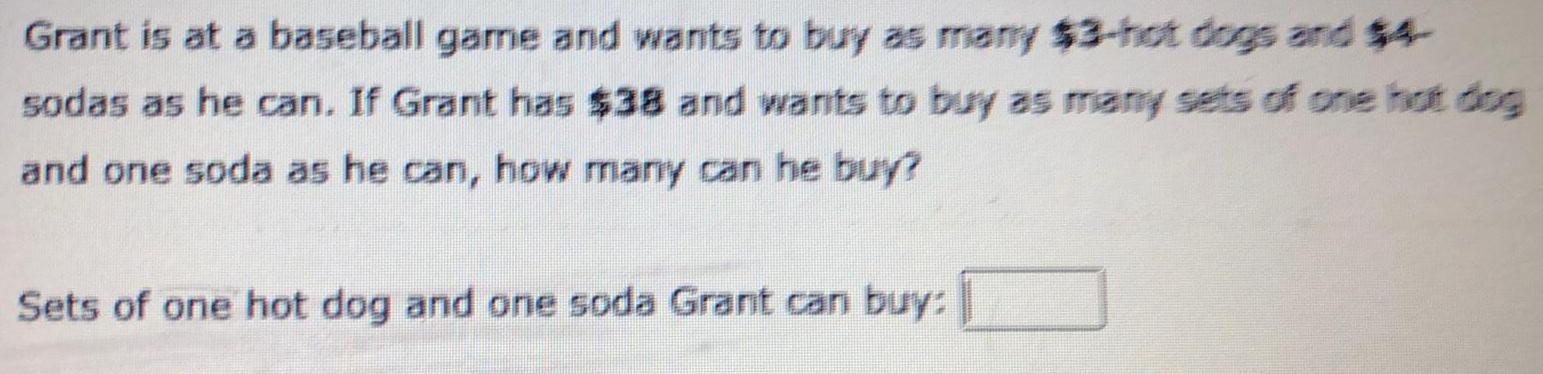
Math
Sets and RelationsGrant is at a baseball game and wants to buy as many $3-hot dogs and $4-
sodas as he can. If Grant has $38 and wants to buy as many sets of one hot dog
and one soda as he can, how many can he buy?
Sets of one hot dog and one soda Grant can buy:

Math
Sets and RelationsSuppose two dice (one red, one green) are rolled. Consider the following events: A: the red die shows 3; B: the numbers add to 5; C: at least one of the numbers is 2; and D: the numbers do not
add to 11. Express the given event in symbolic form.
The red die shows 3, but the numbers do not add to 11.
O AND
O AND'
O AUD
O AUD'
O AND
How many elements does it contain?
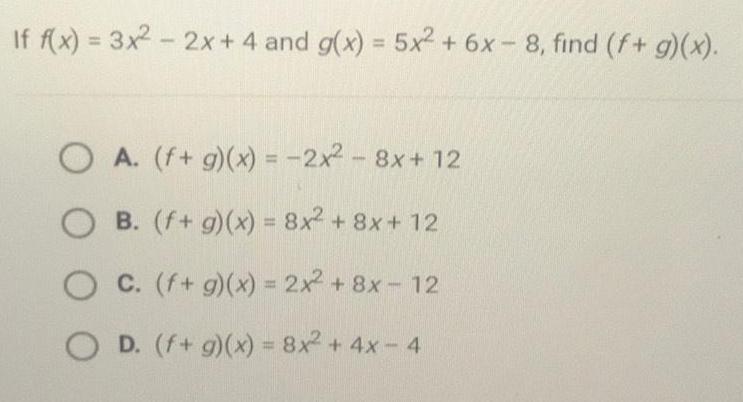
Math
Sets and RelationsIf f(x) = 3x² - 2x + 4 and g(x) = 5x² + 6x-8, find (f+ g)(x).
A. (f+ g)(x) = -2x² - 8x+12
B. (f+ g)(x) = 8x² + 8x + 12
C. (f+ g)(x) = 2x² + 8x - 12
D. (f+ g)(x) = 8x² + 4x - 4
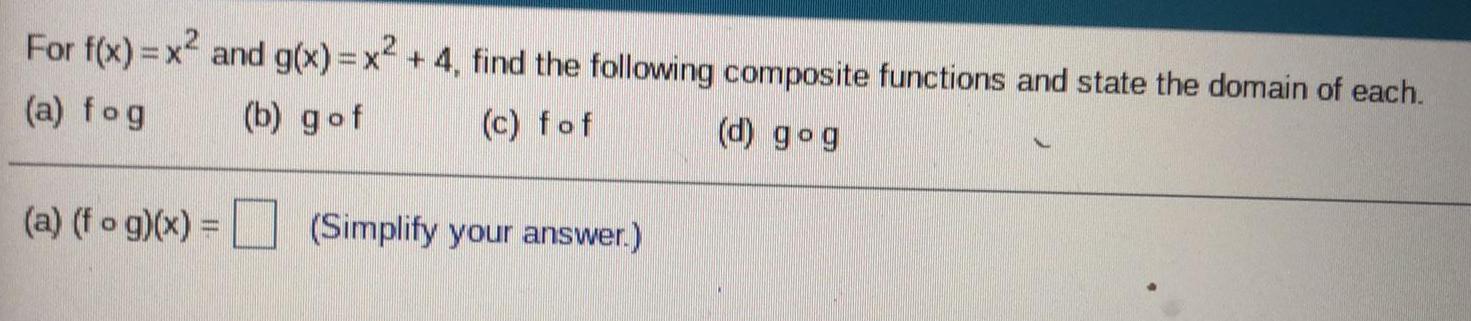
Math
Sets and RelationsFor f(x)=x² and g(x)=x² + 4, find the following composite functions and state the domain of each.
fog
gof
fof
gog
(fog)(x) = (Simplify your answer.)

Math
Sets and RelationsA middle school counselor, attempting to correlate school performance with leisure interests, found that of a group of students, 35 had seen Movie A, 29 had seen
Movie B, 26 had seen Movie C, 18 had seen Movies A and B, 13 had seen Movies A and C, 10 had seen Movies B and C, 5 had seen all three films, and 6 had seer
none of the three films. Use a Venn diagram to complete parts (a) through (c) below.
Complete the Venn diagram. Let A be the set of students that saw Movie A, B be the set of students that saw Movie B, and C be the set of students that saw Movie

Math
Sets and RelationsThe 69 students in a classical music lecture class were polled, with the results that 38 like Wolfgang Amadeus Mozart, 38 like Ludwig von Beethoven, 31 like Franz
oseph Haydn, 15 like Mozart and Beethoven, 20 like Mozart and Haydn, 14 like Beethoven and Haydn, and 8 like all three composers. Use a Venn diagram to
complete parts (a) through (f) below.
Complete the Venn diagram. Let M be the set of students that like Mozart, B be the set of students that like Beethoven, and H be the set of students that like Haydn.

Math
Sets and RelationsLet:
U={c, d, j, k, p, q, u}
X = {c, j. p, u}
Y = {c, d, j}
Z={d, j, k, p, q}
Find the following set:
(ZUX) NY


Math
Sets and RelationsLet A be the set A=(1,2,3,4) and let B be the set B=(5,6,7,8).
What is an element in B* A?