Trigonometry Questions and Answers

Math
TrigonometryJason sees a tall building from across town. He turns 90° and walks 100 yards. Jason then turns to face the building, and the angle between his line of sight and his path is 35° as shown below. Which of the following is the closest to the distance from Jason's original position to the building, in yards?

Math
TrigonometryGraph the function over a two-period interval. Give the period and amplitude.
y = 3 cos 2x
![What are the domain and range of the cosine function?
Domain: All Real Numbers
Range: (-1,1)
Domain: All Real Numbers
Range: [-1,1]
Domain: [-1,1]
Range: All Real Numbers
O Domain: All Real Numbers where ... -, 0, ...
Range: [-1,1]](https://media.kunduz.com/media/sug-question/raw/77197092-1660402142.635735.jpeg?w=256)
Math
TrigonometryWhat are the domain and range of the cosine function?
Domain: All Real Numbers
Range: (-1,1)
Domain: All Real Numbers
Range: [-1,1]
Domain: [-1,1]
Range: All Real Numbers
O Domain: All Real Numbers where ... -, 0, ...
Range: [-1,1]

Math
TrigonometryStudents were asked to prove the identity (sec x)(csc x) = cot x + tan x. Two students' work is given.
Student A
Step 1:
Step 2:
cos X sin x
Step 5:
1
cos x sin x
Step 4: cos²x
Step 3: cosx+sin²
cos x sin x
cos x sinx
COS X
sinx
11:
= cot x + tan x
cotx + tan x
X
cot x + tan x
sin² x
cos x sin x
sin x
COS X
11
cotx + tan x
Student B
Step 6: cot x + tan x = cot x + tan x
Step 1: secxcsc x =
Step 2: secxcscx =
cotx + tanx Step 4: secxcscx =
Step 3: secxcsc x =
cos x
sin x
Step 5: secxcsc x =
sinx
cos x
cos²x
cosxsin x
cos²x+sin² x
cos x sin x
1
cos x sinx
sin² x
cos xsin x
(x)(sinx)
Step 6: sec x csc X = sec x csc X
Part A: Did either student verify the identity properly? Explain why or why not. (10 points)
Part B: Name two identities that were used in Student A's verification and the steps they appear in. (5 poin

Math
TrigonometryWhy type of symmetry does the cosine function have?
Cosine is an odd function, meaning it has rotational symmetry about the origin.
Cosine is an even function, meaning it has symmetry with respect to the y axis.
Cosine is an odd function, meaning it has symmetry with respect to the y axis.
Cosine is an even function, meaning it has rotational symmetry about the origin.

Math
TrigonometryConsider the graph of f(x) = sin(x).
a. Describe the graph.
b. Can this graph be an example of any other function?
Hint (b):
c. Explain why f(x) = sin(x) cannot be a polynomial function.
Hint (c):


Math
TrigonometryShow that if is an integer multiple of 7, then sin(2x) = 2 sin(x).
Hint:
Graph the equations y = sin(2x) and y = 2-sin(x) on graphing paper or use Desmos calculator
Where are the two equations equal?
Use the Desmos calculator below to graph the equations.

Calculus
TrigonometryWhich of the following expressions could not be used to determine the exact value of cos 120°?
O cos^2(60°) - sin^2(60°)
O2cos^(60°) - 1
O 2sin(60°)cos(60°)
O 1 - 2sin^2(60°)

Calculus
TrigonometryGiven sin x=- 15/17 and cos x > 0, what is the exact solution of cos 2x?
O161/289
O225/289
O161/289
O225/289

Math
TrigonometryThe following problem refers to triangle ABC, find all missing parts. Round degrees to 1 decimal places and sides to the nearest whole number.
A = 21.6°, B = 51.4°, a = 130 inches
A =
B
C=
a= ___________ inches
b= ____________Inches
C=______________ inches

Math
TrigonometryFor the rotation 435°, find the coterminal angle from 0° 0 < 360°, the quadrant and the reference angle.
The coterminal angle is __° of which lies in Quadrant with a reference angle of ____°

Math
TrigonometryWhy type of symmetry does the sine function have?
Sine is an odd function, meaning it has symmetry with respect to the y axis.
Sine is an even function, meaning it has rotational symmetry about the origin.
Sine is an even function, meaning it has symmetry with respect to the y axis.
Sine is an odd function, meaning it has rotational symmetry about the origin.

Math
Trigonometrycos α =-24/25, α a lies in quadrant II, and sin B = √21, ß lies in quadrant II Find cos (α + β).
-48-7√21/125
14-24√21/125
-14+24/21/125
48+7√21/125
![What are the domain and range of the sine function?
Domain: All Real Numbers
Range: (-1,1)
Domain: All Real Numbers where x≠..... -π/2,π/2,....
Range: [-1,1]
Domain: [-1,1]
Range: All Real Numbers
Domain: All Real Numbers
Range: [-1,1]](https://media.kunduz.com/media/sug-question/raw/77081599-1660204481.981558.jpeg?w=256)
Math
TrigonometryWhat are the domain and range of the sine function?
Domain: All Real Numbers
Range: (-1,1)
Domain: All Real Numbers where x≠..... -π/2,π/2,....
Range: [-1,1]
Domain: [-1,1]
Range: All Real Numbers
Domain: All Real Numbers
Range: [-1,1]

Math
TrigonometryA farmer wants to build a new barn between her house and a pasture. She wants the ratio of the distance from the house to the barn and the barn to the pasture to be 7 to
1. She creates a map on a coordinate plane to represent her farm. She draws a point at (-20, 2) to represent her house and a point at (12, −6) to represent the pasture. At what point should she draw the point that represents the barn?
Enter the correct answer in the boxes.

Math
TrigonometrySuppose a right triangle contains an angle such that sin(θ) =3/7
Enter the exact values of the trig functions below:
cot (θ) = sin (θ) =
tan (θ) = cos(θ) =
csc (θ) = sec (θ)=

Math
TrigonometryWrite the expression cotθ cosθ tanθ cscθ using a single trigonometric function.
cos θ
sin θ
sec θ
cot θ

Algebra
Trigonometry7sin(3x) = 4 for the two smallest positive solutions A and B, with A<B
A =
B=
Give your answers accurate to at least two decimal places.

Math
Trigonometry7π/6 in degrees is _____________ degrees
The exact form of tan (7π/6) is ___________

Math
TrigonometryDetermine two coterminal angles (one positive and one negative) for each angle. Give your answers in radians. (Enter your answers as a comma-separated list.)
(a) 2π/3
(b) -9π/4

Math
TrigonometryA simple graph G on n vertices (n ≥ 2) is drawn in the plane. Prove that if every edge crosses at most one another edge, then the number of edges in G does not exceed 4n-8.

Math
TrigonometryIf the terminal side of angle θ, in standard position, passes through the point (-3, 4), what is the value of sin θ ?
(A) -5/4
(B) -3/4
(C) 4/5
(D) 4/3

Math
TrigonometryUse a half angle formula or formula for reducing powers to fill in the blanks in the identity below:
(cos(3x))² = _____ + ____ cos(_____ x)

Math
TrigonometryAccording to a Chinese legend from the Han dynasty (206 B.C.E.-220 C.E.), General Han Xin flew a kite over the palace of his enemy to determine the distance between his troops and the palace. If the general let out 800 meters of string and the kite was flying at a 35° angle of elevation, how far away was the palace from General Han Xin's position?

Math
TrigonometryFind all solutions of the equation. Express the solutions in radians in the form a + 2π, where a is in [0,2π). sin x = -√3 / 2

Math
TrigonometryFind the values of the trigonometric functions of from the information given. tan (θ)=12/5, θ in Quadrant III
sin(θ) =
cos(θ) =
csc(θ) =
sec(θ) =
cot(θ) =


Math
TrigonometryState the equation of the rational function if the vertical asymptote is x=5, the horizontal asymptote is y=2, and the x-intercept is -(1/2)
a) f(x) = 4x-1/2x-5
b) f(x)=2x+1/2x-10
c) f(x)=2x+1/2/x-5
d) f(x) = 2x+1/x-5

Math
TrigonometryThe slope of the tangent to the curve f(x) =2^x at x =1 is approximately (to three decimal places):
a) 1
b) 0.347
c) 0.693
d) 1.388

Math
TrigonometrySolve 3 cos²(x) + 5 cos(x) - 2 = 0 for the interval 0≤x≤ 2π
a) 1.231 and 5.052
b) 1.231
c) 1.231, 2.356, 2.759 and 5.052
d) 5.052

Math
TrigonometrySince the relationship sin²(x) + cos²(x) = 1 is correct, it stands to reason that sec²(x) + csc²(x) = 1 must also be correct. This statement is:
a) True for all values of x
b) Never true
c) True for the interval 0 ≤ x ≤ 2π
d) Not true only for the interval 0 ≤ x ≤ 2π

Math
TrigonometryWhich of the following is equivalent to:
tan (θ)/cos (θ)
a) cos(θ)/cot (θ)
b) csc(θ)/sin (θ)
c) 1
d) sec (θ)/cot (θ)

Math
TrigonometryAlthough 330° is a special angle on the unit circle, Amar wanted to determine its coordinates using the sum and difference formulas.
Part A: Determine cos 330° using the cosine sum identity. Be sure to include all necessary work. (5 points)
Part B: Determine sin 330° using the sine difference identity. Be sure to include all necessary work. (5 points)

Math
TrigonometryWhich expression is equivalent to tan(x) + cot(x)?
cos x/sec x
cos(x) sin(x)
1/sin(x) cos(x)
2 tan(x)

Math
TrigonometrySolve the equation on the interval [0, 2TT).
cos x - 2 cos x sin x = 0
π/6,5π/6
π/6,π/2,5π/6,3π/2
π/6,5π/6,2π
0,π/6,5π/6,3π/2

Math
TrigonometryTo further justify the Cofunction Thebrem, use your calculator to find a value for the given pair of trigonometric functions. The trigonometric functions are cofunctions of
complementary angles. Round each answer to four places past the decimal point.
sin 14°, cos 76⁰
sin 14° =
cos 76⁰ =

Math
TrigonometryFill in the blank to correctly complete the sentence.
For the polar equation r= 6 sin 40, if 0= 15°, then r =
For the polar equation r=6 sin 40, if 0=15°, then r =
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)

Math
TrigonometryConsider the trigonometric equation 2 sin(0) + 3 = 4, where the angle is measured in degrees.
One set of solutions is θ=
Another unique set of solutions is θ=

Math
TrigonometryConsidering only the values of ß for which sin ß tan ß sec ß cot ß is defined, which of the following expressions is equivalent to sin ß tan ß sec ß cot ß?
Select the correct answer below:
sec ß cot β
tan β
cot tan β
tan ß csc ß sec ß

Math
TrigonometryUse identities to find values of the sine and cosine functions for the angle measure.
θ, given that cos2θ= and 90° < θ < 180
sinθ =
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression. Rationalize all denominators.)
cosθ=
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression. Rationalize all denominators.)

Math
TrigonometryGiven: cos (4π/9) cos(2π/9) — sin (4π/9) sin(2π/9) 1. Identify the Trig identity that corresponds with the expression above. 2. Simplify and find the exact value. Show all work. Answers without justification will

Math
TrigonometryA building 29.94 feet tall has a shadow that is 33.11 feet long. Find the angle of elevation of the sun to the nearest hundredth of a degree.
The angle of elevation is degrees.
(Round to the nearest hundredth as needed.)

Math
TrigonometryFrom the observation deck of a skyscraper, Meena measures a 45° angle of depression to a ship in the harbor below. If the observation deck is 862 feet high, what is the horizontal distance from the base of the skyscraper out to the ship? Round your answer to the nearest tenth of a foot if necessary.

Math
TrigonometryInformation about △ABC is given.
Determine all remaining information about the triangle. Answers must be accurate to three decimal places. If there are multiple triangles with the given information, determine all of them. If a triangle cannot be solved, explain why not.
a) A = 60°2 a = 52 b= 6
b) a = 3, b = 8, c = 50°
![Find the cosine of the angle between A and B with respect to the standard inner product on M22
A =[3 3] and B = [4 2]
[3 -1] [3 2]
Carry out all calculations exactly and round to 4 decimal places the final answer only](https://media.kunduz.com/media/sug-question/raw/77321865-1658837231.950191.jpeg?w=256)
Math
TrigonometryFind the cosine of the angle between A and B with respect to the standard inner product on M22
A =[3 3] and B = [4 2]
[3 -1] [3 2]
Carry out all calculations exactly and round to 4 decimal places the final answer only

Math
TrigonometryThe point P(x, y) on the unit circle that corresponds to a real number t is given. Find the value of the indicated trigonometric function at t.
(3/4, √7/4) Find sin t.
A) 3/4
B) 3√7/7
C) √7/3
D) √7/4
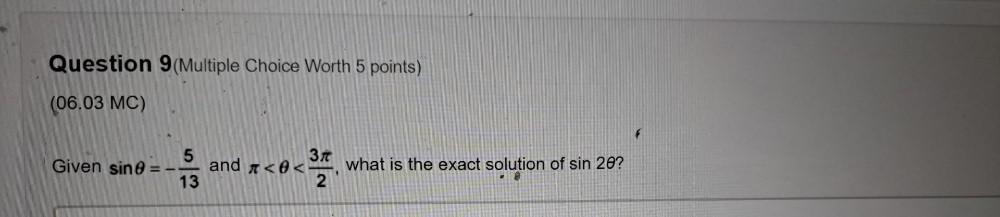


Math
TrigonometryFind the exact value of the expression: cos(165°)
The final solution needs to be simplified for full credit.