Application of derivatives Questions and Answers

Math
Application of derivativesGravel is being dumped from a conveyor belt at a rate of 20 ft³/min. It forms a pile in the shape of a right circular cone whose base diameter and height are always the same How fast is the height of the pile increasing when the pile is 21 ft high? The height is increasing at t/min

Math
Application of derivativesLet f(x)=x-7/2x+6
Find an equation for the tangent line to the graph of f at x = 3.
Tangent line: y =

Math
Application of derivativesConsider the following vector function.
r(t) = (7t2, sin(t)- t cos(t), cos(t) + t sin(t)), t> 0
(a) Find the unit tangent and unit normal vectors T(t) and N(t).
T(t) =
N(t) =
(b) Use this formula to find the curvature.
k(t) =

Math
Application of derivativesA cylinder shaped can needs to be constructed to hold 450 cubic centimeters of soup. The material for the sides of the can costs 0.02 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.06 cents per square centimeter. Find the dimensions for the can that will minimize production cost.
Helpful information:
h: height of can, r: radius of can
Volume of a cylinder: V = π²h
Area of the sides: A=2πrh
Area of the top/bottom: A=πr²
To minimize the cost of the can:
Radius of the can:
Height of the can:
Minimum cost: cents
Math
Application of derivativesA baseball diamond is a square with sides of length 90 ft. A batter hits the ball and runs toward first base with a speed of 22 ft/s.
At what rate is his distance from second base changing when he is halfway to first base?
Answer= ft/s
At what rate is his distance from third base changing at the same moment?
Answer=ft/s

Math
Application of derivativesIf an arrow is shot straight upward on the moon with a velocity of 72 m/s, its height (in meters) after t seconds is given by s(t) = 72t - 0.83t²
What is the velocity of the arrow (include units) after 8 seconds?
How long will it take for the arrow to return and hit the moon (include units)?
With what velocity (include units) will the arrow hit the moon?

Math
Application of derivativesA road perpendicular to a highway leads to a farmhouse located 2 mile away. An automobile traveling on the highway passes through this intersection at a speed of 55mph. How fast is the distance between the automobile and the farmhouse increasing when the automobile is 2 miles past the intersection of the highway and the road?
The distance between the automobile and the farmhouse is increasing at a rate of ______miles per hour

Math
Application of derivativesA 16 ft ladder leans against a wall. The bottom of the ladder is 3 ft from the wall at time t = 0 and slides away from the wall at a rate of 3ft/sec Find the velocity of the top of the ladder at time t = 2

Math
Application of derivativesThe minute hand on a watch is 8 mm long and the hour hand is 4 mm long How fast is the distance between the tips of the hands changing at one o'clock? Round your answer to the nearest tent

Math
Application of derivativesA water trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm If the trough is being filled with water at a rate of 2 m³/min, how fast is the water level rising when the water is 30 cm deep?

Math
Application of derivativesUse an appropriate local linear approximation to estimate the value of the given quantity.
(2.04)3
Math
Application of derivativesA silver bar with a specific heat of 0.235 J/g°C has a mass of 250. g and is heated from 22.0°C to 68.5°C. How much heat will the silver bar absorb?
a) 4020 J
b) 5320 J
c) 49,500 J
d) 2730 J

Math
Application of derivativesA cylinder shaped can needs to be constructed to hold 300 cubic centimeters of soup. The material for the sides of the can costs 0.03 cents per square centimeter. The material for the top and bottom of the can need to be thicker, and costs 0.05 cents per square centimeter. Find the dimensions for the can that will minimize production cost.

Math
Application of derivatives(A) Find the average rate of change of the area of a circle with respect to its radius r as r changes from
(i) 5 to 6 →→ Average rate of change =
(ii) 5 to 5.4 → Average rate of change =
(iii) 5 to 5.1 → Average rate of change =
(B) Find the instantaneous rate of change when r = 5.
Instantaneous rate of change =
![A box with a square base and open top must have a volume of 48668 cm³. We wish to find the dimensions of the box that minimize the amount of material used.
First, find a formula for the surface area of the box in terms of only a, the length of one side of the square base.
[Hint: use the volume formula to express the height of the box in terms of x.]
Simplify your formula as much as possible.
A(x) =
Next, find the derivative, A'(x).
A'(x) =
Now, calculate when the derivative equals zero, that is, when A'(x) = 0. [Hint: multiply both sides by x².]
A'(x) = 0 when x =
We next have to make sure that this value of a gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x).
A"(x)=
Evaluate A"(x) at the x-value you gave above.
NOTE: Since your last answer is positive, this means that the graph of A(x) is concave up around that value, so the zero of A'(x) must indicate a local minimum for A(x). (Your boss is happy now.)](https://media.kunduz.com/media/sug-question/raw/47858147-1658333755.3716078.jpeg?w=256)
Math
Application of derivativesA box with a square base and open top must have a volume of 48668 cm³. We wish to find the dimensions of the box that minimize the amount of material used.
First, find a formula for the surface area of the box in terms of only a, the length of one side of the square base.
[Hint: use the volume formula to express the height of the box in terms of x.]
Simplify your formula as much as possible.
A(x) =
Next, find the derivative, A'(x).
A'(x) =
Now, calculate when the derivative equals zero, that is, when A'(x) = 0. [Hint: multiply both sides by x².]
A'(x) = 0 when x =
We next have to make sure that this value of a gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x).
A"(x)=
Evaluate A"(x) at the x-value you gave above.
NOTE: Since your last answer is positive, this means that the graph of A(x) is concave up around that value, so the zero of A'(x) must indicate a local minimum for A(x). (Your boss is happy now.)
Math
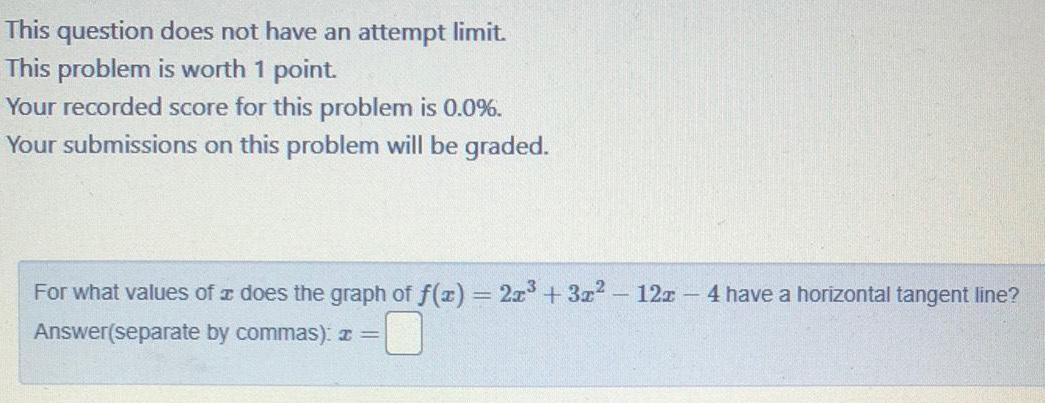
Application of derivativesFor what values of a does the graph of f(x) = 2x³ + 3x² - 12z - 4 have a horizontal tangent line?
Answer(separate by commas): x =

Math
Application of derivativesFind the rate of increase (with respect to r) in the surface area (S = 47²) of a spherical balloon when:
(A) r = 1 inches → Rate of increase =
(B) r = 4 inches → Rate of increase =
(C) r = 5 inches →
Rate of increase =

Math
Application of derivativesSuppose that 108 ft of fencing are used to enclose a corral in the shape of a rectangle with a semicircle whose diameter is a side of the rectangle as the following figure: Find the dimensions of the corral with maximum area.

Math
Application of derivativesUse differentials to estimate the amount of paint needed to apply a coat of paint .05 cm thick to a hemispherical dome with diameter 50 m.

Math
Application of derivativesA spotlight on the ground is shining on a wall 12m away. If a woman 2 tall walks from the spotlight toward the building at a speed of 0.8m/s, how fast is the length of her shadow on the building decreasing when she is 4m from the building?

Math
Application of derivativesA 15 Rt ladder leans against a wall. The bottom of the ladder is 5 ft from the wall at time t= 0 and slides away from the wall at a rate of 2ft/sec Find the velocity of the top of the ladder at time t = 1.

Math
Application of derivativesA potter forms a piece of clay into a right circular cylinder. As she rolls it, the height h of the cylinder increases and the radius r decreases. Assume that no clay is lost in the process. Suppose the height of the cylinder is increasing by 0.6 centimeters per second. What is the rate at which the radius is changing when the radius is 7 centimeters and the height is 11 centimeters?

Math
Application of derivativesIf f(x) = 4x² - 2x + 4 then:
ƒ'(2)=
An equation for the line tangent to y = f(x) at the point where x =
y =

Math
Application of derivativesAn equation for the line tangent to the graph of f(x) = 5x - 3+ 9ex at the point where x = - 5:
y =

Math
Application of derivativesGiven the function g(x) = 6x³ +54x² + 90x, find the first derivative, g'(x).
g'(x) =
Notice that g'(x) 0 when a = 5, that is, g'(-5) = 0.
Now, we want to know whether there is a local minimum or local maximum at x = -5, so we will use the second derivative test.
Find the second derivative, g''(x).
g''(x) =
Evaluate g''(-5).
g''(-5) =
Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at
x = -5?
At x = -5 the graph of g(x) is
Based on the concavity of g(x) at x =-5, does this mean that there is a local minimum or local maximum
at x = -5?
At x = - 5 there is a local

Math
Application of derivativesSuppose that a certain radioactive element has an annual decay rate of 8%. Starting with a 4,329 gram sample of the element, how many grams will be left in 10 years? Round your answer to the nearest gram.

Math
Application of derivativesThis function:
f(x)=- 40x4e-x
has critical numbers:
On the graph of y = f(x) the smallest critical number
corresponds to:
a local maximum
a local minimum
neither a local maximum or a local minimum
On the graph of y = f(x) the largest critical number
corresponds to:
a local maximum
a local minimum
neither a local maximum or a local minimum

Math
Application of derivativesA company sells tires and rents out a portion of its warehouse to
another company for a fixed rent of $8,000. The accounting
department claims the company's monthly profit is determined by the
profit function: P(x) = x³ - 8x² + 16x + 8 in thousands
of dollars (already taking the rent into account).
What is the company's maximum profit during the first three months?

Math
Application of derivativesThe number of mosquitoes in Brooklyn (in millions of mosquitoes) as a function of rainfall (in centimeters) is modeled by
m(x) = -2(x-4)
What is the maximum possible number of mosquitoes?

Math
Application of derivatives8 A radioactive isotope is decaying at a rate of 18% every hour. Currently there are 100 grams of the substance.
Part B: How much will be left one day from now? Round your answer to the nearest hundredth.

Math
Application of derivativesUse Newton's method to approximate a root of the equation
3 sin(x) = x as follows.
Let x1 = 2 be the initial approximation.
The second approximation 2 is
and the third approximation is

Math
Application of derivativesUse Newton's Method to estimate a root of the function
f(x) = 5x + 2 - ex
Use the initial estimate x1 = 0.5:
x1 = 0.5
x2
x3
X4
X5 =
x6
X7

Math
Application of derivativesSuppose h" is continuous at x = 5.h' (5)= 0, and h" (5) > 0.
What can you say about the behavior of h at x = 5?
Inflection point
Inflection point at a horizontal tangent
Relative (local) maximum
Relative (local) minimum

Math
Application of derivativesThe function f(x) = 2x³ − 27x² +84x + 3 has one local minimum and one local maximum. Use a graph of the function to estimate these local extrema.
This function has a local minimum at x = ___ with output value ___ and a local maximum at x = ___ value with output ___

Math
Application of derivativesSuppose a hiker finds himself in a forest 3 miles from the nearest point on a straight road. He wants to walk to his car which is parked 10 miles down the road. He can walk 4 mph along the road, but only 2 miles per hour through the forest. Toward what point, in miles, on the road should he walk in order to reach his car in the least time? Note: Round to the nearest thousandth.

Math
Application of derivativesUse linear approximation, i.e. the tangent line, to approximate 1/0.103 as follows: Let f(x) = 1/x and find the equation of the tangent line to f(x) at a "nice" point near 0.103. Then use this to approximate 1/0.103.

Math
Application of derivativesSuppose h" is continuous at x = 2.h' (2) = 0, and h" (2) < 0.
What can you say about the behavior of h at x = 2?
Inflection point
Inflection point at a horizontal tangent
Relative (local) minimum
Relative (local) maximum
![Let f(x) = (3x - 1)² (3x - 7)² on [1,3]. Answer the following.
(a) Find all critical numbers of f.
(b) Find the intervals on which f is increasing.
(c) Find absolute extreme value of f.](https://media.kunduz.com/media/sug-question/raw/46196864-1658295031.8314972.jpeg?w=256)
Math
Application of derivativesLet f(x) = (3x - 1)² (3x - 7)² on [1,3]. Answer the following.
(a) Find all critical numbers of f.
(b) Find the intervals on which f is increasing.
(c) Find absolute extreme value of f.

Math
Application of derivativesA toy manufacturing company's monthly profit in its first two months of operation is given by the profit function
P(x) = x³ -6x2 +9x+6, where is the number of toys sold and P(x) is In thousands of dollars (for example, if P(x) = 3, then the company's profit is $3000).
What is the company's maximum profit during the first two months?

Math
Application of derivativesUse Newton's method to approximate a root of the equation
4x7 + 5x4 + 2 = 0 as follows.
Let x1=2 be the initial approximation.
The second approximation x2 is
and the third approximation x3 is
Carry at least 4 decimal places through your calculations.

Math
Application of derivativesA cube is expanding, with the length of an edge decreasing 2 cm every minute. At the moment the cube has a volume of 343 cm³, the rate at which the volume of the cube is changing is:

Math
Application of derivativesIf you have 240 meters of fencing and want to enclose a rectangular area up against a long, straight wall, what is the largest area you can enclose? Area = (include units)

Math
Application of derivativesA street light is at the top of a 15 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 5 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 30 ft from the base of the pole?

Math
Application of derivativesAn inverted pyramid is being filled with water at a constant rate of 60 cubic centimeters per second. The pyramid, at the top, has the shape of a square with sides of length 2 cm, and the height is 7 cm.
Find the rate at which the water level is rising when the water level is 5 cm. cm/sec

Math
Application of derivativesA circle is inside a square. The radius of the circle is decreasing at a rate of 3 meters per day and the sides of the square are increasing at a rate of 4 meters per day. When the radius is 3 meters, and the sides are 15 meters, then how fast is the AREA outside the circle but inside the square changing?

Math
Application of derivativesBetween two telephone poles that are 40 feet apart, there is a wire
suspended in the shape of a catenary y = 25 cosh (x/25) - 5, where
and y are measured in feet and -20 ≤ x ≤ 20.
What is the slope of the curve where the wire meets the right pole?
Note: Round to the nearest thousanth.

Math
Application of derivativesFermium-257 has a half-life of 100 days. A sample has a mass of 60 mg initially.
I) What is the formula for finding the amount remaining after t days.
II) When will there only be 5 mg remaining?
A) y = 60(2) -t 100; 248 days
B) y = 60 e -t 100; 248 days
C) y = 60(2) -t 100; 358 days
D) y = 60e -t 100; 358 days

Math
Application of derivativesFind the coordinates of the vertex of the graph of the function. Tell whether the vertex is a maximum or a minimum.
y = -2x² -12x - 6
(3,-60); minimum
(-3,48); maximum
(12,-3); minimum
(-3,12); maximum

Math
Application of derivativesBetween two telephone poles that are 44 feet apart, there is a wire suspended in the shape of a catenary y = 15 cosh (x/15) - 8, where x and y are measured in feet and
-22 ≤ x ≤ 22.
What is the slope of the curve where the wire meets the left pole?

Math
Application of derivativesAt noon, ship A is 40 nautical miles due west of ship B. Ship A is sailing west at 21 knots and ship B is sailing north at 24 knots. How fast (in knots) is the distance between the ships changing at 4 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)