Application of derivatives Questions and Answers
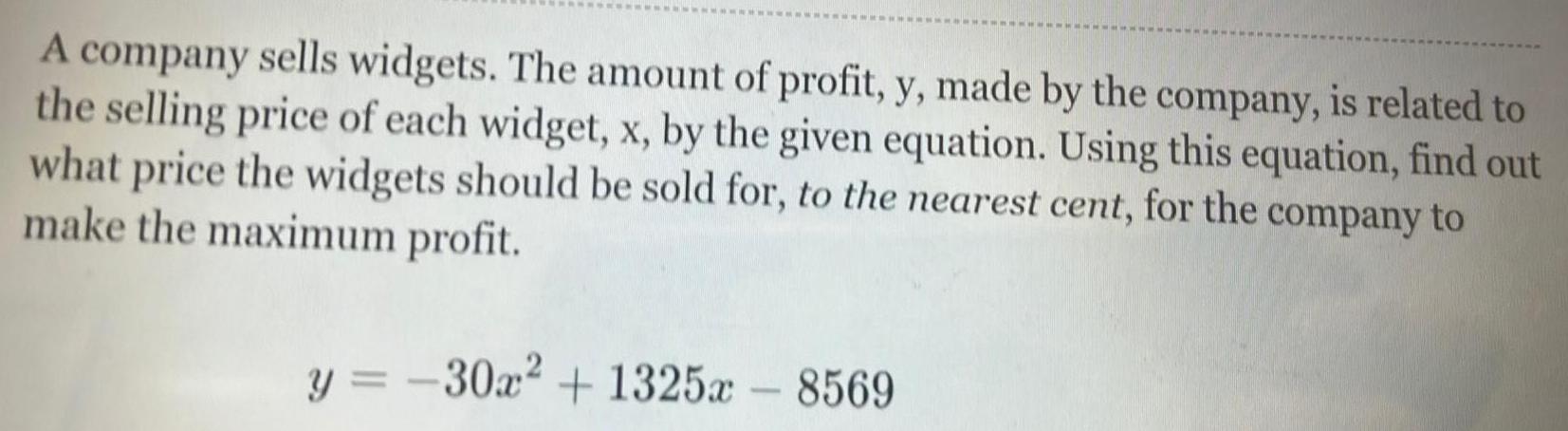
Math
Application of derivativesA company sells widgets. The amount of profit, y, made by the company, is related to
the selling price of each widget, x, by the given equation. Using this equation, find out
what price the widgets should be sold for, to the nearest cent, for the company to
make the maximum profit.
y = -30x² +1325x - 8569

Math
Application of derivativesThe percent of concentration of a certain drug in the bloodstream x hr after the drug
is administered is given by K(x) = How long after the drug has been 3x / x2 - 36
administered is the concentration a maximum? Round answer to the nearest tenth, if
necessary.
A) 3 hr
B) 3.6 hr
C) 6hr
D) 1.8 hr
Math
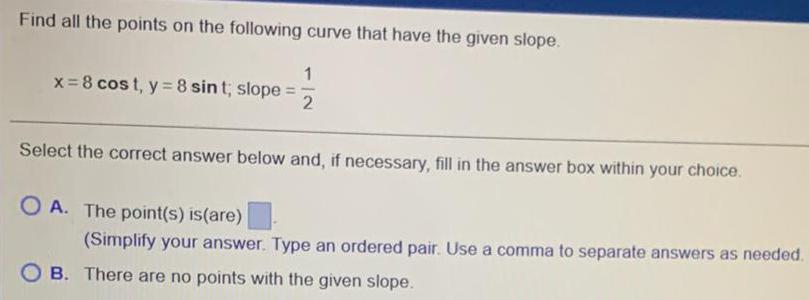
Application of derivativesFind all the points on the following curve that have the given slope.
x=8 cost, y = 8 sint; slope =1/2
Select the correct answer below and, if necessary, fill in the answer box within your choice.
A. The point(s) is(are)
(Simplify your answer. Type an ordered pair. Use a comma to separate answers as needed.
B. There are no points with the given slope.

Math
Application of derivativesThe function f(x) =
2x³ + 30x² - 144x +9 has one local minimum and one local maximum.
This function has a local minimum at x =
with value
and a local maximum at =
with value

Math
Application of derivativesThe amount of carbon-15 in a given sample decays exponentially with time. If the function C(m)=100(1/2)^24m models the amount of carbon remaining in the sample after m minutes, which the following must be true?
A) The amount of carbon in the sample halves ex minute.
B) The amount of carbon in the sample halves 24 minutes.
C) The amount of carbon in the sample halve 24 times every minute.
D) The amount of carbon in the sample redatel factor of 24 every 2 minutes,

Math
Application of derivativesFind the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.)
/ 7x5 +6/x² + 6x dx
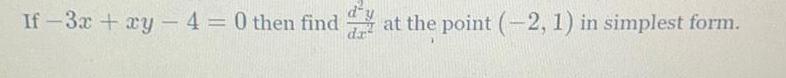
Math
Application of derivativesIf-3x + xy -4 = 0 then find d^2y / dx^2 at the point (-2,1) in simplest form.
![A stone is thrown vertically upward from a platform that is 16 feet above ground at a rate of 50 feet per second. Use the projectile formula h = - 16t² + vot + ho to find how long it will take the stone to reach its maximum height, and then find the maximum height the stone reaches. [Recall that vo is the initial velocity of the object and he is the inital height of the object.]
Answer: The stone reaches its maximum height after height the stone reaches is](https://media.kunduz.com/media/sug-question/raw/60871482-1657290252.9756644.jpeg?w=256)
Math
Application of derivativesA stone is thrown vertically upward from a platform that is 16 feet above ground at a rate of 50 feet per second. Use the projectile formula h = - 16t² + vot + ho to find how long it will take the stone to reach its maximum height, and then find the maximum height the stone reaches. [Recall that vo is the initial velocity of the object and he is the inital height of the object.]
Answer: The stone reaches its maximum height after height the stone reaches is

Math
Application of derivativesA spherical weather balloon is being inflated. The radius of the balloon is increasing at the rate of 5 cm/s. Express the surface area of the balloon as a function of time t (in seconds). (Let S(0) = 0.)
s(t) = cm²

Math
Application of derivativesA fence must be built to enclose a rectangular area of 5000 ft2. Fencing material costs $2 per foot for the two sides facing north and south and $4 per foot for the other two sides. Find the cost of the least expensive fence. The cost of the least expensive fence is $ .
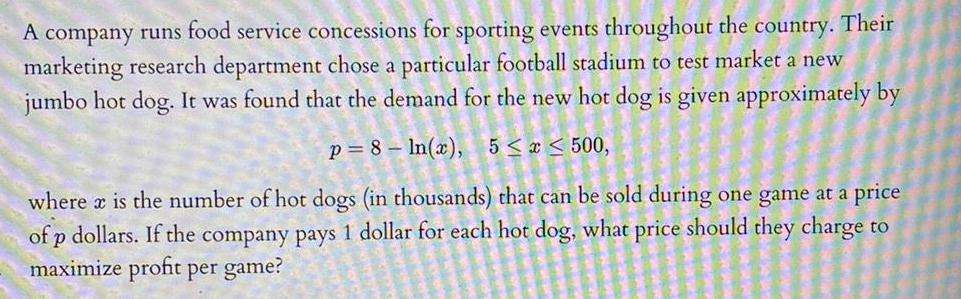
Math
Application of derivativesA company runs food service concessions for sporting events throughout the country. Their marketing research department chose a particular football stadium to test market a new jumbo hot dog. It was found that the demand for the new hot dog is given approximately by
p=8-In(x), 5 ≤ x ≤ 500,
where x is the number of hot dogs (in thousands) that can be sold during one game at a price of p dollars. If the company pays 1 dollar for each hot dog, what price should they charge to maximize profit per game?

Math
Application of derivativesA ball is thrown into the airfrom the roof of a 200 foot tall building with an initial upward velovity of 80 ft/sec. Its height function is given by h(t) = -16t² + 80t +200. What is the maximum height reached by the ball?
Math
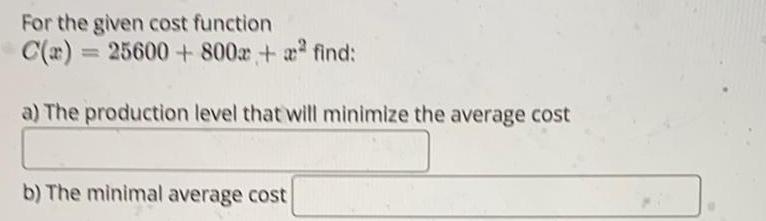
Application of derivativesFor the given cost function
C(x) = 25600 + 800x + x² find :
a) The production level that will minimize the average cost
b) The minimal average cost

Math
Application of derivativesKatie want to build a rectangular enclosure for your pet rabbit, Sniper, against the side of her house. She has bought 150 feet of fencing. What are the dimensions of the largest area that she can enclose?

Math
Application of derivativesWater flows into a hemispherical tank of radius 10
feet (flat side up). At any instant, let h denote the
depth of the water, measured from the bottom, r
the radius of the surface of the water, and V the
volume of the water is the tank. Compute dv/dh at
the instant when h=5 feet. If the water flows in at
a constant rate of 5√3 cubic feet per second,
compute dr/dt, the rate at which r is changing, at
the instant t when h = 5 feet.
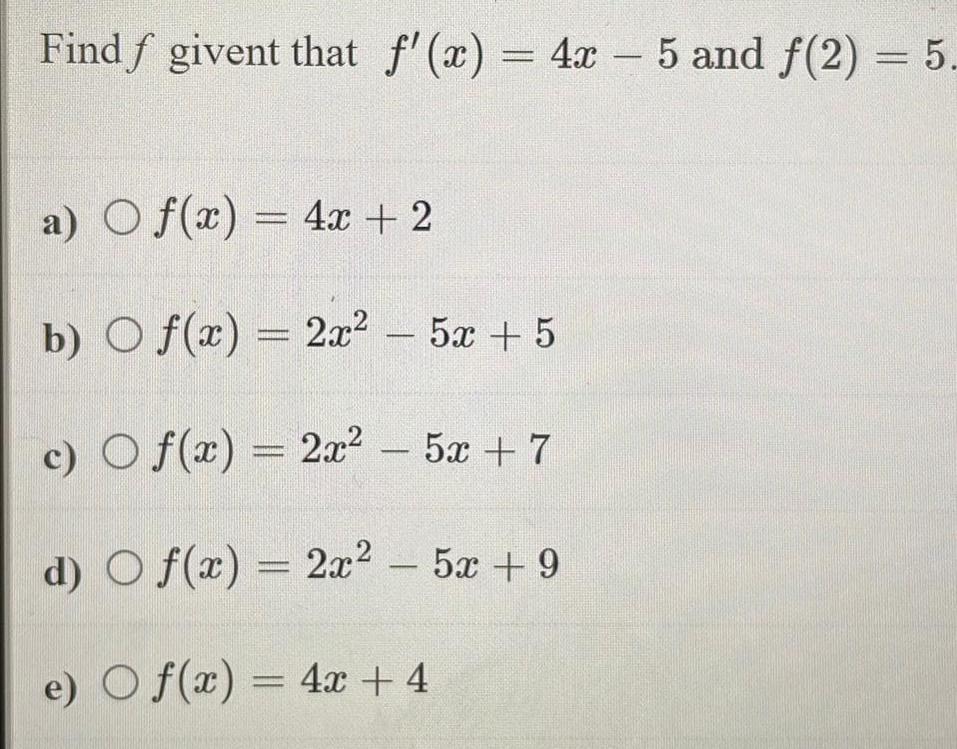
Math
Application of derivativesFind f givent that f'(x) = 4x - 5 and f(2) = 5.
a) f(x) = 4x + 2
b) f(x) = 2x² - 5x + 5
c) f(x) = 2x² 52+7
d) f(x) = 2x² - 5x +9
e) f(x) = 4x + 4

Math
Application of derivativesThe monthly average high temperatures in degrees Fahrenheit at a beach can be modeled by P(x) = 0.0143x4 -0.425x3 +3.545x2-6.256x+64, where x = 1 corresponds to January and x = 12 represents December.
(a) Find the average high temperature during March and August.
(b) Estimate graphically and numerically the months when the average high temperature is about 70°F.
(
a) Using the model P(x), the average high temperature in March is F. and the average high temperature in August is °F. (Type an integer or decimal rounded to the nearest tenth as needed.)

Math
Application of derivativesFor a certain automobile, M(x) = - .015x² +1.22x-7.8, 30 ≤x≤ 60, represents the miles per gallon obtained at a speed of x miles per hour
(a) Find the absolute maximum miles per gallon and the speed at which it occurs.
(b) Find the absolute minimum miles per gallon and the speed at which it occurs.
(a) The absolute maximum miles per gallon is .This occurs at mph.
(Type an integer or decimal rounded to the nearest thousandth as needed.)
Math
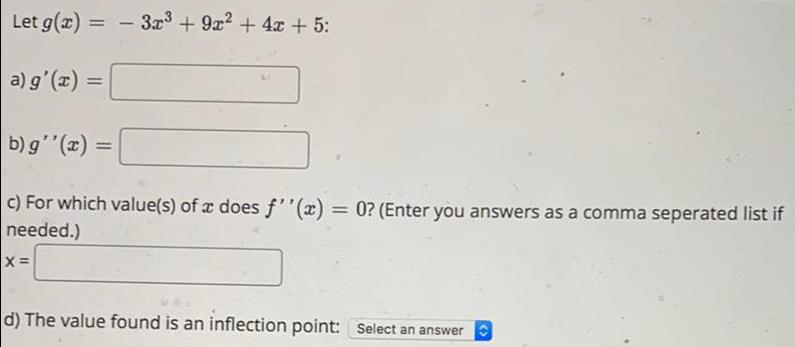
Application of derivativesLet g(x) = - 3x³ + 9x² + 4x + 5:
a) g'(x) =
b) g''(x) =
c) For which value(s) of a does f''(x) = 0? (Enter you answers as a comma seperated list if needed.)
X =
d) The value found is an inflection point: Select an answer

Math
Application of derivativesA county realty group estimates that the number of housing starts per year over the next three years will be H(r) = 200/ (1+0.03r²) where r is the mortgage rate (in percent).
(a) Where is H(r) increasing?
(b) Where is H(r) decreasing?

Math
Application of derivativesConsider the following parametric equations.
a. Eliminate the parameter to obtain an equation in x and y.
b. Describe the curve and indicate the positive orientation.
x=r-4, y=r³-1, -3≤r≤3
a. Eliminate the parameter to obtain an equation in x and y.
y+1=(x+4) (Type an equation.)
b. Describe the curve and indicate the positive orientation.
(Type ordered pairs. Simplify your answers.)
A. A cubic curve falls to the left as r increases, starting at and ending at
B. A quadratic curve falls and then rises to the left as r increases, starting at and ending at
C. A quadratic curve falls and then rises to the right as r increases, starting at and ending at
D. A cubic curve rises to the right as r increases, starting at and ending at

Math
Application of derivativesUse the derivative f'(x)= (x-3)(x + 1)(x + 4) to determine the local maxima and minima of f and the intervals of increase and decrease. Sketch a possible graph of f (f is not unique).
The local maximum/maxima is/are at x = (Use a comma to separate answers as needed.)

Math
Application of derivativesA farmer decides to enclose a rectangular garden, using the side of a barn as one side of the rectangle. What is the maximum area that the farmer can enclose with
48 ft of fence? What should the dimensions of the garden be to give this area?
The maximum area that the farmer can enclose with 48 ft of fence is 288 sq ft.
The larger dimension of the garden to give this area is
*****
and the smaller dimension is
Math
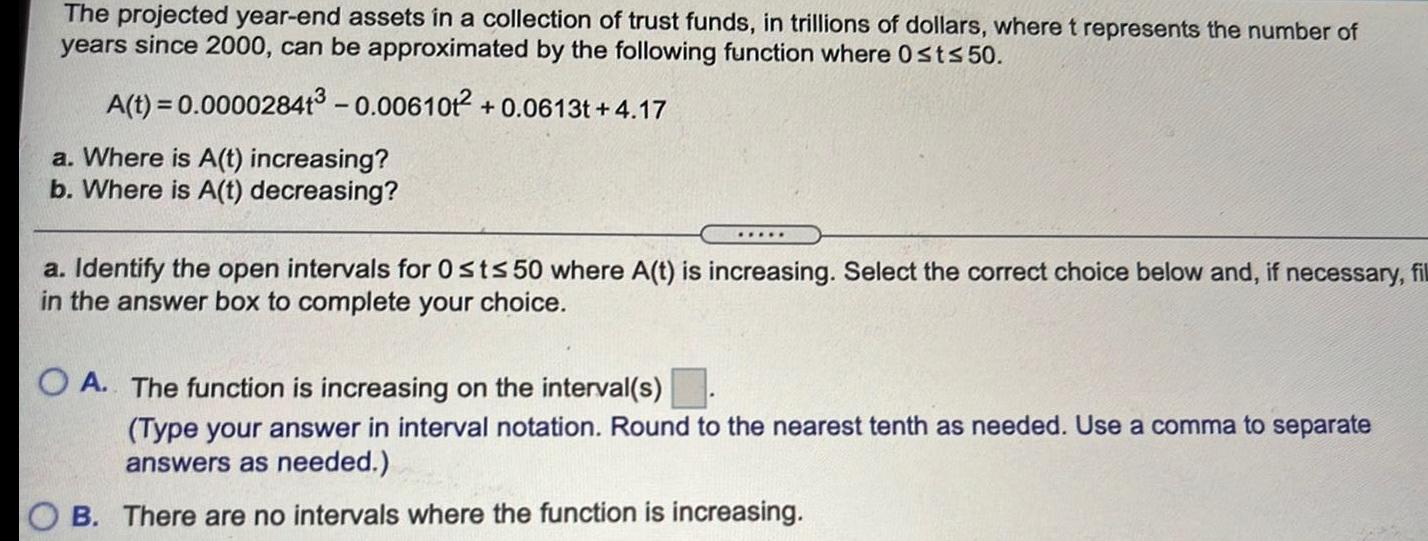
Application of derivativesThe projected year-end assets in a collection of trust funds, in trillions of dollars, where t represents the number of
years since 2000, can be approximated by the following function where Ost≤50.
A(t) = 0.000028413 -0.006101² +0.0613t+4.17
a. Where is A(t) increasing?
b. Where is A(t) decreasing?
a. Identify the open intervals for 0 st≤ 50 where A(t) is increasing. Select the correct choice below and, if necessary, fil
in the answer box to complete your choice.
A. The function is increasing on the interval(s).
(Type your answer in interval notation. Round to the nearest tenth as needed. Use a comma to separate
answers as needed.)
B. There are no intervals where the function is increasing.

Math
Application of derivativesThe radius r of a circle is increasing at a rate of 8 centimeters per minute. Find the rate of change of the area when
r = 30 centimeters.
cm²/min

Math
Application of derivativesA winch at the top of a 12-meter building pulls a pipe of the same length to a vertical position, as shown in the figure. The winch pulls in rope at a rate of -0.9 meter per second (ds/dt = -0.9 m/sec). Find the rate of vertical change and the rate of horizontal change at the end of the pipe when y = 3. (Round your answers to three decimal places.)

Math
Application of derivativesWhen a certain polyatomic gas undergoes adiabatic expansion, its pressure p and volume V satisfy the equation pv1.4 = k, where k is a constant. Find the relationship between the related rates dp/dt and dv/dt.
dV/dt=dp/dt
![Determine the location and value of the absolute extreme values of f on the given interval, if they exist.
f(x)=30x(1/2)-x on [0,900]
What is/are the absolute maximum/maxima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer
boxes to complete your choice.
A. The absolute maximum/maxima is/are at x =
(Use a comma to separate answers as needed.)
B. There is no absolute maximum of f on the given interval.](https://media.kunduz.com/media/sug-question/raw/60303582-1657215157.218361.jpeg?w=256)
Math
Application of derivativesDetermine the location and value of the absolute extreme values of f on the given interval, if they exist.
f(x)=30x(1/2)-x on [0,900]
What is/are the absolute maximum/maxima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer
boxes to complete your choice.
A. The absolute maximum/maxima is/are at x =
(Use a comma to separate answers as needed.)
B. There is no absolute maximum of f on the given interval.

Math
Application of derivativesConsider the following scenarios using two strings.
Part A: Is it possible to construct a square with the two strings? Explain your
answer.
Part B: Is it possible to construct a rectangle with the two strings? Explain
your answer.
Math
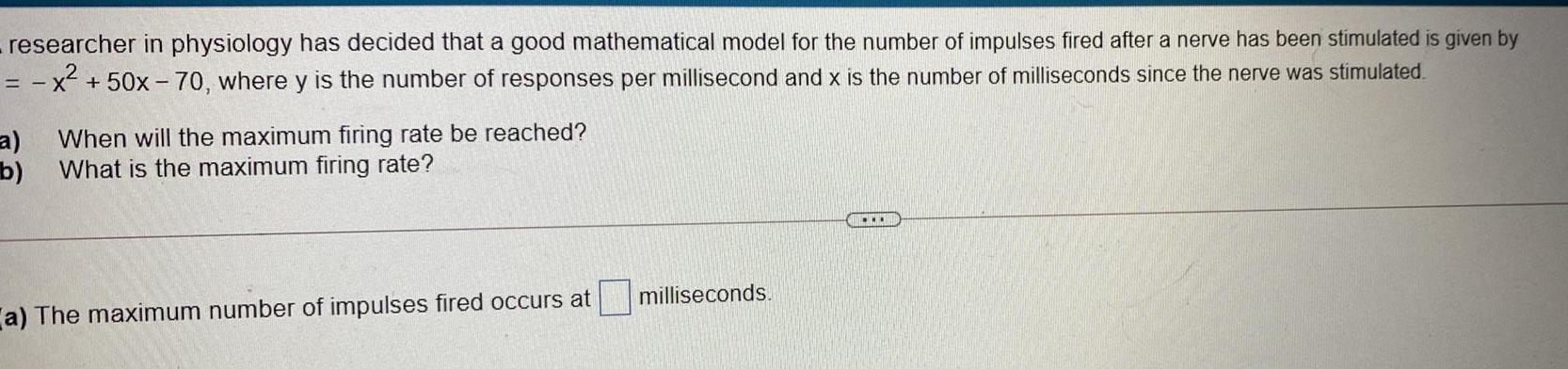
Application of derivativesA researcher in physiology has decided that a good mathematical model for the number of impulses fired after a nerve has been stimulated is given by y = -x² + 50x - 70, where y is the number of responses per millisecond and x is the number of milliseconds since the nerve was stimulated.
a) When will the maximum firing rate be reached?
b) What is the maximum firing rate?

Math
Application of derivativesIn t'years, the population of a certain city grows from 500,000 to a size P given by P(t) = 500,000 + 7000t².
a) Find the growth rate, dP/dt
b) Find the population after 20 yr.
c) Find the growth rate at t=20.
d) Explain the meaning of the answer to part (c).
a) dP/dt=
b) The population after 20 yr is.
(Simplify your answer.)
c) The growth rate at t = 20 is
(Simplify your answer.)
d) What is the meaning of the answer to part (c)?
A. The growth rate tells the difference between the rate of growth at the beginning of t=0 and t = 20.
B. The growth rate tells the average growth from time t = 0 and t = 20.
C. The growth rate tells the rate at which the population is growing at time t=20-1.
D. The growth rate tells the rate at which the population is growing at time t = 20.

Math
Application of derivativesAn accessories company finds that the cost, in dollars, of producing x belts is given by C(x) = 720+30x-0.064x². Find the rate at which average cost is changing when 172 belts have been produced.
First, find the rate at which the average cost is changing when x belts have been produced.
c=0
When 172 belts have been produced, the average cost is changing at for each additional belt.
(Round to four decimal places as needed)

Math
Application of derivativesThe profit, in thousands of dollars, from the sale of x thousand candles can be estimated by P(x) = 3x -0.7x In x. Complete parts (a) through (c).
a) Find the marginal profit, P'(x).
P'(x)=
b) Find P'(22), and explain what this number represents.
P'(22)=
(Type an integer or decimal rounded to the nearest thousandth as needed.)
What does P'(22) represent?
GICKEIR
OA. The additional profit, in thousands of dollars, when 22,000 candles are sold.
OB. The additional profit, in thousands of llars, for
OC. The additional cost, in thousands of dollars, to produce 22,000 candles.
OD. The additional cost, in thousands of dollars, to produce a thousand candles once 22,000 candles have already been sold.
c) How many thousands of candles should be sold to maximize profit?
(Type an integer or decimal rounded to the nearest thousandth as needed.)
thousand candles once 22,000 candles have already been sold.

Math
Application of derivativesFor f(x)=x², the instantaneous rate of change is known to be -4 at x = -2. Find the equation of the tangent line to the graph of y=f(x) at the point with x-coordinate - 2.
The equation of the tangent line to the graph at the point with x-coordinate - 2 is
(Type an equation. Use integers or fractions for any numbers in the equation.)

Math
Application of derivativesWhich of the following functions cannot use the Second Derivative Test to determine if x = 3 is the location of a relative minimum or relative maximum?

Math
Application of derivativesIf Bob is driving along a toll road and passes the first toll reader at 12:00 and is traveling 50 miles an hour, he then passes the secondreader 10 miles later at 12:10.
Using the Mean Value Theorem, can you find Bob's average speed? Can you prove that he must have been driving faster than 55 miles per hour at some point?
Bob's average speed was 60 miles/hr and the Mean Value Theorem cannot be used to prove that he was traveling faster than 55 miles per hour at some point between the two toll readers.
Bob's average speed was 50 miles/hr and the Mean Value Theorem cannot be used to prove that he was traveling faster than 55 miles per hour at some point between the two toll readers.
Bob's average speed was 50 miles/hr and the Mean Value Theorem can be used to prove that he was traveling faster than 55 miles per hour at some point between the two toll readers.
Bob's average speed was 60 miles/hr and the Mean Value Theorem can be used to prove that he was traveling faster than 55 miles per hour at some point between the two toll readers.

Math
Application of derivativesSue opens a bank account with $1 and an interest rate of 3% per year, compounded continuously. The amount of money in the account can be described by A = le^=(1.03)
Assuming interest is being paid continuously, what is the instantaneous rate of change of the account at t = 10 years?
The instantaneous rate of change of the account at t = 10 years is $3 per year.
The instantaneous rate of change of the account at t= 10 years is $30,624 per year.
The instantaneous rate of change of the account at t= 10 years is $20 per year.
The instantaneous rate of change of the account at t = 10 years is $306 per year.

Math
Application of derivativesA camera is tracking the flight of a rocket as it launches from the platform. At this moment, the rocket
is 7.16 miles up and is rising with a velocity of 1,200 mph. If the camera is 2 miles away from the
launch platform, how quickly is the camera angle increasing at this time?