Application of derivatives Questions and Answers
![Find the equation of the tangents to the curve y = sin x at x = - π/2, π and 2π. Graph the curve over the interval [-3π/2,3π] together with their tangents. Label each curve and tangent.](https://media.kunduz.com/media/sug-question/raw/58481110-1657731625.149962.jpeg?w=256)
Math
Application of derivativesFind the equation of the tangents to the curve y = sin x at x = - π/2, π and 2π. Graph the curve over the interval [-3π/2,3π] together with their tangents. Label each curve and tangent.

Math
Application of derivativesIf an arrow is shot upward on the moon with a velocity of 58 m/sec, if height (m) after t seconds is given by: h(t)= 58 t - 0.83 t². The instantaneous velocity of the arrow after 1.3 seconds is approximately:
a. 74 m/sec
O b. 56 m/sec
O c. 60 m/sec
Od-56 m/sec
![Exercise 5. [10 pts] According to a simplified economic model, the purchasing power of 1 dollar
in the year 2000+ t is equal to
P(t) 0.68(1.040)-²
dollars. Calculate (you will need a calculator) the rate of change of the purchasing power in the
year 2025 as predicted by this model.](https://media.kunduz.com/media/sug-question/raw/58241050-1657718864.5017772.jpeg?w=256)
Math
Application of derivativesExercise 5. [10 pts] According to a simplified economic model, the purchasing power of 1 dollar
in the year 2000+ t is equal to
P(t) 0.68(1.040)-²
dollars. Calculate (you will need a calculator) the rate of change of the purchasing power in the
year 2025 as predicted by this model.
![Request Extension
-15 -15
-15
y' =
-15
Find the derivative of the function.
y = In(xvx²-5)
17
4
-15
18
-15
17. [-/5 Points] DETAILS LARCALC11 5.1.051.
19 20
-15 -15
Assignment Submission & Scoring
Assignment Submission
For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only
changes if you submit or change the answer.
Assignment Scoring
Your last submission is used for your score.
TOTAL SCORE
-/100 0.0%](https://media.kunduz.com/media/sug-question/raw/58271258-1657718565.7554958.jpeg?w=256)
Math
Application of derivativesRequest Extension
-15 -15
-15
y' =
-15
Find the derivative of the function.
y = In(xvx²-5)
17
4
-15
18
-15
17. [-/5 Points] DETAILS LARCALC11 5.1.051.
19 20
-15 -15
Assignment Submission & Scoring
Assignment Submission
For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only
changes if you submit or change the answer.
Assignment Scoring
Your last submission is used for your score.
TOTAL SCORE
-/100 0.0%

Math
Application of derivativesThe revenue equation (in hundreds of millions of dollars) for barley production in a certain country is approximated by R(x)=0.0673x² +1.2883x+2.2308 where x is in hundreds of millions of bushels. Find the marginal-revenue equation and use it to find the marginal revenue for the production of the given number of bushels.
(a) The marginal-revenue equation is R'(x) =
(Round to four decimal places as needed.)
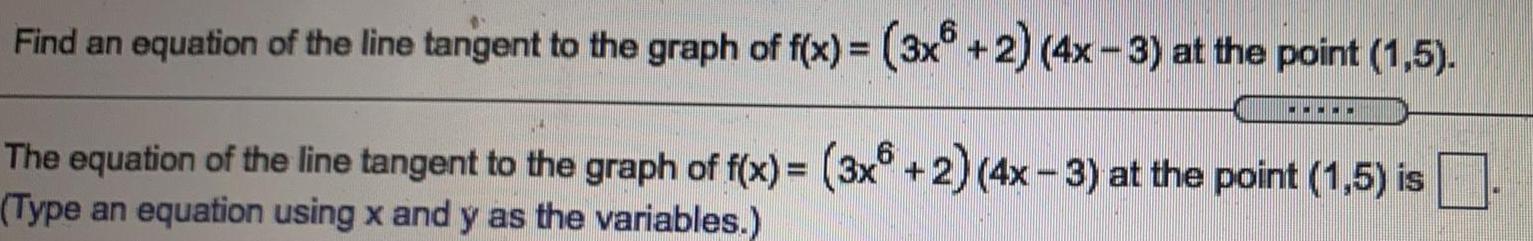
Math
Application of derivativesFind an equation of the line tangent to the graph of f(x) = (3x + 2) (4x-3) at the point (1,5).
The equation of the line tangent to the graph of f(x) = (3x + 2) (4x - 3) at the point (1,5) is
(Type an equation using x and y as the variables.)
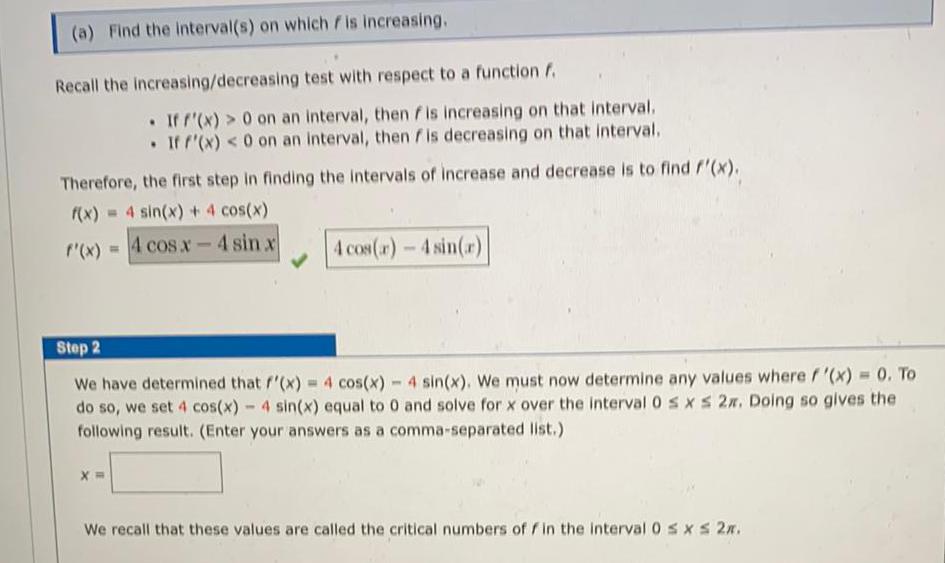
Math
Application of derivatives(a) Find the interval(s) on which is increasing.
Recall the increasing/decreasing test with respect to a function f.
• If f'(x) > 0 on an interval, then fis increasing on that interval.
• If f'(x) < 0 on an interval, then fis decreasing on that interval.
Therefore, the first step in finding the intervals of increase and decrease is to find f'(x).
f(x) = 4 sin(x) + 4 cos(x)
f'(x) = 4 cos.x - 4 sin x
Step 2
We have determined that f'(x) = 4 cos(x) - 4 sin(x). We must now determine any values where f'(x) = To do so, we set 4 cos(x) - 4 sin(x) equal to 0 and solve for x over the interval 0 ≤ x ≤ 2x. Doing so gives the following result. (Enter your answers as a comma-separated list.)
x=
We recall that these values are called the critical numbers of f in the interval 0 ≤ x ≤ 2x.

Math
Application of derivativesA short length of blood vessel has a cylindrical shape. The volume of a cylinder is given by V=πr²h. Suppose an experimental device is set up to measure the volume of blood in a blood vessel of fixed length 80 mm as the radius changes. Complete parts (a) through
(d) below.
(a) Find dV/dr
dV/dr=

Math
Application of derivativesIf an object is projected upward from ground level with an initial velocity of 32 ft per sec, then its height in feet after t seconds is given by s(t)= - 16t2 +32t. Find the number of seconds it will take to reach its maximum height. What is this maximum height?

Math
Application of derivativesSand falls from a conveyor belt at a rate of 14 m/min onto the top of a conical pile. The height of the pile is always three-eighths of the base diameter. How fast are the height and the radius changing when the pile is 8 m high?
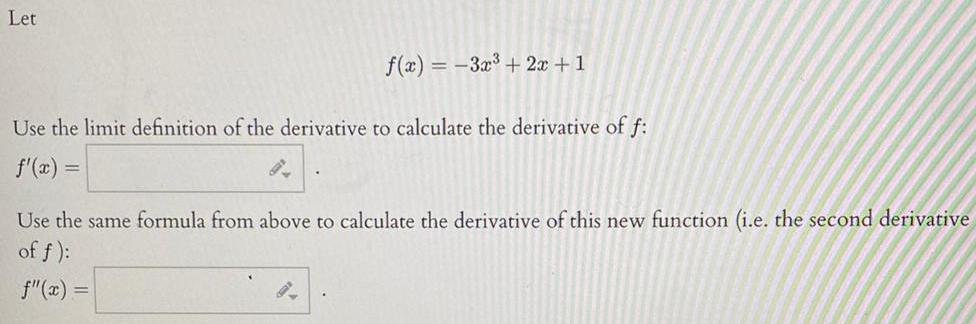
Math
Application of derivativesLet
f(x) = -3x³ + 2x + 1
Use the limit definition of the derivative to calculate the derivative of f:
f'(x) =
Use the same formula from above to calculate the derivative of this new function (i.e. the second derivative
of f):
f"(x) =

Math
Application of derivativesSand falls from a conveyor belt at a rate of 9 m³/min onto the top of a conical pile. The height of the pile is always three-eighths of the base diameter. How fast are the height and the radius changing when the pile is 5 m high?
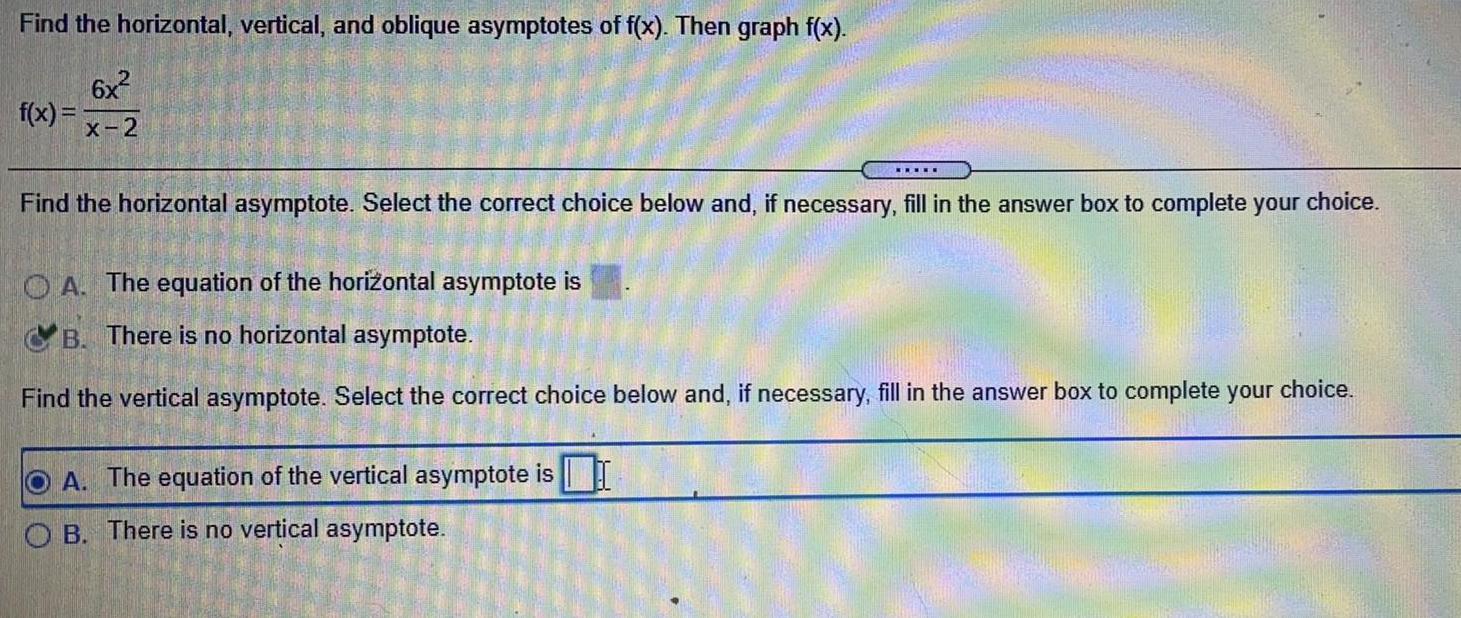
Math
Application of derivativesFind the horizontal, vertical, and oblique asymptotes of f(x). Then graph f(x).
f(x)=6x²/x-2
Find the horizontal asymptote. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The equation of the horizontal asymptote is
B. There is no horizontal asymptote.
Find the vertical asymptote. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The equation of the vertical asymptote is
B. There is no vertical asymptote.

Math
Application of derivativesA toy rocket is shot vertically into the air from a launching pad 4 feet above the ground with an initial velocity of 152 feet per second. The height h, in feet, of the rocket above the ground at t seconds after launch is given by the function h(t)= - 16t² + 152t + 4. How long will it take the rocket to reach its maximum height? What is the maximum height?
Math
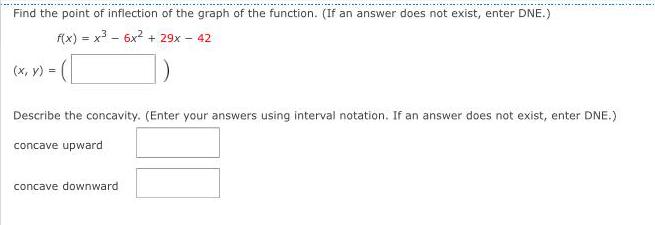
Application of derivativesFind the point of inflection of the graph of the function. (If an answer does not exist, enter DNE.)
f(x) = x³ - 6x² + 29x - 42
(x, y) =
Describe the concavity. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)
concave upward
concave downward
![Please show all your work in order to get full credit.
1.) Let
f(x,y) = x/y
Find the derivative (for)'(t) in two ways:
F(t) = (e², e³¹).
(i) (1 pt) First compute the composition (for) (t), get a calc 1 function,
take the derivative.
(ii) (2 pts) Using the chain rule (for)'(t) = [Vf(r(t))][].](https://media.kunduz.com/media/sug-question/raw/57615491-1657653990.962956.jpeg?w=256)
Math
Application of derivativesPlease show all your work in order to get full credit.
1.) Let
f(x,y) = x/y
Find the derivative (for)'(t) in two ways:
F(t) = (e², e³¹).
(i) (1 pt) First compute the composition (for) (t), get a calc 1 function,
take the derivative.
(ii) (2 pts) Using the chain rule (for)'(t) = [Vf(r(t))][].
Math
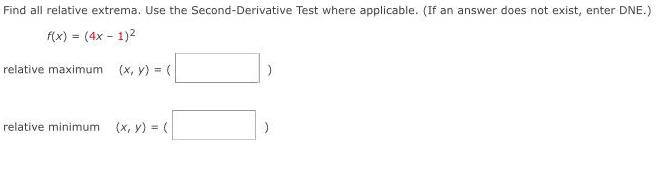
Application of derivativesFind all relative extrema. Use the Second-Derivative Test where applicable. (If an answer does not exist, enter DNE.)
f(x) = (4x - 1)²

Math
Application of derivativesA baseball diamond is a square with side 90 feet. A batter hits the ball and runs toward first base with a speed of 31 ft/s.
(a) At what rate (in ft/s) is his distance from second base decreasing when he is halfway to first base?
(b) At what rate (in ft/s) is his distance from third base increasing at the same moment?
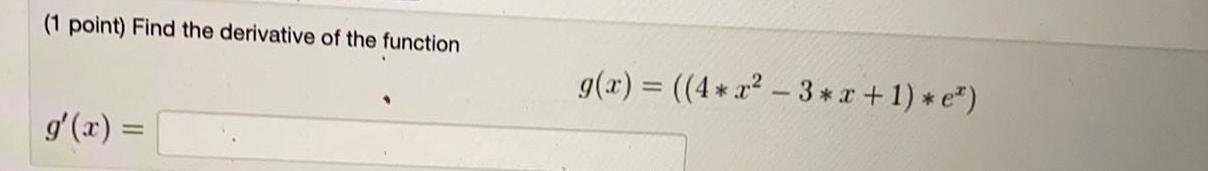
Math
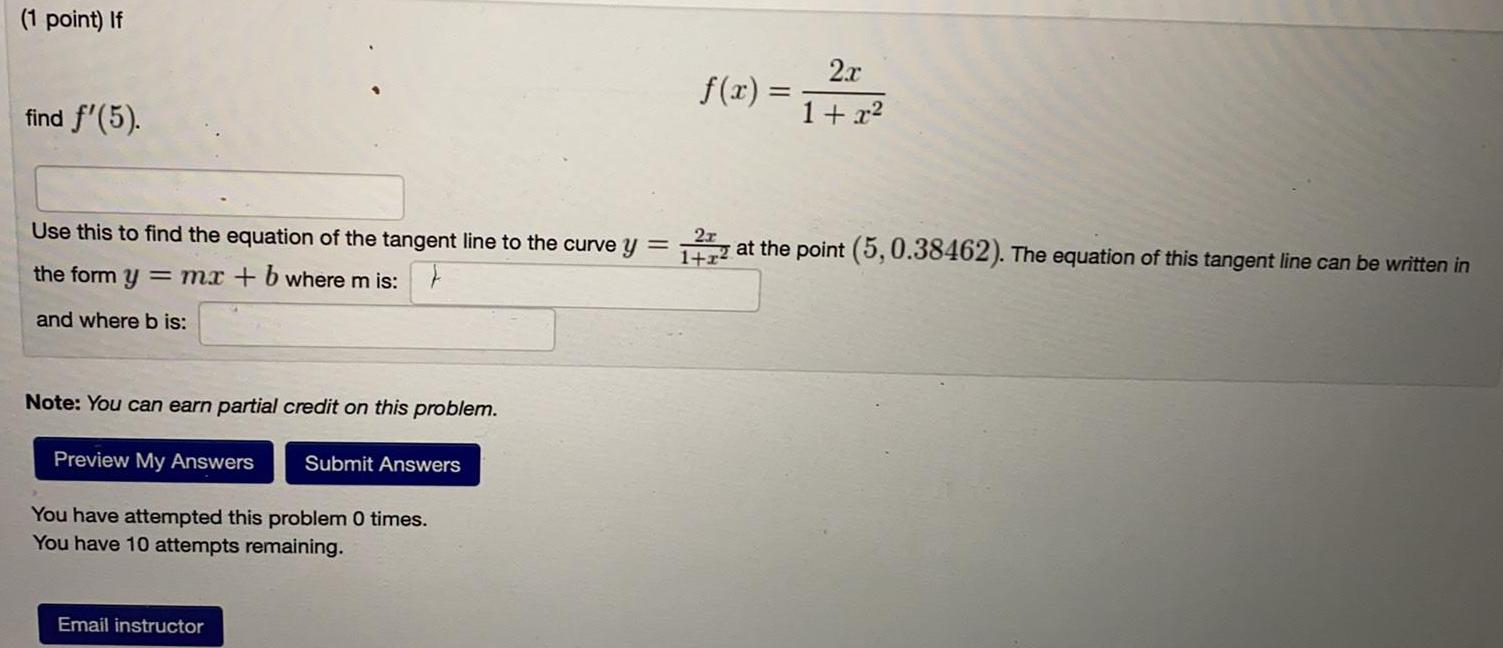
Application of derivatives(1 point) If
find f'(5).
Use this to find the equation of the tangent line to the curve y
=
the form y = mx + b where m is:
and where b is:
Note: You can earn partial credit on this problem.
Preview My Answers Submit Answers
You have attempted this problem 0 times.
You have 10 attempts remaining.
Email instructor
f(x) =
2x
1+x²
2r
12 at the point (5, 0.38462). The equation of this tangent line can be written in

Math
Application of derivativesThe path of a toy rocket is defined by the
relation y = -3x² + 11x + 4, where x is
the horizontal distance, in metres,
travelled and y is the height, in metres,
above the ground.
a) Determine the zeros of the relation.
b) For what values of x is the relation
valid?
c) How far has the rocket travelled
horizontally when it lands on the
ground?
d) What is the maximum height of the
rocket above the ground, to the nearest
hundredth of a metre?

Math
Application of derivativesA street light is mounted at the top of a 15-ft-tall pole. A man 6 feet tall walks away from the pole with a speed of 7 ft/s along a straight path. How fast (in ft/s) is the tip of his shadow moving when he is 35 feet from the pole?

Math
Application of derivativesThe path of a toy rocket is given by P (t) = -(t-3)² + 21, where t is in seconds, and P is in meters. When is the maximum height reached by the rocket?
(A) -3 seconds
B) 2 seconds
c) 0 seconds
D) 3 seconds

Math
Application of derivativesA point moves along the curve y = x² + 1 such that its x-coordinate is increasing at the rate of per second. At what rate is the point's distance from the origin changing when the point is at (1, 2)?

Math
Application of derivativesA thin sheet of ice on the university sidewalk is in the form of a circle. With the sun out and the wind blowing, the area of the ice is melting at a rate of 0.5 m²/sec. How fast is the radius changing when the area of the ice is 12 m²?

Math
Application of derivativesThe tangent line to the graph of y = f(x) at the point (1,8) has the equation y = 7x + 1.
(a) Find f'(1).
ƒ'(1) =
(b) Find the instantaneous rate of change of y with respect to x at x = = 1.
Instantaneous Rate of Change =
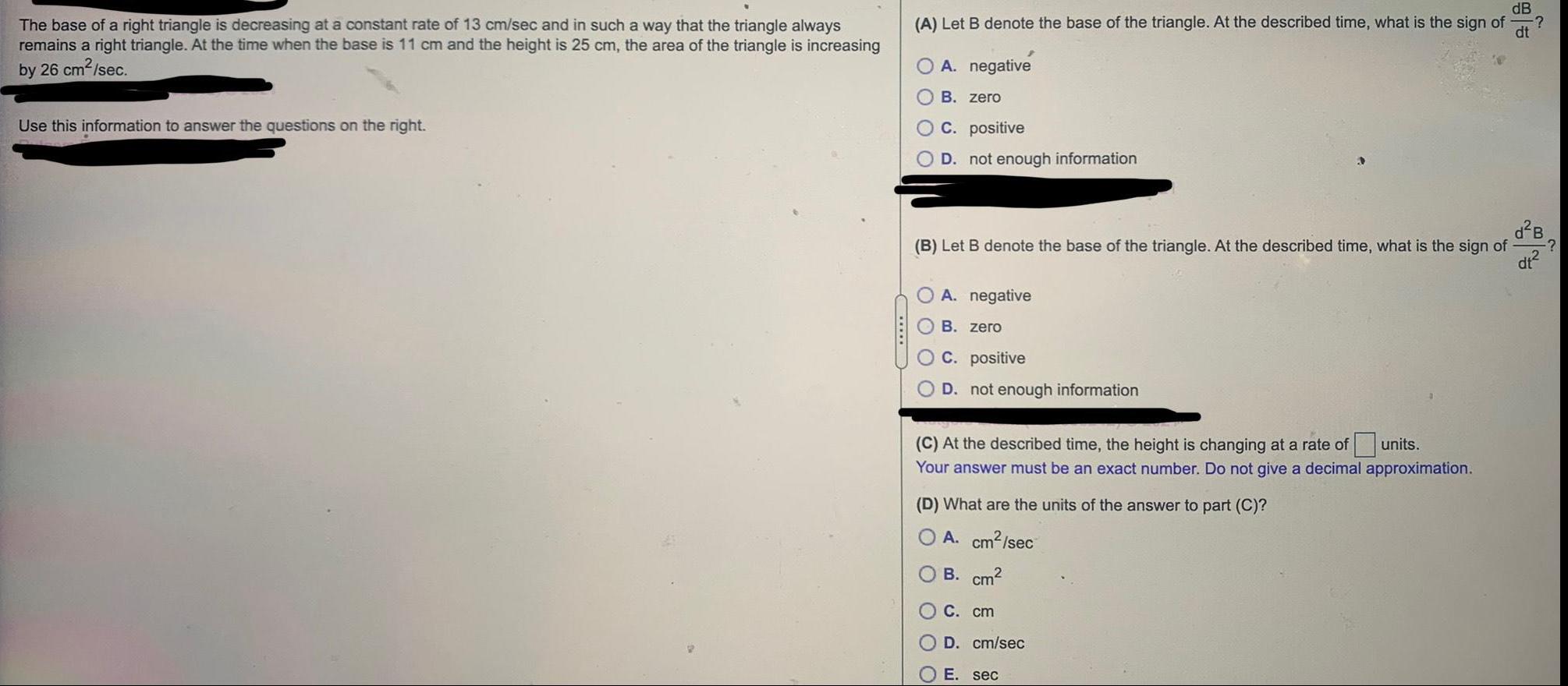
Math
Application of derivativesThe base of a right triangle is decreasing at a constant rate of 13 cm/sec and in such a way that the triangle always
remains a right triangle. At the time when the base is 11 cm and the height is 25 cm, the area of the triangle is increasing
by 26 cm²/sec.
Use this information to answer the questions on the right.
dB
(A) Let B denote the base of the triangle. At the described time, what is the sign of dt
?
2
A. negative
B. zero
C. positive
D. not enough information
(B) Let B denote the base of the triangle. At the described time, what is the sign of
d²B
dt²
OA. negative
OB. zero
OC. positive
D. not enough information
(C) At the described time, the height is changing at a rate of units.
Your answer must be an exact number. Do not give a decimal approximation.
(D) What are the units of the answer to part (C)?
O A. cm²/sec
B. cm²
C. cm
D. cm/sec
E. sec
-?

Math
Application of derivativesAmong all rectangles that have a perimeter of 188, find the dimensions of the one whose area is largest. Write your answers as fractions reduced to lowest terms.

Math
Application of derivativesThe total revenue for Fred's Estates LLC is given as the function R(x) = 100x - 0.4x², , where x is the number of rooms rented. What number of rooms rented produces the maximum revenue?

Math
Application of derivativesA new movie theater holds 300 people. They found that when the price was $8 per ticket, the
average sales would be 250 people per show. Each time they increase the price by $1, the average
attendance drops by 15 people. What price should they charge in order to maximize revenue?
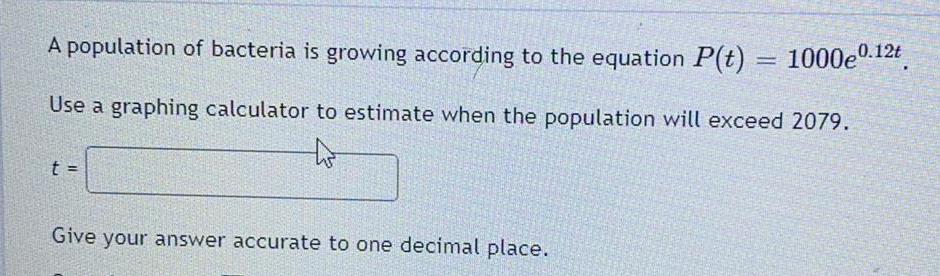
Math
Application of derivativesA population of bacteria is growing according to the equation P(t) = 1000e^0.12t
Give your answer accurate to one decimal place.
Use a graphing calculator to estimate when the population will exceed 2079.

Math
Application of derivativesA heap of rubbish in the shape of a cube is being compacted into a smaller cube. Given that the volume decreases at a rate of 4 cubic meters per minute, find the rate of change of an edge, in meters per minute, of the cube when the volume is exactly 125 cubic meters.

Math
Application of derivativesA sales representative for a company that produces toasters can sell x units of their deluxe model if the price is p = D(x) = 71.7 -0.04x dollars. The total cost for these toasters is given by C(x) = 0.05x² + 5.3x + 6600 dollars. Determine the marginal profit for 95 toasters.
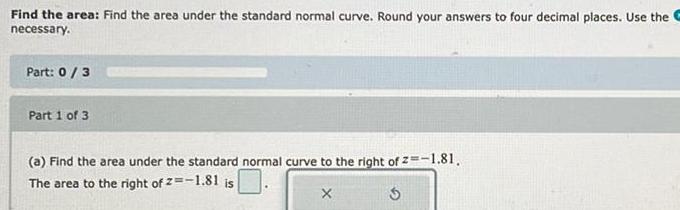
Math
Application of derivativesFind the area under the standard normal curve. Round your answers to four decimal places. Use the necessary.
(a) Find the area under the standard normal curve to the right of z=-1.81.
The area to the right of z=-1.81 is

Math
Application of derivativesA rancher has 800 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to
one of the field's shorter sides. Find the dimensions that maximize the enclosed area. Write your answers as fractions reduced to lowest terms.

Math
Application of derivativesThe population P of a small town, measured in hundreds, is modeled by the inverse of the function P-1(t) = 10ln(50t - 1000), where t is measured in years. Find the equation to
model the population and determine its initial value.
P = 5t + 100 where P(0) = 100
P=
P=
P=
50
In(0.1t) + 20
1
500
50
-e' +20
0.11
+20
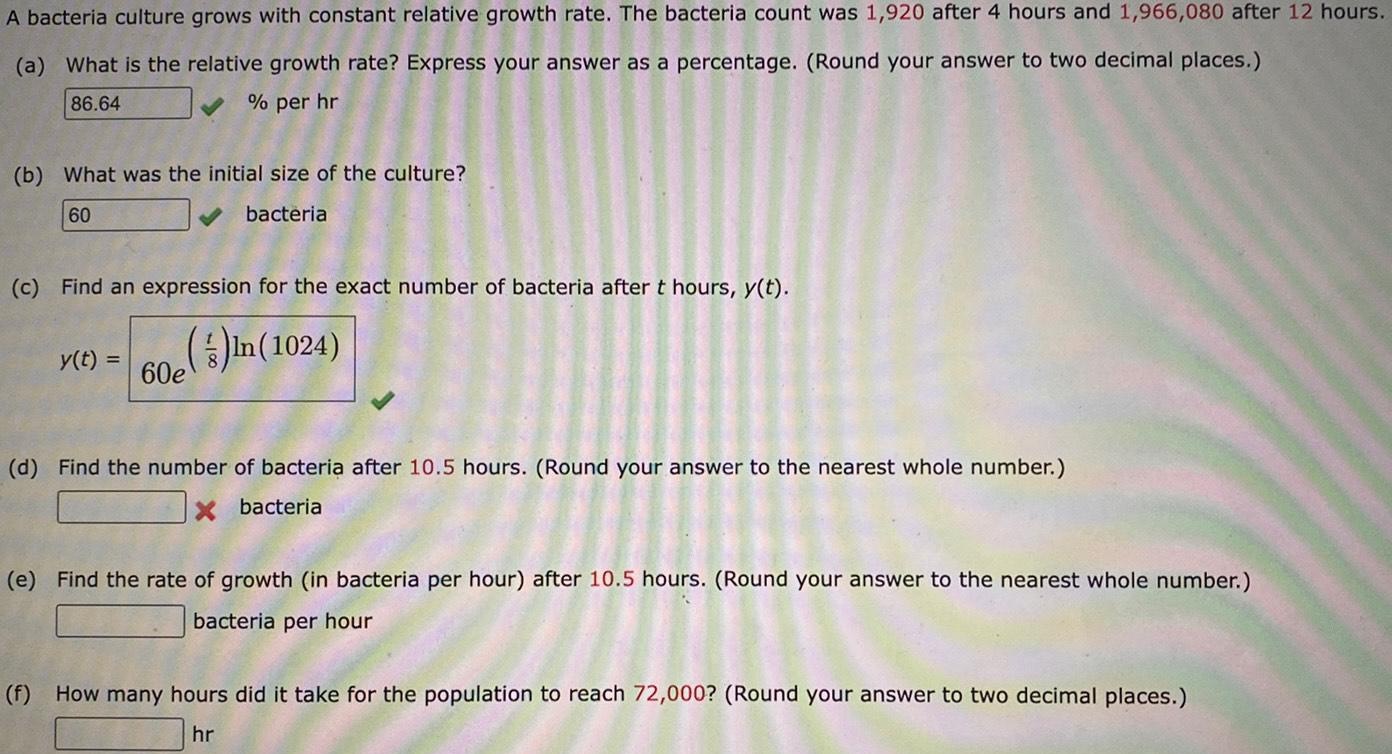
Math
Application of derivativesA bacteria culture grows with constant relative growth rate. The bacteria count was 1,920 after 4 hours and 1,966,080 after 12 hours.
(a) What is the relative growth rate? Express your answer as a percentage. (Round your answer to two decimal places.)
86.64
% per hr
(b) What was the initial size of the culture?
60
bacteria
(c) Find an expression for the exact number of bacteria after t hours, y(t).
()in (1024)
y(t) =
60e
(d) Find the number of bacteria after 10.5 hours. (Round your answer to the nearest whole number.)
X bacteria
(e) Find the rate of growth (in bacteria per hour) after 10.5 hours. (Round your answer to the nearest whole number.)
bacteria per hour
(f) How many hours did it take for the population to reach 72,000? (Round your answer to two decimal places.)
hr

Math
Application of derivativesSuppose that the dollar cost of producing x appliances is c(x) = 1400 + 90x-0.1x².
a. Find the average cost per appliance of producing the first 110 appliances.
b. Find the marginal cost when 110 appliances are produced.
c. Show that the marginal cost when 110 appliances are produced is approximately the cost of producing one more appliance after the first 110 have been made, by calculating the latter cost directly

Math
Application of derivativesA rectangular solid with a square base has a volume of 1,728 cubic inches. (Let w represent the length of the sides of the square base and let h represent the height of the solid.)
(a) Determine the dimensions (in inches) that yield the minimum surface area.
W =
h =
in
in ²
in
(b) Find the minimum surface area (in in.2).
Math
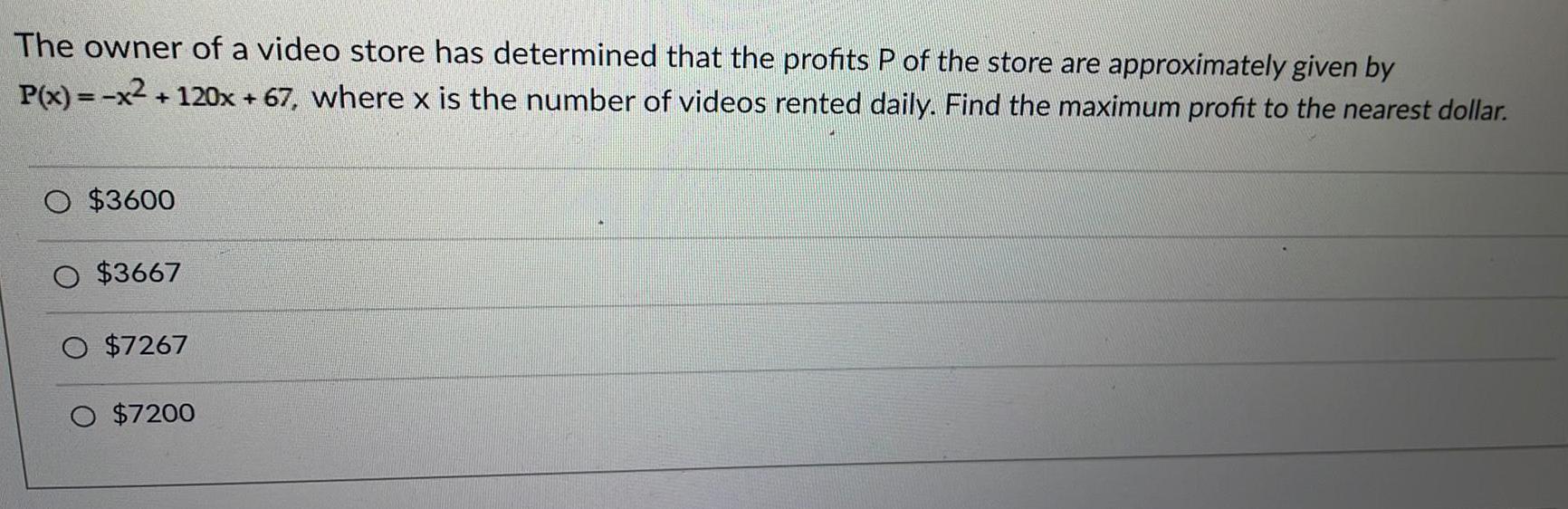
Application of derivativesThe owner of a video store has determined that the profits P of the store are approximately given by P(x) = -x². +120x+67, where x is the number of videos rented daily. Find the maximum profit to the nearest dollar.
$3600
$3667
$7267
$7200
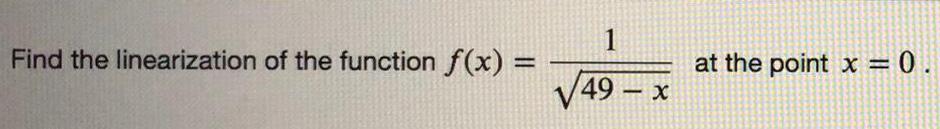
Math
Application of derivativesFind the linearization of the function f(x) =
1
√49 - x
at the point x = 0.
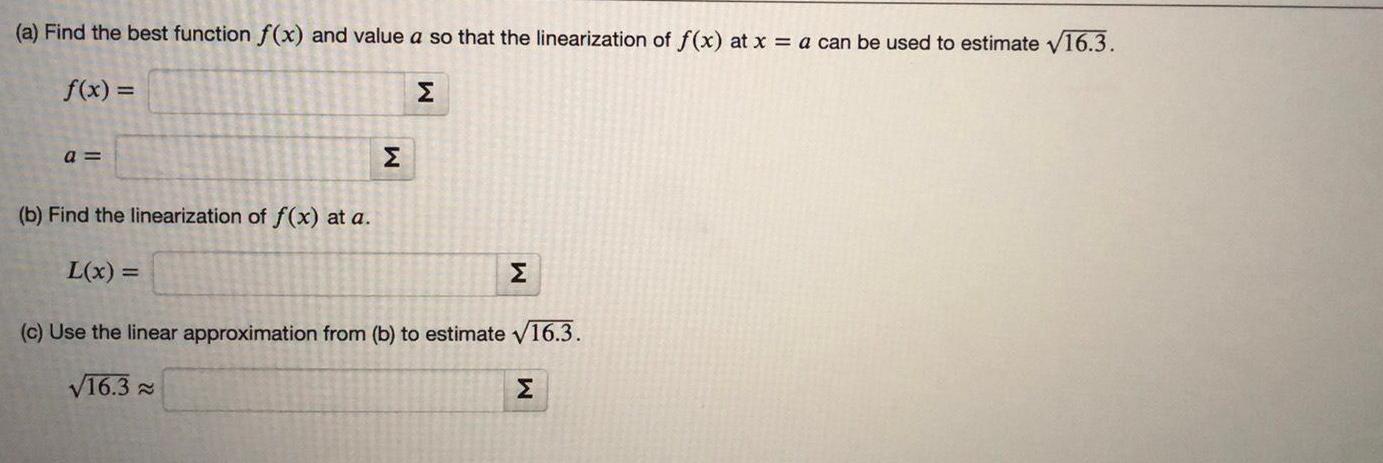
Math
Application of derivatives(a) Find the best function f(x) and value a so that the linearization of f(x) at x = a can be used to estimate √16.3.
f(x) =
a =
(b) Find the linearization of f(x) at a.
L(x) =
M
M
(c) Use the linear approximation from (b) to estimate √16.3.
√16.3
M

Math
Application of derivatives54
Which of the following is true about the graph of f(x) = 64x² + X
a) O f(x) is concave down on the interval (0, ∞).
b) O f(x) has a vertical asymptote at æ = 54.
c) O f(x) has a point of inflection at the point (0, -2).
(3,106)
d) O f(x) has a local minimum at the point
e) Of(x) is increasing on the interval (-∞, 0).
-
2?

Math
Application of derivativesFind the critical numbers of the function. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
f(x) = 2x³ + x² + 4x
X =
6x² + 2x + 4
X

Math
Application of derivativesLet V represent the volume of a sphere with radius r mm. Write an equation for V (in mm³) in terms of r.
mm 3
V(r) =
Find the radius of a sphere (in mm) when its diameter is 60 mm.
r =
mm
The radius of a sphere is increasing at a rate of 2 mm/s. How fast is the volume increasing (in mm³/s) when the diameter is
60 mm? (Round your answer to two decimal places.)
mm³/s
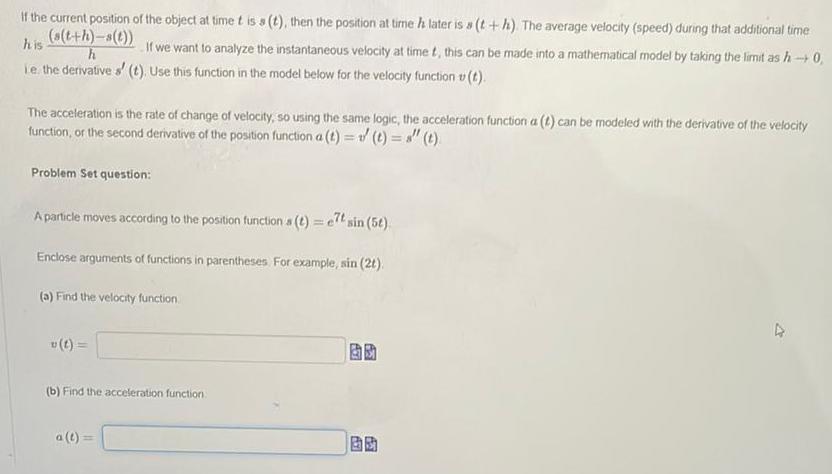
Math
Application of derivativesIf the current position of the object at time t is s (t), then the position at time h later is s (t+h). The average velocity (speed) during that additional time h is (s(t+h)-s(t)) / h
If we want to analyze the instantaneous velocity at time t, this can be made into a mathematical model by taking the limit as h→0, i.e. the derivative s' (t). Use this function in the model below for the velocity function v (t).
The acceleration is the rate of change of velocity, so using the same logic, the acceleration function a (t) can be modeled with the derivative of the velocity function, or the second derivative of the position function a(t) = v' (t)= s" (t)
Problem Set question:
A particle moves according to the position functions (t) = e7t sin (5t)
Enclose arguments of functions in parentheses. For example, sin (2t).
(a) Find the velocity function.
(b) Find the acceleration function

Math
Application of derivativesChase has 60 feet of Halloween lights he wants to string around the perimeter of an enclosure that he will build. It is to be rectangular with a semi-circle on one edge, as shown in the drawing below. What is the maximum size of the area of the enclosure that he can build with his limited light string?
a) Write an equation for the area with respect to the radius of the semi-circle.
b) What radius and length and width of rectangle will maximize the area?
c) What will that maximum area be?

Math
Application of derivativesThe total amount spent by some number of people on clothing and footwear in the years 2000-2009 can be modeled by the quadratic function f(x) = -4.867x² + 72.73x +97.86, where x = 0 represents January
2000, x= 1 represents January 1, 2001, and so on, and f(x) is in billions of dollars. According to the model, in what year during this period was the amount spent on clothing and footwear a maximum?

Math
Application of derivativesA filter filled with liquid is in the shape of a vertex-down cone with a height of 9 inches and a diameter of 6 inches at its open (upper) end. If the liquid drips out the bottom of the filter at the constant rate of 4 cubic inches per second, how fast is the level of the liquid dropping when the liquid is 3 inches deep?
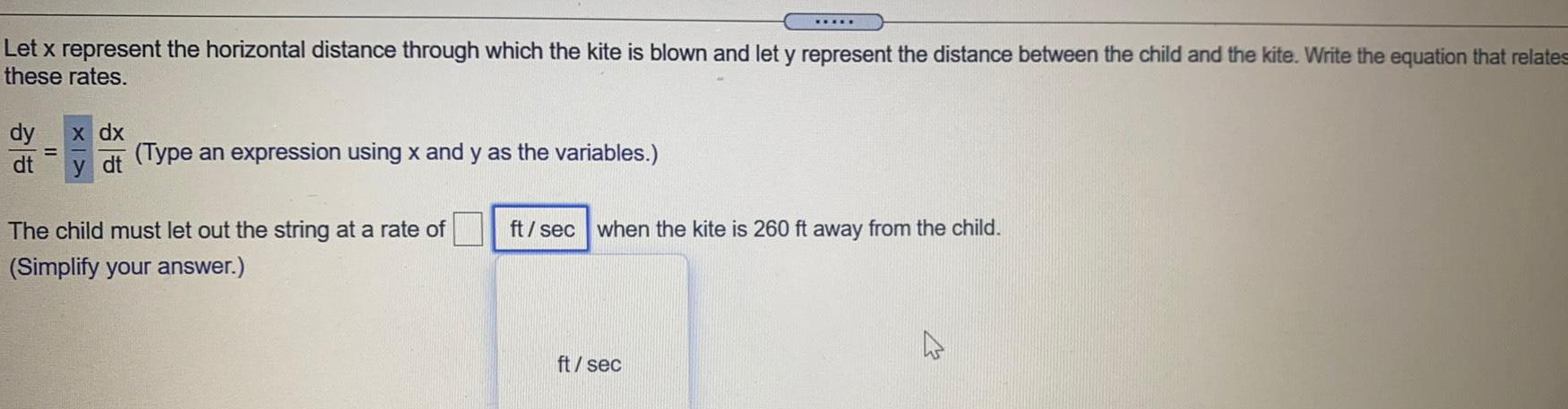
Math
Application of derivativesLet x represent the horizontal distance through which the kite is blown and let y represent the distance between the child and the kite. Write the equation that relates
these rates.
dy
dt