Basic Math Questions and Answers

Math
Basic MathNeglecting air resistance, the distance s(t) in feet traveled by a freely falling object is given by the function s(t)=16t2, where t is time in seconds. The height of a certain tower is 1005 feet. How long would it take an object to fall to the ground from the top of the building?
seconds

Math
Basic MathOfficer James has noticed a strong positive correlation between the speed of the vehicles on Main Street and the number of accidents. In order to determine if the speed is causing the accidents, which experiment would be best?
Officer James could make cars go fast and see if they crash.
Officer James could view traffic cameras to determine the speed of some cars and compare the speed of the cars that wrecked to the speed of those that did not.
Officer James could survey everyone who is in an accident and ask how fast they were going.
Officer James could try to find someone who got in an accident while driving slowly.

Math
Basic MathIt takes Doug 7 minutes to fill a bucket of blueberries and Nathan 10 minutes to fill the same size bucket. How long will it take them to fill 8 buckets of blueberries if they are working together?
Approximately 28 minutes.
Approximately 40 minutes.
Approximately 33 minutes.
Approximately 36 minutes.

Math
Basic MathSuppose that $2900 is borrowed for four years at an interest rate of 9% per year, compounded continuously. Find the amount owed, assuming no payments are made until the end.
Do not round any intermediate computations, and round your answer to the nearest cent.

Math
Basic MathAt a particular restaurant, each onion ring has 40 calories and each mini hotdog has 80 calories. A combination meal with onion rings and mini hotdogs has a total of 19 onion rings and mini hotdogs altogether and contains 1080 calories. Write a system of equations that could be used to determine the number of onion rings in the combination meal and the number of mini hotdogs in the combination meal. Define the variables that you use to write the system.

Math
Basic Math9. The time required to deliver and install a computer at a customer's location is t = 4+, where t is time in hours, d is the distance, in miles, from the warehouse to the customer's location, and r is the average speed of the delivery truck. If it takes 6.2 hours for the employee to deliver and install a computer for a customer located 100 miles from the warehouse, what is the average speed of the delivery truck?

Math
Basic MathThe exponential model A=363.1 e 0.027t describes the population, A, of a country in millions, t years after 2003. Use the model to determine when the population of the country will be 676 million.
The population of the country will be 676 million in
(Round to the nearest year as needed.)

Math
Basic MathA high times interest earned ratio indicates
a. no protection in the event of an earnings decline.
b. mediocre protection in the event of an earnings decline.
c. extremely good protection in the event of an earnings decline.
d. nothing about protection in the event of an earnings decline.

Math
Basic Math(a) Estimate the area under the graph of f(x) = 1 + x² from x= -1 to x 2 using three rectangles and right endpoints. Then improve your estimate by using six rectangles. Sketch the curve and the approximating rectangles.
(b) Repeat part (a) using left endpoints.
(c) Repeat part (a) using midpoints.
(d) From your sketches in parts (a)-(c), which appears to be the best estimate?

Math
Basic Math8. There are 9 red, 6 blue, and 5 green marbles in a bag.
a. How many marbles are in the bag?
b. What is the probability a marble chosen at random will be blue?

Math
Basic MathWhich of the following represents the explicit formula for the Arithmetic Sequence?
-33, -29, -25, -21, ....
Hint: a₁ = -33, so when n = 1, a₁ = -33.... Find the formula for an.
an-37 + 4n
an-33 + 2n
an-31 + 2n
an-33 + 4n

Math
Basic MathA certain loan program offers an interest rate of 2.5%, compounded continuously. Assuming no payments are made, how much would be owed after six years on a loan of $1300?
Do not round any intermediate computations, and round your answer to the nearest cent.

Math
Basic MathIf $2000 is invested at 6% compounded continuously, what is the amount after 8 years?
The amount after 8 years will be $

Math
Basic MathThe average yearly salary of a lawyer is $33 thousand less than twice that of an architect. Combined, an architect and a lawyer earn $210 thousand. Find the average yearly salary of an architect and a lawyer.

Math
Basic MathFind all complex zeros of the polynomial function. Give exact values. List multiple zeros as necessary
f(x)=x4-9x³-15x² +325x-750

Math
Basic MathThere are 3 balls in a hat; one with the number 2 on it, one with the number 6 on it, and one with the number 8 on it. You pick a ball from the hat at random and then you flip a coin. Using a tree diagram, obtain the sample space for the experiment. List the elements that make up the sample space.
A. 2 H, 6 H, 8H
B. 268 H, 268 T
C. 2HT, 6 HT, 8HT
D. 2 H, 2 T, 6 H, 6T, 8H, ST

Math
Basic MathA company's lawn seed mixtures contain three types of seeds: bluegrass, rye, and Bermuda. The costs per pound of the three types are 13 cents, 18 cents, and 7 cents, respectively. In each batch there must be at least 20% bluegrass seed and the amount of rye must be at least two-thirds the amount of Bermuda. To fill current
orders the company must make at least 9000 pounds of the mixture. How much of each kind of seed should be used to minimize cost?
The minimum cost of $ occurs with a mixture of pounds of bluegrass seed, pounds of rye seed, and pounds of Bermuda seed.
(Simplify your answers. Do not include the $ symbol in your answers.)
Math
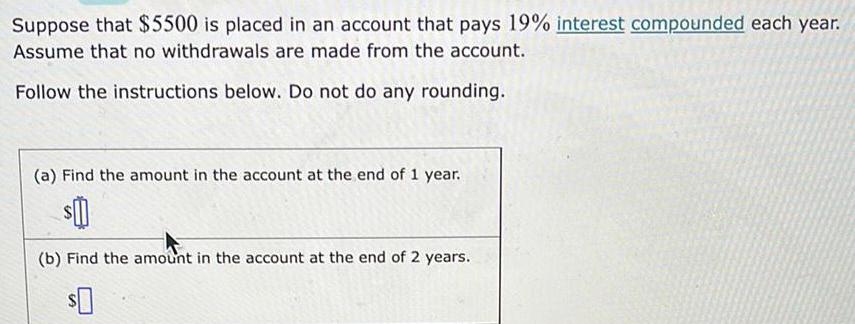
Basic MathSuppose that $5500 is placed in an account that pays 19% interest compounded each year.
Assume that no withdrawals are made from the account.
Follow the instructions below. Do not do any rounding.
(a) Find the amount in the account at the end of 1 year.
(b) Find the amount in the account at the end of 2 years.
$

Math
Basic MathA restaurant has an annual demand for 909 bottles of California wine. It costs $3 to store 1 bottle for 1 year, and it costs $10 to place a reorder. Find the optimum number of bottles per order.
The optimum number of bottles per order is. (Type a whole number.)
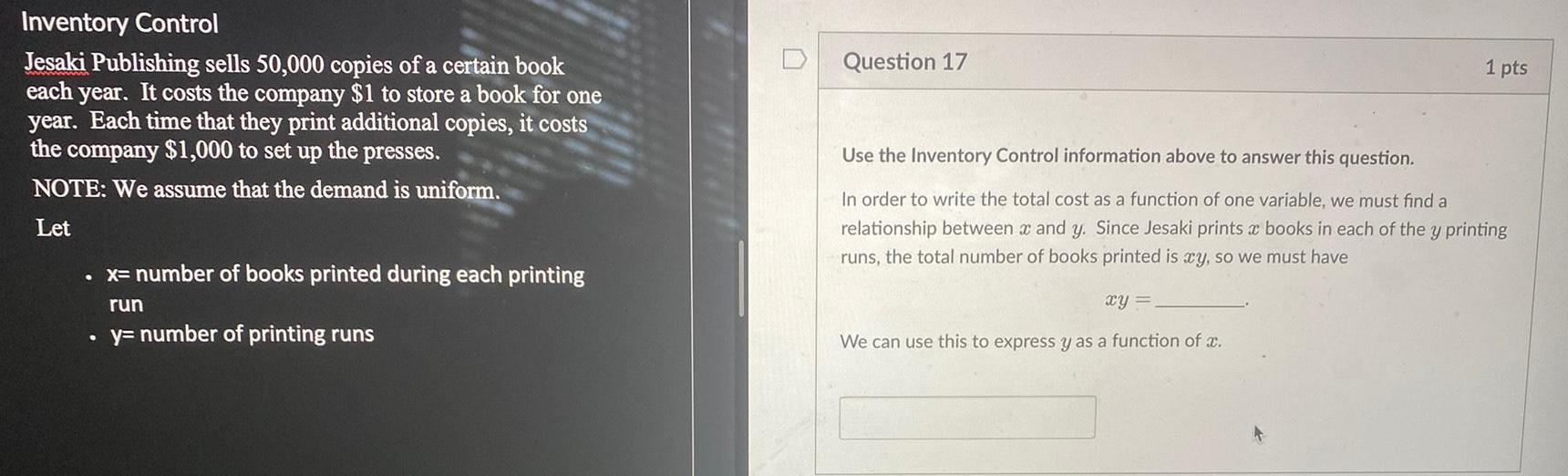
Math
Basic MathInventory Control Jesaki Publishing sells 50,000 copies of a certain book each year. It costs the company $1 to store a book for one year. Each time that they print additional copies, it costs the company $1,000 to set up the presses. NOTE: We assume that the demand is uniform. Let x= number of books printed during each printing run y= number of printing runs Use the Inventory Control information above to answer this question. In order to write the total cost as a function of one variable, we must find a relationship between x and y. Since Jesaki prints a books in each of the y printing runs, the total number of books printed is ay, so we must have
xy=
We can use this to express y as a function of a.
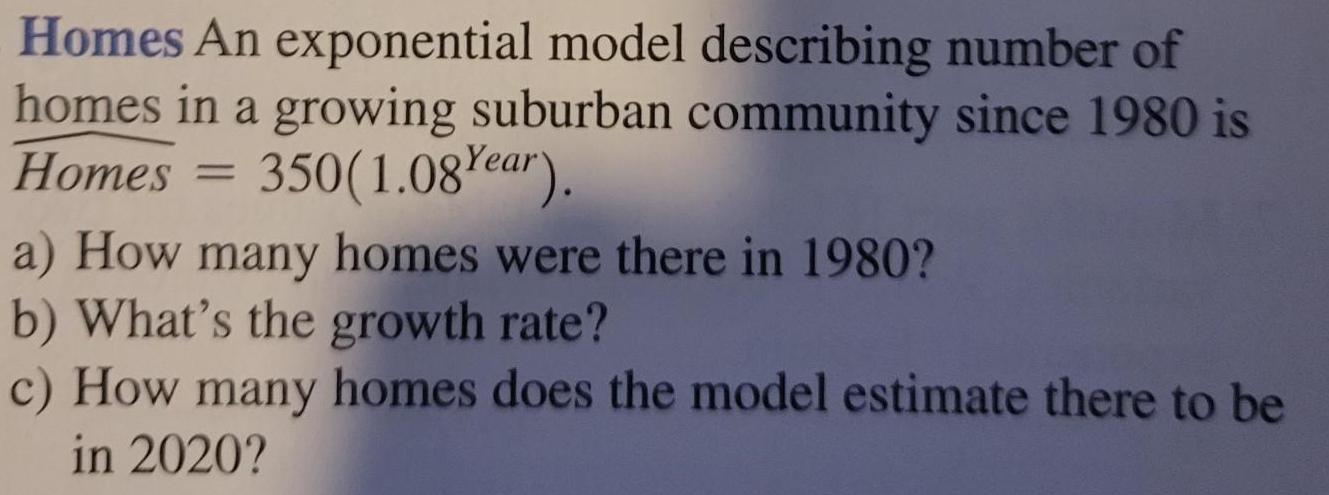
Math
Basic MathHomes An exponential model describing number of homes in a growing suburban community since 1980 is Homes = 350(1.08 Year).
a) How many homes were there in 1980?
b) What's the growth rate?
c) How many homes does the model estimate there to be in 2020?

Math
Basic MathIf a building contractor hires 8 day laborers and 1 concrete finisher, his payroll for the day is $1278. If he hires 1 day laborer and 4 concrete finishers, his daily cost is
$741. Find the daily wage for each type of worker. Solve the problem using matrices.
The daily wage for the laborer is $
The daily wage for the concrete finisher is $
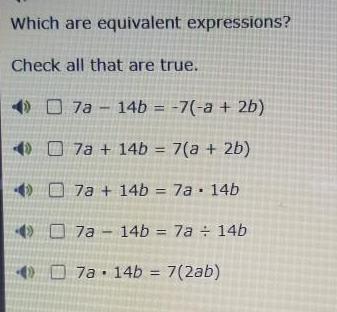
Math
Basic MathWhich are equivalent expressions?
Check all that are true.
7a - 14b = -7(-a + 2b)
7a+14b = 7(a + 2b)
47a+ 14b = 7a 14b
7a - 14b = 7a /14b
7a- 14b = 7(2ab)
Math
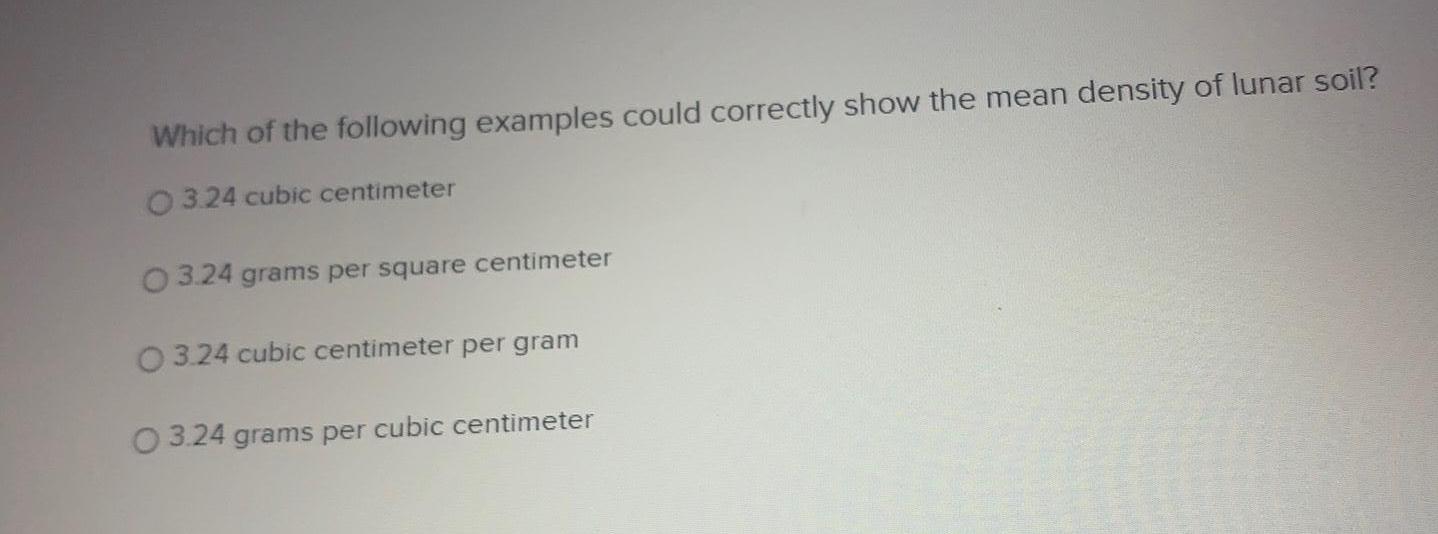
Basic MathWhich of the following examples could correctly show the mean density of lunar soil?
3.24 cubic centimeter
3.24 grams per square centimeter
3.24 cubic centimeter per gram
3.24 grams per cubic centimeter

Math
Basic MathFill in each blank with the appropriate equation. (Select all that apply.)
The two notations for the inverse of y= sin x are__and___
y = arcsin x
y = sin-¹ x
y =csc x
y=1/sin x
y = -sin x

Math
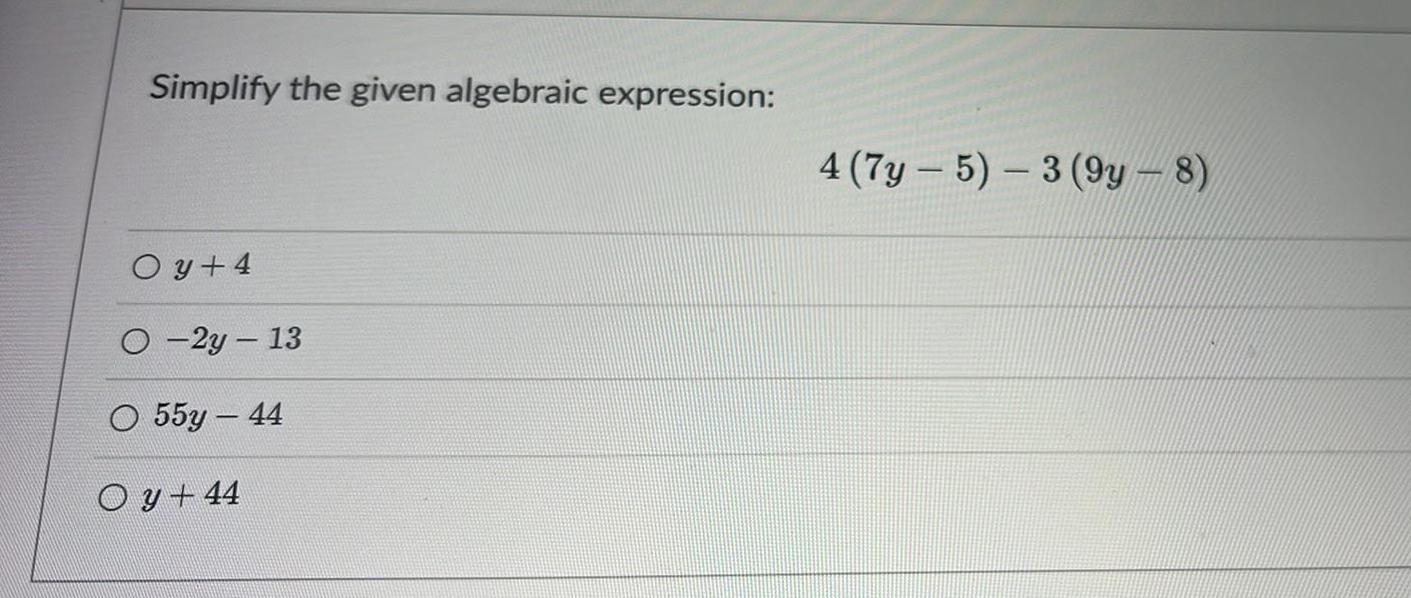
Basic MathSuppose a product's revenue function is given by R(q) = 7q² + 300q
Find an expression for the marginal revenue function, simplify it, and record your result in the box below. Be sure to use the proper variable in your answer. (Use the preview button to check your syntax before submitting your answer.)

Math
Basic MathThe length of time Joe takes to get to work varies inversely as the speed he travels. If he jogs at 6.6 feet per second it takes him 75 minutes to get to
work.
Let T = Time and V = speed:
The general equation for this variation problem is:
1) v=kT
2) T = kV
3) TV = k
4) k =v/T
(5) T=k/V

Math
Basic MathMalaya is making a collage of her birthday party photos and she wants to add an 8 x 10 inch. photo. Since there is not enough space left on the collage, she must trim the photo. If the scale factor from the original to the trimmed photo is 5:4, the new dimensions of the photo are
7x9 in
6.2 x 7.6
6.4 x 8 in
5.4 x 6.8


Math
Basic MathThe state fair is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 5 vans and 1 bus with 74 students. High School B rented and filled 13 vans and 7 buses with 386 students. Each van and each bus carried the same number of students. How many students can a van carry? How many students can a bus carry?

Math
Basic MathFind a formula for the exponential function V=h(t) that gives the value of an item initially worth $5000 that loses half its value every 8 years.
h(t) =
dollars. help (formulas) (Do not enter any commas in your formula.)
Math
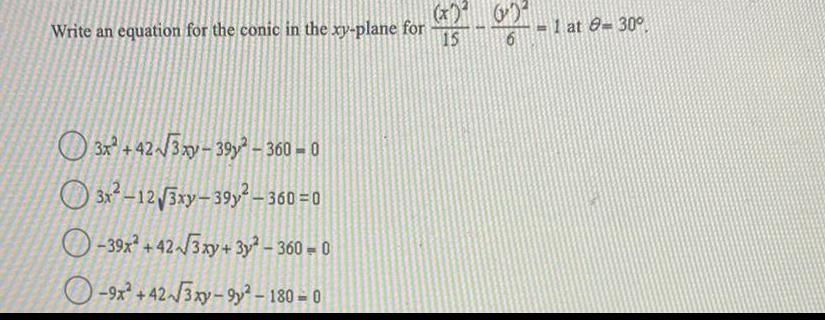
Basic MathWrite an equation for the conic in the xy-plane for (x')2 /15 - (y')^2/6 =1 at θ=30
3x+42√3xy-39y²-360 = 0
3x²-12√3xy-39y²-360=0
-39x² +42-√3xy+3y² - 360 = 0
-9x² +42-√3xy-9y2² – 180 = 0
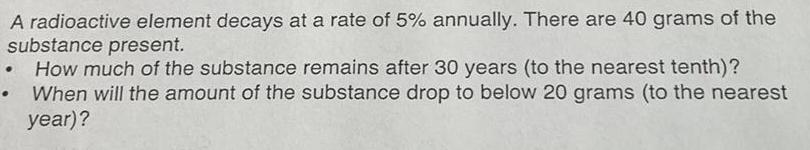
Math
Basic MathA radioactive element decays at a rate of 5% annually. There are 40 grams of the substance present.
How much of the substance remains after 30 years (to the nearest tenth)?
When will the amount of the substance drop to below 20 grams (to the nearest year)?

Math
Basic MathHow much time will be needed for $25,000 to grow to $26,015.10 if deposited at,,4% compounded quarterly? For calculating use the formula A = P(1+t/k)^kt
The amount $25,000 will grow to $26,015.10 in __ year(s).
(Do not round until the final answer. Then round to the nearest tenth as needed.)
Math
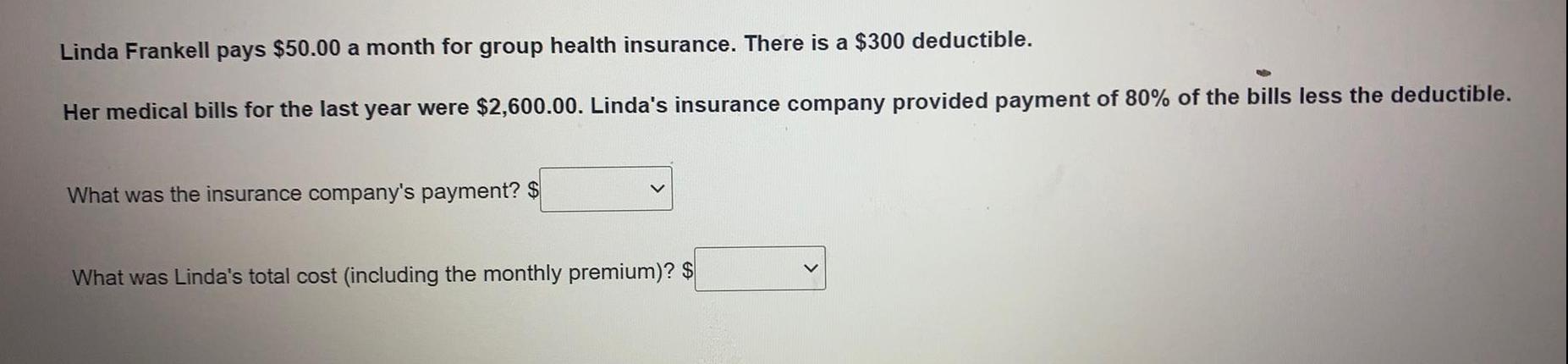
Basic MathLinda Frankell pays $50.00 a month for group health insurance. There is a $300 deductible.
Her medical bills for the last year were $2,600.00. Linda's insurance company provided payment of 80% of the bills less the deductible.
What was the insurance company's payment? $
What was Linda's total cost (including the monthly premium)? $
![Which formula would be used to calculate the middle rectangle approximation of 0∫1 4xdx using five subintervals?
M5= (0.4)[4(0.1) + 4(0.3) + 4(0.5) + 4(0.7) + 4(0.9)]
M5 = (0.2) [4(0.1) + 4(0.3) + 4(0.5) + 4(0.7) + 4(0.9)]
M5 (0.2) [4(0.2) + 4(0.4) + 4(0.6) + 4(0.8) + 4(1.0)]
M5= (0.2)[4(0.0) + 4(0.2) + 4(0.4) + 4(0.6) + 4(0.8)]](https://media.kunduz.com/media/sug-question/raw/71067631-1659115226.4116735.jpeg?w=256)
Math
Basic MathWhich formula would be used to calculate the middle rectangle approximation of 0∫1 4xdx using five subintervals?
M5= (0.4)[4(0.1) + 4(0.3) + 4(0.5) + 4(0.7) + 4(0.9)]
M5 = (0.2) [4(0.1) + 4(0.3) + 4(0.5) + 4(0.7) + 4(0.9)]
M5 (0.2) [4(0.2) + 4(0.4) + 4(0.6) + 4(0.8) + 4(1.0)]
M5= (0.2)[4(0.0) + 4(0.2) + 4(0.4) + 4(0.6) + 4(0.8)]

Math
Basic Math(a) This compound statement is made up of three simple statements. Identify them and assign a letter to each.
Choose the correct choice of statements and assignment of letters.
p: You take the product weekly.
q: You cut your calorie intake by 10%.
r: You will lose at least 10 pounds in the next 4 months.
p: A new weight loss supplement claims.
q: You take the product daily and cut your calorie intake by 10%.
r: You will lose at least 10 pounds in the next 4 months.
p: You take the product daily.
q: You cut your calorie intake by 10%.
r: You will lose at least 10 pounds in the next 4 months.
Math
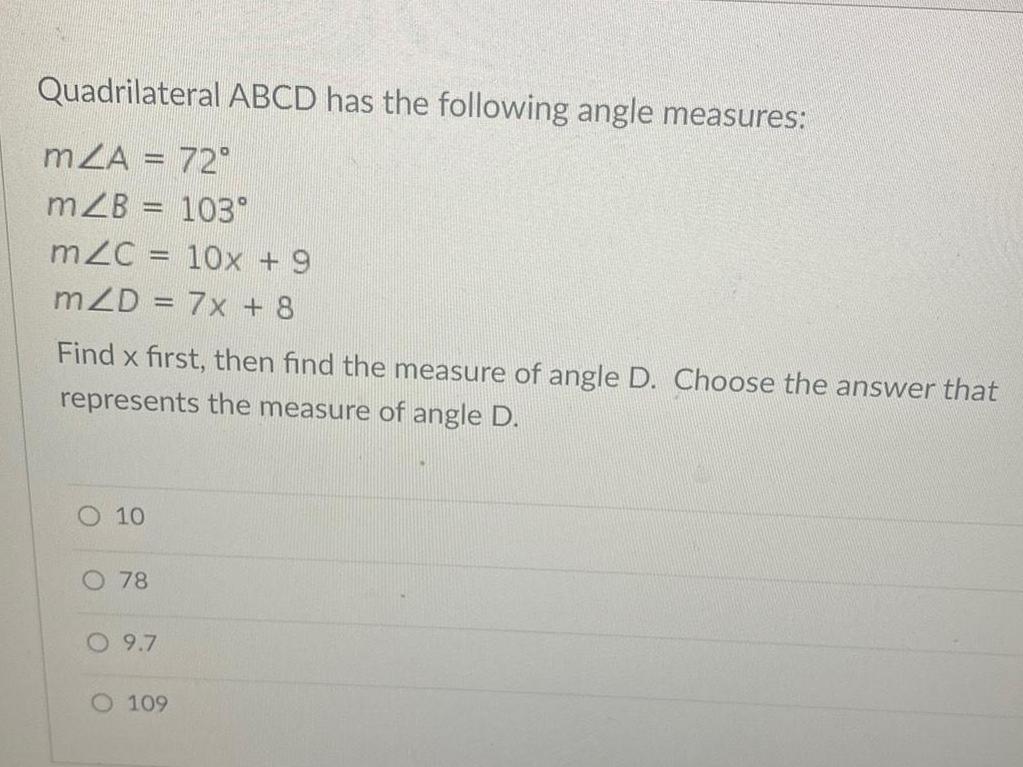
Basic MathQuadrilateral ABCD has the following angle measures:
m∠A = 72°
m∠B = 103°
m∠C= 10x + 9
m∠D = 7x + 8
Find x first, then find the measure of angle D. Choose the answer that represents the measure of angle D.
10
78
9.7
109

Math
Basic MathIn a certain lottery, 3 different numbers between 1 and 8 are drawn. These are the winning numbers. How many different selections are possible? Assume that the order in which the numbers are drawn is not important.

Math
Basic MathIn country A, about six times as many cars are manufactured per day than in country B. If the total number of these cars manufactured per day is 46,263, find the number manufactured in country B and the number manufactured in country A.
In country A,___cars are manufactured per day.
In country B,__cars are manufactured per day.

Math
Basic Math[5 pts) In a recent survey in 1050 UCLA students 175 out of the 650 female students said they preferred to drive a SUV to driving a compact car. Identify the population, sample, and variable
Population:
Sample:
Variable
is it categorical or numerical?
What percentage of female students in the study said they prefer to drive a SUV to driving a compact car? (Round answer to one decimal place)
Math
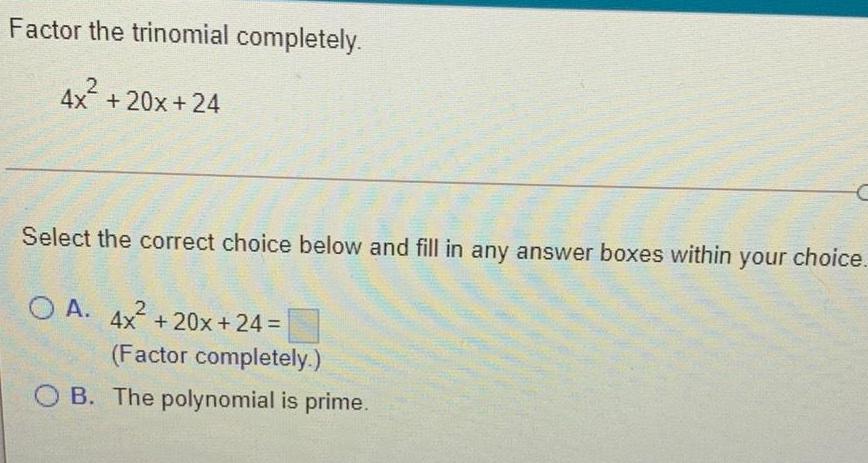
Basic MathFactor the trinomial completely.
4x² +20x+24
Select the correct choice below and fill in any answer boxes within your choice.
A. 4x² +20x + 24 =
(Factor completely.)
B. The polynomial is prime.

Math
Basic MathWater is leaking from a tank at a rate of R(t) gallons per hour, where t is time in hours. What is the meaning of R(t)dt = 2,430 in terms of the context? (1 point),
The tank is leaking at a rate of 2,430 gallons per hour from hours 2 to 4.
The tank leaked 2,430 gallons of water over the first 4 hours.
The tank leaked 2,430 gallons of water from t = 2 to t = 4.
The tank has 2,430 gallons of water left in the tank after the first 4 hours.

Math
Basic MathOutpatient surgery as a percent of total surgery at hospitals has grown. The logarithmic function f(x) = -1312+ 306 In x, where x is the number of years since 1900, is
the best-fitting logarithmic model. Use the function to estimate outpatient surgery as the percent of total surgeries in the year 1998.
What does this function estimate for the percent of outpatient surgeries in 1998?
% (Round to the nearest percent as needed.)

Math
Basic MathA particular country's exports of goods are increasing exponentially. The value of the exports, t years after 2006, can be approximated by V(t) = 1.7 e0
corresponds to 2006 and V is in billions of dollars.
a) Estimate the value of the country's exports in 2006 and 2010.
b) What is the doubling time for the value of the country's exports?
a) The value of the country's exports in 2006 is $ 1.7 billion.
(Simplify your answer. Round to the nearest tenth as needed. Do not include the $ symbol in your answer.)
The value of the country's exports in 2010 is $ billion.
(Simplify your answer. Round to the nearest tenth as needed. Do not include the $ symbol in your answer.)

Math
Basic MathThe amount of medication, in milligrams, in a patient's bloodstream after t hours, can be represented by the following function:
M(t)=75/1+ e^x+0.5
What is the rate of change for the amount of medication in the patient's bloodstream after 2 hours?
5.6894 mg/hr
-0.4316 mg/hr
-5.2578 mg/hr
-5.6894 mg/hr

Math
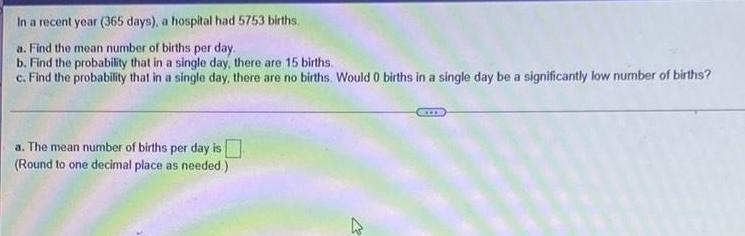
Basic MathIn a recent year (365 days), a hospital had 5753 births.
a. Find the mean number of births per day.
b. Find the probability that in a single day, there are 15 births
c. Find the probability that in a single day, there are no births. Would 0 births in a single day be a significantly low number of births?
a. The mean number of births per day is____
(Round to one decimal place as needed.)

Math
Basic MathWhich lists the possible types of roots for f(x) = 3x^4 + 7x³ + 2x² + x + 9?
One rational root and three irrational roots
Two irrational roots, one complex root, one real root
Three complex roots and one rational root
Two rational roots and two irrational roots