Basic Math Questions and Answers

Math
Basic MathWhich of the following statements is true?
A. The amplitude of f(t)= -2 sin(2t) + 2 is 1.
B. The period of g(t) =-1/2 cos(2t) is π
C. The period of h(t) = 3 tan(2t) is π/4
D. The amplitude of k(t) = -3 tan t is -3.

Math
Basic MathFor the planer curve represented by the parametric equations x = 3t and y = t^2 + 5, what is the rectangular equation of the curve?
9x² - y + 5 = 0
3y²-x+15=0
x² + y²-25= 0
x² - 9y + 45 = 0

Math
Basic MathKelly bought 4 shirts and 3 skirts for her doll and paid $11.40 total. After she did a doll fashion show for her best friend, Caitlyn wanted to know how much one of the skirts cost. Kelly remembered that each skirt cost $0.30 more than each shirt. How much did one skirt cost?
A. $1.50
B. $1.60
C. $1.65
D. $1.75
E. $1.80

Math
Basic MathThe square of a number is equal to 10 less than 7 times that number. What are the two possible solutions?
Which of the following equations is used in the process of solving this problem?
x² - 7x + 10 = 0
x² - 7x+70 = 0
x² + 7 x-10 = 0
Math
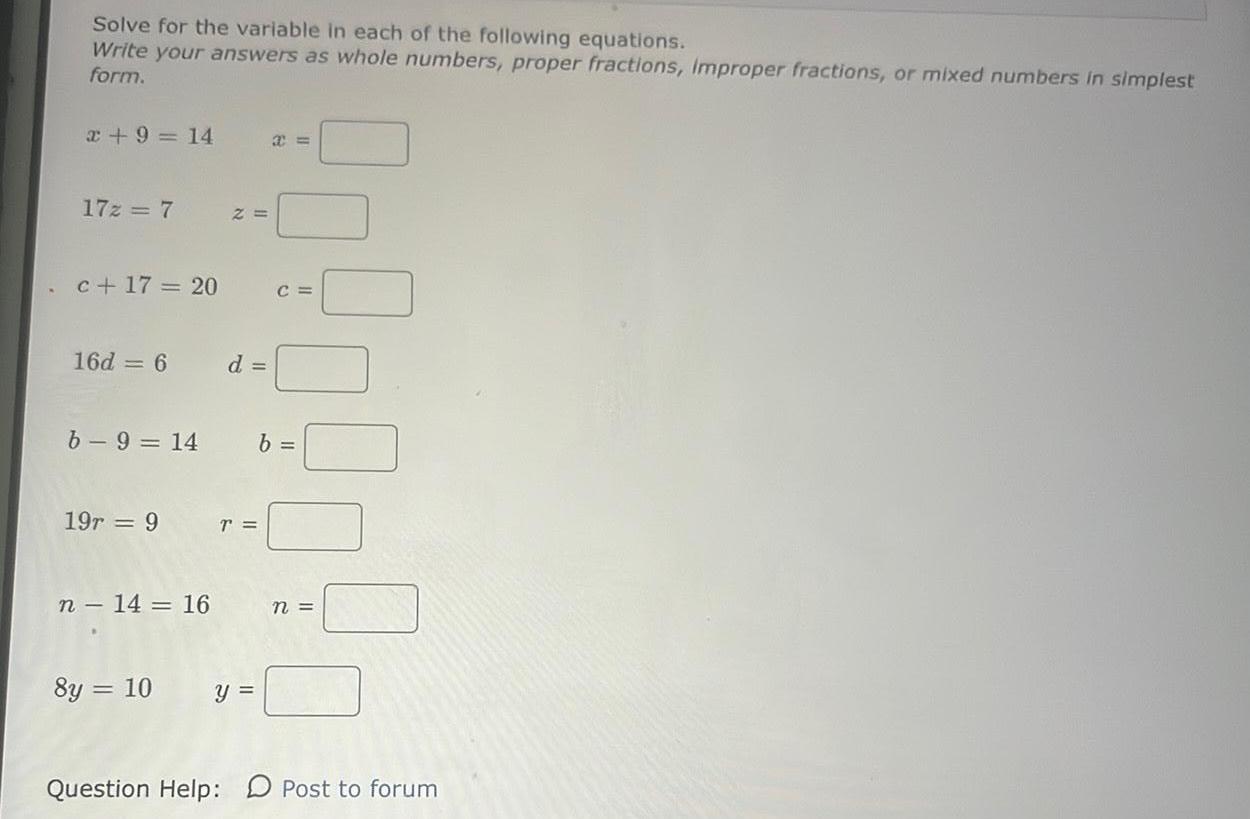
Basic MathSolve for the variable in each of the following equations.
Write your answers as whole numbers, proper fractions, Improper fractions, or mixed numbers in simplest form.
x + 9 = 14 x=
17z = 7 z=
c+ 17 = 20 c=
16d = 6 d=
b-9 = 14 b=
19r = 9 r=
n - 14 = 16 n=
8y = 10 y=

Math
Basic MathFind the probability of winning the Jackpot in a lottary if you buy just one ticket. In this lottary, a typical ticket is Formed by selecting 5 different numbers from the range {1,2,...,38}

Math
Basic MathYou had the following readings on your water meter:
December 1: 7,500 cubic feet
January 1: 7,585 cubic feet
February 1: 7,671 cubic feet
March 1: 7,749 cubic feet
What is the number of cubic feet consumed in January?

Math
Basic MathCash equivalents by definition
a. are a comparison of cash and liabilities.
b. are expected to be converted to cash within three months.
c. will be converted to cash within one year.
d. are long-term investments.

Math
Basic MathSelect the correct answer.
What is the variable being tested in an experiment?
A. control variable
B. response variable
C. placebo
D. explanatory variable
Math
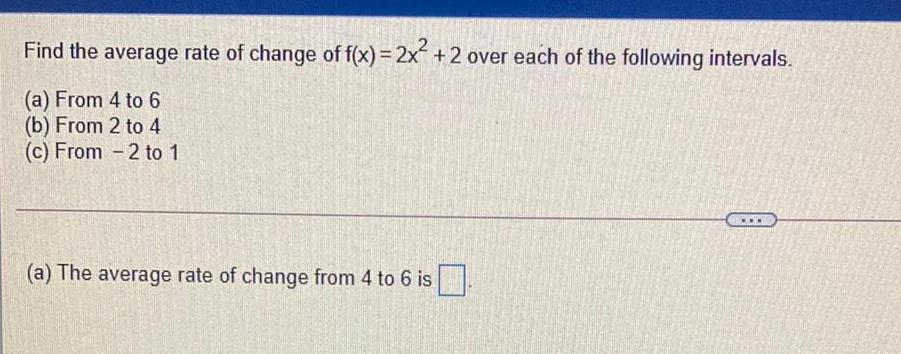
Basic MathFind the average rate of change of f(x)=2x² +2 over each of the following intervals.
(a) From 4 to 6
(b) From 2 to 4
(c) From 2 to 1
(a) The average rate of change from 4 to 6 is

Math
Basic MathThe thermal plot of a gaming system during play time is defined by 10ln(15t³) - 2T+100=T + 10t for 0<t≤ 5, where t represents time in hours and T represents temperature in °C. For which condition does the system reach a possible maximum or minimum temperature? (1 point)
30-10t=0
450t² - 10 = 0
6-90t³ = 0
15t²-10=0

Math
Basic MathThe heat loss of a glass window varies jointly as the window's area and the difference between the outside and inside temperatures. A window 2 feet by 5 feet loses 3000 Btu per hour when the temperature outside is 30° colder than the temperature inside. Find the heat loss through a glass window that is 8 feet by 15 feet when the temperature outside is 15° colder than the temperature inside.
The heat loss is ____Btu per hour.
(Type an integer or a decimal.)

Math
Basic MathStrontium-90 is a radioactive material that decays according to the function
A(t) = A e ^-0.0244t, where Ao is the initial amount present and A is the amount present at time t (in years). Assume that a scientist has a sample of 400 grams of strontium-90.
(a) What is the decay rate of strontium-90?
(b) How much strontium-90 is left after 10 years?
(c) When will only 100 grams of strontium-90 be left?
(d) What is the half-life of strontium-90?
(a) The decay rate of strontium-90 is
(Type an integer or a decimal. Include the negative sign for the decay rate.)
(b) Approximately ___grams of strontium-90 left after 10 years.
(Do not round until the final answer. Then round to the nearest whole number as needed.)
(c) Only 100 grams of strontium-90 will be left in about ____years.
(Do not round until the final answer. Then round to the nearest tenth as needed.)

Math
Basic MathFind f(g(x)) and g(f(x)) and determine whether the pair of functions f and g are inverses of each other.
f(x)=7x-4 and g(x)= x+7/4
a. f(g(x)) =
(Simplify your answer. Use integers or fractions for any numbers in the expression.)

Math
Basic MathUsing a table of values, what is an approximate solution of the given equation to the nearest quarter of a unit?
|x + 3 |= 3x + 1
A.x≈1.25
B.x≈-3.75
C.x ≈ -1.75
D.x≈1.50
Math
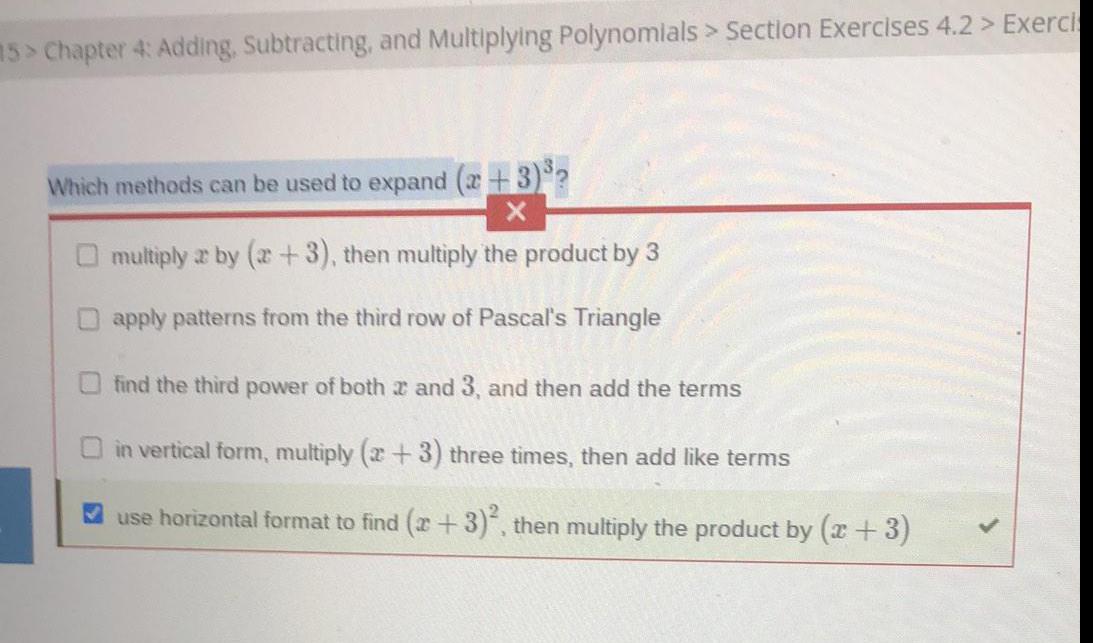
Basic MathWhich methods can be used to expand (x+3)³?
multiply 2 by (2+3), then multiply the product by 3
apply patterns from the third row of Pascal's Triangle
find the third power of both 2 and 3, and then add the terms
in vertical form, multiply (2+3) three times, then add like terms
use horizontal format to find (x+3)², then multiply the product by (x+3)

Math
Basic MathThe weight M of an object on the moon varies directly as its weight E on earth. A person who weighs 157.18 lb on earth weighs 26.72 lb on the moon. How much would a 228.24-lb person weigh on the moon?

Math
Basic MathLet a curve be defined as siny = x + y. Determine which of the following statement(s) is/are true. (1 point)
I. The curve has a vertical tangent when cosy - 1 = 0.
II. The curve has no horizontal tangents because cosy - 1 * 0.
III. The curve has no horizontal tangents because dy/dx≠0.
I only
III only
I and III
I and II

Math
Basic MathA rope from the top of a mast on a sailboat is attached to a point 19 feet from the mast. If the rope is 28 feet long, how tall is the mast? Round to the nearest tenth of a foot.

Math
Basic MathOfficials begin to release water from a full man-made lake at a rate that would empty the lake in 6 weeks, but a river that can fill the lake in 15 weeks is replenishing the lake at the same time. How many weeks does it take to empty the lake? Express your answer as a fraction reduced to lowest terms, if needed.

Math
Basic MathDuring the past six months, 73.2 percent of U.S. households purchased sugar. Assume that these expenditures are approximately normally distributed with a mean of $8.22 and a standard deviation of $1.10. Find the probability that a household spent more than $10.00 on sugar.
Multiple Choice
.7320
.9474
.0528
.2680

Math
Basic MathThe Pool Fun Company has learned that, by pricing a newly released Fun Noodle at $3, sales will reach 9000 Fun Noodles per day during the summer. Raising the price to $4 will cause the sales to fall to 5000 Fun Noodles per day.
a. Assume that the relationship between sales price, x, and number of Fun Noodles sold, y, is linear. Write an equation in slope-intercept form describing this relationship. Use ordered pairs of the
form (sales price, number sold).
The equation is y=-4000x+21000. (Type your answer in slope-intercept form.)
b. Predict the daily sales of Fun Noodles if the price is $3.50.
sales

Math
Basic MathCompany XYZ has 34 employees in the Finance Department, 45 technicians, and 32 in the Engineering Department. The HR Department received 20 complaints from the whole company. There were 5 complaints from the technicians and 3 from the Finance Department. There were 7 complaints from the Engineering Department.
What percent of complaints came from either the technicians or the Finance Department?
![A manufacturer of personal computers tests competing brands and finds that the amount of energy they require is normally distributed with a mean of 285 kwh and a standard deviation of 9.1 kwh. If the lowest 25 percent and the highest 30 percent are not included in a second round of tests, what are the upper and lower limits for the energy amounts of the remaining computers?
Multiple Choice
[269.76, 300.24]
[278.86, 289.78]
[280.22, 289.78]
[280.22, 300.24]](https://media.kunduz.com/media/sug-question/raw/68680640-1659101641.4983642.jpeg?w=256)
Math
Basic MathA manufacturer of personal computers tests competing brands and finds that the amount of energy they require is normally distributed with a mean of 285 kwh and a standard deviation of 9.1 kwh. If the lowest 25 percent and the highest 30 percent are not included in a second round of tests, what are the upper and lower limits for the energy amounts of the remaining computers?
Multiple Choice
[269.76, 300.24]
[278.86, 289.78]
[280.22, 289.78]
[280.22, 300.24]
Math
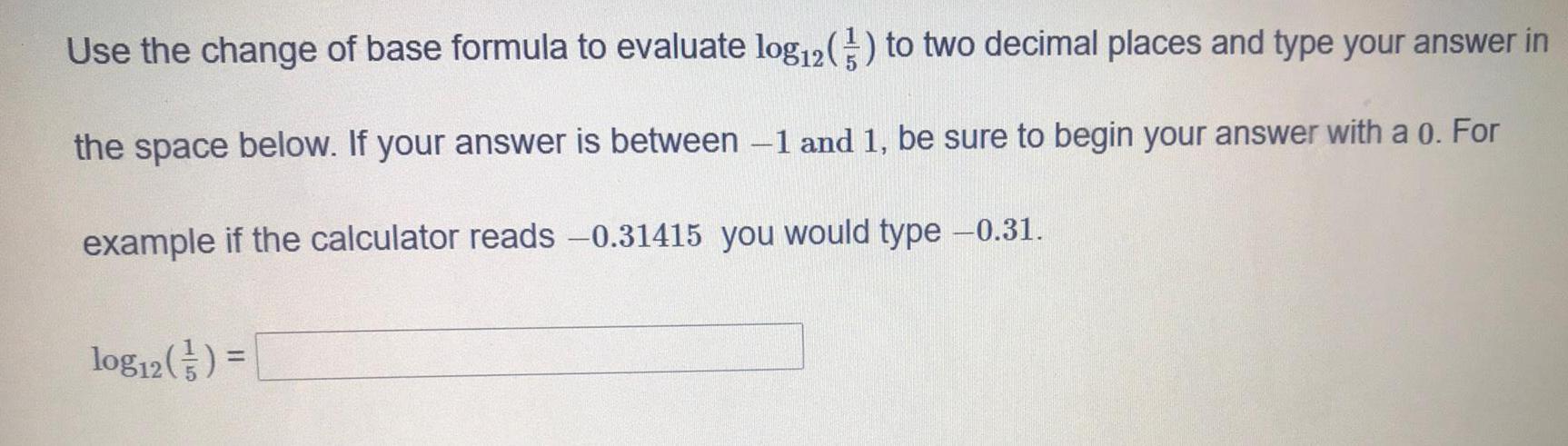
Basic MathUse the change of base formula to evaluate log12(1/5) to two decimal places and type your answer in the space below. If your answer is between -1 and 1, be sure to begin your answer with a0. For example if the calculator reads -0.31415 you would type -0.31.
log12(1/5)=___

Math
Basic MathAssume that a rectangle with sides x and y is expanding with time. Let y=2x and
x(t)=3t+1. What is the formula for the rate of change of the area with respect to time?
dA/dt=12(3t-1)
dA/dt=(3t+1)
dA/dt=4(3t - 1)
dA/dt=12(3t+1)
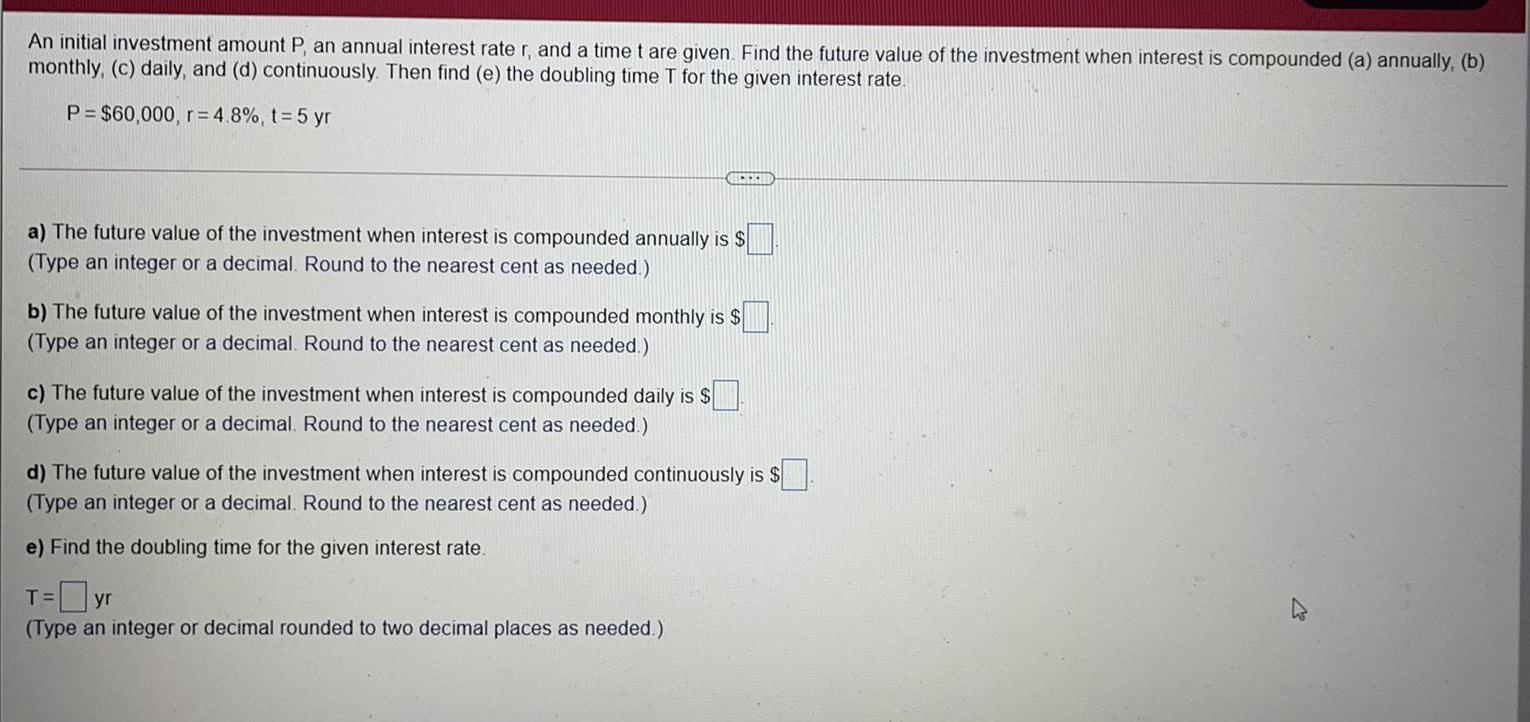
Math
Basic MathAn initial investment amount P, an annual interest rate r, and a time t are given. Find the future value of the investment when interest is compounded (a) annually, (b)
monthly, (c) daily, and (d) continuously. Then find (e) the doubling time T for the given interest rate.
P = $60,000, r=4.8%, t = 5 yr
a) The future value of the investment when interest is compounded annually is $
(Type an integer or a decimal. Round to the nearest cent as needed.)
b) The future value of the investment when interest is compounded monthly is $
(Type an integer or a decimal. Round to the nearest cent as needed.)
c) The future value of the investment when interest is compounded daily is $
(Type an integer or a decimal. Round to the nearest cent as needed.)
d) The future value of the investment when interest is compounded continuously is $.
(Type an integer or a decimal. Round to the nearest cent as needed.)
e) Find the doubling time for the given interest rate.
T = yr
(Type an integer or decimal rounded to two decimal places as needed.)

Math
Basic MathThe total number of public electric charging units available for hybrid vehicles has increased exponentially since 2006. The number of outlets A(t) at these alternative fueling stations t years after 2006 can be approximated by A(t) = 224(2.69), where t= 0 corresponds to 2006. How many outlets were available in 2008, in 2010, in 2011?
The number of outlets available in the year 2008 was approximately
(Simplify your answer. Round to the nearest integer as needed.)

Math
Basic MathAssume that 75% of people are left-handed. If we select 5 people at random, find the
probability of each outcome described below, rounded to four decimal places:
a. There are some lefties (≥1) among the 5 people. 0.9990
b. There are exactly 3 lefties in the group. 0.2637
c. There are at least 4 lefties in the group. 0.6328
d. There are no more than 2 lefties in the group. 0.1035
e. How many lefties do you expect? 3.75
f. With what standard deviation?
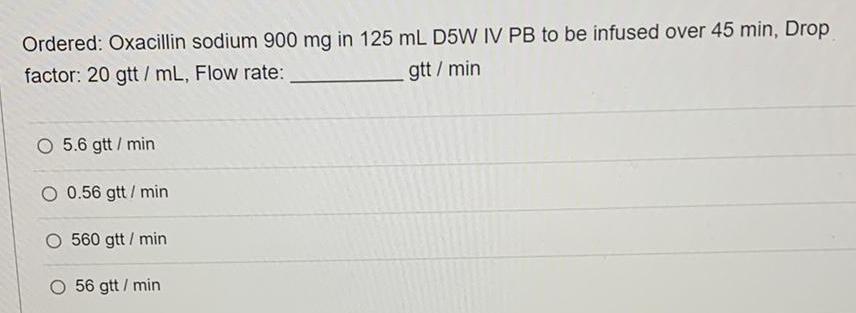
Math
Basic MathOrdered: Oxacillin sodium 900 mg in 125 mL D5W IV PB to be infused over 45 min, Drop factor: 20 gtt/mL, Flow rate: gtt / min
5.6 gtt / min
0.56 gtt / min
560 gtt / min
56 gtt / min

Math
Basic MathAllison buys a spool of thread for sewing. There are 8 yards of thread on the spool. She uses 2 meters. How much thread is left on the spool in meters? Round your answer to the nearest thousandth, if necessary.

Math
Basic MathCalculate the scaling factor that will adjust the recipe to produce the desired yield. (Round to 2 decimal places). Recipe Yield 12 6-oz crabs Desired Yield 50 2-oz crab cake).Scaling factor is
Maximum number of characters (including HTML tags added by text editor): 32,000
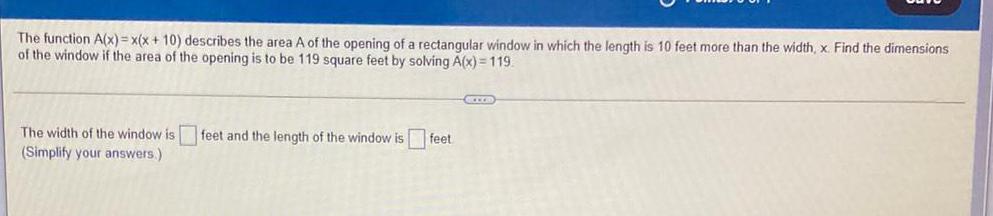
Math
Basic MathThe function A(x)= x(x + 10) describes the area A of the opening of a rectangular window in which the length is 10 feet more than the width, x. Find the dimensions of the window if the area of the opening is to be 119 square feet by solving A(x) = 119
The width of the window is feet and the length of the window is feet (Simplify your answers.)
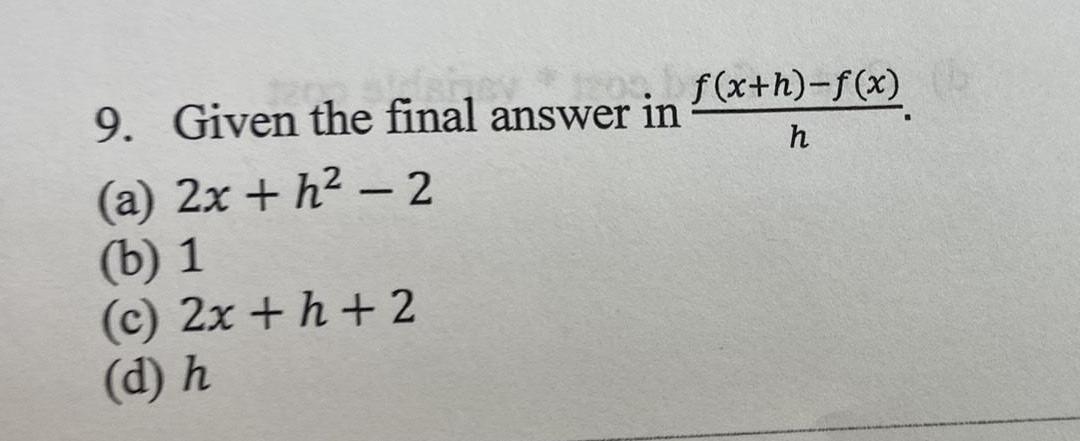
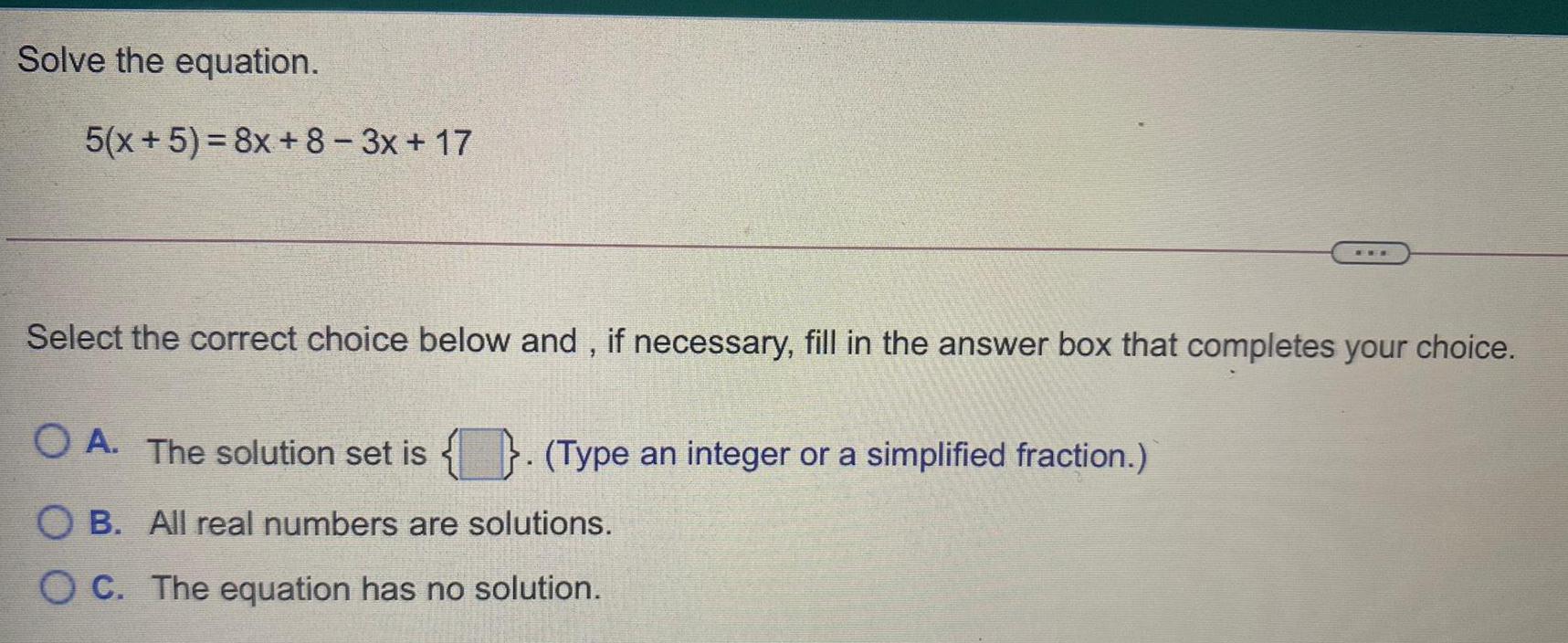
Math
Basic MathSolve the equation.
5(x+5)=8x+8-3x+17
Select the correct choice below and, if necessary, fill in the answer box that completes your choice.
OA. The solution set is { }. (Type an integer or a simplified fraction.)
OB. All real numbers are solutions.
OC. The equation has no solution.

Math
Basic MathThe total numbers of Navy personnel N (in thousands) and Marines personnel M (in thousands) from 2000 through 2007 can be approximated by the models
N(t)=0.194³-7.88+2+12.9t+375 and M(t) = 0.031³-0.25t² +6.7t+173
where t represents the year, with t = 0 corresponding to 2000.
Find and interpret (N-M)(t).
(N-M)(t) = 0.163+³+7.632-6.2t+202, which represents the difference between the number of Navy personnel and the number of Marines personnel.
(N-M)(t) = 0.163³-7.632-6.2t-202, which represents the difference between the number of Navy personnel and the number of Marines personnel.
(N-M)(t) = 0.163³ +7.632 +6.2t+202, which represents the difference between the number of Navy personnel and the number of Marines personnel.
(N-M) (t) = 0.163³-7.63²-6.2t+202, which represents the difference between the number of Navy personnel and the number of Marines personnel.
(N-M)(t) = 0.163³-7.632 +6.2t+202, which represents the difference between the number of Navy personnel and the number of Marines personnel.

Math
Basic MathSolve the following equation using a graphical method.
12x-16-41-7x
x=
Type an integer or a simplified fraction.)

Math
Basic MathA rectangle has a width of x centimeters and a length that is 10 centimeters longer than its width. If the total perimeter is 220 centimeters, what is the measure of the width?
40 centimeters
200 centimeters
50 centimeters
4 centimeters

Math
Basic MathA town has a population of 14000 and grows at 3.5% every year. What will be the
population after 14 years, to the nearest whole number?
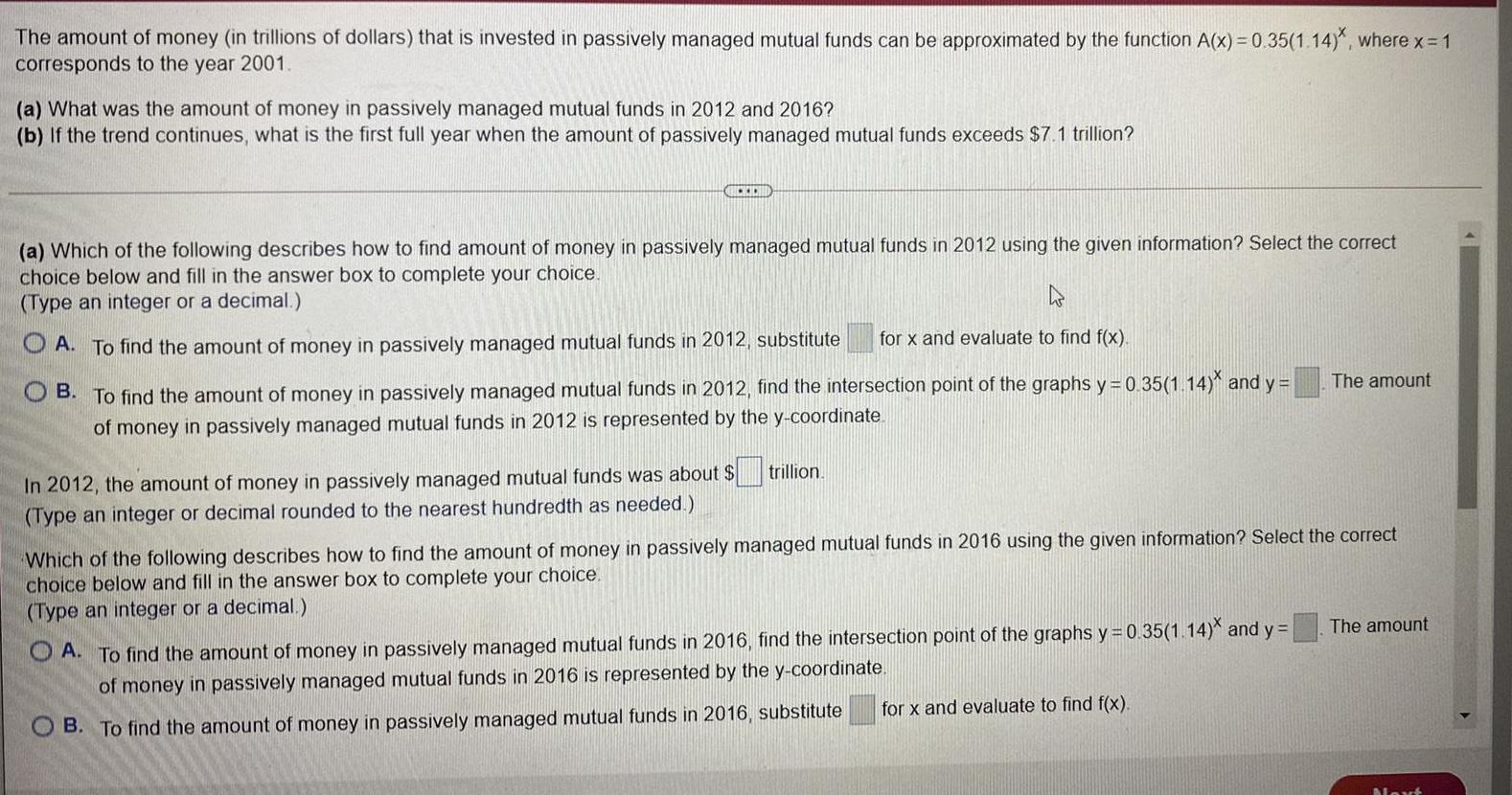
Math
Basic MathThe amount of money (in trillions of dollars) that is invested in passively managed mutual funds can be approximated by the function A(x) = 0.35(1.14)*, where x = 1
corresponds to the year 2001.
(a) What was the amount of money in passively managed mutual funds in 2012 and 2016?
(b) If the trend continues, what is the first full year when the amount of passively managed mutual funds exceeds $7.1 trillion?
(a) Which of the following describes how to find amount of money in passively managed mutual funds in 2012 using the given information? Select the correct
choice below and fill in the answer box to complete your choice.
(Type an integer or a decimal.)
A. To find the amount of money in passively managed mutual funds in 2012, substitute
for x and evaluate to find f(x).
B. To find the amount of money in passively managed mutual funds in 2012, find the intersection point of the graphs y = 0.35(1.14) and y =
of money in passively managed mutual funds in 2012 is represented by the y-coordinate
In 2012, the amount of money in passively managed mutual funds was about $
(Type an integer or decimal rounded to the nearest hundredth as needed.)
trillion.
Which of the following describes how to find the amount of money in passively managed mutual funds in 2016 using the given information? Select the correct
choice below and fill in the answer box to complete your choice.
(Type an integer or a decimal.)
A. To find the amount of money in passively managed mutual funds in 2016, find the intersection point of the graphs y = 0.35(1.14)* and y=
of money in passively managed mutual funds in 2016 is represented by the y-coordinate.
B. To find the amount of money in passively managed mutual funds in 2016, substitute for x and evaluate to find f(x).
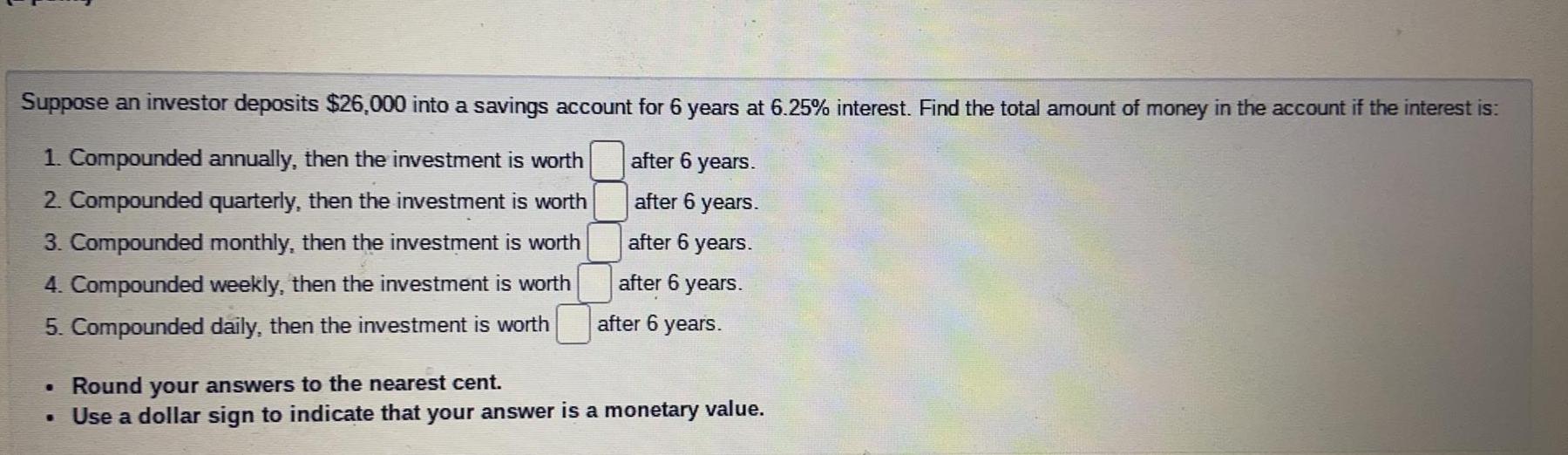
Math
Basic MathSuppose an investor deposits $26,000 into a savings account for 6 years at 6.25% interest. Find the total amount of money in the account if the interest is:
1. Compounded annually, then the investment is worth __ after 6 years.
2. Compounded quarterly, then the investment is worth __ after 6 years.
3. Compounded monthly, then the investment is worth __ after 6 years.
4. Compounded weekly, then the investment is worth __ after 6 years.
5. Compounded daily, then the investment is worth __ after 6 years.
• Round your answers to the nearest cent.
• Use a dollar sign to indicate that your answer is a monetary value.


Math
Basic MathThe solution of differential equation y1y3 = 3y2² is (where a, b, c are arbitrary constants & yn denotes nth derivative of y w rt'x
O x = ay² + by + c
O y = ax² + bx + c
O y = ae^x + be-^x +c
O x = ae^y + be^-y+c

Math
Basic Matha. Find the linear approximating polynomial for the following function centered at the given point a.
b. Find the quadratic approximating polynomial for the following function centered at the given point a.
c. Use the polynomials obtained in parts a. and b. to approximate the given quantity.
f(x) = -1/x, a=1 approximate -1/1.05
a. p₁ (x) =

Math
Basic MathConsider the set of real numbers: {x| -1 < x ≤0}.
Graph the set of numbers on the real number line.

Math
Basic MathDuring the 2005 football season, Team Tackle beat Team Sack by 15 points. If their combined scores totaled 39, find the individual team scores.
Team Tackle's score was points.

Math
Basic Math12.Identify the hypothesis and conclusion of this conditional statement:
If two lines intersect at right angles, then the two lines are perpendicular.
a.Hypothesis: The two lines are perpendicular.
Conclusion: Two lines intersect at right angles.
b.Hypothesis: Two lines intersect at right angles.
Conclusion: The two lines are perpendicular.
c.Hypothesis: The two lines are not perpendicular.
Conclusion: Two lines intersect at right angles.
d.Hypothesis: Two lines intersect at right angles.
Conclusion: The two lines are not perpendicular.
A
B
C
D

Math
Basic MathEach baseball team has nine players and each football team has eleven players. Five schools have both baseball and football teams. Three schools have only a baseball team. How many players are there for all eight schools?

Math
Basic MathYesterday, Martina went on a bike ride. Her average speed was 10 miles per hour. Today, she went on another ride, this time averaging 12 miles per hour. In the two days, she biked for a combined total time of 10 hours.
Let x be the number of hours she biked yesterday. Write an expression for the combined total number of miles she biked in the two days.

Math
Basic MathThe revenue function R(x) and the cost function C(x) for a particular product are given. These functions are valid only for the specified range of values. Find the number of units that must be produced to break even
R(x)=200x-x², C(x)=25x+6250, 0≤x≤ 100
The manufacturer must produce units to break even.