Differentiation Questions and Answers
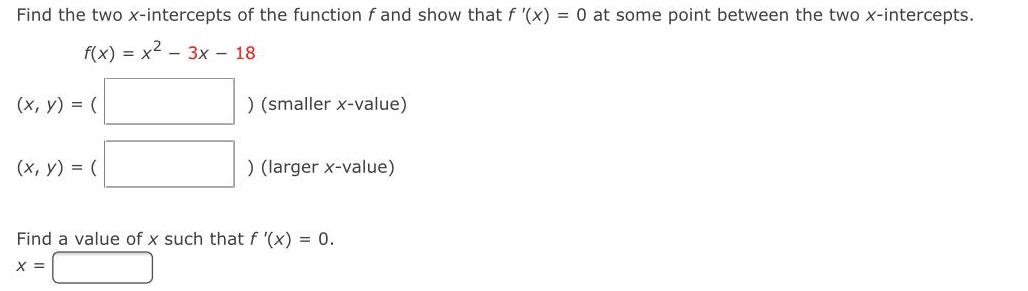
Math
DifferentiationFind the two x-intercepts of the function f and show that f '(x) = 0 at some point between the two x-intercepts.
f(x)=x²-3x - 18
(x, y) = () (smaller x-value)
(x, y) = () (larger x-value)
Find a value of x such that f '(x) = 0.
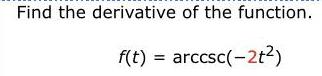

Math
DifferentiationFind the critical numbers of the function.
f(x) = 5x² - 4x
Step 1
To find the critical numbers of f, you must find all x-values for which f'(x) or f'(x)

Math
DifferentiationThe minimum and maximum of a function on an interval are the extreme values, or extrema (the singular
form of extrema is extremum), of the function on the interval. In the given problem, the extremum occurs
when x =
The specified function is f(x) = -3x√√x + 2 = −3x(x + 2)1/2.
Differentiate f(x) using the product rule.
f'(x) = -3x (x + 2)
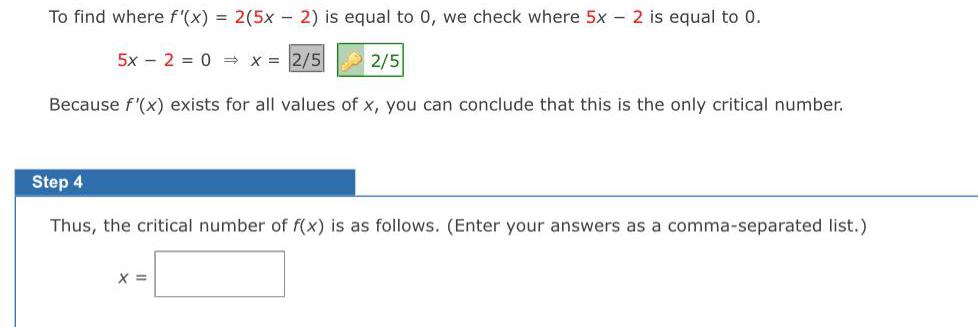
Math
DifferentiationTo find where f'(x) = 2(5x - 2) is equal to 0, we check where 5x 2 is equal to 0.
5x − 2 = 0 x =
Because f'(x) exists for all values of x, you can conclude that this is the only critical number.
Thus, the critical number of f(x) is as follows. (Enter your answers as a comma-separated list.)
X =
![Find dy/dx by implicit differentiation.
x4 + 5 = 15
With implicit differentiation, we differentiate all the terms in our equation with respect to x. Keep in mind we are implying that y is a function of x. Think of it as y(x). In order to differentiate it, we will need to use the Chain Rule.
To start, differentiate both sides of the equation with respect to x.
x4 + y5= 15
d/dx [x4] +d/dx [y5] =d/dx [15]
x+d/dx[y5]=](https://media.kunduz.com/media/sug-question/raw/54203657-1658003388.047396.jpeg?w=256)
Math
DifferentiationFind dy/dx by implicit differentiation.
x4 + 5 = 15
With implicit differentiation, we differentiate all the terms in our equation with respect to x. Keep in mind we are implying that y is a function of x. Think of it as y(x). In order to differentiate it, we will need to use the Chain Rule.
To start, differentiate both sides of the equation with respect to x.
x4 + y5= 15
d/dx [x4] +d/dx [y5] =d/dx [15]
x+d/dx[y5]=
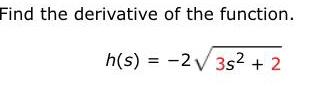

Math
DifferentiationFind an equation of the tangent line to the graph of the equation at the given point.
(-2, 1)
x² + x arctan y = y - 1,
Step 1
Use implicit differentiation to find y'.
2x +
x² + x arctan y = y - 1,
+
X
1 + y²
-y' = y'
(₁ - 12) =
(1.
1+
y'
![To find the derivative of the left side of the equation, rewrite the square root using exponents and use the
Power Rule. Use the Sum Rule and the Constant Multiple Rule to solve the right side.
dx
d
k√x]= = dx
d
-kx
dx
SNA
1/2
-[3x + 12]
d
= dx
= 3
3x +
dx
12](https://media.kunduz.com/media/sug-question/raw/54176601-1658000844.8882222.jpeg?w=256)
Math
DifferentiationTo find the derivative of the left side of the equation, rewrite the square root using exponents and use the
Power Rule. Use the Sum Rule and the Constant Multiple Rule to solve the right side.
dx
d
k√x]= = dx
d
-kx
dx
SNA
1/2
-[3x + 12]
d
= dx
= 3
3x +
dx
12
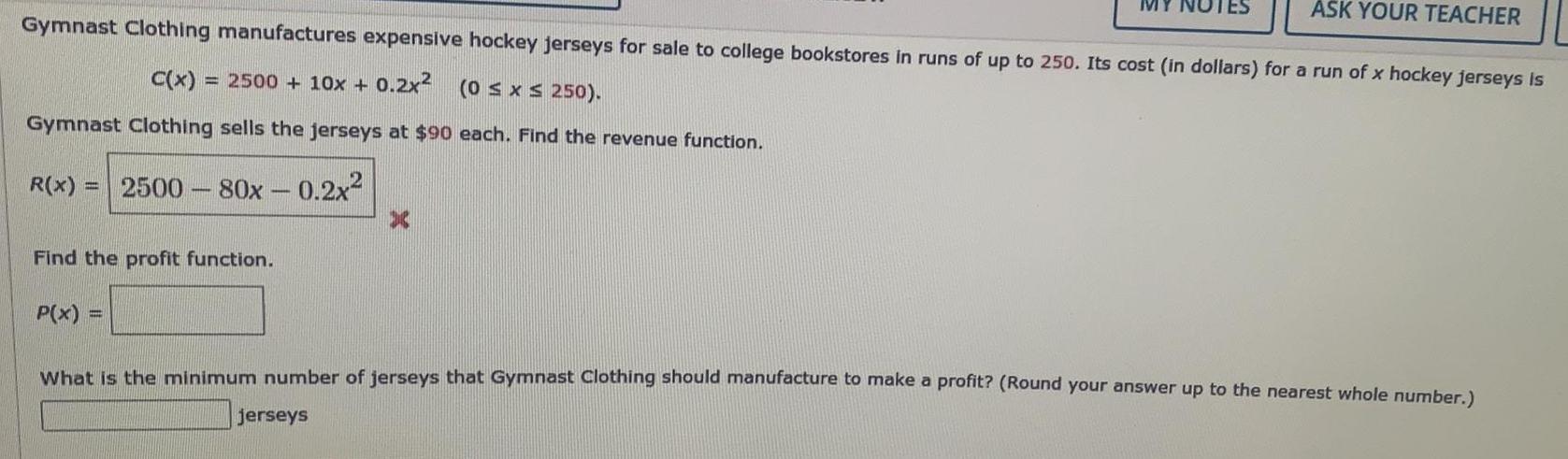
Math
DifferentiationASK YOUR TEACHER
Gymnast Clothing manufactures expensive hockey jerseys for sale to college bookstores in runs of up to 250. Its cost (in dollars) for a run of x hockey jerseys is
C(x) = 2500 + 10x + 0.2x² (0 ≤ x ≤ 250).
Gymnast Clothing sells the jerseys at $90 each. Find the revenue function.
R(x) = 2500 - 80x
0.2x²
Find the profit function.
P(x) F
What is the minimum number of jerseys that Gymnast Clothing should manufacture to make a profit? (Round your answer up to the nearest whole number.)
jerseys

Math
DifferentiationExxon/Mobil scientists flew over an ocean oil spill that looked like a large circular disc.
At that time, they estimated the diameter at 80 meters. The radius of the spill was
growing at the rate of 7 meters per hour. Make a table to show the area of the circular
spill each hour from the time of the flight. Write an equation for a function that
represents the area of the oil spill based on the number of hours that have passed since
'the fly-over.
a.
How big will the spill be after 24 hours?
About how many days will it take for the spill to cover an area of 10
square kilometers?
b.

Math
DifferentiationThe demand function p = D(x) = -0.2x +39 and the total cost function C(x) = 1.3x2 +8.4x+65 for a particular commodity are given in terms of the level of production x.
a. Find the revenue R(x) and profit P(x).
b. Find all values of x for which production of the commodity is profitable.
a. R(x) = -0.2x² + 39x; P(x) = -1.5x² + 30.6x - 65
b. 2.41 < x < 17.99
a. R(x) = -0.2x² + 39; P(x) = -1.5x² + 30.6x - 65
b. x > 2.41
a. R(x) = -0.2x² + 39x; P(x) = 1.5x² - 30.6x + 65
b. x > 2.41
a. R(x) = -0.2x² + 39: P(x) = 1.5x² - 30.6x + 65
b. 2.41 < x < 17.99

Math
DifferentiationFind the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
Function
f(x) =8/x²
Point
(2, 2)

Math
DifferentiationAn object is moving along a horizontal coordinate line according to the formula s=t^3-12t^2+21t, where s, the directed distance from the origin, is in feet and 1 is in seconds
(a) What are v(t) and a(t), the velocity and acceleration at time 1?
(b) When is the object moving to the right?
(c) When is the object moving to the left?
(d) When is its acceleration negative?

Math
DifferentiationFind the instantaneous rate of change of the position function y = f(t) in feet at the given time t in seconds.
f(t)=6t+ 2/t, t = 7
The instantaneous rate of change of f(t) at t = 7 is

Math
DifferentiationFind the derivative of the function f by using the rules of differentiation.
f(r) = 4πr3/3

Math
Differentiation2. For rational functions, we can evaluate "end behavior" by observing the highest
power of x in the numerator and in the denominator. The other terms will literally
be over-powered by the term with the highest power. You can discard the terms of
lower power and focus on only the highest power for evaluating end behavior.
2x³+4x²-5
a) f(x)= 5x³-10x
Then consider the same as above:
f(x) →
f(x) →
as xx
Can you identify the vertical asymptote(s)?
as x-
4
b) g(x)=**-x³-1-
2x³ + x
Then consider the same as above:
8(x) →
as x->>0
8(x) →
as x->-00
Can you identify the vertical
asymptote(s)?
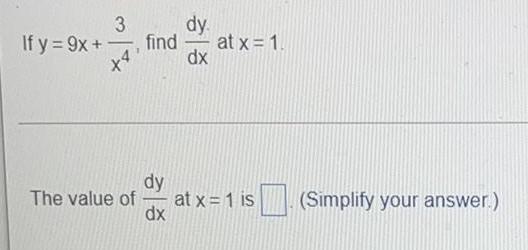
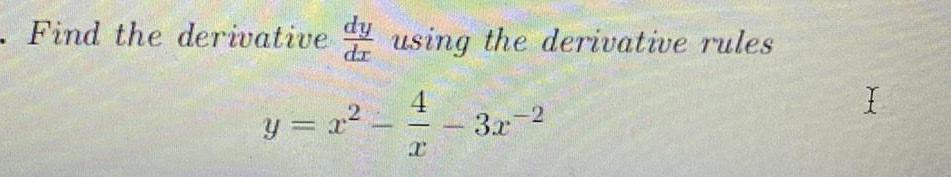

Math
DifferentiationUse the four-step process to find r'(x) and then find r'(1), r'(2), and r'(3).
r(x) = 9+4x²

Math
DifferentiationA lottery game requires that 3 different numbers are picked from 1 to 12. If someone picks all 3 winning numbers, the person wins $12 million Complete parts (a) and (b) below.
(a) How many ways are there to choose 3 numbers if order is not important?
There are ways to choose the numbers.
(Type a whole number.)
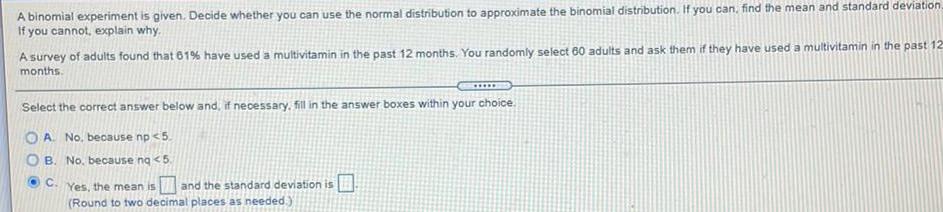
Math
DifferentiationA binomial experiment is given. Decide whether you can use the normal distribution to approximate the binomial distribution. If you can, find the mean and standard deviation. If you cannot, explain why.
A survey of adults found that 61% have used a multivitamin in the past 12 months. You randomly select 60 adults and ask them if they have used a multivitamin in the past 12
months.
Select the correct answer below and, if necessary, fill in the answer boxes within your choice.
A. No, because np <5.
B. No. because ng <5.
C. Yes, the mean is and the standard deviation is

Math
DifferentiationConsider the curve given by the parametric equations z = sint, y = sin(t + sint) where -∞ < t < ∞. Note that it has two tangents at the origin (0,0) since both t = 0 and t = π corresond to the origin. Find the equations of the two tangents to the curve at the origin.

Math
DifferentiationThe volume of a box is modeled by the function V(h)=4h³ - 24h² + 35h, where h represents the height of the box and V represents the volume of the box. What approximate height maximizes the volume of the box?
15.02
2.5
0.95
3.5

Math
DifferentiationA Spherical balloon is being inflated.
Find a general formula for the instantaneous rate of change of the volume V with respect to the radius r. given that V = 4².
Answer:
Find the rate of change of V with respect to r at the instant when the radius is r = 5.
Answer:

Math
DifferentiationCalculate the derivative of the function:
f(x) = In ((x + 2)^6x^4(x-5)^8)
Note that this is not quite logarithmic differentiation since the log function is already there in front. But you can still use the log laws to first simplify the
expression before differentiating.
f'(x) =
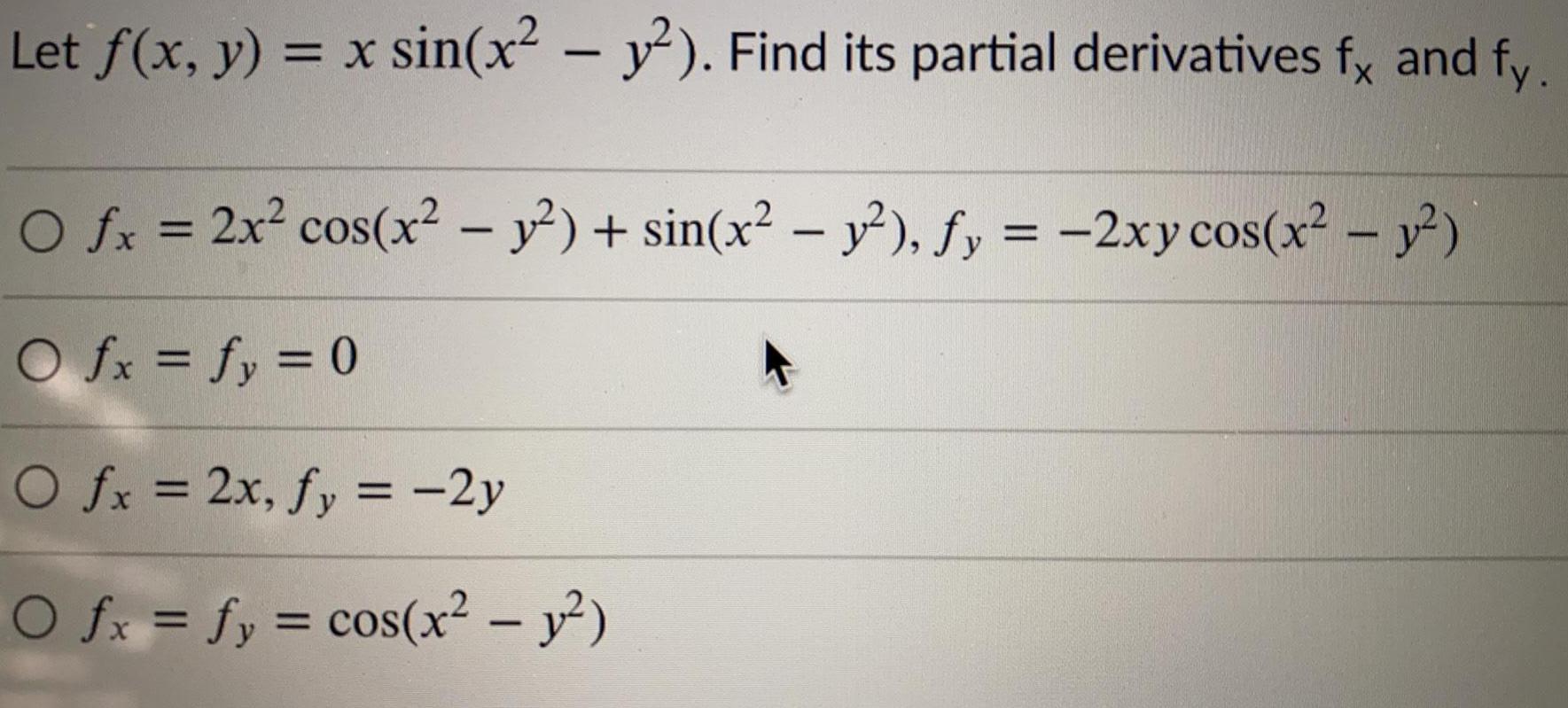
Math
DifferentiationLet f(x, y) = x sin(x² - y²). Find its partial derivatives fx and fy.
fx = 2x² cos(x² - y²) + sin(x² - y²), fy = -2xy cos(x² - y²)
fx = fy = 0
fx = 2x, fy = -2y
fx = fy = cos(x² - y²)

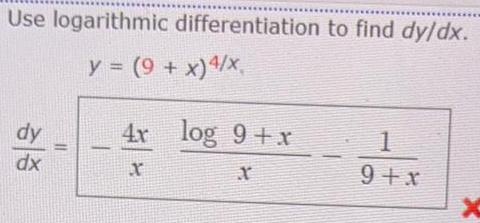
Math
DifferentiationUse logarithmic differentiation to find dy/dx.
y = (9 + x) 4/x
dy
dx
4x log 9+x
X
1
9+x


Math
DifferentiationIn the equation, x and y are functions of t. Differentiate with respect to t to find a relation between dx/dt and dy/dt.
x² + xy = y²

Math
DifferentiationSuppose a product's revenue function is given by R(q) = 2q² + 900g, where R(q) is in dollars
and q is units sold.
Find a numeric value for the marginal revenue at 143 units, and record your result in the box below.
Answer: MR(143)
=
$ per unit
-

Math
DifferentiationThe management of the producers of a famous hot sauce estimate that their profit (in dollars) from the daily production and sale of x cases (each case consisting of 24 bottles) of the hot sauce is given by
P(x) = -0.0004x³ + 12x - 20
(a) How many cases of the daily production and sale should be to make the largest possible profit? Round your answer to the nearest integer, if necessary. You MUST justify that your result is an optimal value.
(b)What is the largest possible profit the producers can make in 1 day? Round your answer to the nearest whole dollar.
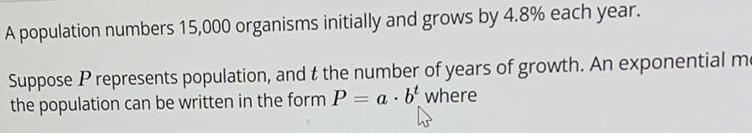
Math
DifferentiationA population numbers 15,000 organisms initially and grows by 4.8% each year. Suppose P represents population, and t the number of years of growth. An exponential me the population can be written in the form P = a.b^t where .

Math
DifferentiationThe demand for a certain portable USB battery charger is given by D(p) = -4p² +3p+5, where p represents the price in dollars.
(a) Find the rate of change of demand with respect to price.
(b) Find and interpret the rate of change of demand when the price is $12.
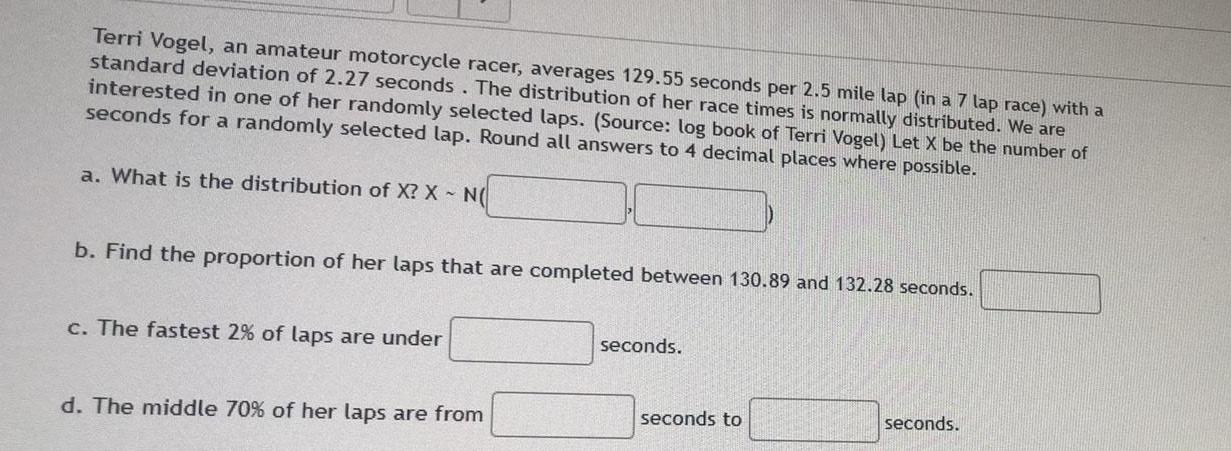
Math
DifferentiationTerri Vogel, an amateur motorcycle racer, averages 129.55 seconds per 2.5 mile lap (in a 7 lap race) with a standard deviation of 2.27 seconds. The distribution of her race times is normally distributed. We are interested in one of her randomly selected laps. (Source: log book of Terri Vogel) Let X be the number of seconds for a randomly selected lap. Round all answers to 4 decimal places where possible.
a. What is the distribution of X? X - N(
b. Find the proportion of her laps that are completed between 130.89 and 132.28 seconds.
c. The fastest 2% of laps are under
d. The middle 70% of her laps are from
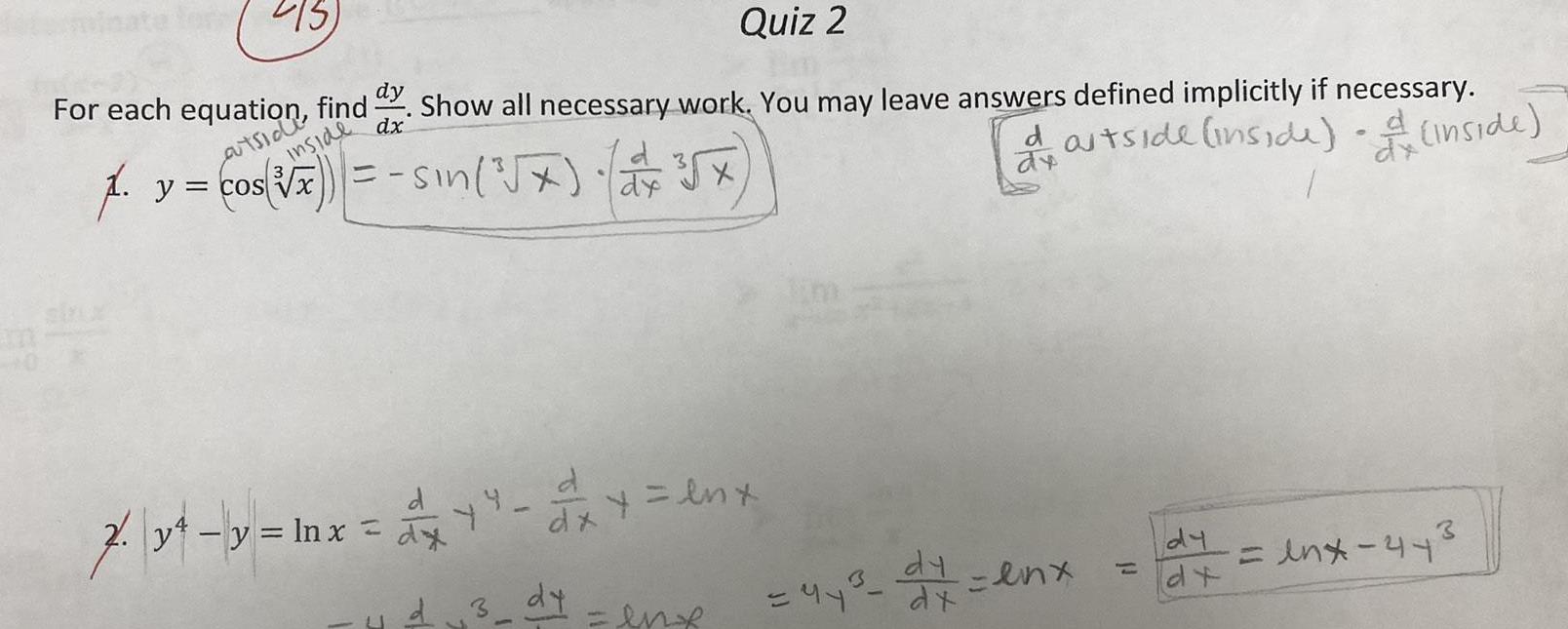
Math
Differentiation413)
For each equation, find-
dy. Show all necessary work. You may leave answers defined implicitly if necessary.
Quiz 2
dx
1. y = cos(√x)) = sin(³√7)
= (+²57)
autside
inside
dartside (inside) (inside).
7. y¹ - y = lnx = ax
d
+² - 2x + = lnx
d 3 dy
=enx
ax
dy
= 47³-17 = enx
dx
Ave
dy
df
3
=lnx-44²

Math
DifferentiationLet f(x) and g(x) be functions such that f'(-5) = g'(-5) and the line tangent to the graph of f at x = -5 is y = 4x + 2.
For each part, compute the desired value, if possible. Your answer must be an exact number. If it is not possible to determine the value from the given
(A) f(-5)=
(B) f'(-5) =
(C) g(-5)=
(D) g'(-5)=

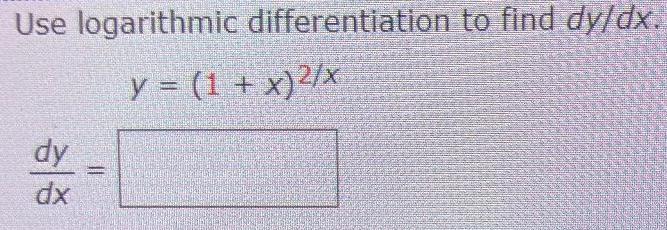
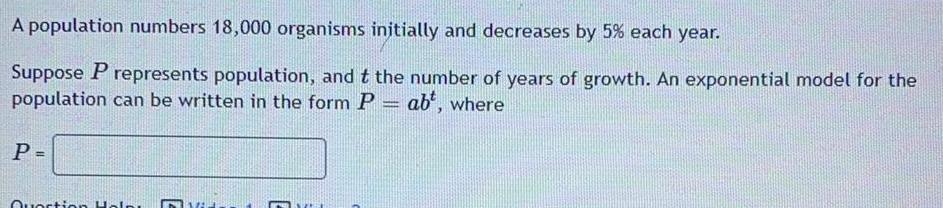
Math
DifferentiationA population numbers 18,000 organisms initially and decreases by 5% each year. Suppose P represents population, and t the number of years of growth. An exponential model for the population can be written in the form P = abt, where

Math
DifferentiationThere is 0.998615 probability that a randomly selected 20-year-old male lives through the year. A Fidelity life insurance company charges $178 for insuring that the male will live through the year. If the male does not survive the year, the policy pays our $110,000 as a death benefit. If a 20-year-old male purchases the policy, what is his expected value?
$32.65
-$29.61
- $26.10
-$25.65

Math
DifferentiationA ball is thrown upward and outward from a height of 7 feet. The height of the ball, f(x), in feet, can be modeled by
f(x) = -0.2x² +2.1x+7
where x is the ball's horizontal distance, in feet, from where it was thrown. Use this model to solve parts (a) through (c).
a. What is the maximum height of the ball and how far from where it was thrown does this occur?
The maximum height is feet, which occurs feet from the point of release.
(Round to the nearest tenth as needed.)

Math
DifferentiationJason jumped off a cliff into the ocean in Acapulco while vacationing with some friends. His height as a function of time could be modeled by the function h(t)=-16t2 +16t+480, where t is the time in seconds and h is the height in feet.
a. How long did it take for Jason to reach his maximum height?
b. What was the highest point that Jason reached?
c. Jason hit the water after how many seconds?

Math
Differentiation(1 point) Use the graph of y = |x² - 5| to determine
where the function is not differentiable.
The function is not differentiable at x =
(If there is more than one x-value, enter a comma-
separated list. If there are no x-values, enter "none".)

Math
Differentiation3.) For each of the following functions, find of and
(i) (2 pts) f(x, y) = x³ +y³ - 3x²y²
xy
x² + y²
(iii) (2 pts) f(x, y) = x²e³y
(ii) (2 pts) f(x, y) =
=
Simplify the final answer completely.
(iv) (2 pts) f(x, y) = arctan
(²).
Simplify the final answer com-
pletely. No complex fractions and no negative powers in the final an-
swer.
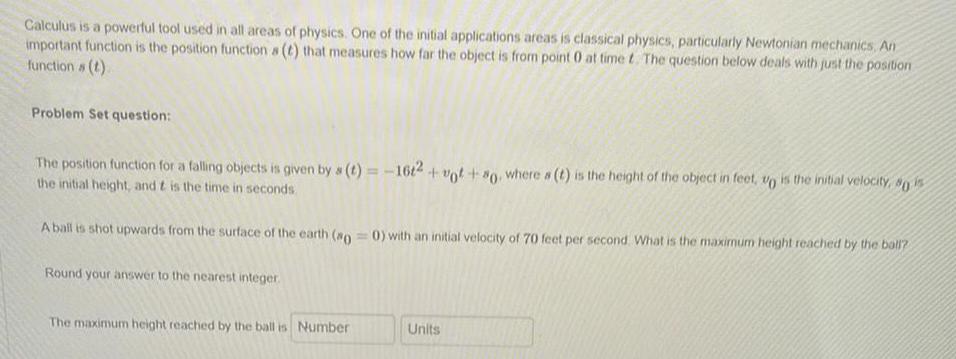
Math
DifferentiationCalculus is a powerful tool used in all areas of physics. One of the initial applications areas is classical physics, particularly Newtonian mechanics, An important function is the position function s (t) that measures how far the object is from point 0 at time t. The question below deals with just the position function s (t)
Problem Set question:
The position function for a falling objects is given by s (t)=-16t2 + v0t + s0, where a (t) is the height of the object in feet, v0 is the initial velocity, s0 is the initial height, and t is the time in seconds
A ball is shot upwards from the surface of the earth (s0 = 0) with an initial velocity of 70 feet per second What is the maximum height reached by the ball?
Round your answer to the nearest integer.
The maximum height reached by the ball is

Math
DifferentiationA plane flying horizontally at an altitude of 2 miles and a speed of 420 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 4 miles away from the station. (Round your answer to the nearest whole number.)