Functions Questions and Answers

Math
FunctionsThe half-life of radium-226 is 1,590 years.
(a) A sample of radium-226 has a mass of 50 mg. Find a formula for the mass of the sample that remains after t years.
(b) Find the mass after 1,500 years correct to the nearest milligram.
(c) When will the mass be reduced to 30 mg?

Math
FunctionsIf the function y = e-5 is vertically compressed by a factor of 6, reflected across the y-axis, and then shifted up 1 units,
what is the resulting function? Write your answer in the form y = ceª + b.
Provide your answer below:
y=0
Math
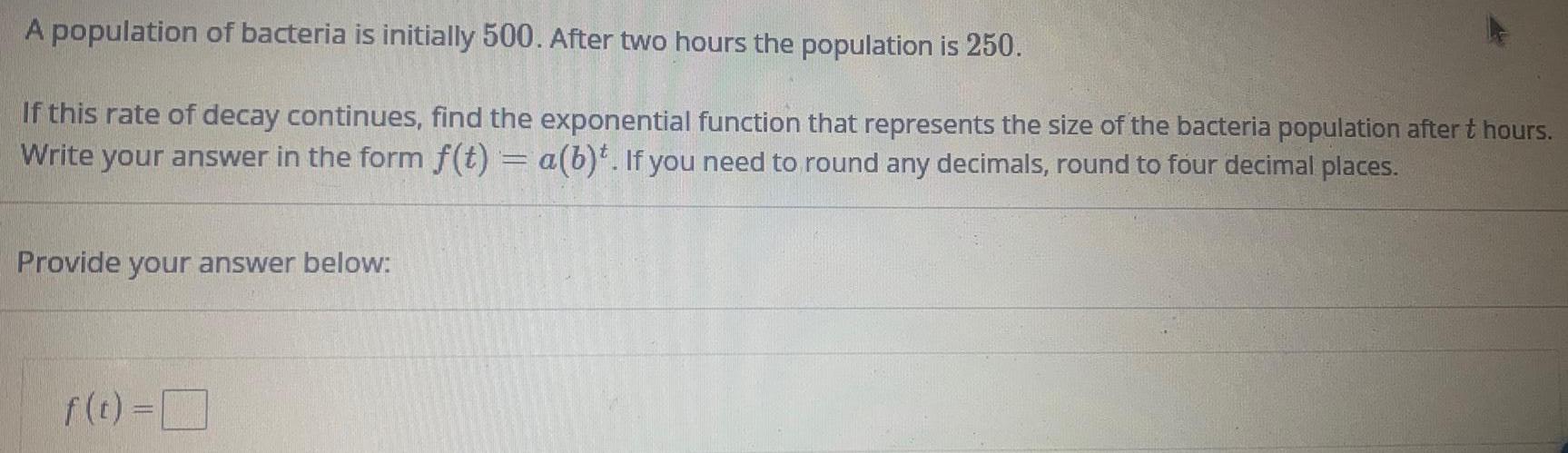
FunctionsA population of bacteria is initially 500. After two hours the population is 250.
If this rate of decay continues, find the exponential function that represents the size of the bacteria population after t hours.
Write your answer in the form f(t) = a(b)t. If you need to round any decimals, round to four decimal places.
Provide your answer below:
f(t) =

Math
Functions(1 point) Use the graph of y = (6 - x) / (6 + x) to determine where the function is not differentiable.
The function is not differentiable at x =
(If there is more than one x-value, enter a comma-separated list. If there are no x-values, enter "none".)

Math
FunctionsTurner is baking apple tartlets for a special celebration. He has already made 6 tartlets, and
he can make 3 more tartlets with each additional egg he has in the fridge.
Write an equation that shows how the total number of tartlets, y, depends on the number of
eggs in the fridge, x.
y =

Math
FunctionsSuppose that the relation H is defined as follows.
H={(m, 0), (1, 1), (7, m), (5, n)} ¹
Give the domain and range of H.
Write your answers using set notation.

Math
FunctionsThe function that converts pounds of Country A to dollars of Country B is f(x) = 1.9738x, where x is the number of pounds of Country A and f(x) is the number of dollars
of Country B. Complete parts a and b below.
a. Find the inverse function for f.
f¯1(x)=
(Simplify your answer. Use integers or decimals for any numbers in the expression. Round to six decimal places as needed.)

Math
FunctionsFind all horizontal and vertical asymptotes (if any). (If an answer does not exist, enter DNE. Enter your answers as a comma-separated list of equations.)
5x² + 7x
A-1
vertical asymptote(s) ||
r(x) =
horizontal asymptote
X
X

Math
FunctionsLet f(x) = 4√
If g(x) is the graph of f(x) shifted up 2 units and right 2 units, write a formula for g(x)
g(x)=
Enter √✓ as sqrt(x)
Math
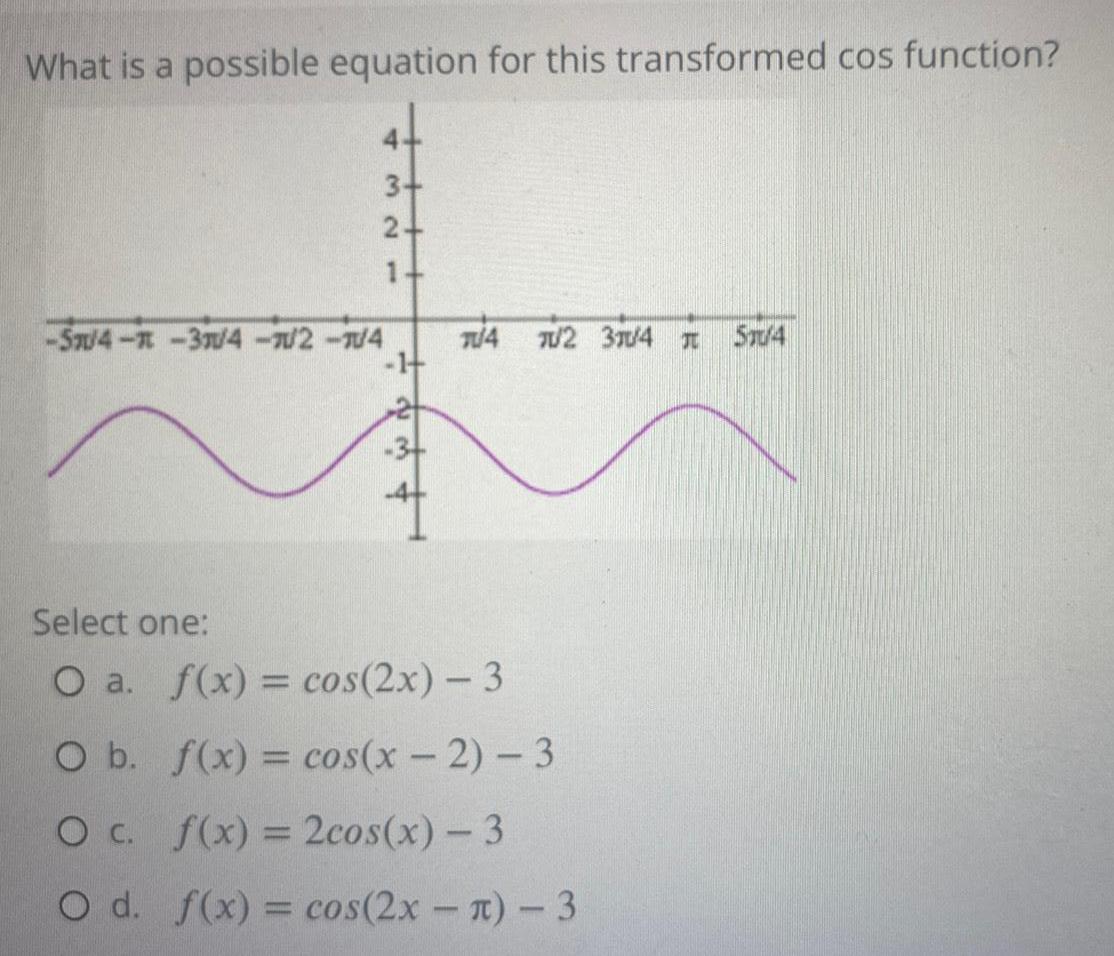
FunctionsWhat is a possible equation for this transformed cos function?
Select one:
a. f(x) = cos(2x) - 3
b. f(x) = cos(x-2)-3
c. f(x) = 2cos(x) - 3
d. f(x) = cos(2x - π) - 3
Math
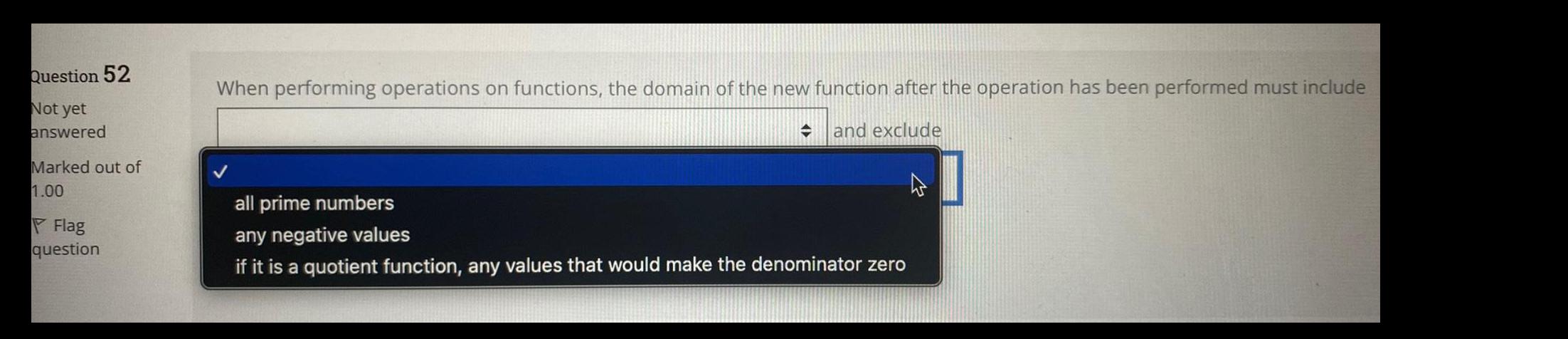
FunctionsWhen performing operations on functions, the domain of the new function after the operation has been performed must include and exclude
all prime numbers
any negative values
if it is a quotient function, any values that would make the denominator zero

Math
FunctionsGiven f(x) = 1/ x+1 and g(x) = x² — 4, if you were asked to find ()(x), what would be the restrictions on the domain of the quotient function?
Select one:
a. x≠-2, 2
b. No restrictions; Domain is all real numbers
c. x≠-2, -1, 2
d.x≠0
e.X ≠-1
Math
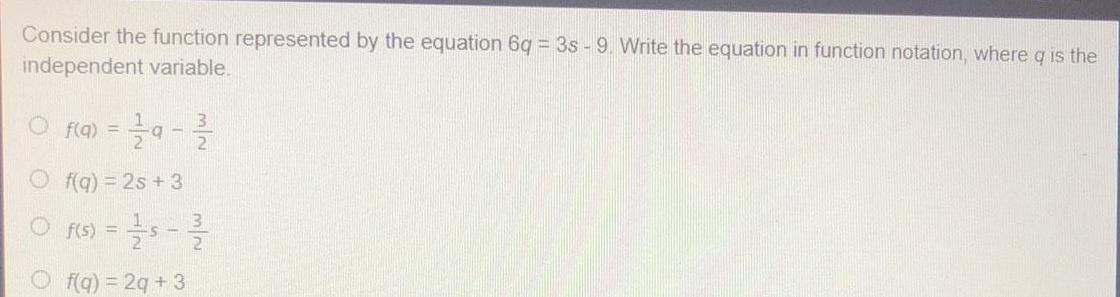
FunctionsConsider the function represented by the equation 6q = 3s - 9. Write the equation in function notation, where q is the independent variable.

Math
FunctionsUse implicit differentiation to find an equation of the tangent line to the curve at the given point.
y sin (12x) = x cos(2y),
(π/2, π/4)

Math
FunctionsWhich of the following illustrates how the graphs of y = bx and y = (1/b)x with b > 1 are related?
A. One is a reflection over the x-axis of the other.
B. One is a reflection over the y-axis of the other
C. Both A and B above
D. None of the above

Math
FunctionsA country's population in 1990 was 123 million. In 2002 it was 128 million. Estimate the population in 2013 using the exponential growth formula. Round your answer to the nearest million. P = Aekt
Math
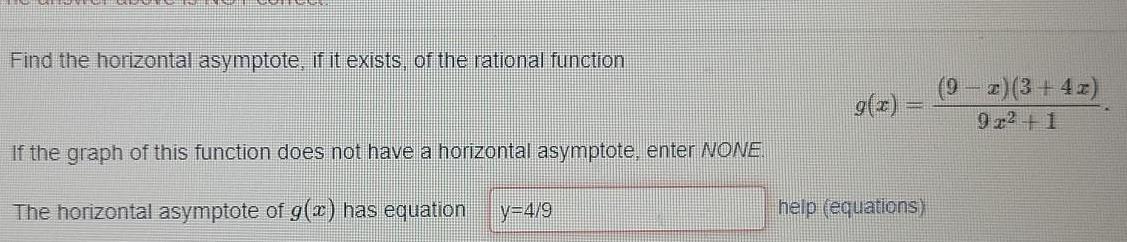
FunctionsFind the horizontal asymptote, if it exists, of the rational function
g(x)= (9-x)(3+4x) / (9x^2 +1)

Math
FunctionsLet g be a function. Which statements are true for all functions g?
Select all that apply.
For an element x in the range, g(x) represents an element in the domain.
The function g assigns each element of the domain exactly two element of the range.
The value of g(a) is the output of g corresponding to the input a.
The function g assigns each element of the domain exactly one element of the range.

Math
FunctionsThe points at which a graph changes direction (from increasing to decreasing or decreasing to increasing) are called
end points.
turning points.
minimum points.
maximum points.
changing points.
Math
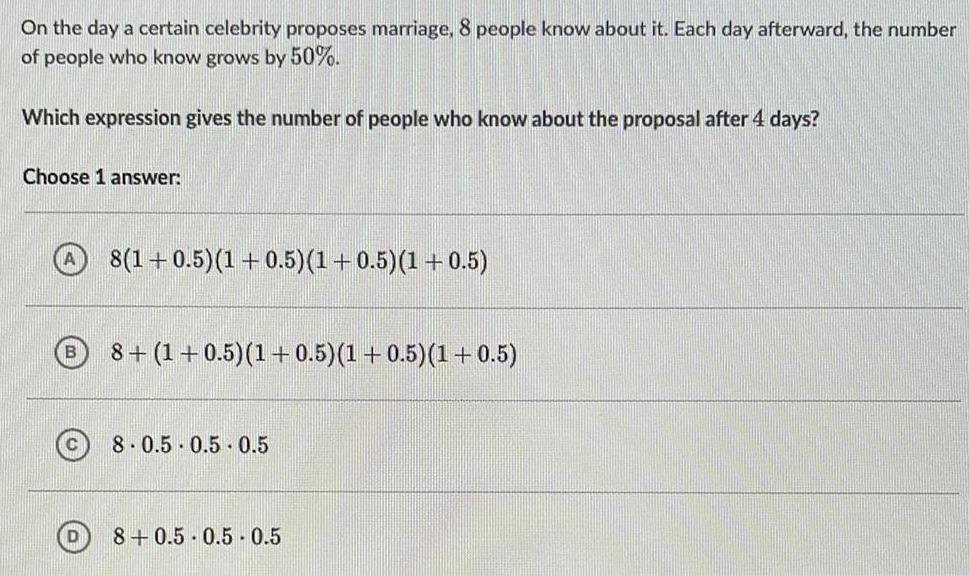
FunctionsOn the day a certain celebrity proposes marriage, 8 people know about it. Each day afterward, the number of people who know grows by 50%.
Which expression gives the number of people who know about the proposal after 4 days?
Choose 1 answer:
8(1+0.5)(1+0.5)(1+0.5)(1+0.5)
8+ (1+0.5)(1+0.5)(1+0.5)(1+0.5)
8 0.5 0.5 0.5
8+0.5 0.5-0.5
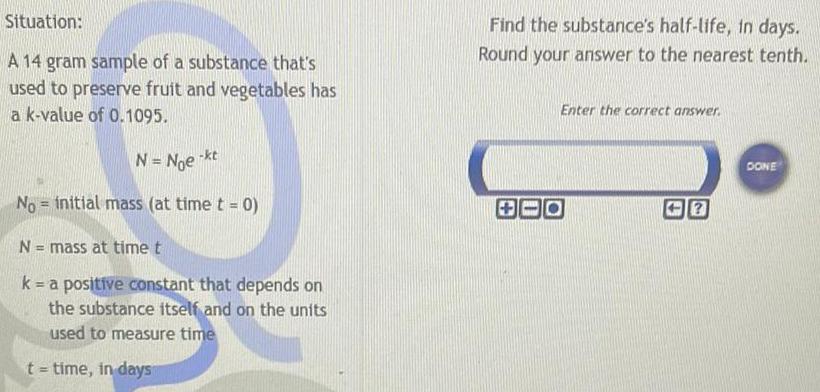
Math
FunctionsA 14 gram sample of a substance that's used to preserve fruit and vegetables has a k-value of 0.1095.
N = Noe^-kt
N0= initial mass (at time t = 0)
N = mass at time t
k = a positive constant that depends on the substance itself and on the units used to measure time
t = time, in days
Find the substance's half-life, in days.

Math
FunctionsLexington High School has an annual growth rate of 4.7%. Three years ago there were 1500 students at the school.
a. How many students are there now?
b. How many students were there 5 years ago?
c. How many students will there be n years from now?
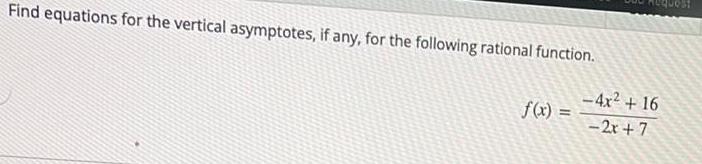
Math
FunctionsFind equations for the vertical asymptotes, if any, for the following rational function.
f(x) =-4x² + 16/-2x+7
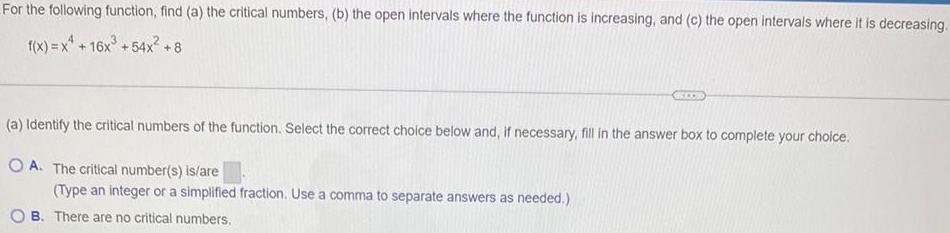
Math
FunctionsFor the following function, find (a) the critical numbers, (b) the open intervals where the function is increasing, and (c) the open intervals where it is decreasing.
f(x) = x^4 + 16x³ +54x² +8
(a) Identify the critical numbers of the function. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The critical number(s) is/are
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)
B. There are no critical numbers.
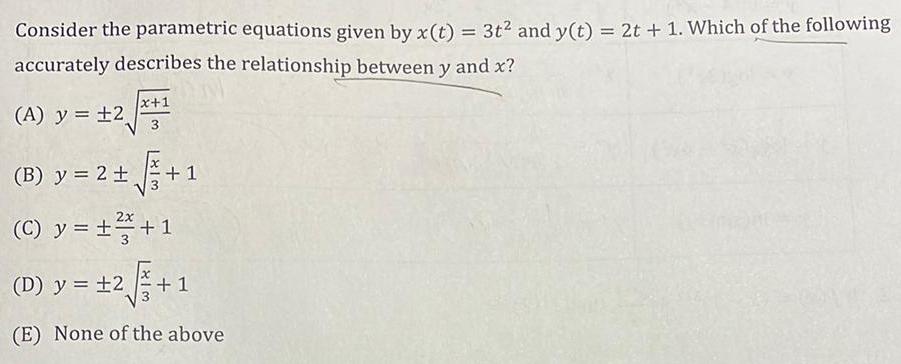
Math
FunctionsConsider the parametric equations given by x(t) = 3t² and y(t) = 2t + 1. Which of the following
accurately describes the relationship between y and x?
(A) y = ±2√x+1/3
(B) y = 2 ± √x3+1
(C) y = ±2x/3+1
(D) y = ±√x/3+1
(E) None of the above

Math
Functions1. A rocket is tossed from a platform and follows a parabolic path through the air. The height of the
rocket in meters is given by h(t) = -3t2 + 10t+8, where t is measured in seconds.
a) How high is the rocket off the ground when it is thrown?
b) For what times is the height of the rocket above 10m? Round to 2 dec. places.
(1 mark)
(3 marks)

Math
FunctionsFind the following for the function f(x) = 4x² + 2x - 4.
(a) f(0)
(b) f(4)
(c) f(-4)
(d) f(-x)
(e) - f(x)
(f) f(x + 3)
(g) f(3x)
(h) f(x + h)

Math
FunctionsIf
f(x,y) =5x - 2y/√x² + y²-7
then the domain of is D= {(x,y)| x² + y² >7}
Select one:
True
False
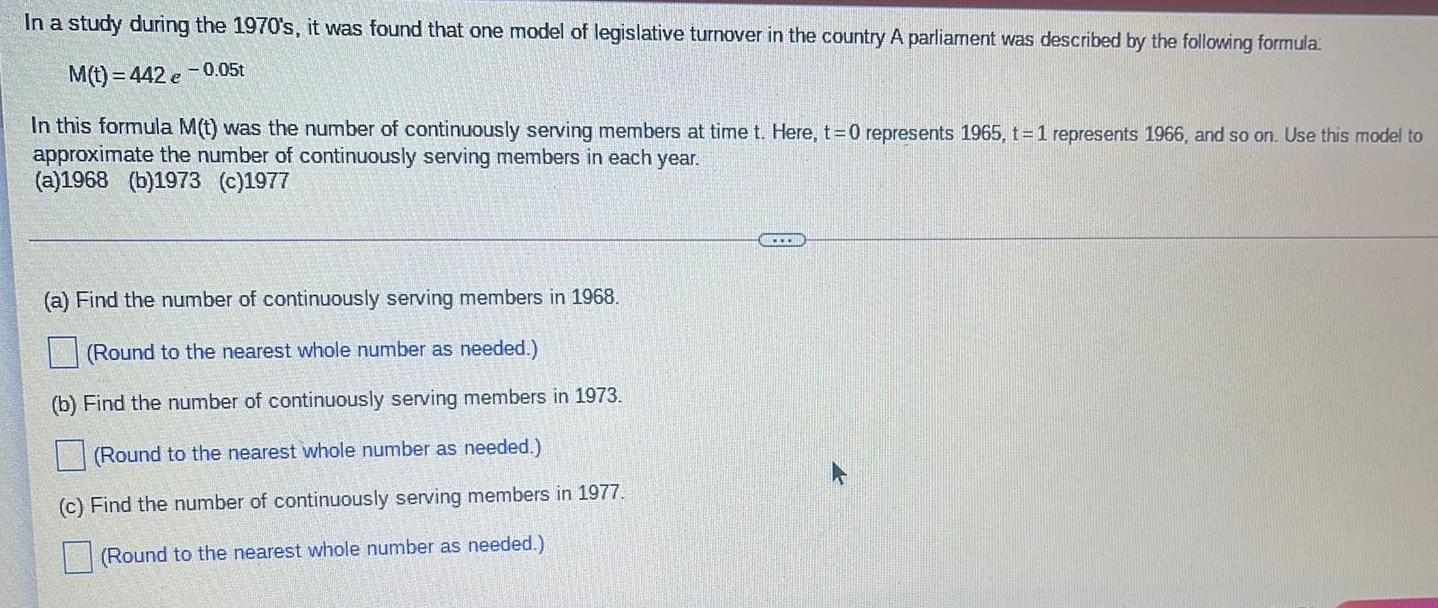
Math
FunctionsIn a study during the 1970's, it was found that one model of legislative turnover in the country A parliament was described by the following formula
M(t)=442e-0.05t
In this formula M(t) was the number of continuously serving members at time t. Here, t=0 represents 1965, t= 1 represents 1966, and so on. Use this model to
approximate the number of continuously serving members in each year.
(a)1968 (b)1973 (c)1977
(a) Find the number of continuously serving members in 1968.
(Round to the nearest whole number as needed.)
(b) Find the number of continuously serving members in 1973.
(Round to the nearest whole number as needed.)
(c) Find the number of continuously serving members in 1977.
(Round to the nearest whole number as needed.)
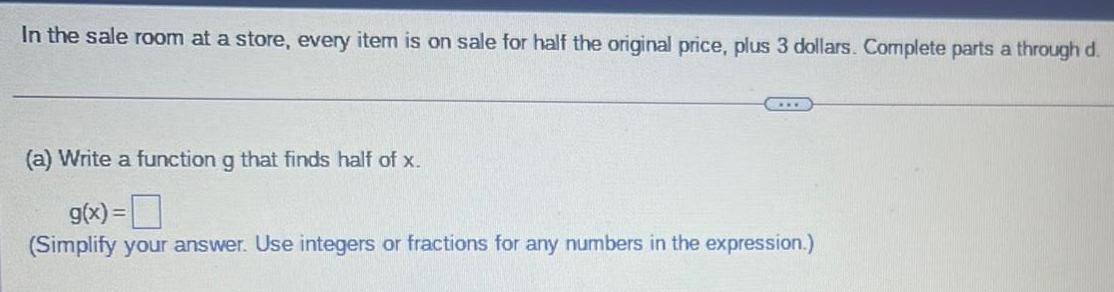
Math
FunctionsIn the sale room at a store, every item is on sale for half the original price, plus 3 dollars. Complete parts a through d.
(a) Write a function g that finds half of x.
g(x) =
(Simplify your answer. Use integers or fractions for any numbers in the expression.)

Math
FunctionsIn a mountain range of California, the percent of moisture that falls as snow rather than rain can be approximated by the function p(h) = 75 In (h) - 587, where h is the
altitude in feet and p(h) is the percent of an annual snow fall at the altitude h. Use the function to approximate the amount of snow at the altitudes 5000 feet and 9000
feet.
...
The percent of annual precipitation that falls as snow at 5000 feet is approximately.
(Round to the nearest integer.)

Math
Functions(Lesson 32) The population of a town is decreasing at a rate of 1% per year. In 2000 there were 1300 people. Write an
exponential decay function to model this situation. Then find the population in 2008.
A Approximately 1200 people
B Approximately 1100 people
C Approximately 1500 people
D Approximately 1300 people

Math
FunctionsExpress the quadratic function in factored form. Then determine the zeros, the equation of the axis of
symmetry, the maximum/minimum value, the direction of opening and the coordinates of the vertex.
f(x) = x² - 2x + 24
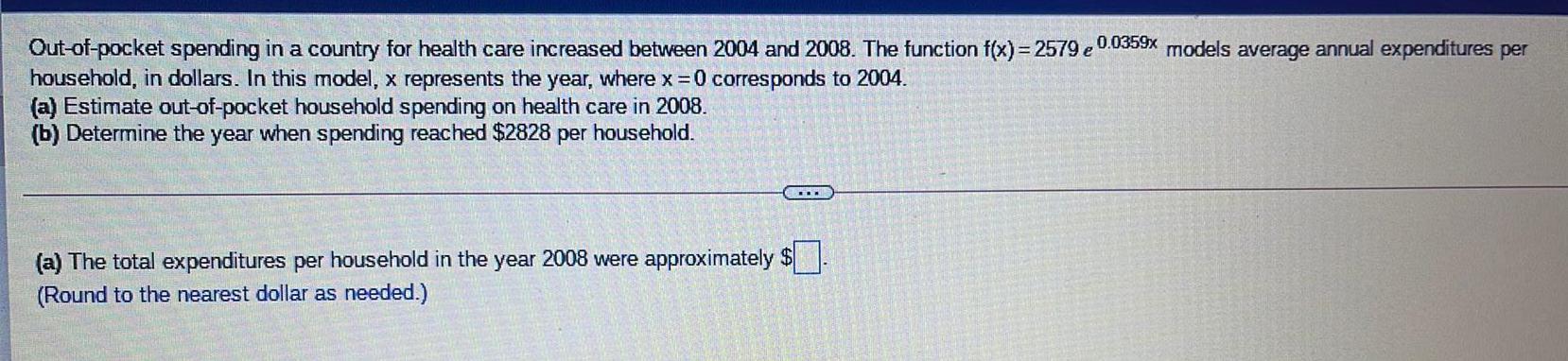
Math
FunctionsOut-of-pocket spending in a country for health care increased between 2004 and 2008. The function f(x)=2579 e 0.0359x models average annual expenditures per household, in dollars. In this model, x represents the year, where x = 0 corresponds to 2004.
(a) Estimate out-of-pocket household spending on health care in 2008.
(b) Determine the year when spending reached $2828 per household.

Math
FunctionsWhat effect does the graph y = f(x) + k have on its parent function when k < 0?
The graph is shifted upwards.
The graph is shifted leftwards.
The graph is shifted downwards.
The graph is shifted rightwards.

Math
FunctionsUse a table of function values to approximate an x-value in which the exponential function exceeds the polynomial function.
f(x)=3(4)^(2x-4)
h(x) = (x+2)^3+1
x = 4
x = 2
x = -3
x = 0
![A model of carry-on luggage has a length that is 5 inches greater than its depth. Airline regulations require that the sum of the length, width, and depth cannot exceed 57 inches. These conditions, with the assumption that this sum is 57 inches, can be modeled by the function V(x) that gives the luggage's volume, in cubic inches, in terms of its depth, x, in inches. If its volume is 1500 cubic inches, determine two possibilities for its depth. Volume = depth * length* width: 57-(depth + length)
V(x)= x * (x+5). [57-(x+x+5)]
V(x)= x(x + 5)(52-2x)](https://media.kunduz.com/media/sug-question/raw/70200853-1657468380.2735493.jpeg?w=256)
Math
FunctionsA model of carry-on luggage has a length that is 5 inches greater than its depth. Airline regulations require that the sum of the length, width, and depth cannot exceed 57 inches. These conditions, with the assumption that this sum is 57 inches, can be modeled by the function V(x) that gives the luggage's volume, in cubic inches, in terms of its depth, x, in inches. If its volume is 1500 cubic inches, determine two possibilities for its depth. Volume = depth * length* width: 57-(depth + length)
V(x)= x * (x+5). [57-(x+x+5)]
V(x)= x(x + 5)(52-2x)
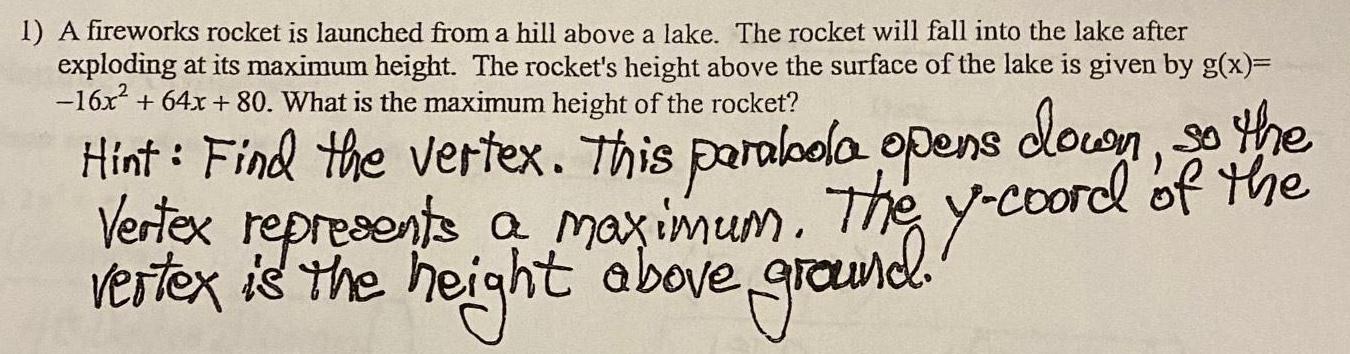
Math
Functions1) A fireworks rocket is launched from a hill above a lake. The rocket will fall into the lake after
exploding at its maximum height. The rocket's height above the surface of the lake is given by g(x)=
-16x² + 64x+80. What is the maximum height of the rocket?
Hint: Find the vertex. This parabola opens down, so the
vertex is the height
Vertex represents a maximum. The y-coord of the
above ground.

Math
FunctionsA fraternity charged $2.00 admission for dudes and $1.00 admission for ladies to their finals week bash. The fraternity made $65.00 and sold 45 tickets. How many ladies attended the party?

Math
Functions10. The function f(t) = 1200(1.75)60t represents the change in a quantity over t minutes. What
does the constant 1.75 reveal about the rate of change of the quantity?
The function is
exponentially are a rate of
% every

Math
FunctionsWhich statement is true about a function f(x), where f'(x)=3x²-²? (6 points)
f is increasing for x > 0.874 because f '(x) > 0 for x > 0.874
f is decreasing for x > 0.874 because f '(x) > 0 for x > 0.874
f is increasing for x < 0 because f '(x) < 0 for x < 0
fis decreasing for x < 0 because f '(x) < 0 for x < 0
X


Math
FunctionsThe population of a town increased from 3500 in 2010 to 4100 in 2017. Let x = 0 for year 2010.
a) Build a model exponential function of the form of this town. Clearly show your algebraic work. P(t) = P0e^kt Pe for the population
b)Use your answer from part (a) to predict the year when the town's population will reach 7000. Clearly show your algebraic work.

Math
FunctionsJasmine invests $5,400 in an account with a fixed annual interest rate of 8% compounded quarterly. What will be the account balance after 5 years? Write and solve an equation, where B represents the account balance, and t represents time in years.
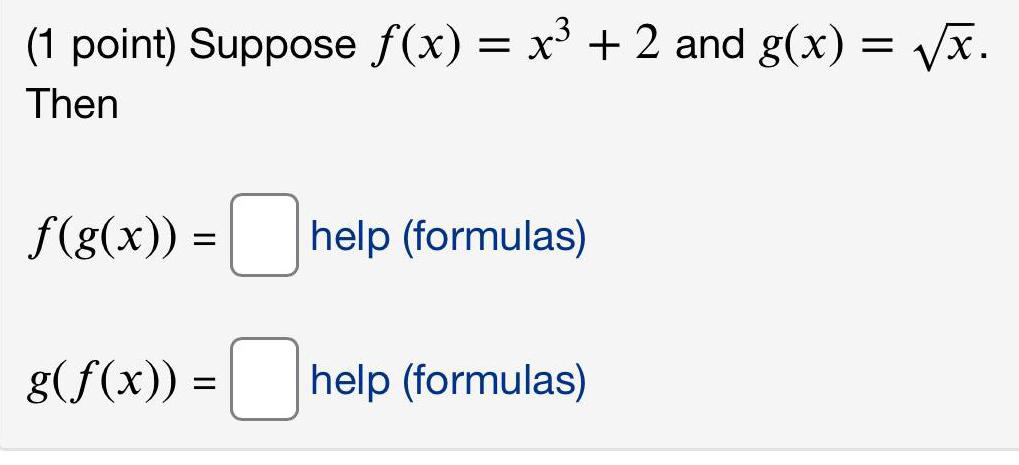

Math
FunctionsFind the gradient of the function at the given point.
f(x, y, z)=√x² + y² + z² , (5, 2, 9)
Find the maximum value of the directional derivative at the given point.

Math
FunctionsComplete the square of the given quadratic expression. Then, graph the function using the technique of shifting.
f(x)=x² +8x+15