Functions Questions and Answers

Math
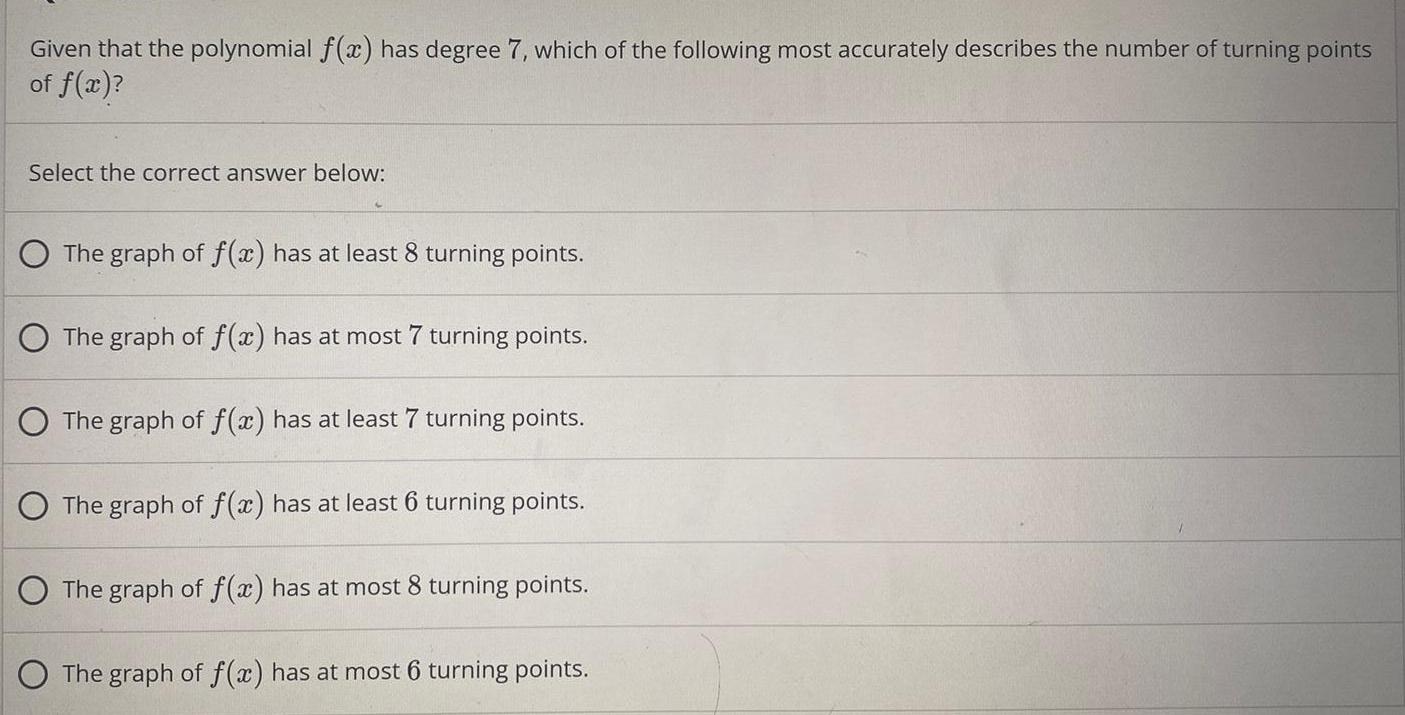
FunctionsGiven that the polynomial f(x) has degree 7, which of the following most accurately describes the number of turning points of f(x)?
Select the correct answer below:
The graph of f(x) has at least 8 turning points.
The graph of f(x) has at most 7 turning points.
The graph of f(x) has at least 7 turning points.
The graph of f(x) has at least 6 turning points.
The graph of f(x) has at most 8 turning points.
The graph of f(x) has at most 6 turning points.
Math
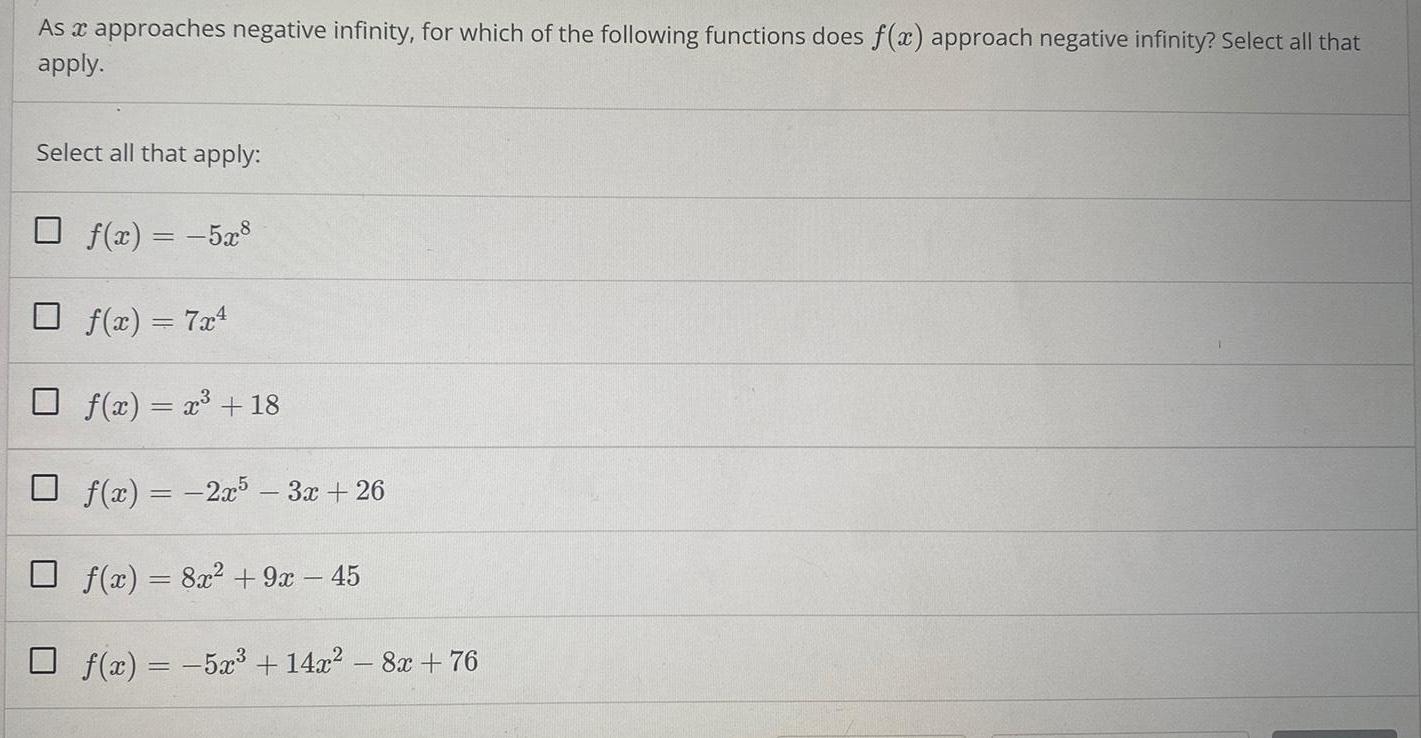
FunctionsAs a approaches negative infinity, for which of the following functions does f(x) approach negative infinity? Select all that apply.
Select all that apply:
f(x) = -5x8
f(x) = 7x²
f(x) = x³ + 18
f(x) = 2x5 - 3x +26
f(x) = 8x² + 9x - 45
ƒ(x) = −5x³ + 14x²-8x + 76

Math
Functionsg(x) = 4x
f(x)=-3x+3
Find (g. f)(x)
A) 2x² - 11x + 12
B) -12x² + 12x
C) -12x² - 12x
D)-x+x+4x-4
Math
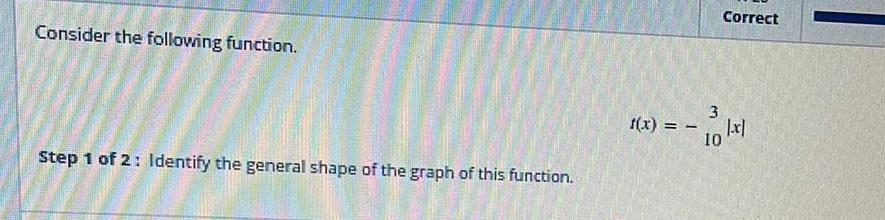
FunctionsConsider the following function.
f(x) = -3/10 |x|
Identify the general shape of the graph of this function.

Math
FunctionsFind the real zeros of f. Use the real zeros to factor f.
f(x)= x³ +6x²-9x-14
The real zero(s) of f is/are
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers.
Use the real zero(s) to factor f.
f(x) =
(Factor completely. Type an exact answer, using radicals as needed. Use integers or fractions for any numbers in the expression)

Math
FunctionsWrite a quadratic equation having the given number as a solution.
9, only solution (Hint: It must be a repeated solution.)

Math
FunctionsSuppose that the number of employees in a new company is expected to grow, with the number of
employees modeled by N = 1000(0.02)0.7¹, where t is the number of years after the company was
formed.
a) How many employees did the company have when it started?
N= employees
(Do not round until the final answer. Then round to the nearest integer as needed.)

Math
FunctionsThe president of a company predicts that sales will increase rapidly after a new product is brought to the market and that the number of units sold monthly can be modeled by N = 50,000(0.4)0.2¹, where t represents the number of months after the product
is introduced.
a) How many units will be sold by the end of the fourth month?
N = units
(Do not round until the final answer. Then round to the nearest integer as needed.)

Math
FunctionsGraph f(x) = 4x-3 + 2 using transformations by first graphing the basic exponential
function (parent function), then the progression of transformations (in the correct order).
State the domain, range, and horizontal asymptote.

Math
FunctionsChoose the term from the box that best completes each statement.
end behavior
symmetric about a line
even function
power function
1. A function is
2. The.
and as x approaches negative infinity.
3. A(n)
4. A function is.
if the line divides the graph into two identical parts.
of a graph of a function is the behavior of the graph as x approaches infinity
5. A(n).
6. A(n)
symmetric about a point
odd function
has a graph symmetric about the origin, thus f(x) = -f(-x).
central point but in the opposite direction.
if each point on the graph has a point the same distance from the
has a graph symmetric about the y-axis, thus f(x) = f(-x).
is a function of the form P(x) = ax", where n is a non-negative integer.
Math
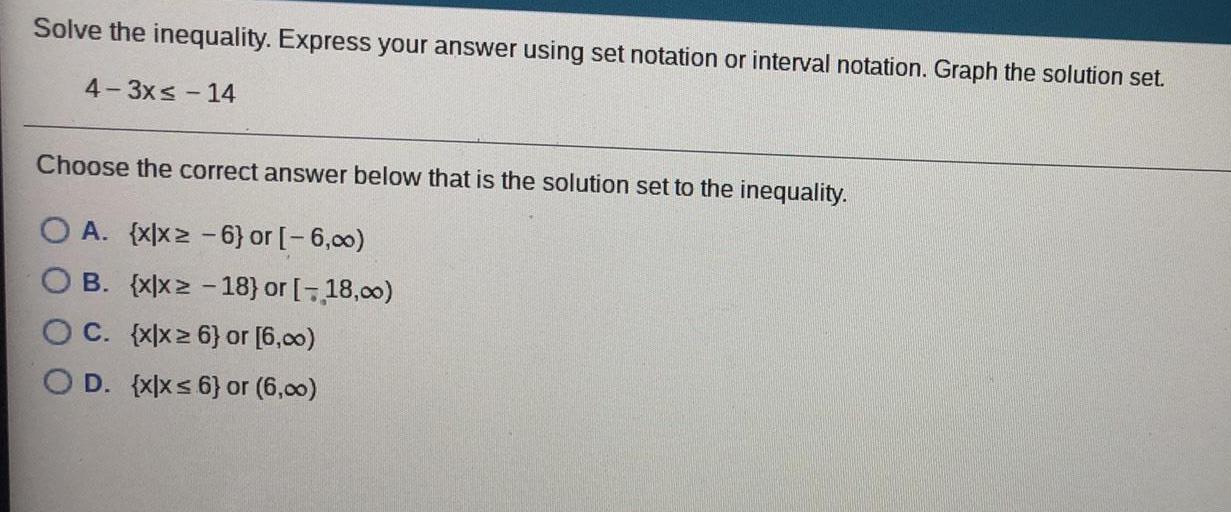
FunctionsSolve the inequality. Express your answer using set notation or interval notation. Graph the solution set.
4-3x≤ - 14
Choose the correct answer below that is the solution set to the inequality.
OA. {x|x2 -6} or [-6,00)
B. {xx≥ -18) or [-18,00)
OC. (xlx ≥ 6) or [6,00)
OD. (xx≤6) or (6,00)
Math
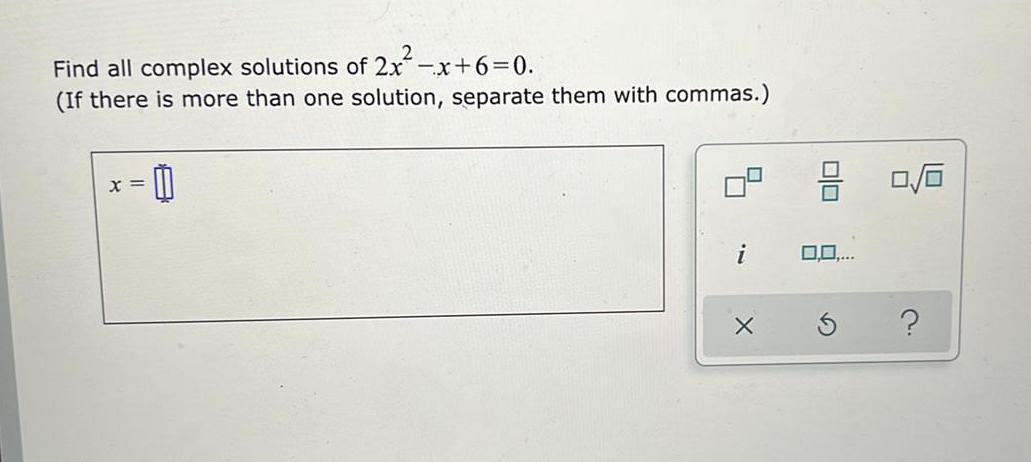
FunctionsFind all complex solutions of 2x²-x+6=0.
(If there is more than one solution, separate them with commas.)
x =
X
0.0..
0/6
?

Math
FunctionsConsider the function f(x) = x² + 3x - 3:
(a) Evaluate f(2)
(b) Evaluate f(-2)
(c) Find all x such that f(x) = 7
(d) Find all x such that f(x) = 9
(For part (d) express the answers exactly and round to four places.)
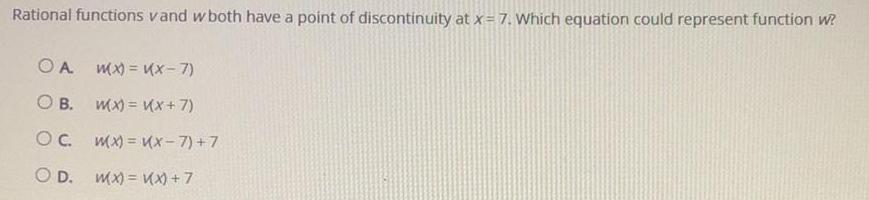
Math
FunctionsRational functions vand w both have a point of discontinuity at x = 7. Which equation could represent function w?
A MX)= V(X-7)
B. M(x) = V(x+7)
C. M(x)=V(x-7)+7
D. M(x) = V(X) + 7
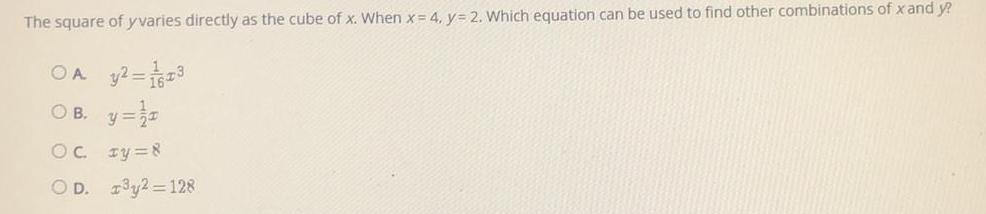
Math
FunctionsThe square of y varies directly as the cube of x. When x = 4, y = 2. Which equation can be used to find other combinations of x and y?

Math
FunctionsSelect the correct answer.
The domain of rational function g is the same as the domain of rational function f. Both fand g have a single x-intercept at x = -10. Which equation could represent function g?
A (x)=10x)
B. g(x)=x+10)
C. g(x)=f(x) + 10
D. g(x)=f(x) - 10
Math
FunctionsSelect the correct answer.
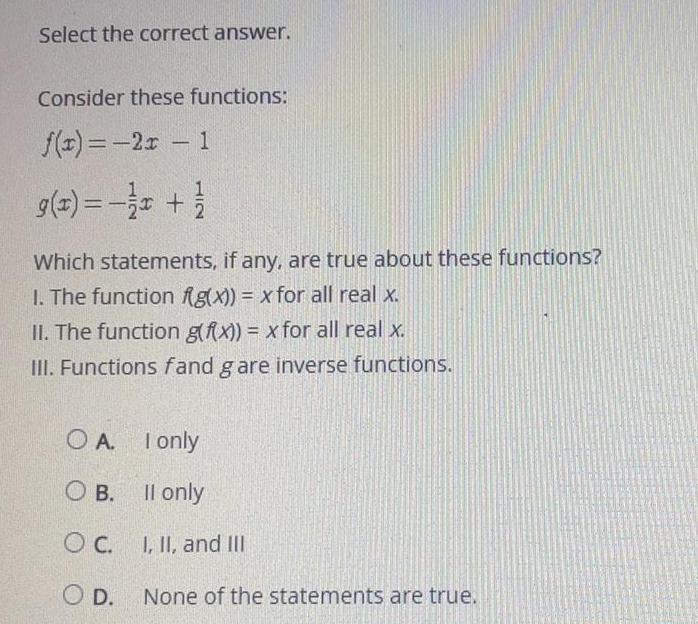
Consider these functions:
f(x) = -2x - 1
g(x) = -1/2 x + 1/2
Which statements, if any, are true about these functions?
1. The function f(g(x)) = x for all real x.
II. The function g(x)) = x for all real x.
III. Functions fand g are inverse functions.
A. I only
B. II only
C. I, II, and III
D. None of the statements are true.

Math
FunctionsA solid object is dropped into a pond with a
temperature of 20 degrees Celsius. The function
f(t) = Ce-kt) + 20 represents the situation,
where t is time in minutes, C is a constant, and
k = 0.0399.
After 4 minutes the object has a temperature of
35 degrees Celsius. What was the initial
temperature of the object? Round your answer to
the nearest tenth, and do not include units.
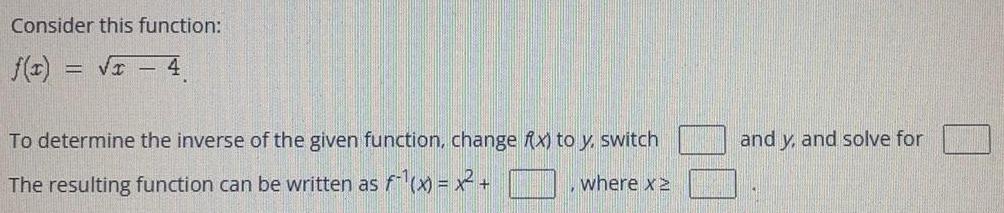
Math
FunctionsConsider this function:
f(x)=√x - 4
To determine the inverse of the given function, change fx) to y, switch and solve for
The resulting function can be written as f(x) = x² + where x≥
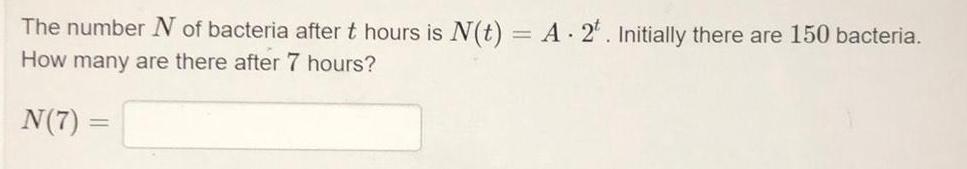
Math
FunctionsThe number N of bacteria after t hours is N(t) = A 2. Initially there are 150 bacteria.
How many are there after 7 hours?
N(7) =
=
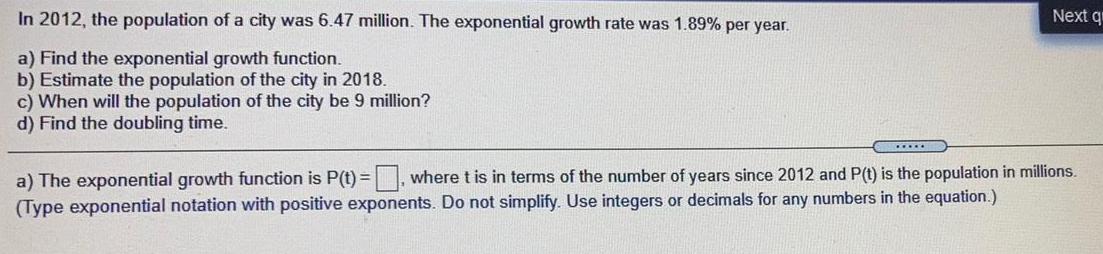
Math
FunctionsIn 2012, the population of a city was 6.47 million. The exponential growth rate was 1.89% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 9 million?
d) Find the doubling time.
*****
Next q
a) The exponential growth function is P(t)=, where t is in terms of the number of years since 2012 and P(t) is the population in millions.
(Type exponential notation with positive exponents. Do not simplify. Use integers or decimals for any numbers in the equation.)
![Recall that one method for treating this type of limit is by taking the natural logarithm. If we let y = [f(x)]⁹(x),
then In(y) = g(x) In (f(x)). Applying this method gives the following result.
y = (1 - 5x)1/x
In(y) = ¹/in(1-([
× )x)
We note that this leads to an indeterminate product on the right side, which is of type](https://media.kunduz.com/media/sug-question/raw/58237665-1657717971.103956.jpeg?w=256)
Math
FunctionsRecall that one method for treating this type of limit is by taking the natural logarithm. If we let y = [f(x)]⁹(x),
then In(y) = g(x) In (f(x)). Applying this method gives the following result.
y = (1 - 5x)1/x
In(y) = ¹/in(1-([
× )x)
We note that this leads to an indeterminate product on the right side, which is of type
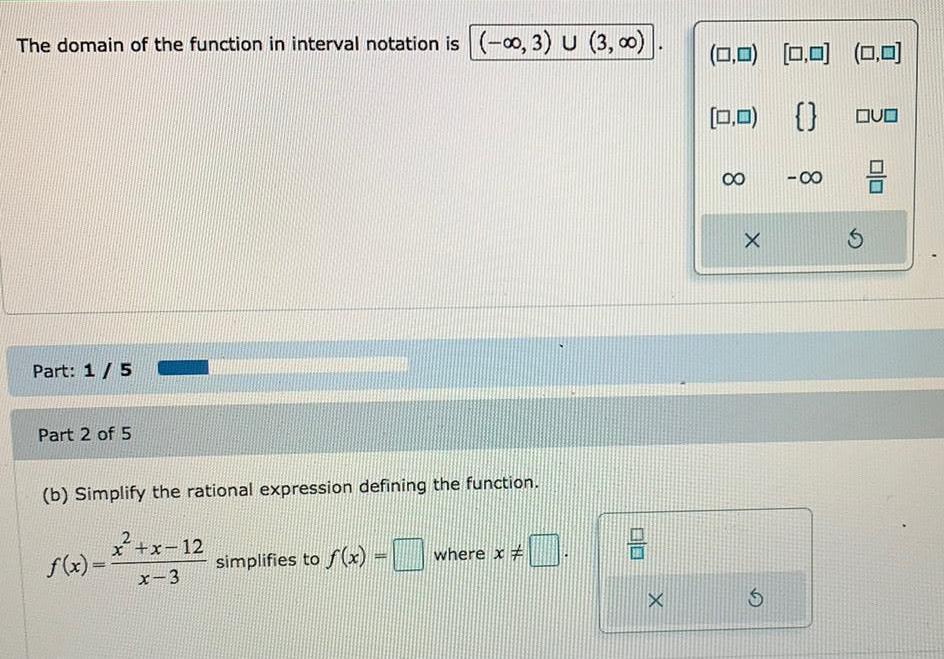
Math
FunctionsThe domain of the function in interval notation is (-∞, 3) U (3,∞)
(b) Simplify the rational expression defining the function.
f(x)=x^2+x-12/x-3
simplifies to f(x) = ___where x≠___
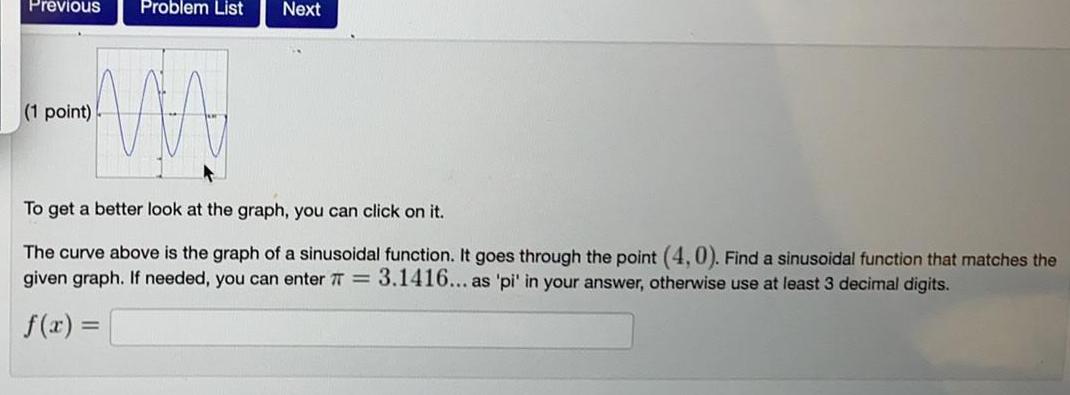
Math
Functionst)
Next
MA
To get a better look at the graph, you can click on it.
The curve above is the graph of a sinusoidal function. It goes through the point (4,0). Find a sinusoidal function that matches the
given graph. If needed, you can enter TT= 3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits.
f(x) =

Math
FunctionsThe exponential function
D(t) = 347(1.024)t
gives the number of bachelor's degrees, in thou-
sands, earned in the United States t years after 1970
(Sources: National Center for Educational Statistics;
U.S. Department of Education). Find the number of
bachelor's degrees earned in 1985, in 2000, and in
2014. Then estimate the number of bachelor's degrees
that will be earned in 2020. Round to the nearest
thousand degrees.
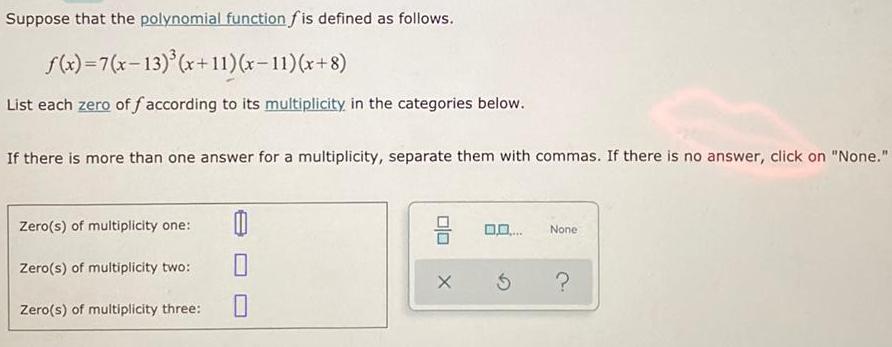
Math
FunctionsSuppose that the polynomial function fis defined as follows.
f(x)=7(x-13)³(x+11) (x-11) (x+8)
List each zero off according to its multiplicity in the categories below.
If there is more than one answer for a multiplicity, separate them with commas. If there is no answer, click on "None."
Zero(s) of multiplicity one:
Zero(s) of multiplicity two:
Zero(s) of multiplicity three:

Math
Functions. Salvage Value. A landscape company purchased a
backhoe for $56,395. The value of the backhoe each
year is 90% of the value of the preceding year. After
t years, its value, in dollars, is given by the exponen-
tial function
V(t) = 56,395 (0.9)'.
I
a) Graph the function.
b) Find the value of the backhoe after 0, 1, 3, 6, and
10 years. Round to the nearest dollar.
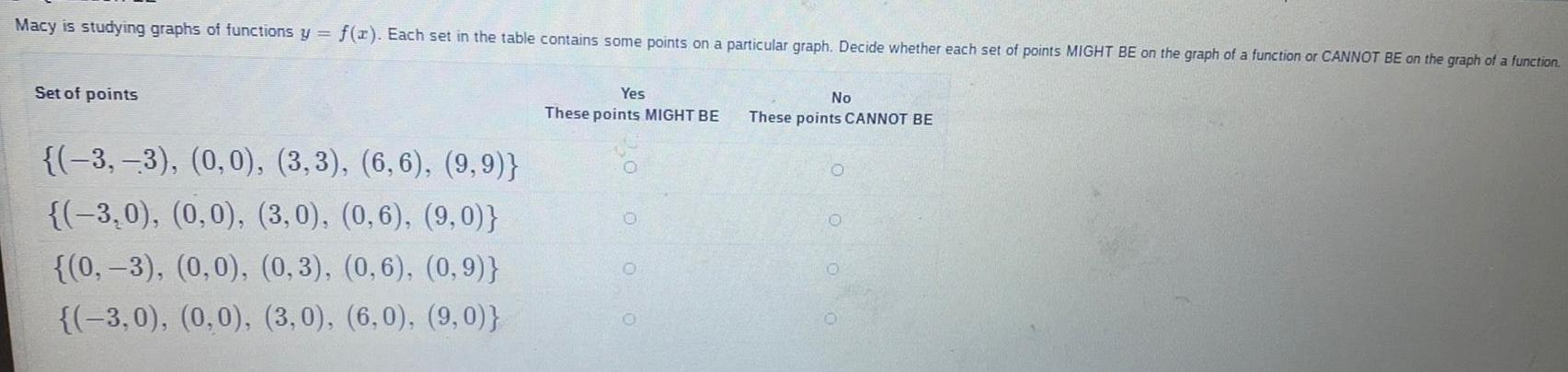
Math
FunctionsMacy is studying graphs of functions y = f(x). Each set in the table contains some points on a particular graph. Decide whether each set of points MIGHT BE on the graph of a function or CANNOT BE on the graph of a function.
Yes
These points MIGHT BE
Set of points
{(-3,-3), (0, 0), (3,3), (6,6), (9,9)}
{(–3,0), (0,0), (3,0), (0,6), (9,0)}
{(0, -3), (0,0), (0,3), (0,6), (0,9)}
{(-3,0), (0,0), (3,0), (6,0), (9,0)}
No
These points CANNOT BE
O

Math
FunctionsAn object moves in simple harmonic motion with period 8 minutes and amplitude 12 m. At time t=0 minutes, its displacement d from rest is - 12 m, and initially it moves in a positive direction.
Give the equation modeling the displacement d as a function of time t.

Math
FunctionsFill in the blanks.
The exponential function given by f(x) = e is called the ---Select- base and its approximate value is
---Select--- function, and the base e is called the (Round your answer to five decimal places).
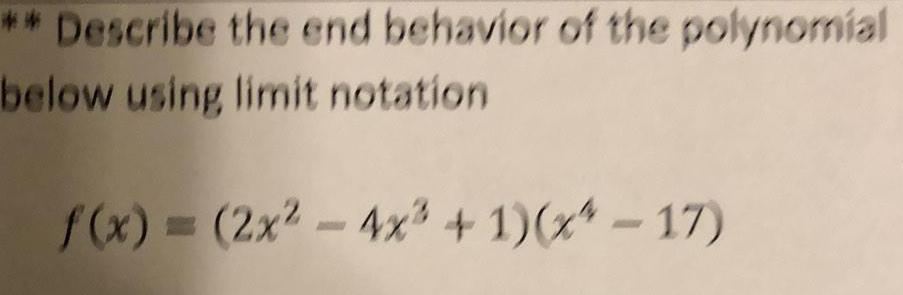
Math
FunctionsDescribe the end behavior of the polynomial below using limit notation
f(x) = (2x² - 4x³ + 1)(x²-17)

Math
FunctionsYour car radiator can hold 20 liters of fluid. Many automotive stores sell jugs of pure antifreeze, but some also sell jugs of antifreeze that have been premixed with water. Suppose you buy a jug of 30% antifreeze mixture as well as a jug of pure antifreeze. How many liters of each jug must you use to make enough of a 89.5% mixture to fill your radiator?

Math
FunctionsFor each pair of functions f and g below, find f(g(x)) and g (f(x)).
Then, determine whether fand g are inverses of each other.
Simplify your answers as much as possible.
(Assume that your expressions are defined for all .x in the domain of the composition.
You do not have to indicate the domain.)
(a) f(x) = 3x
g(x) = x/3
f(g(x)) =
g(f(x)) =
f and g are inverses of each other
f and g are not inverses of each other
(b) f(x) = 2x + 5
g(x) =x+5/2
f(g(x)) = 0
g(f(x)) = 0
f and g are inverses of each other
f and g are not inverses of each other

Math
FunctionsLet y = 2(x-4)^2-8.
Part A: Is the given relation a function? Is it one-to-one? Explain completely. If it is not one-to-one, determine a possible restriction on the domain such that the relation is one-
to-one.

Math
FunctionsFind the domain and the range of the given relation.
{(0,-5), (-4,1), (9,5), (5,9)}
The domain is. (Use a comma to separate answers as needed.)
The range is. (Use a comma to separate answers as needed.)

Math
FunctionsDescribe the transformation(s) of g (z) = (x+4)²-3 from its parent function of f(x) = x²
left 4, up 3
left 4 down 3
right 4 up 3
right 4, down 3
up 4, right 3
Oup 4, down 3

Math
FunctionsDescribe the transformation of f(x) = 10x which is given by g(x) = 103x.
A) g(x) is shrunk horizontally by a factor of 1/3 compared to f(x).
B) g(x) is stretched horizontally by a factor of 3 compared to f(x).
C) g(x) is shrunk vertically by a factor of 1/3 compared to f(x).
D) g(x) is stretched vertically by a factor of 3 compared to f(x).
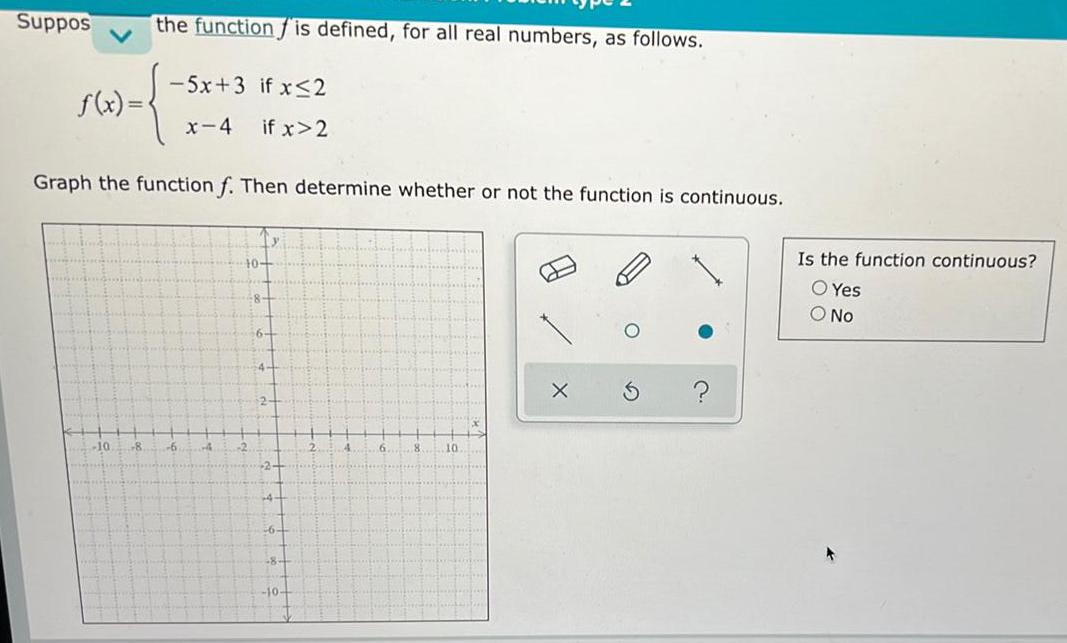
Math
FunctionsSuppose the function is defined, for all real numbers, as follows.
-5x+3 if x≤2
f(x)= { }
x-4 if x>2
Graph the function f. Then determine whether or not the function is continuous.
Is the function continuous?
Yes
No

Math
FunctionsWrite the function f(x) = |-4x + 36| as a piecewise-defined function.
A. f(x) =4x - 36, if x ≤ 9
-4x + 36, if x >9
B. f(x) = -4x + 36, if x < 9
4x - 36, if x > 9
C. f(x) =4x − 36, if x ≤ -9
-4x + 36, if x>-9
D. f(x) =-4x + 36, if x < −9
4x-36, if x > -9

Math
FunctionsDoes the function f(x) = 5e0.25x represent exponential growth, decay, or neither?
A) Exponential decay
B) Exponential growth
C) Neither
D) Impossible to determine with the information given.
Math
FunctionsAna is bowling. She pays $4 per game and $7 to rent
shoes. After three games, each additional game is free. Is the total
cost to bowl a function of the number of games played? Use a table
or graph to help explain your answer.

Math
FunctionsAccording to the Mini-Lesson, which of the following are TRUE regarding f(x) = a(b)? Check all that
apply. Assume a > 0.
The Horizontal Asymptote is the line y = 0.
The Domain of the exponential functions is All Real Numbers.
The Range of the exponential functions is All Real Numbers.
The Domain of the exponential functions is > 0.
The Range of the exponential functions is f(x) > 0.
The Horizontal Asymptote is the line a
The Horizontal Asymptote is the point (0, a).
Math
FunctionsConsider the following relation.
y = x + 1
Find the domain and range of the Inverse. Express your answer in Interval notation.
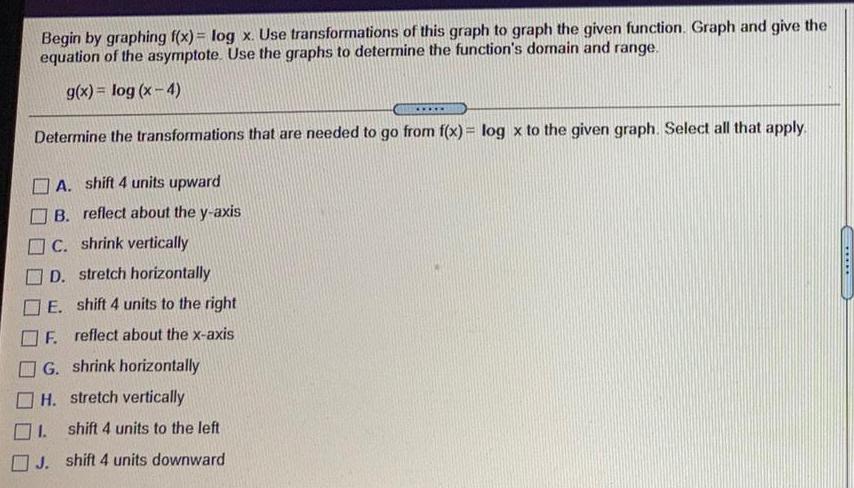
Math
FunctionsBegin by graphing f(x) = log x. Use transformations of this graph to graph the given function. Graph and give the equation of the asymptote. Use the graphs to determine the function's domain and range.
g(x) = log (x-4)
Determine the transformations that are needed to go from f(x) = log x to the given graph. Select all that apply.
A. shift 4 units upward
B. reflect about the y-axis
C. shrink vertically
D. stretch horizontally
E. shift 4 units to the right
F. reflect about the x-axis
G. shrink horizontally
H. stretch vertically
1. shift 4 units to the left
J. shift 4 units downward

Math
FunctionsLet A = f(r) be the area of a circle with radius r and r = h(t) be the radius of the circle at
time t.
Which of the following statements correctly provides a practical interpretation of the composite function f(h(t)) ? Select all that apply if more than one is appropriate.
A. The area of the circle which at time t has radius h(t) .
B. The length of the radius of a circle with area A = f(r) at time t.
C. The area of the circle at time t.
D. The length of the radius at time t.
E. At what time t the radius will be r = h(t).
F. At what time t the area will be A = f(r).
G. None of the above


Math
FunctionsConsider the following relation.
y=x+1
Find four points contained in the inverse. Express your values as an integer or simplified fraction.