Quadratic equations Questions and Answers

Math
Quadratic equationsList the roots of the parabola: y = 4x² + 8x - 2
In other words, list the solutions of the equation: 0 = 4x² + 8x - 2
Your answers must be in exact form, do not give their decimal values.
Separate multiple roots with a comma.

Math
Quadratic equationsThe temperature T, in degrees Fahrenheit, of a person during an illness is given by the function T(t) = 6t/t^2+1+98.6, where t= time, in hours. Find the interval over which the temperature was over 100⁰.
Math
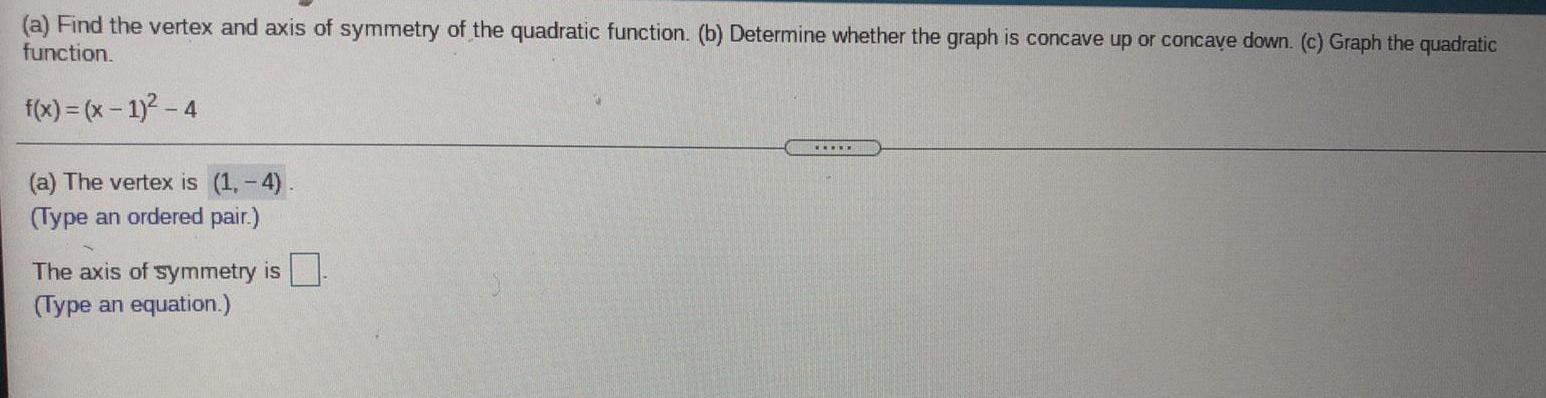
Quadratic equations(a) Find the vertex and axis of symmetry of the quadratic function. (b) Determine whether the graph is concave up or concave down. (c) Graph the quadratic function.
f(x) = (x - 1)² - 4
(a) The vertex is ().
(Type an ordered pair.)
The axis of symmetry is.
(Type an equation.)

Math
Quadratic equationsSolve the following quadratic inequality.
x2+5x+4≥0
Submit your answer by dragging the movable blue
points on the number line. For an interval that
extends to +∞ or -∞o move the blue points to
the right or left end of the number line (shown as a
dashed line). You can select whether each
endpoint of your chosen interval(s) is open or
closed by sliding the respective orange switches up
or down. Note that the blue line segment above
the number line indicates the interval(s) you have
chosen and whether the endpoints are open or
closed.
Math
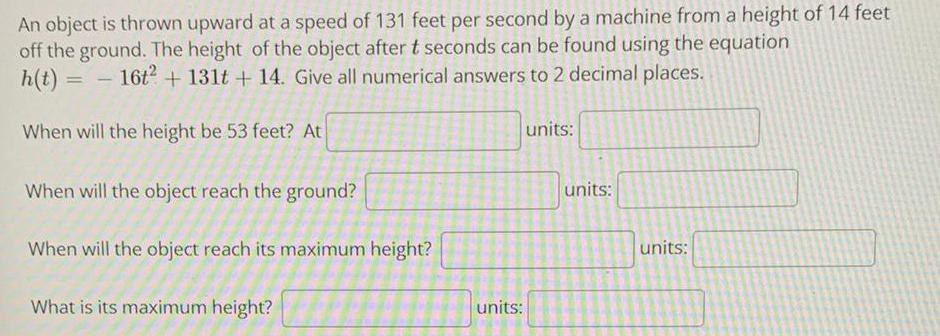
Quadratic equationsAn object is thrown upward at a speed of 131 feet per second by a machine from a height of 14 feet off the ground. The height of the object after t seconds can be found using the equation h(t) = 16t2 + 131t+ 14. Give all numerical answers to 2 decimal places.
When will the height be 53 feet? At units:
When will the object reach the ground? units:
When will the object reach its maximum height? units:
What is its maximum height? units:
Math
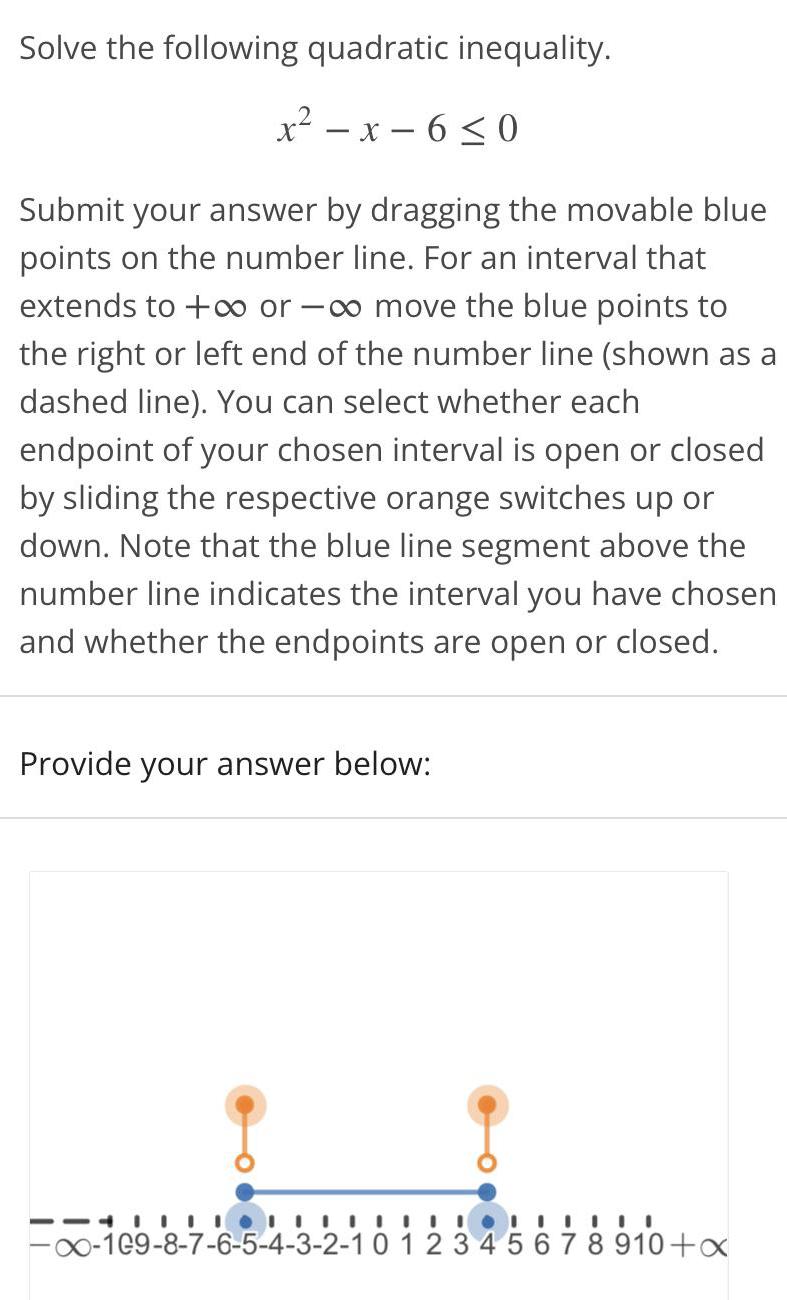
Quadratic equationsSolve the following quadratic inequality.
x²-x-6≤0
Submit your answer by dragging the movable blue
points on the number line. For an interval that
extends to +∞ or -∞o move the blue points to
the right or left end of the number line (shown as a
dashed line). You can select whether each
endpoint of your chosen interval is open or closed
by sliding the respective orange switches up or
down. Note that the blue line segment above the
number line indicates the interval you have chosen
and whether the endpoints are open or closed.


Math
Quadratic equationsAbigail has $30.00 to buy groceries. She needs to buy some apples, some bananas, and 3 pounds of potatoes. Fuji apples are $1.79 a pound, bananas are $0.36 each, and potatoes are $2.99 for a 3 lb. bag. If a represents the number of pounds of apples Abigail buys and b represents the number of bananas she buys, which expression represents the amount of change she receives after her purchases?
30.00-a-b
1.79a +0.36b+ 2.99
30.00-(1.79a +0.36b+ 2.99)
30.00+ (1.79a + 0.36b+ 2.99)

Math
Quadratic equationsA quadratic function f(x) is hidden from view. You must find all intervals where
f(x) is increasing. Choose the form of the quadratic function f(x) that you would
like to see in order to answer the question most efficiently.
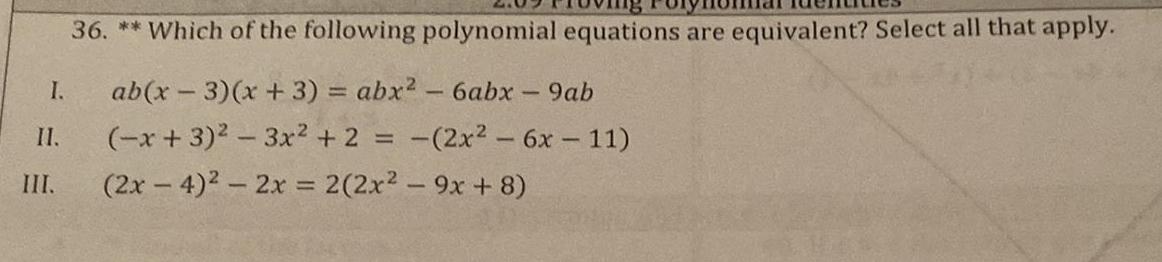
Math
Quadratic equationsWhich of the following polynomial equations are equivalent? Select all that apply.
I.ab(x − 3)(x + 3) = abx² - 6abx - 9ab
II.(-x+3)² - 3x² + 2 = -(2x² - 6x - 11)
III.(2x-4)² - 2x = 2(2x² - 9x + 8)

Math
Quadratic equationsUse the Intermediate Value Theorem to determine whether the polynomial function has a real zero between the given integers.
f(x) = 8x² + 2x³+ 9x - 9; between -2 and -1

Math
Quadratic equationsSolve for x in x2 + 5x-6 = 0 using the Quadratic
Formula.
x = 5,6
x = 2,3
x=1, -6
x = -2, -3
x = -1, -6

Math
Quadratic equationsFranco borrows a total of $5,000 in student loan from two lenders. One charges 4.1% simple interest and the other charges 6.1% simple interest. He is not required to pay off the principal for 3 yr. However, at the end of 3 yr, he will owe a total of $825.00 for interest from both loans. How much did he borrow from each lender?
Select one:
a. She borrowed $1,100 at 4.1% and $3,900 at 6.1%.
b. She borrowed $3,900 at 4.1% and $1,100 at 6.1%.
c. She borrowed $1,500 at 4.1% and $3,500 at 6.1%.
d. She borrowed $3,500 at 4.1% and $1,500 at 6.1%.

Math
Quadratic equationsConsider the following equation 28x²+28x + 7 = 0.
(a) Solve the equation by completing the square.
NOTE: Enter your solutions exactly. If there is only one solution, enter it twice.
(b) Solve the equation using the quadratic formula and give the
values for b and e given that a =28.
NOTE: Enter your solutions exactly. If there is only one solution, enter it twice.

Math
Quadratic equationsWithout solving, say whether the equation (x + 4)² = 19
has two solutions, one solution, or no solution.
The equation has
because

Math
Quadratic equationsGiven a polynomial that has zeros of -1, 7i, and -7i and has a value of 1000 when x = 1. Write the polynomial in standard form ax + bxn-1+. Answer using reduced fractions when necessary. ....





Math
Quadratic equationsDecide whether the following statement is true or false.
The graph of f(x) = 4x² + 5x - 7 opens up.
Choose the correct answer below.
False
True
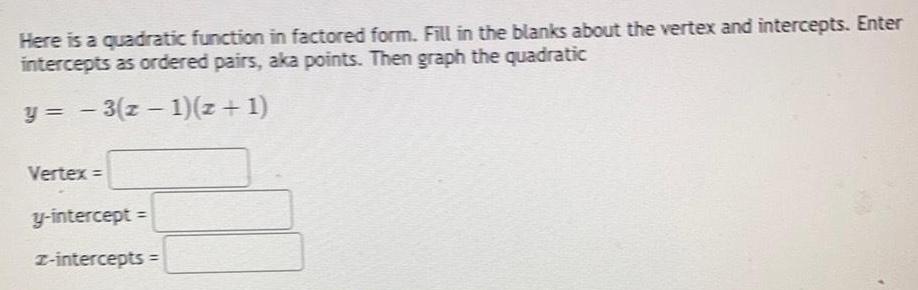
Math
Quadratic equationsHere is a quadratic function in factored form. Fill in the blanks about the vertex and intercepts. Enter intercepts as ordered pairs, aka points. Then graph the quadratic
y = -3(z − 1)(z + 1)
Vertex =
y-intercept =
I-intercepts=
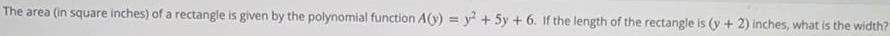
Math
Quadratic equationsThe area (in square inches) of a rectangle is given by the polynomial function A(y) = y² + 5y + 6. If the length of the rectangle is (y + 2) inches, what is the width?

Math
Quadratic equations3. Evin is walking home from the museum. She starts 38 blocks from home and walks 2 blocks each minute.
Evin's distance from home is a function of the number of minutes she has been walking.
(a) Which variable is independent and which variable is dependent in this scenario?
(b) Fill in the table below for a variety of time values.
Time, 1, in minutes
Distance from home, D, in blocks
(c) Determine an equation relating the
distance, D, that Evin is from home as a
function of the number of minutes, 1, that
she has been walking.
0
1
5
10
(d) Determine the number of minutes, t, that it
takes for Evin to reach home.

Math
Quadratic equationsUse z scores to compare the given values.
The tallest living man at one time had a height of 240 cm. The shortest living man at that time had a height
of 65.6 cm Heights of men at that time had a mean of 171.12 cm and a standard deviation of 7.39 cm.
Which of these two men had the height that was more extreme?
Since the z score for the tallest man is z= and the z score for the shortest man is z=
man had the height that was more extreme.
(Round to two decimal places)
the

Math
Quadratic equationsSolve the equation. List both the exact solution and its approximation rounded to two decimal places. (Enter your answers as a
comma-separated list. If an answer does not exist, enter DNE.)
12x²136x + 285 = 0
Exact solution: x =
Approximate solution: x =

Math
Quadratic equationsks. Diagrams are not to scale unless otherwise stated.
2. The coordinates of the endpoints of ABC are
A(-8,-2) and C(16,6). What are the coordinates of
point B, such that AB:BC is 3:5?
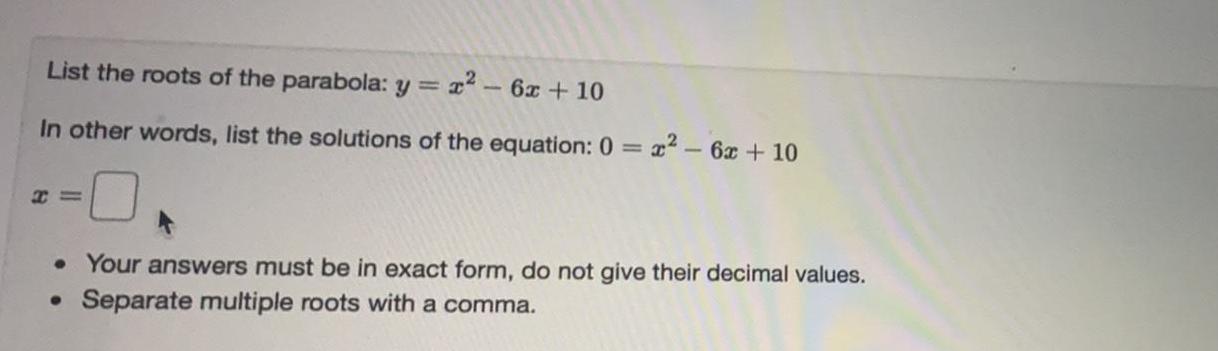
Math
Quadratic equationsList the roots of the parabola: y = x² - 6x + 10
In other words, list the solutions of the equation: 0= x² - 6x + 10
H=
• Your answers must be in exact form, do not give their decimal values.
• Separate multiple roots with a comma.

Math
Quadratic equationsTwo long distance runners began an 18 3/4-mile run. They ran uphill for 5 5/8 miles, downhill 7 1/3 miles, and the rest of the course was level. Find the distance of the level portion of the course.

Math
Quadratic equationsExercise #3: The graph of the function y=x²-4x+1 is shown below.
(a) State this function's y-intercept.
(b) Between what two consecutive integers does the larger x-
intercept lie?
(c) Draw the horizontal line y=-2 on this graph.
(d) Using these two graphs, find all values of x that solve
the equation below:
x²-4x+1=-2

Math
Quadratic equationsThe Royal Fruit Company produces two types of fruit drinks. The first type is 70% pure fruit juice, and the second type is 95% pure fruit juice. The company is attempting to produce a fruit drink that contains 85% pure fruit juice. How many pints of each of the two existing types of drink must be used to make 180 pints of a mixture that is 85% pure fruit juice?
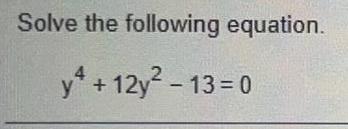

Math
Quadratic equationsA ball is launched from a 1128.32-foot tall platform. The equation for the ball's height h at time t seconds after launch is
h(t) = − 16t² + 6.4t + 1128.32
where h is in feet. When does the object strike the ground?

Math
Quadratic equationsA box with an open top has a square base and four sides of equal height. The volume of the box is 144 ft³. If the surface area is 160 ft^2, find the dimensions of the box.

Math
Quadratic equationsPlease number your responses to the questions as they are shown (1 and 2).
Tanya is given the graphs of the following functions. The functions f(x) and g(x) are linear, and the
function s(x) is quadratic.
f(x) = 3x - 8
g(x) = -2x + 5
s(x) = 4x² - 9x + 2
Tanya is then asked to find the graph of (f .g)(x) and the graph of (g.s)(x). For each combined
function, she is given four options to choose from.
1. What clues will help Tanya identify the correct graph of (f. g)(x)
2. What clues will help Tanya identify the correct graph of (g.s)(x)

Math
Quadratic equationsWe are standing on the top of a 512 feet tall building and launch a small object upward. The object's
vertical position, measured in feet, after t seconds is h(t) = -16t² +64t + 512. What is the highest
point that the object reaches?
feet

Math
Quadratic equationsDetermine if the following sets of quadratics are equivalent. Choose true or false.
x-10x+14 = 0 and (2x-10)2 =156
(x-10)² = 68 and ² - 20x=-32
x² - 6x=247 and (x-3)² = 256
(x + 5)² = 65 and x² = 90 - 10x

Math
Quadratic equationsUse the long division method to find the result when 3x³ + 5x² - 15x+7 is divided by x - 1.
Math
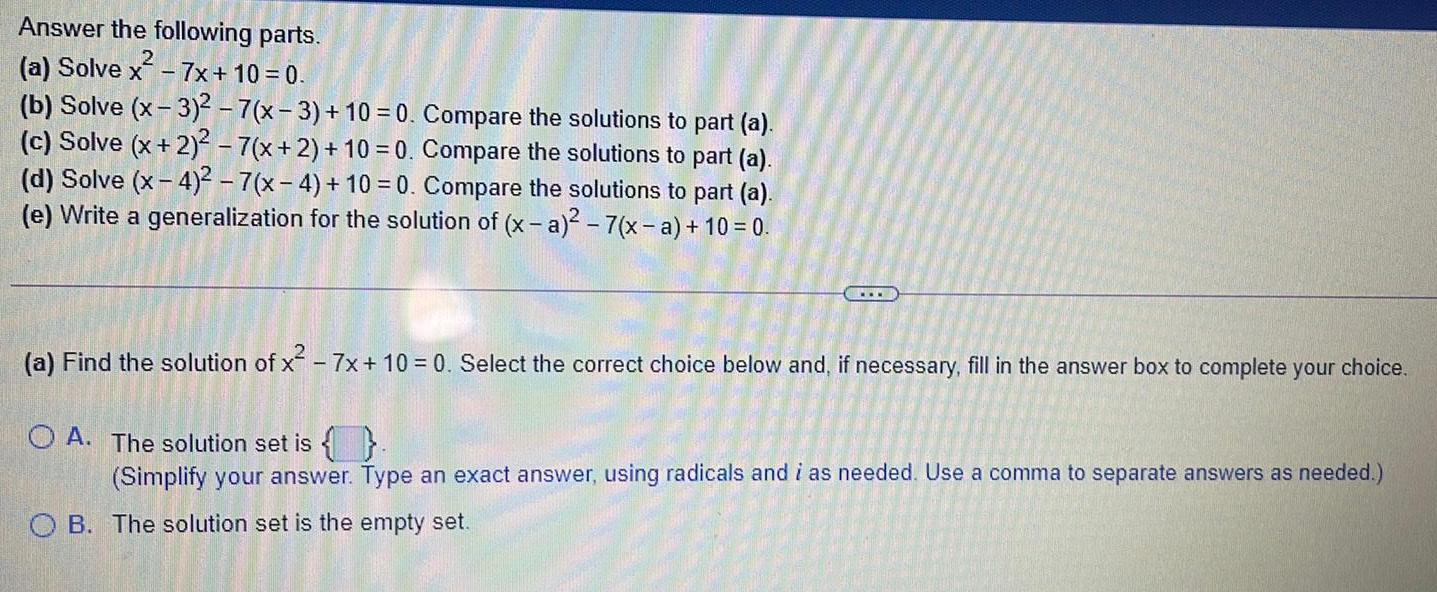
Quadratic equationsAnswer the following parts.
(a) Solve x² - 7x + 10 = 0.
(b) Solve (x-3)² - 7(x-3) + 10 = 0. Compare the solutions to part (a).
(c) Solve (x + 2)² - 7(x + 2) + 10 = 0. Compare the solutions to part (a).
(d) Solve (x-4)² - 7(x-4) + 10 = 0. Compare the solutions to part (a).
(e) Write a generalization for the solution of (x-a)² - 7(x-a) + 10 = 0.
Math
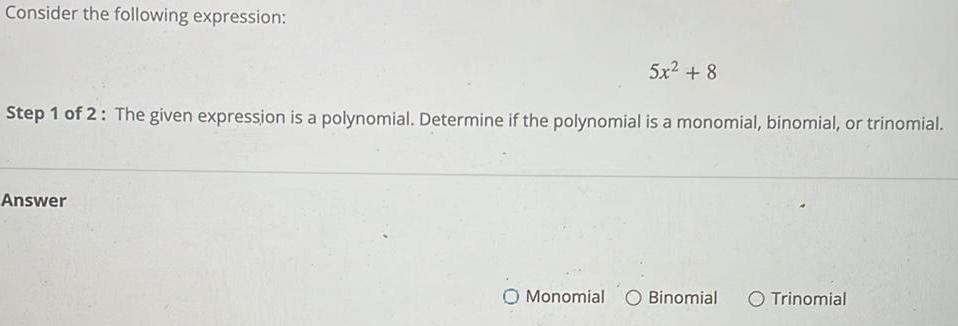
Quadratic equationsConsider the following expression:
5x2 +8
Step 1 of 2: The given expression is a polynomial. Determine if the polynomial is a monomial, binomial, or trinomial.

Math
Quadratic equationsFor the quadratic function f(x) = 2x² + 24x + 9,
(a) Use completing the square to write the function in the form f(x)= a(x-h)²+k.
(b) Use your answer to (a) to identify the vertex.

Math
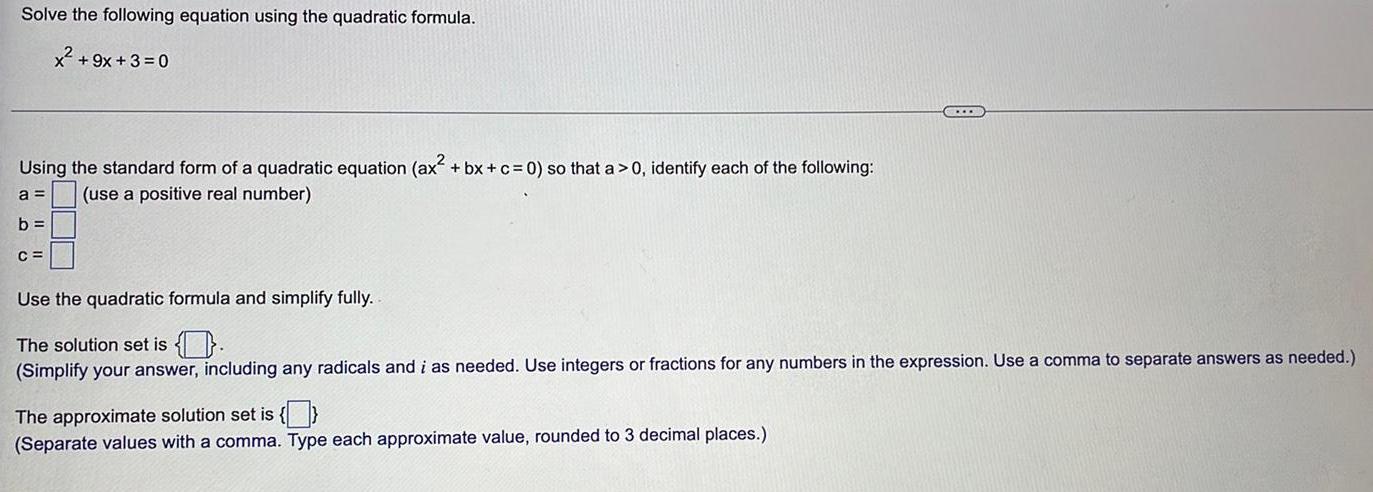
Quadratic equationsSolve the following equation using the quadratic formula.
x² +9x+3=0
Using the standard form of a quadratic equation (ax² +bx+c= 0) so that a > 0, identify each of the following:
a= (use a positive real number)
b =
C =
Use the quadratic formula and simplify fully.
The solution set is.
(Simplify your answer, including any radicals and i as needed. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.)
The approximate solution set is {}
(Separate values with a comma. Type each approximate value, rounded to 3 decimal places.)

Math
Quadratic equationsSolve using elimination.
x^2 + y2 = 41
x^2-y2= 9
x = 5, y = -4; x = 5, y = 4 or (5,-4), (5, 4)
x = 5, y = 4; x = 4, y = 5; x = -5, y = -4; x = -4, y = -5 or (5, 4), (4, -5), (-5, -4), (-4, -5)
x = 5, y = 4; x = -5, y = 4; x = 5, y = -4; x = -5, y = -4 or (5, 4), (-5, 4), (5,-4), (-5, -4)
x = -5, y = -4; x = -4, y = -5 or (-5, -4), (-4,-5)

Math
Quadratic equationsThe equation y = (-16t-2)(t-1) represents the height in feet of a beach ball thrown by a child as a function of time, t, in seconds.
1. Find the zeros of the function. Explain or show your reasoning.
2. What do the zeros tell us in this situation? Are both zeros meaningful?
3. From what height is the beach ball thrown? Explain or show your reasoning.

Math
Quadratic equationsDetermine the type and number of solutions for the equation.
x2 + 3x=8
Choose the type and number of solutions.
A. Imaginary solutions, 2
B. Rational solutions, 2
C. Irrational conjugates, 2
D. Repeated solution, 1
Math
Quadratic equationsSolve the equation x² + 9x - 30 using the Quadratic Formula.
Give your answers as two separate numbers in exact form.

Math
Quadratic equationsIf a quadratic function has no real solutions, then what can be concluded about the discriminant of the function?
The discriminant must be positive.
The discriminant must be zero.
The discriminant could be positive or negative.
The discriminant must be negative.

Math
Quadratic equationsIn trying to factor 3x² - 7x - 6, Tina determine that the proper numbers for multiplying and adding were -9 and +2. Which expression would be the next step?
(x-9)(x + 2)
(3x - 9)(3x + 2)
(3x-9)(x+2)/3
(3x-9)(3x+2)/3