Functions Questions and Answers
Math
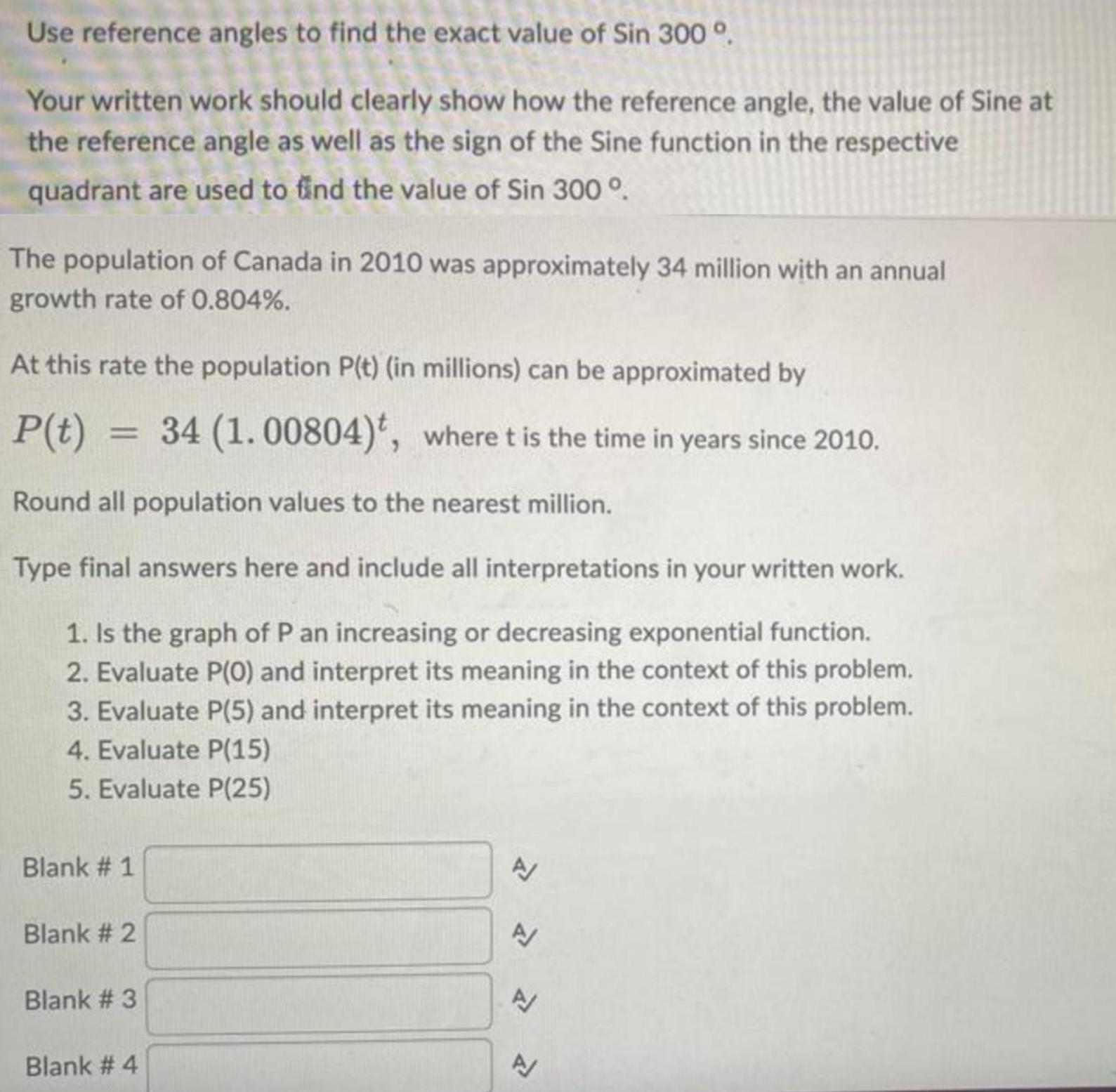
FunctionsUse reference angles to find the exact value of Sin 300 °.
Your written work should clearly show how the reference angle, the value of Sine at the reference angle as well as the sign of the Sine function in the respective quadrant are used to find the value of Sin 300 °.
The population of Canada in 2010 was approximately 34 million with an annual growth rate of 0.804%.
At this rate the population P(t) (in millions) can be approximated by
P(t) = 34 (1.00804)t, where t is the time in years since 2010.
Round all population values to the nearest million.
Type final answers here and include all interpretations in your written work.
1. Is the graph of P an increasing or decreasing exponential function.
2. Evaluate P(0) and interpret its meaning in the context of this problem.
3. Evaluate P(5) and interpret its meaning in the context of this problem.
4. Evaluate P(15)
5. Evaluate P(25)

Math
FunctionsDescribe the transformations to the parent function. Check all boxes that apply.
y = (x + 2)²
Reflects across the x-axis (open down)
shifts right 2
shifts left 2
shifts up 2
shifts down 2
shifts right 3
shifts left 3
shifts up 3
shifts down 3

Math
FunctionsStarting with the graph of f(x) = 3^x, write the equation of the graph that results from
(a) shifting f(x) 6 units upward.
(b) shifting f(x) 7 units to the left.
(c) reflecting f(x) about the y-axis.

Math
FunctionsThe function D(p) gives the number of items that will be demanded when the price is p. The production cost, C'(x) is the cost of producing x items. To determine the cost of production when the price is $10, you would:
Evaluate D(C(10))
Solve D(C(x)) = 10
Evaluate C(D(10))
Solve C(D(p)) = 10
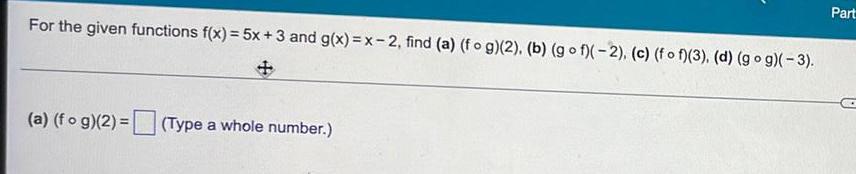
Math
FunctionsFor the given functions f(x) = 5x + 3 and g(x)=x-2, find (a) (fog)(2). (b) (gof)(-2), (c) (fof)(3), (d) (gog)(-3).
(a) (fog)(2)=

Math
FunctionsThe cost, in millions of dollars, of a 30-second television ad during an annual television event in the years 2000-2010 can be approximated by C(t) = 0.16t+ 1.3 million dollars (0 ≤ t ≤ 10). = 0 represents 2000.) What was the average cost of an ad in the event during the given period?

Math
FunctionsThe number of new members joining Facebook each year in the period from 2005 to the middle of 2008 can be modeled by m(t)
12t² - 20t + 10 million members per year
(0 ≤ t ≤ 3.5),
where t is time in years since the start of 2005.+ What was the average number of new members joining Facebook each year from the start of 2005 to the start of 2007?

Math
FunctionsFind the following information for f(x) = x²-x-12 (
(Hint: Do not forget to factor before you do anything else)
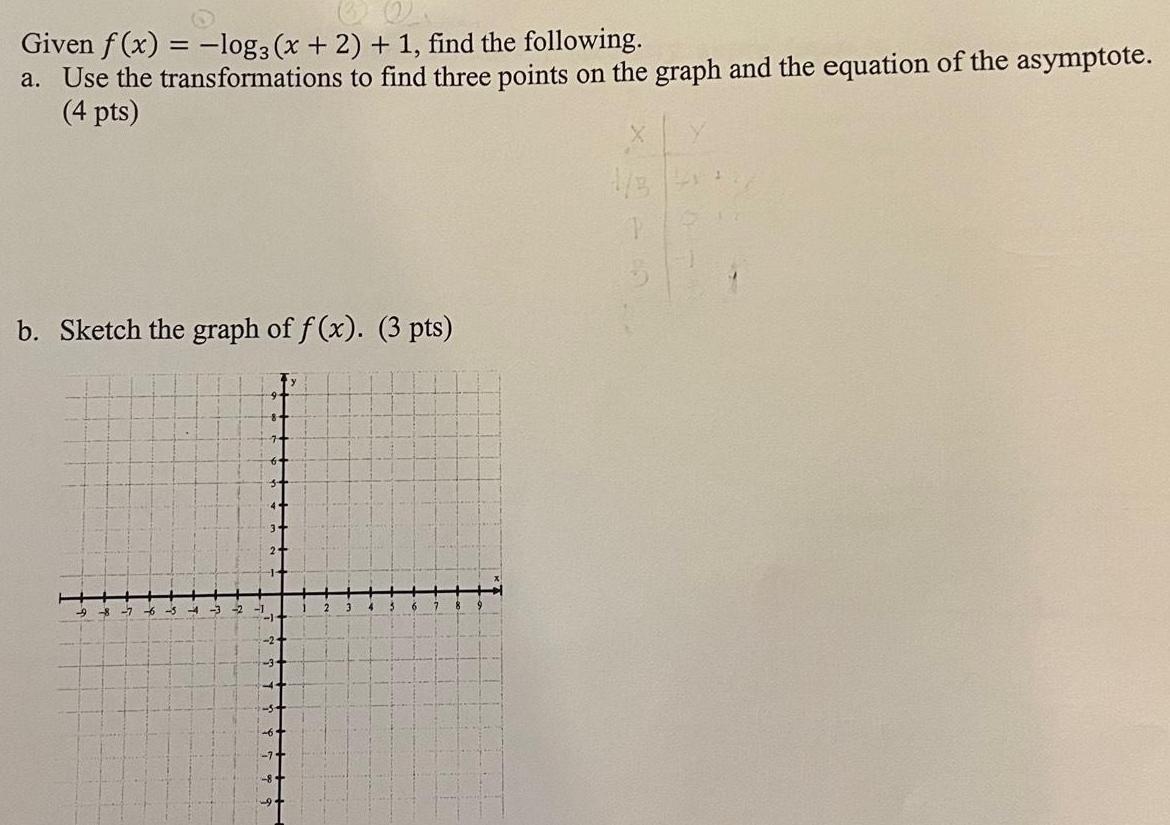
Math
FunctionsGiven f(x) = -log3 (x + 2) + 1, find the following. a. Use the transformations to find three points on the graph and the equation of the asymptote. b. Sketch the graph of f(x).
![Let f(x) = ²-3t + 2 dt. We'll take the domain of ƒ to be a 20.
(a) Find the intervals of increase or decrease of f(x) and any local extrema.
(b) Find the intervals of concavity of f(x) and any points of inflection.
(c) Find the absolute max and min of f(x) on the interval [0,3].](https://media.kunduz.com/media/sug-question/raw/77564311-1660484956.3946884.jpeg?w=256)
Math
FunctionsLet f(x) = ²-3t + 2 dt. We'll take the domain of ƒ to be a 20.
(a) Find the intervals of increase or decrease of f(x) and any local extrema.
(b) Find the intervals of concavity of f(x) and any points of inflection.
(c) Find the absolute max and min of f(x) on the interval [0,3].
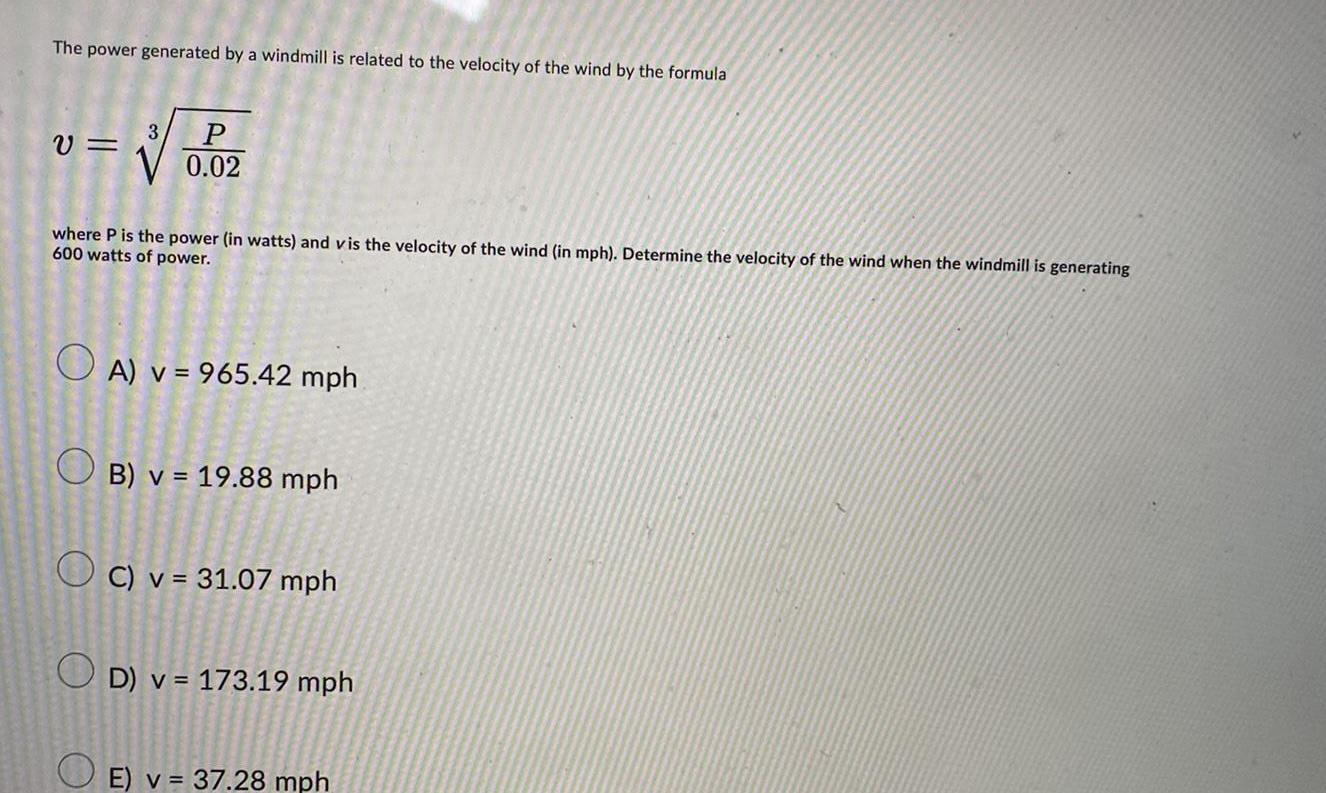
Math
FunctionsThe power generated by a windmill is related to the velocity of the wind by the formula
where P is the power (in watts) and vis the velocity of the wind (in mph). Determine the velocity of the wind when the windmill is generating
600 watts of power.
A) v = 965.42 mph
B) v = 19.88 mph
C) v = 31.07 mph
D) v = 173.19 mph
E) v = 37.28 mph

Math
FunctionsRefer to the graph of k(n) to complete the table of values. Determine the formula for the function k(n), then use words to describe the relationship between the input and output variables.
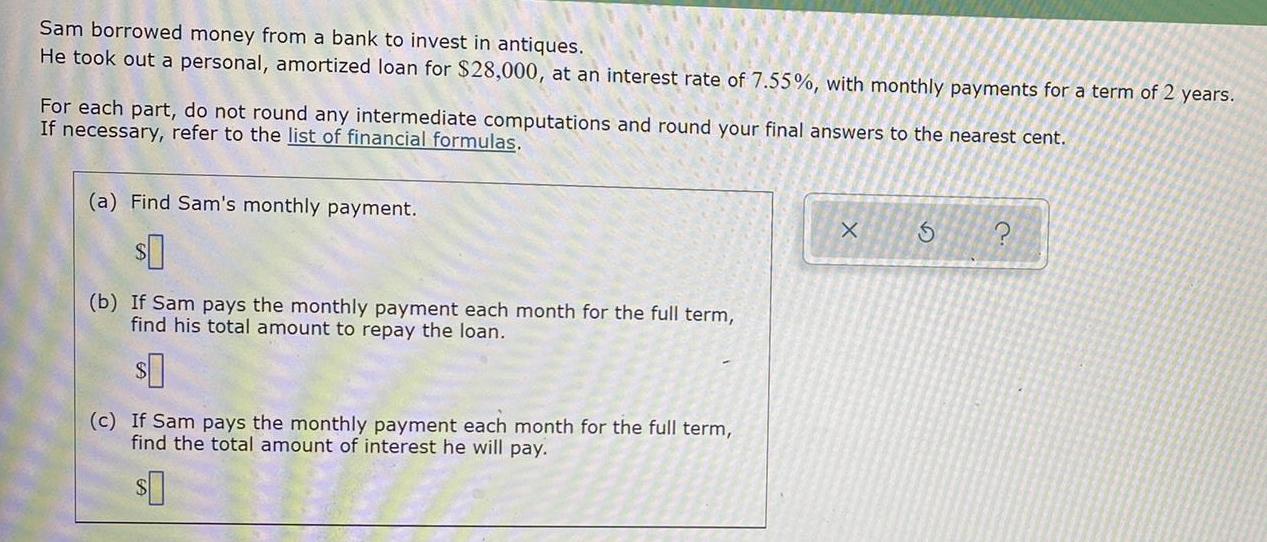
Math
FunctionsSam borrowed money from a bank to invest in antiques.
He took out a personal, amortized loan for $28,000, at an interest rate of 7.55%, with monthly payments for a term of 2 years.
For each part, do not round any intermediate computations and round your final answers to the nearest cent.
If necessary, refer to the list of financial formulas.
(a) Find Sam's monthly payment.
(b) If Sam pays the monthly payment each month for the full term, find his total amount to repay the loan.
(c) If Sam pays the monthly payment each month for the full term, find the total amount of interest he will pay.
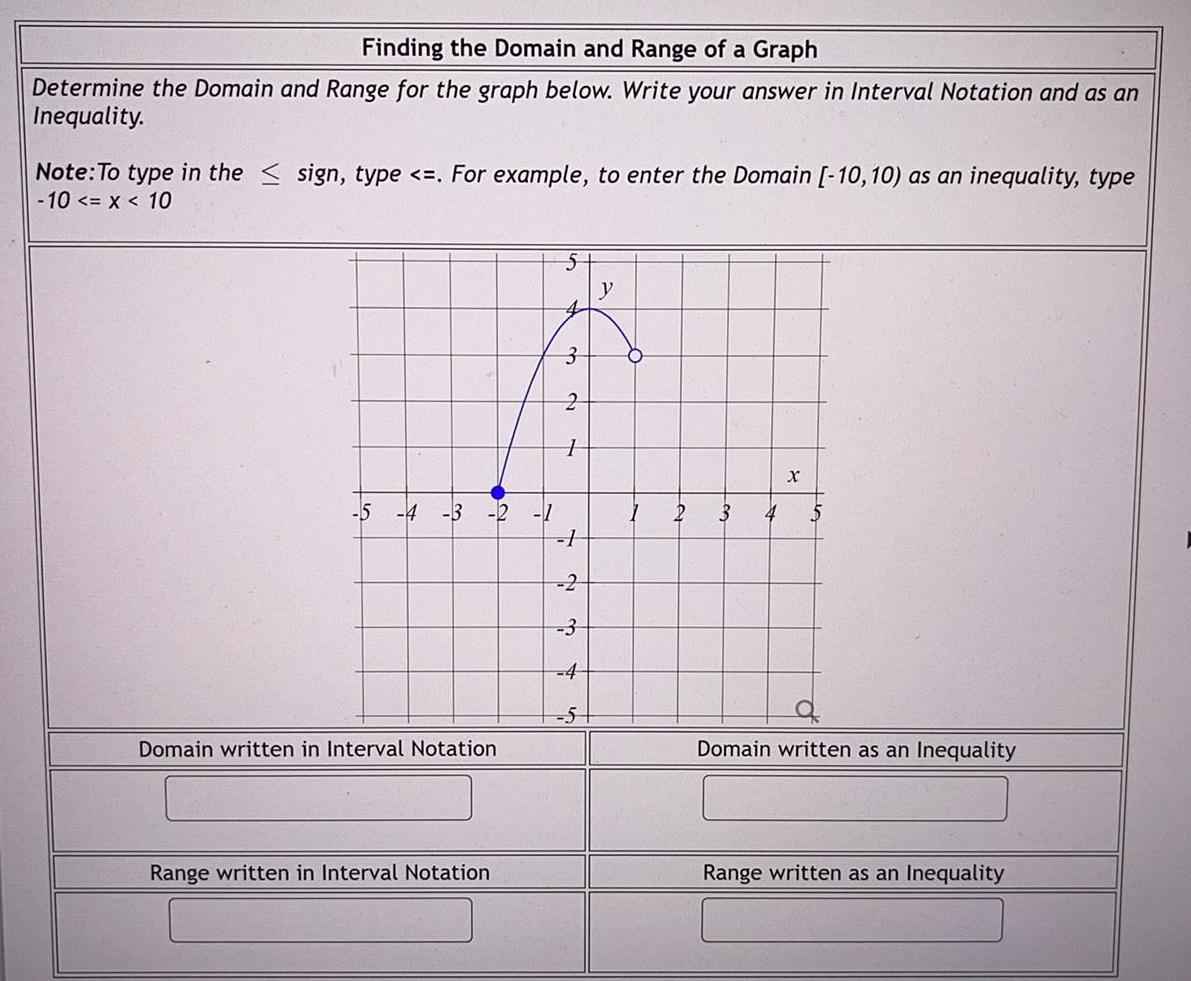
Math
FunctionsDetermine the Domain and Range for the graph below. Write your answer in Interval Notation and as an
Inequality.
-10 < = x < 10
-5 -4
-3 -2 -1
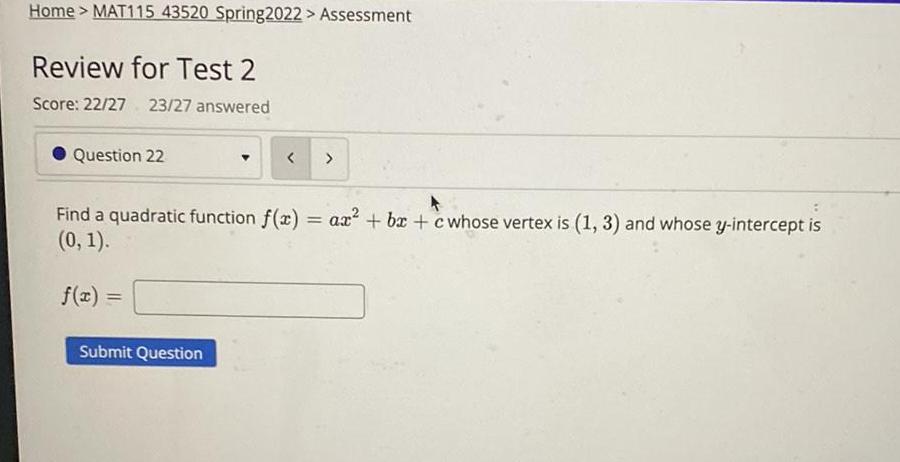
Math
FunctionsFind a quadratic function f(x) = ax²+bx+c whose vertex is (1, 3) and whose y-intercept is (0, 1).
f(x) =

Math
FunctionsThe following models describe wages for low-skilled labor.
p = -0.325x+5.8 demand model
p = 0.375x +3 supply model
where p represents the price of labor per hour and x is the number of workers
available in millions. Determine the equilibrium number of workers, in millions,
associated with the equilibrium wage per hour.
5 million workers @ $4.88 an hour
3 million workers @ $4.12 an hour
4.5 million workers @ $4.68 an hour
4 million workers @ $4.50 an hour
![Suppose g (z) = -(z − a)³ (z - b)²(z − 1)². Describe the graph of g (z)
a. The graph the x-axis at x = d.
b. The graph [zero2] the x-axis at x = b.
c. The graph [zero3] the x-axis at x = 1.
d. At the ends, the graph (end).](https://media.kunduz.com/media/sug-question/raw/77312392-1660470183.0140185.jpeg?w=256)
Math
FunctionsSuppose g (z) = -(z − a)³ (z - b)²(z − 1)². Describe the graph of g (z)
a. The graph the x-axis at x = d.
b. The graph [zero2] the x-axis at x = b.
c. The graph [zero3] the x-axis at x = 1.
d. At the ends, the graph (end).
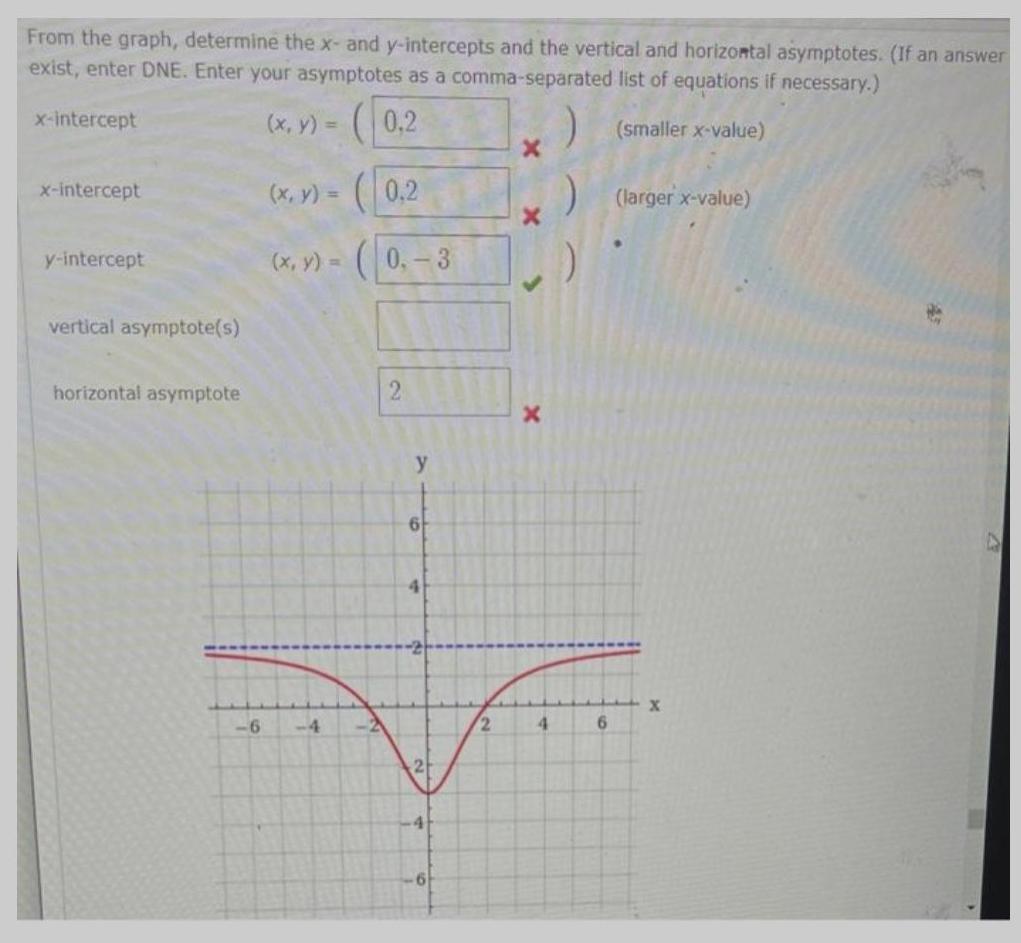
Math
FunctionsFrom the graph, determine the x- and y-intercepts and the vertical and horizontal asymptotes. (If an answer exist, enter DNE. Enter your asymptotes as a comma-separated list of equations if necessary.)
x-intercept (x, y) = (0,2 (smaller x-value)
x-intercept
y-intercept
vertical asymptote(s)
horizontal asymptote
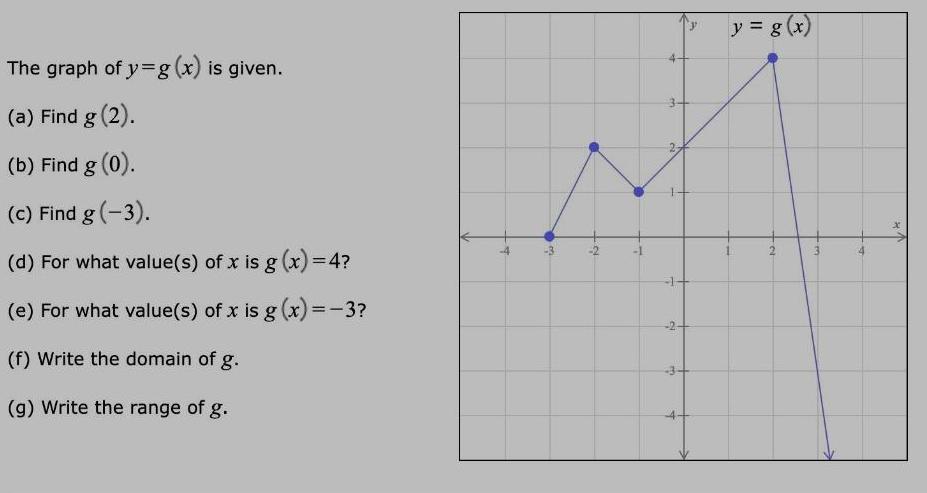
Math
FunctionsThe graph of y=g (x) is given.
(a) Find g (2).
(b) Find g (0).
(c) Find g (-3).
(d) For what value(s) of x is g (x)=4?
(e) For what value(s) of x is g(x)=-3?
(f) Write the domain of g.
(g) Write the range of g.
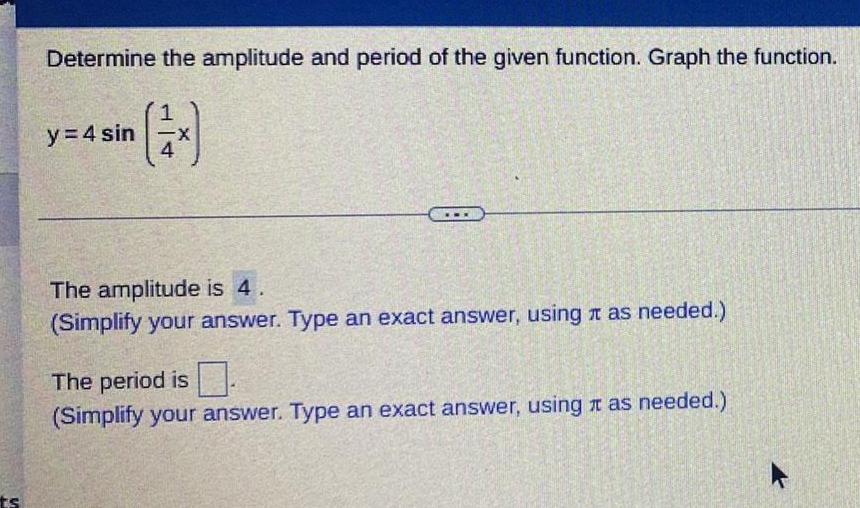
Math
FunctionsDetermine the amplitude and period of the given function. Graph the function.
y = 4 sin (x/4)
The amplitude is 4
The period is
Math
FunctionsA nut store normally sells cashews for $4.00 per pound and peanuts for $1.50 per pound. But at the end of the month the peanuts had not sold well, so, in order to sell 90 pounds of peanuts, the manager decided to mix the 90 pounds of peanuts with some cashews and sell the mixture for $2.50 per pound. How many pounds of cashews should be mixed with the peanuts to ensure no change in the revenue?
The manager should mix
pounds of cashews with the peanuts.

Math
FunctionsWhat are the solutions to x2-5x-14?
The x-intercepts are x = -7 and x = -2.
The x-intercepts are x = -7 and x = 2.
The x-intercepts are x = 7 and x = 2.
The x-intercepts are x = 7 and x = -2.

Math
FunctionsThe function H described by H(x)=2.75x+71.48 can be used to estimate the height, in centimeters, of a woman whose humerus (the bone from the elbow to the shoulder) is x cm long. Estimate the height of a woman whose humerus is 33.5 cm
long.
A. 107.73 cm
B. 40.73 cm
C. 20.645 cm
D. 163.605 cm
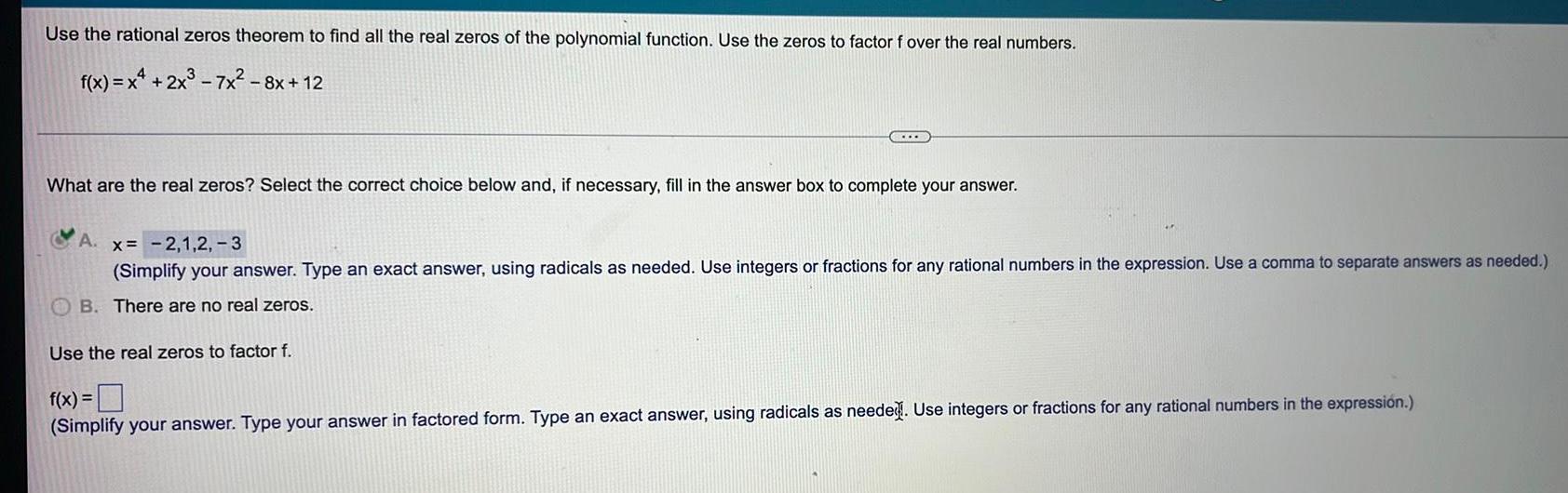
Calculus
FunctionsUse the rational zeros theorem to find all the real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
f(x) = x² + 2x³-7x² − 8x+12
...
What are the real zeros? Select the correct choice below and, if necessary, fill in the answer box to complete your answer.
A. x= -2,1,2,-3
(Simplify your answer. Type an exact answer, using radicals as needed. Use integers or fractions for any rational numbers in the expression. Use a comma to separate answers as needed.)
B. There are no real zeros.
Use the real zeros to factor f.
f(x) =
(Simplify your answer. Type your answer in factored form. Type an exact answer, using radicals as needed. Use integers or fractions for any rational numbers in the expression.)

Calculus
FunctionsComplete the sentence below.
If f is a polynomial function and x-5 is a factor of f, then f(5) =
If f is a polynomial function and x-5 is a factor of f, then f(5) =

Math
FunctionsThe graph to the right is obtained from the graph of g(x)=√x by applying several transformations. Describe the transformations and give the equation of the graph.
A. Translate g(x) unit(s) down. (Type a whole number.)
B. Translate g(x) 2 unit(s) up. (Type a whole number.)
C. No vertical translation is needed.
Give the equation of the graph.
(Type an equation.)
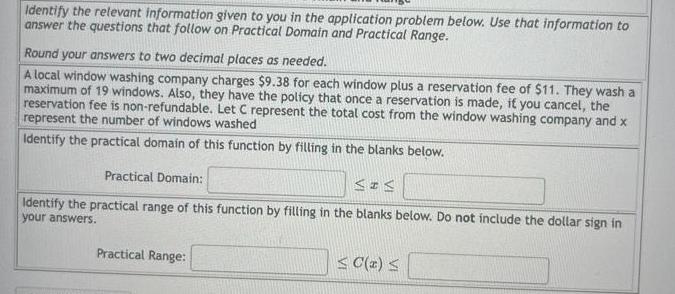
Math
FunctionsIdentify the relevant information given to you in the application problem below. Use that information to answer the questions that follow on Practical Domain and Practical Range.
Round your answers to two decimal places as needed.
A local window washing company charges $9.38 for each window plus a reservation fee of $11. They wash a maximum of 19 windows. Also, they have the policy that once a reservation is made, if you cancel, the reservation fee is non-refundable. Let C represent the total cost from the window washing company and x represent the number of windows washed
Identify the practical domain of this function by filling in the blanks below.
Practical Domain:
Identify the practical range of this function by filling in the blanks below. Do not include the dollar sign in your answers.
Practical Range:
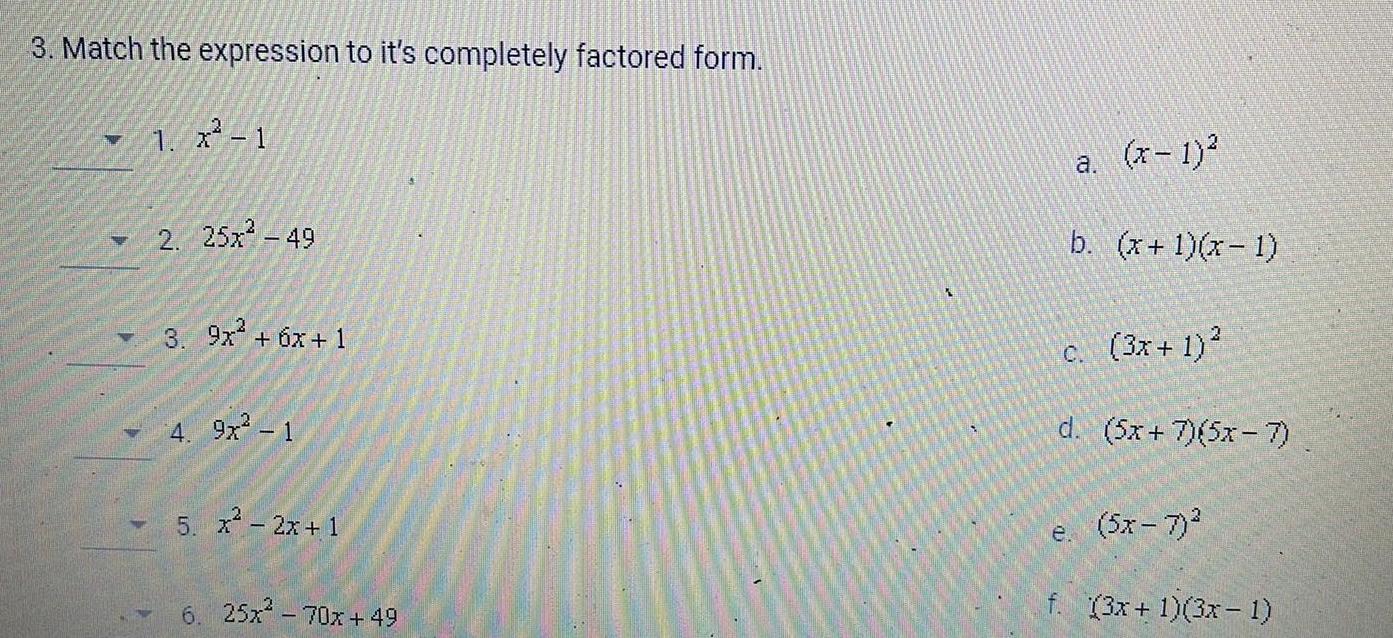
Math
Functions3. Match the expression to it's completely factored form.
1. x²-1
2. 25x² - 49
3. 9x² + 6x +1
4. 9x² - 1
5. x² - 2x + 1
6. 25x² - 70x+49
a. (x-1)²
b. (x + 1)(x-1)
c. (3x + 1)²
d. (5x+7)(5x-7)
e. (5x - 7)2
f. (3x + 1)(3x - 1)

Math
FunctionsWrite a polynomial f(x) that satisfies the given conditions. Express the polynomial with the lowest possible leading positive
integer coefficient.
Polynomial of lowest degree with lowest possible integer coefficients and zeros of 3i and 5-3i.
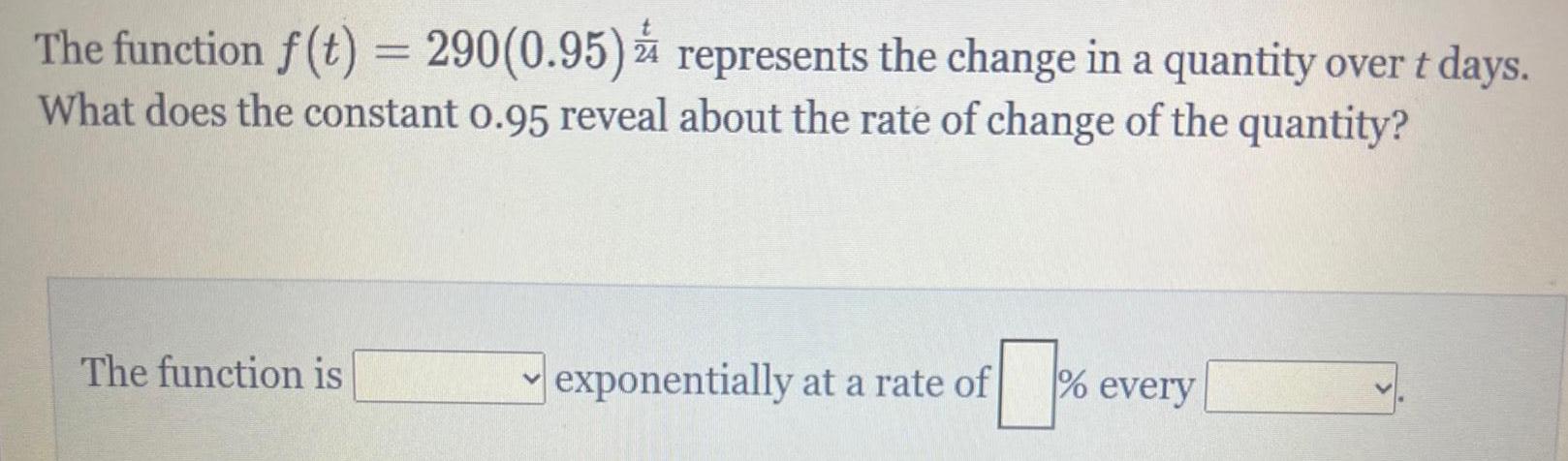
Math
FunctionsThe function f(t) = 290(0.95)t/24 represents the change in a quantity over t days.
What does the constant 0.95 reveal about the rate of change of the quantity?
The function is_____%
exponentially at a rate of _____% every______
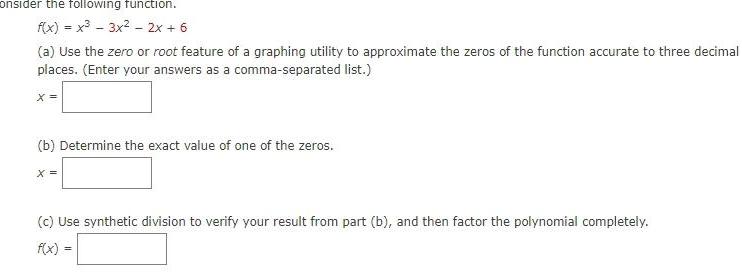
Math
Functionsonsider the following function.
f(x) = x³ 3x² - 2x + 6
(a) Use the zero or root feature of a graphing utility to approximate the zeros of the function accurate to three decimal
places. (Enter your answers as a comma-separated list.)
X =
(b) Determine the exact value of one of the zeros.
X =
(c) Use synthetic division to verify your result from part (b), and then factor the polynomial completely.
f(x)=

Math
FunctionsFind a possible formula for the polynomials with the given properties: f is third degree with f(-5) = 0, f(2)= 0, f(6) = 0 and f(3) = 5. f(x) =
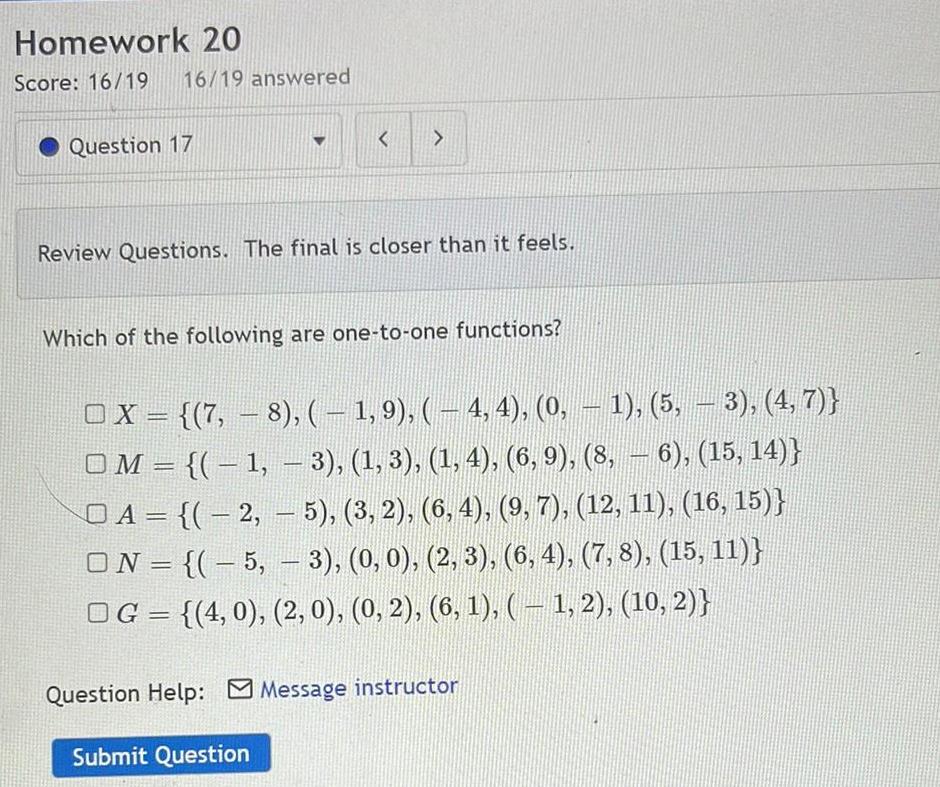
Math
FunctionsWhich of the following are one-to-one functions?
X= {(7, 8), ( – 1,9), ( – 4, 4), (0, – 1), (5, — 3), (4, 7)}
M = {( − 1, — 3), (1, 3), (1, 4), (6, 9), (8, — 6), (15, 14)}
A= {(2, — 5), (3, 2), (6, 4), (9, 7), (12, 11), (16, 15)}
N = {(-5, — 3), (0, 0), (2, 3), (6, 4), (7, 8), (15, 11)}
G = {(4,0), (2, 0), (0, 2), (6, 1), ( − 1, 2), (10, 2)}

Math
FunctionsWhich statement is true about the period of the parent sine function?
The period is because that is one full cycle of the graph.
The period is 2π because that is one full cycle of the graph.
The period is 27 because that is two full cycles of the graph.
The period is because from 0 to it is half of a full cycle.

Calculus
FunctionsConsider the following pair of parametric equations: x(t) =(1/2)t, y(t)= 2^t
a. If the domain of this pair of parametric equations is - 2≤t≤ 2:
i.What is the domain of x over this interval?
ii.What is the range of y over this interval?
b. Eliminate the parameter from this pair of parametric equations to express y as a function of x.

Math
FunctionsUse Descartes' Rule of Signs to determine the number of possible combinations of positive and negative
real zeros of
f(x) = 4x³ + 7x* + 102x³+174x²+ 50x-25
Also, use the Rational Root Theorem, the Remainder Theorem, and synthetic division to determine all roots and factors(linear and quadratic) of the polynomial. Answer the following questions in your analysis:
(a-d one point each)
a. Degree = b. # of zeros: c. Max. # of turns:

Math
FunctionsGive an expression for f(x) with leading coefficient 3, of degree 3, and having roots x = 6, x=2 + i, and x = 2-i.
• Your final answer should not contain any i's.
f(x) =__ is a polynomial of degree 3 with the given roots and leading coefficient.

Math
FunctionsGive an expression for f(x) using only Real-valued coefficients, having degree 4, passing through the point (-8,370), with roots a = -6, a = -9, and x = -2-i.
• Your final answer should not contain any i's.
f(x) = is a polynomial of degree. with the given roots and passes through (-8,370).

Math
FunctionsFor the following function, a) determine whether it is one-to-one; b) if it is one-to-one, find its inverse function.
f(x)=x+9
Is the given function a one-to-one function? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. Yes, the function is one-to-one. The inverse function is f(x) =
(Simplify your answer.)
B. No, the the function is not one-to-one.
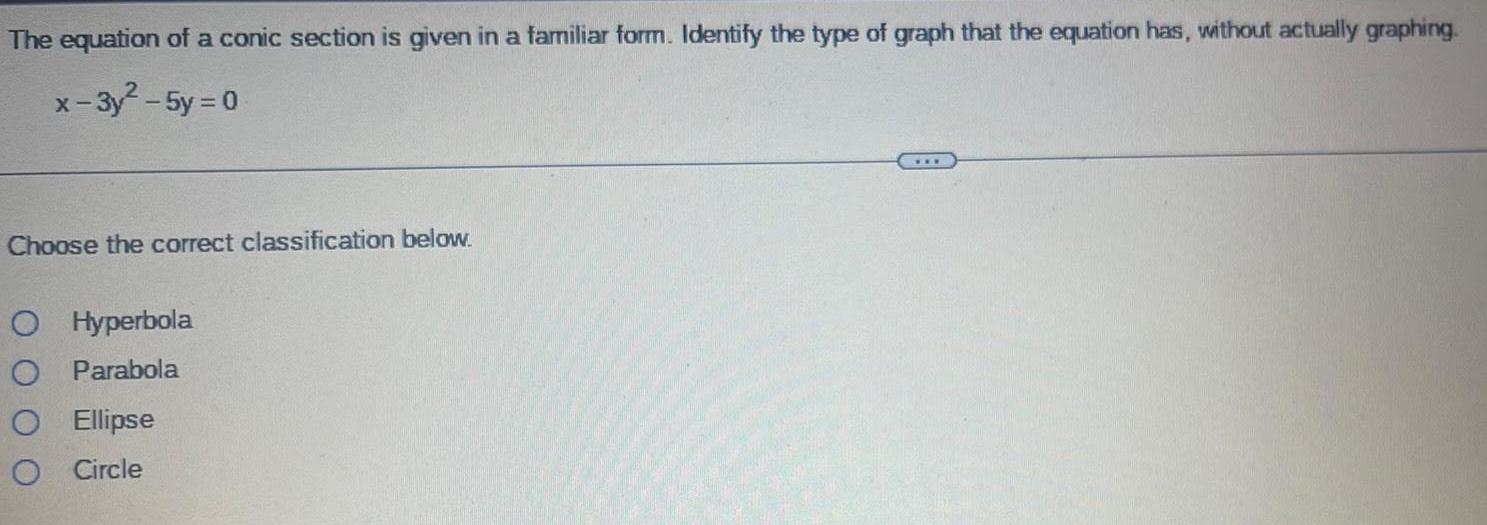
Math
FunctionsThe equation of a conic section is given in a familiar form. Identify the type of graph that the equation has, without actually graphing.
x-3y²-5y = 0
Choose the correct classification below.
Hyperbola
Parabola
Ellipse
Circle

Math
FunctionsA biologist observes a population of birds over a 10 year
period. At the beginning of the period, there were 223
thousand birds. By the end of the period, there were 182
thousand birds.
Assume the population of birds can be modeled using an
exponential function.
If P(t) is the population (in thousands), where t is the
time since the start of the period, then P(t)
___________(Round your parameters to four decimal places)
The population of birds reached 149 thousand ___________
after the start of the observation period (Round your answer to the nearest
whole number)
What will the population of birds be 17 years after the start of the observation period? ___________
(Round your answer to the nearest thousand)
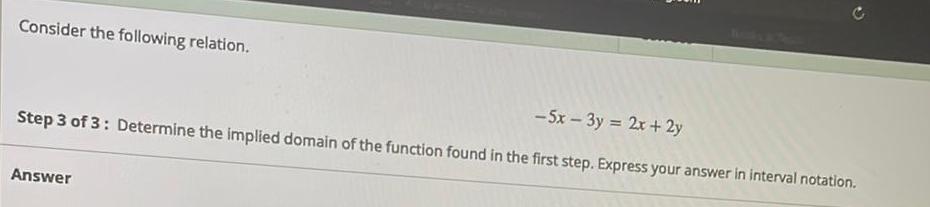
Math
FunctionsConsider the following relation.
-5x-3y = 2x + 2y
Step 3 of 3: Determine the implied domain of the function found in the first step. Express your answer in interval notation.
Answer

Math
FunctionsWhat is the range of the secant function?
A) all real numbers greater than or equal to 1 or less than or equal to -1
B) all real numbers, except odd multiples of π/2(90)⁰
C) all real numbers
D) all real numbers from-1 to 1, inclusive
Math
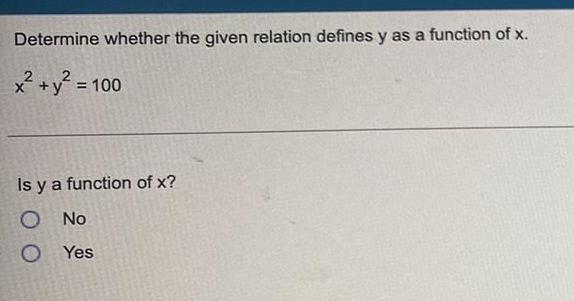
FunctionsDetermine whether the given relation defines y as a function of x.
x² + y² = 100
Is y a function of x?
No
Yes

Math
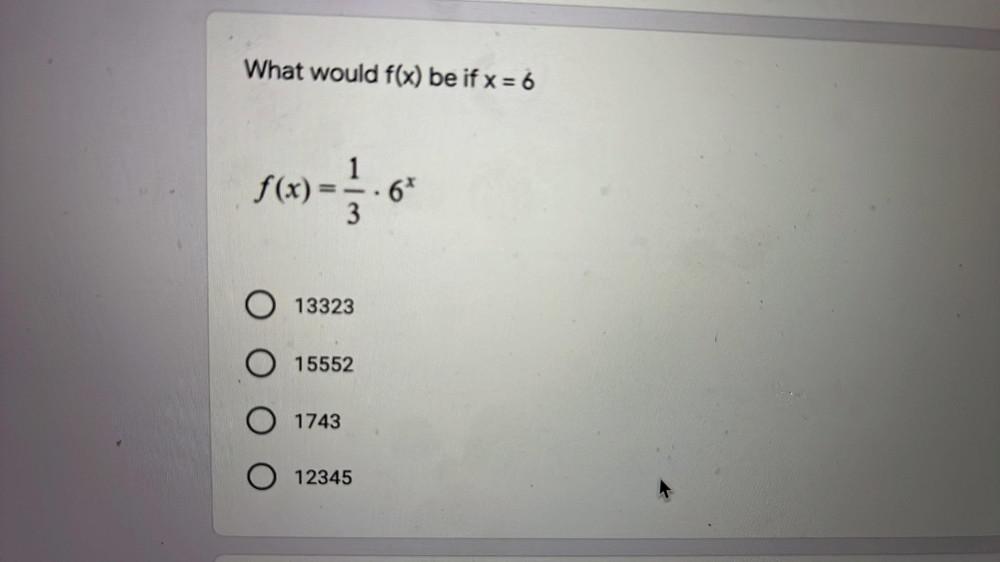
FunctionsFind the first-order Fourier approximation to f(t)=t+5. That is, find the the best approximation to f(t) by functions in Span{1,cos(t),sin(t)}
Math
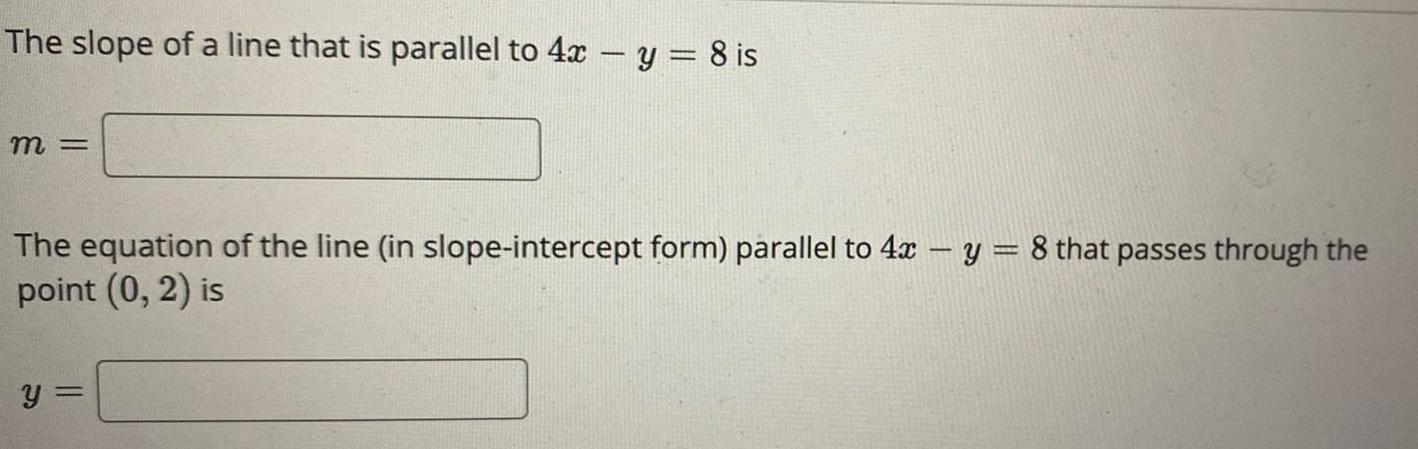
FunctionsThe slope of a line that is parallel to 4x-y=8 is
m = ________
The equation of the line (in slope-intercept form) parallel to 4x-y=8 that passes through the point (0, 2) is
y= __________

Math
FunctionsLet f be the one-to-one function given below. f(x)=(5x-4)/(6x-3)
(a) Find the inverse function of f (i.e., f-¹(x).)
f-¹(x) = _____
(b) Compute f-¹(-1).
f-¹(-1)=_____
Math
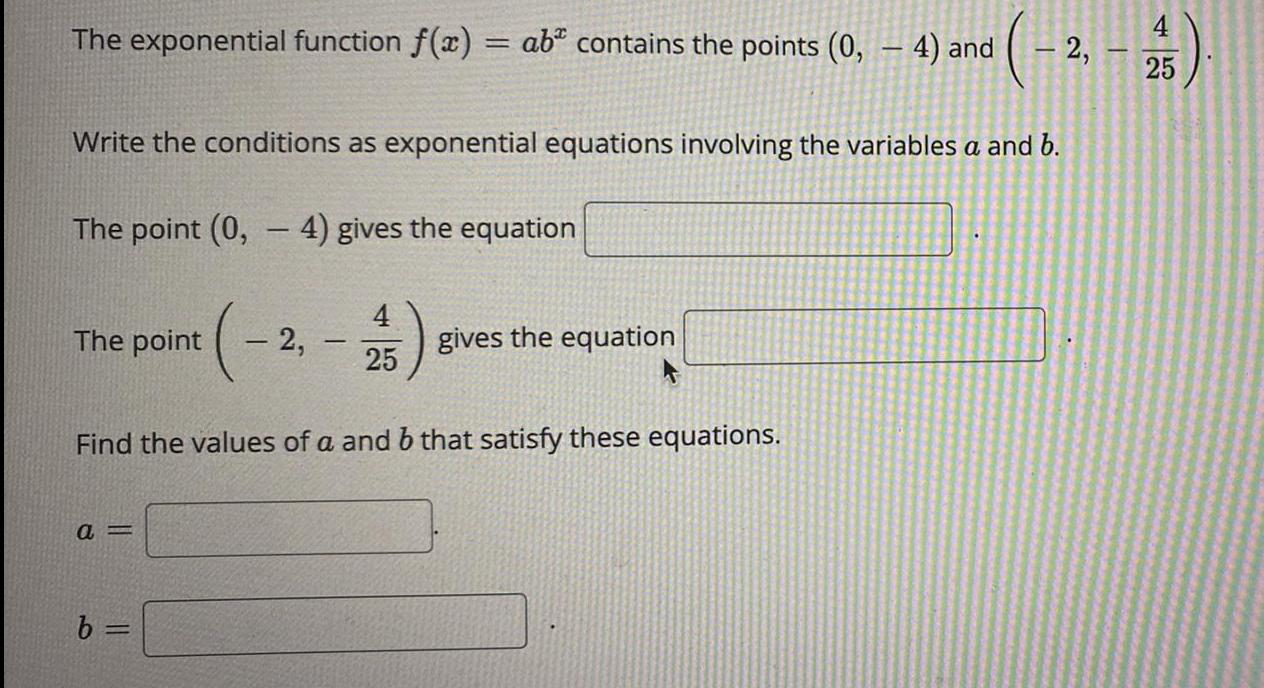
FunctionsThe exponential function f(x)=ab^x contains the points (0, - 4) and (-2, -4/25). Write the conditions as exponential equations involving the variables a and b.
The point (0, -4) gives the equation ________.
The point (-2, -4/25) gives the equation ________.
Find the values of a and b that satisfy these equations.
a= _________.
b= _________.