Functions Questions and Answers
Math
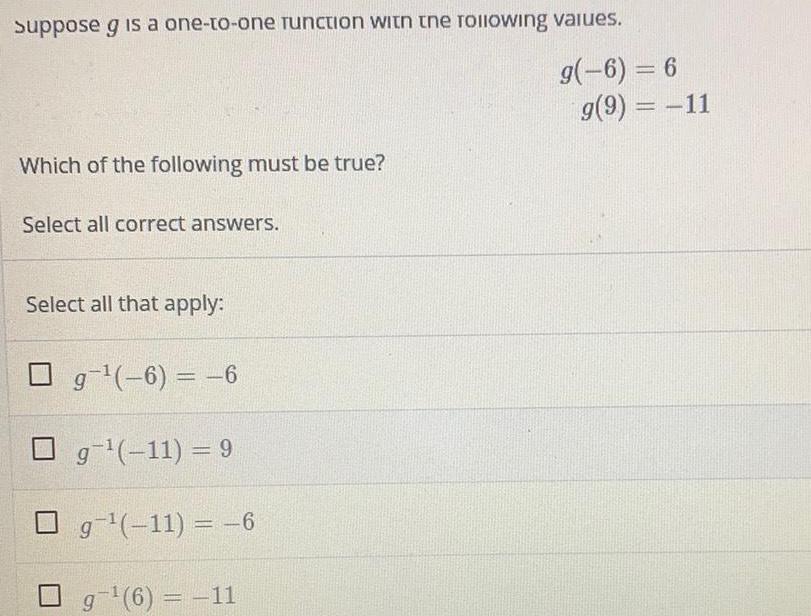
Functionssuppose g is a one-to-one Tunction with the following values.
g(-6) = 6
Which of the following must be true?
Select all correct answers.
Select all that apply:
g¹(-6) = -6
g ¹(-11) = 9
g ¹(-11) = -6
g-¹ (6) = -11
g(9) = -11

Math
FunctionsFind the domain and the range of the function. (Enter your answers using interval notation.)
h(x)= = -√x+2

Math
FunctionsDetermine whether the graph of the equation is symmetric with respect to the y-axis, the x-axis, the origin, more than one of these, or none of these.
x=y² + 14
Select all that apply.
x-axis
y-axis
origin
none of these
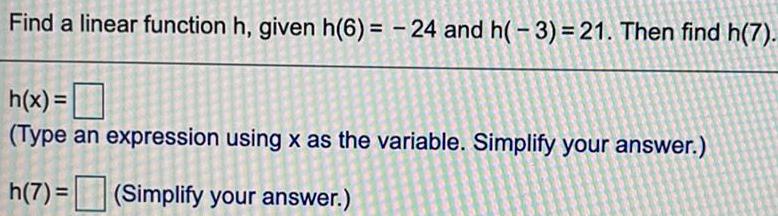
Math
FunctionsFind a linear function h, given h(6)= -24 and h(-3)=21. Then find h(7).
h(x) =
(Type an expression using x as the variable. Simplify your answer.)
h(7)= (Simplify your answer.)

Math
FunctionsSketch the graphs of the three functions by hand on the same rectangular coordinate system. Verify your results with a graphing utility.
f(x) = x²
g(x) = 1/5x^2 +3
h(x) = -1/5x^2

Math
FunctionsThe one-to-one function h is defined below
h(x) = 4x-5 / 7x+1
Find h⁻¹(x), where h⁻¹ is the inverse of h.
Also state the domain and range of h⁻¹ in interval notation.

Math
FunctionsGiven the graph of y = f(x), shown as a red dashed curve, drag the green movable points to draw the graph of
y = -f(x).
Notice that you can control the positioning of the reflective function with the coordinate labeled "Drag Function" and control
the width of the reflection with the coordinate labeled "Control Width."
![Let f(x) = x⁴ - x³ - 2x².
Identify the graph of f (x). [Hint: Use the zeros, the local behavior, and the end behavior to help you graph the function.]](https://media.kunduz.com/media/sug-question/raw/84433544-1657993400.4523091.jpeg?w=256)
Math
FunctionsLet f(x) = x⁴ - x³ - 2x².
Identify the graph of f (x). [Hint: Use the zeros, the local behavior, and the end behavior to help you graph the function.]

Math
FunctionsThe one-to-one function f is defined below.
f(x) = -3x / x - 7
Find f⁻¹(x), where f⁻¹ is the inverse of f.
Also state the domain and range of f⁻¹ in interval notation.

Math
FunctionsThe one-to-one function h is defined below.
h (x) = 9x-8 / 7x +9
Find h⁻¹(x), where h⁻¹ is the inverse of h.
Also state the domain and range of h⁻¹ in interval notation.
Math
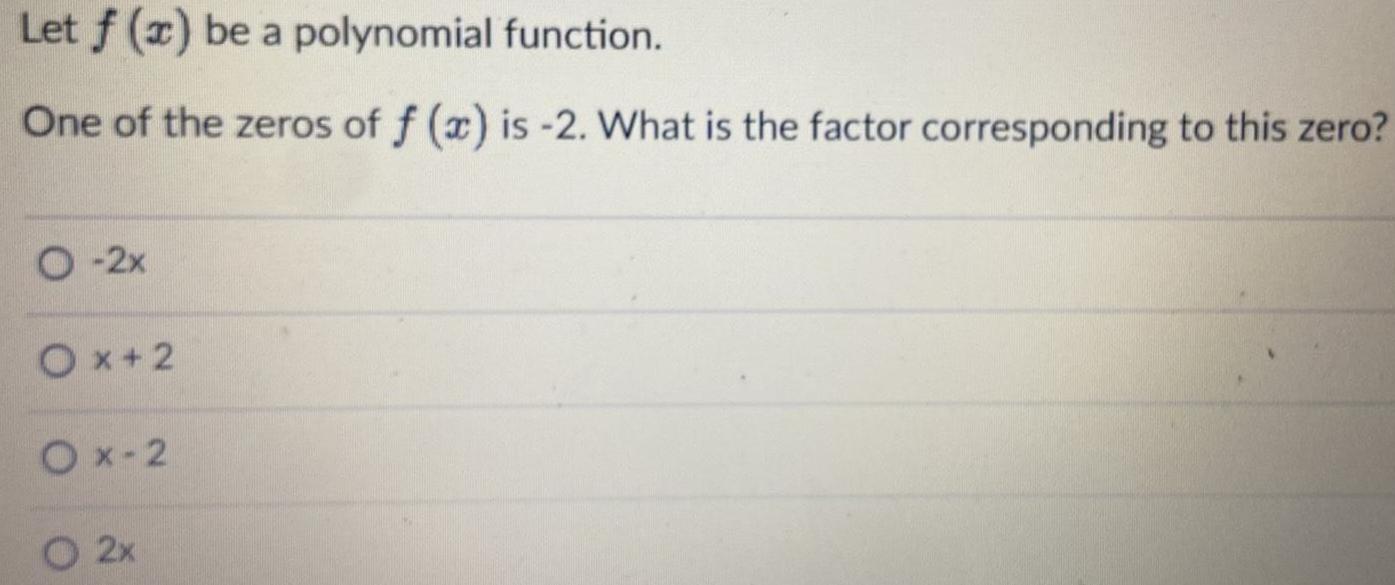
FunctionsLet f(x) be a polynomial function.
One of the zeros of f (x) is -2. What is the factor corresponding to this zero?
-2x
x + 2
x - 2
2x

Math
FunctionsLet f (x) be a polynomial function.
If one of the zeros of f (x) is -3i, what is another zero of f (x)?
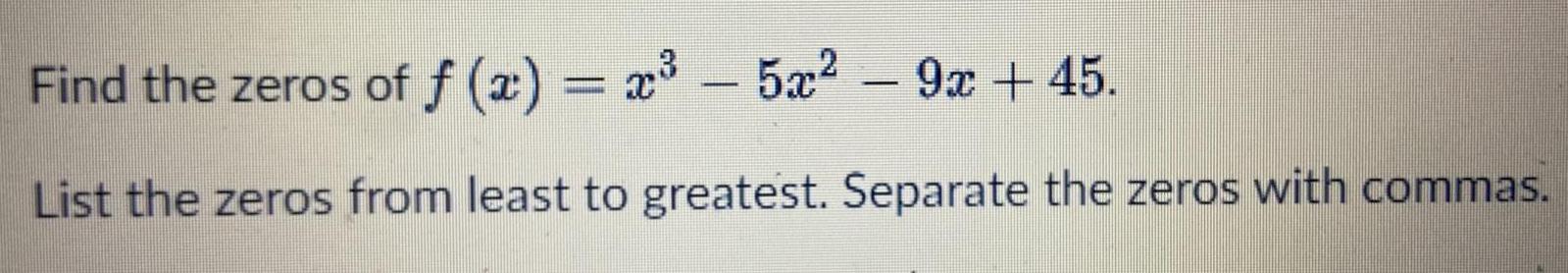
Math
FunctionsFind the zeros of f(x) = x³ - 5x² - 9x + 45.
List the zeros from least to greatest. Separate the zeros with commas.
Math
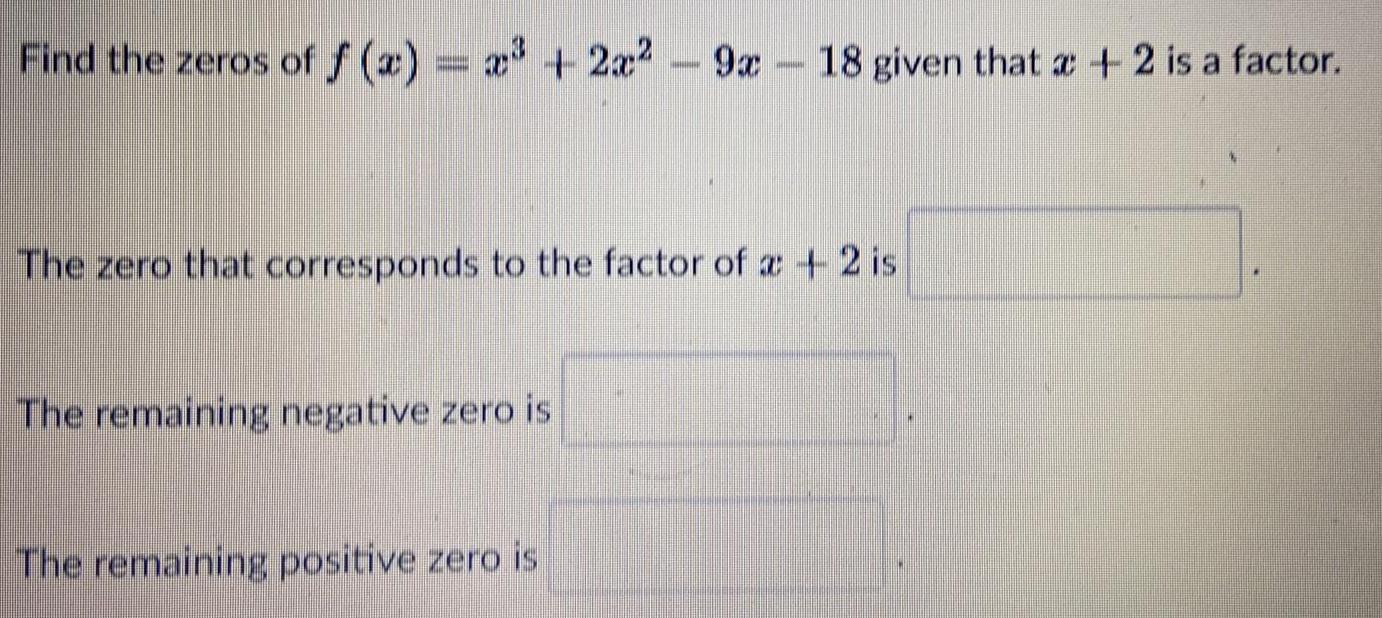
FunctionsFind the zeros of f(x) = x³ + 2x² -9x - 18 given that x + 2 is a factor.
The zero that corresponds to the factor of x+ 2 is
The remaining negative zero is
The remaining positive zero is

Math
FunctionsFind a degree 4 polynomial with real coefficients that has zeros of -1, 3, 2i, such that f(2)= 48.
f(x)=-2 (x +1) (x − 3)(x² + 4)
f(x) = (x + 1)(x - 3) (x² + 4)
f(x) = 1/2(x + 1)(x - 3) (x² + 4)
Of(z) = 2 (x +1) (x − 3)(x² + 4)
Math
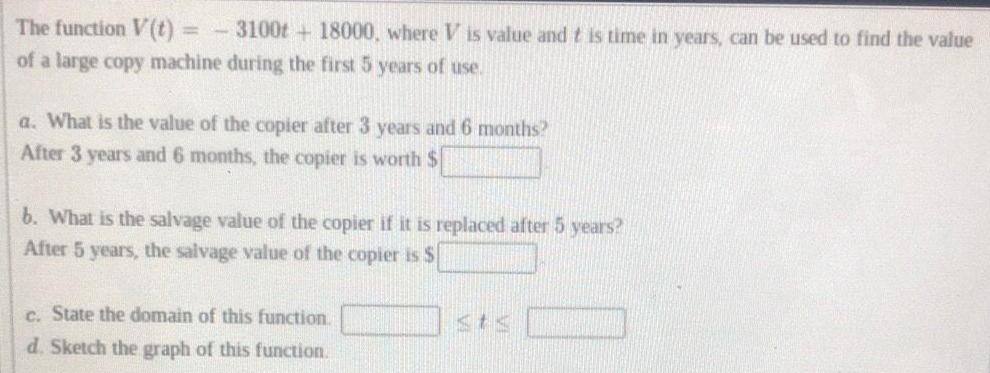
FunctionsThe function V(t) = - 3100+ 18000, where V is value and t is time in years, can be used to find the value of a large copy machine during the first 5 years of use.
a. What is the value of the copier after 3 years and 6 months?
After 3 years and 6 months, the copier is worth $
b. What is the salvage value of the copier if it is replaced after 5 years?
After 5 years, the salvage value of the copier is S
c. State the domain of this function.
d. Sketch the graph of this function.

Math
FunctionsThe one-to-one function f is defined below.
f(x) =7x / 7-3x
Find f¹(x), where f⁻¹ is the inverse of f.
Also state the domain and range of f⁻¹ in interval notation.

Math
FunctionsA ball is thrown straight up, from 3m above the ground, with a velocity of 14 m/s. It
can be modeled by the function below. When will the ball hit the ground?
h(t) = −5ť² + 14t + 3
t = 11.4
t=3
t = 14.2
t = 0.2
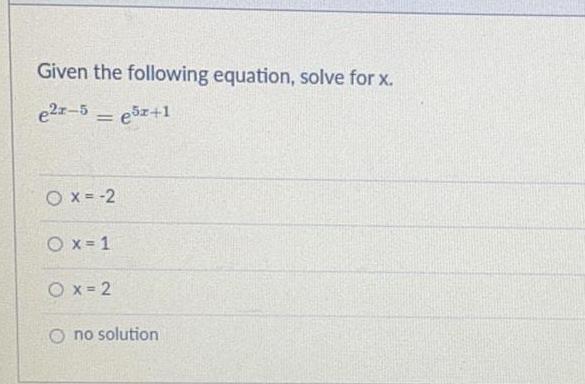

Math
FunctionsSelecting an option will display any text boxes needed to complete your answer.
No Solution (Ø)
One Solution
Two Solutions

Math
Functionsg(x) = cax is a way of symbolizing any exponential function. Choose
specific numbers for c and a and make a table that contains ordered pairs,
(x, y), that fit your exponential function, for x = -2, -1, 0, 1, 2, 3.
Math
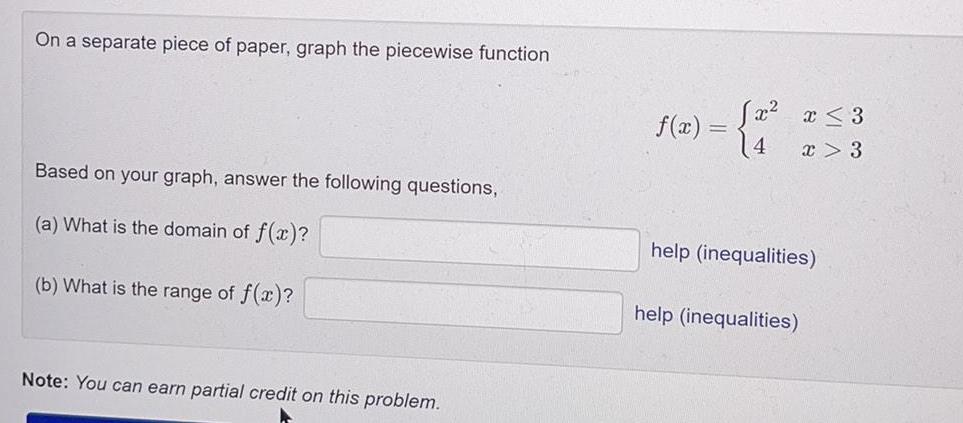
FunctionsOn a separate piece of paper, graph the piecewise function
f(x) ={ x² x ≤ 3 }
4 x > 3
Based on your graph, answer the following questions,
(a) What is the domain of f(x)?
(b) What is the range of f(x)?
Note: You can earn partial credit on this problem.
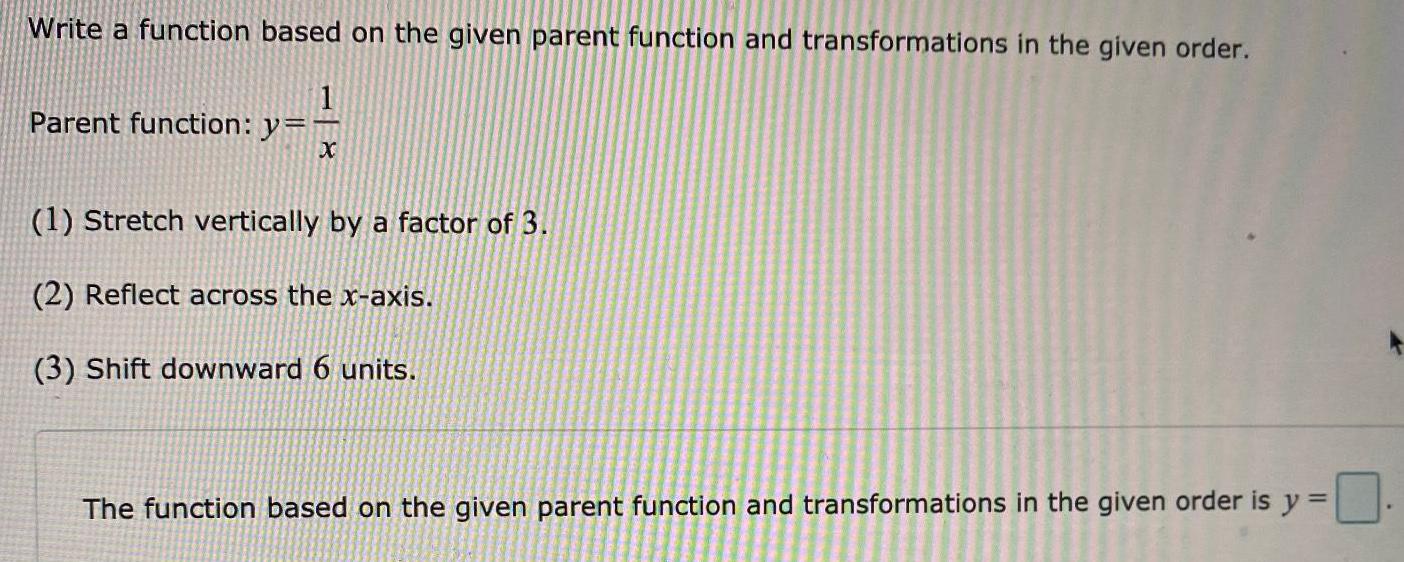
Math
FunctionsWrite a function based on the given parent function and transformations in the given order.
Parent function: y=1/x
(1) Stretch vertically by a factor of 3.
(2) Reflect across the x-axis.
(3) Shift downward 6 units.
The function based on the given parent function and transformations in the given order is y=

Math
FunctionsIf f(x)=1-5x, find each of the following.
(a) f(-6) (b) f(0) (c) f(9)
(a) f(-6)
(Simplify your answer.)
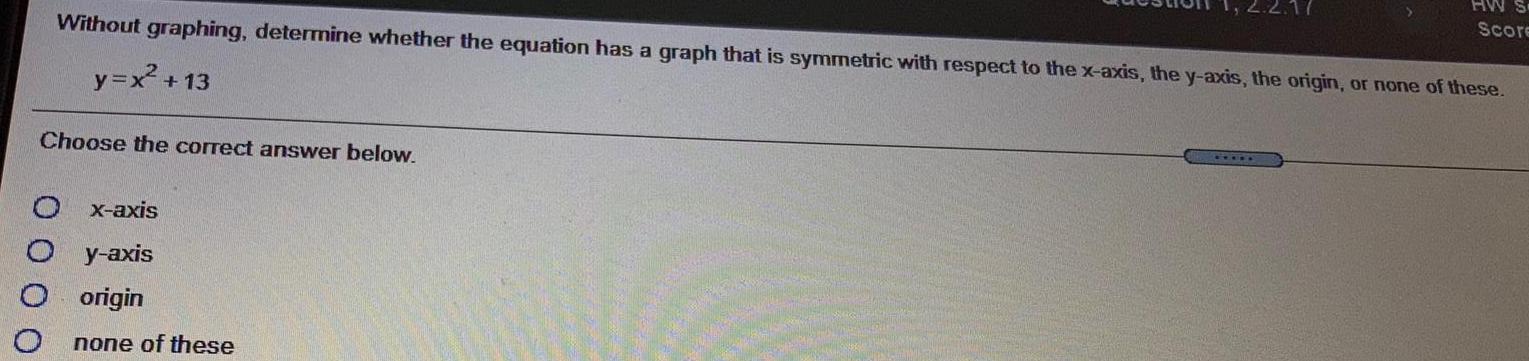
Math
FunctionsWithout graphing, determine whether the equation has a graph that is symmetric with respect to the x-axis, the y-axis, the origin, or none of these.
y=x² +13
Choose the correct answer below.
x-axis
y-axis
origin
none of these

Math
FunctionsDetermine the domain and range of f-¹(a), given f(x) = 22x-1+3.
Domain: (-∞, ∞) Range: (3, ∞)
Domain: (1, ∞) Range: (3, ∞)
Domain: (3, ∞) Range: (-∞,∞)
Domain: (1/2,∞) Range: (-∞, ∞)
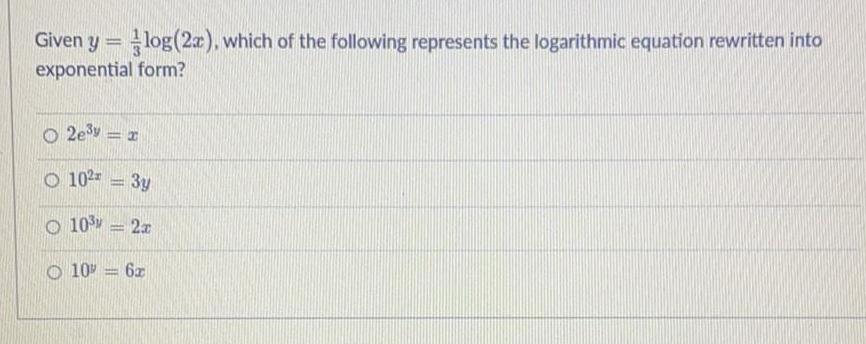
Math
FunctionsGiven y = 1/3log(2x), which of the following represents the logarithmic equation rewritten into
exponential form?
2e³y=x
10²=3y
10³ = 2x
10 = 6x

Math
FunctionsConsider the quadratic function f(x) = -2x² + 4x + 2. Find the y-intercept and the equation of the axis of symmetry.
The y-intercept is 2.
The equation of the axis of symmetry is x = 1.
The y-intercept is -2.
The equation of the axis of symmetry is x = -1.
The y-intercept is -1.
The equation of the axis of symmetry is x = -2.
The y-intercept is 1.
The equation of the axis of symmetry is x = 2.

Math
FunctionsDescribe how to transform the graph of y=e* on to the graph y=-e^x-¹ +4.
The graph has a vertical shift up 4 units, a reflection over the x axis and a horizontal shift to the left 1 unit.
The graph has a vertical shift up 4 units, a reflection over the x axis and a horizontal shift to the right 1 unit.
The graph has a vertical shift down 4 units, a reflection over the x axis and a horizontal shift left 1 unit. The graph has a vertical shift down 4 units, a reflection over the y axis and a horizontal shift right one unit.

Math
Functionsf(-2) =
f(-1) =
Using the function f(x) given above, find the
following function values:
f(0) =
f(1) =
f(2)=
[3-x²,
f(3) =
x < -1
2.x. 1<x<3
x 23
5-x,
If the answer is no solution, write "no
solution".
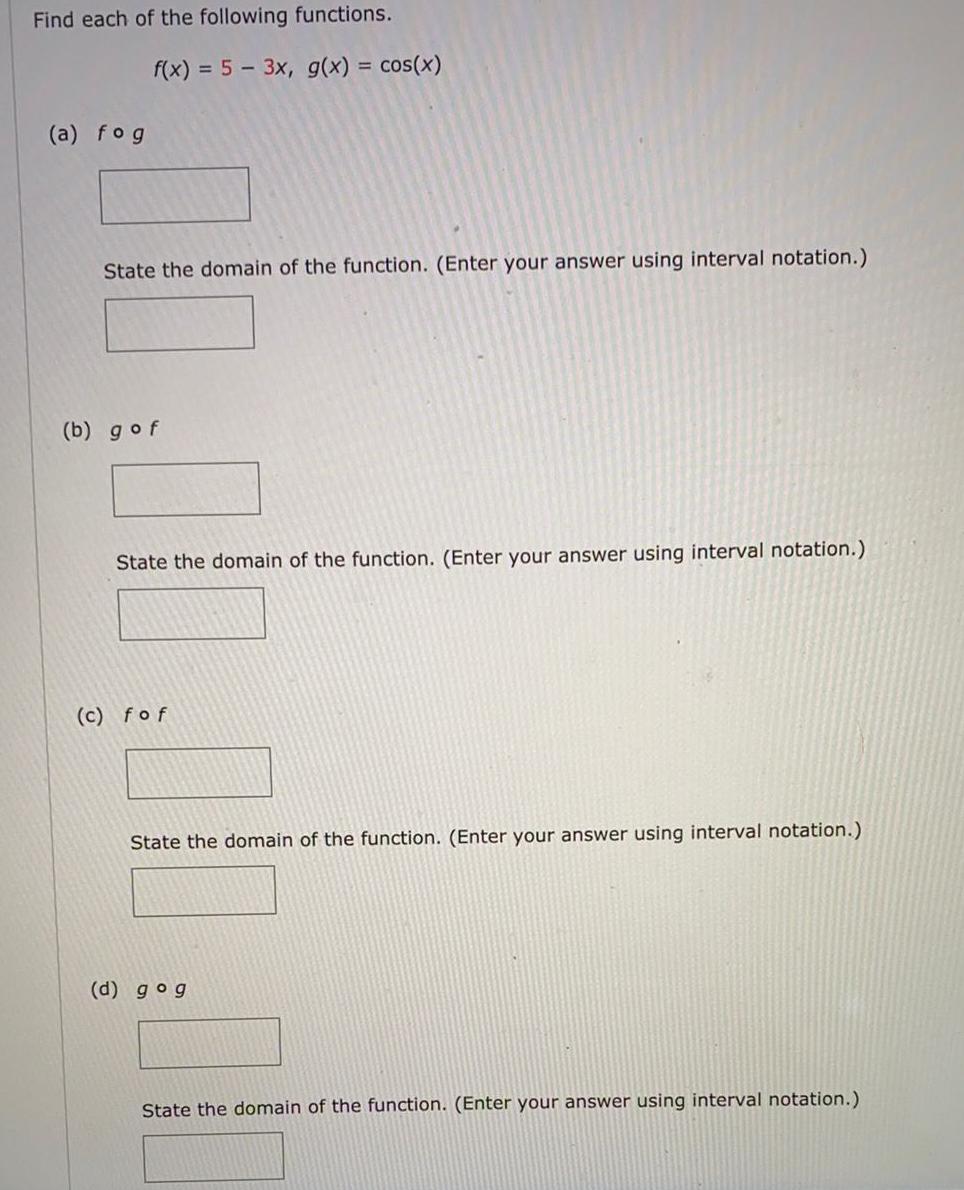
Math
FunctionsFind each of the following functions.
(a) fog
f(x) = 5-3x, g(x) = cos(x)
State the domain of the function. (Enter your answer using interval notation.)
(b) gof
State the domain of the function. (Enter your answer using interval notation.)
(c) fof
State the domain of the function. (Enter your answer using interval notation.)
(d) gog
State the domain of the function. (Enter your answer using interval notation.)

Math
FunctionsEvaluate the function f(x)=x² + 7x + 1 at the given values of the independent variable and simplify.
a. f(-7) b. f(x + 2)
c. f(-x)
a. f(-7)= (Simplify your answer.)

Math
FunctionsGiven the function f(x) = x³-2 and g(x) = 1/2x³+3, which describes the transformations
applied to the function f(x) so it falls onto g(x)?
The graph of g(x) has a vertical stretch by a factor of 1/2 and a vertical shift up 3 from the function of f(x).
The graph of g(x) has a vertical shrink by a factor of 1/2 and a vertical shift up 5 from the function of f(x).
The graph of g(x) has a vertical stretch by a factor of 1/2 and a vertical shift up 5 from the function of f(x).
The graph of g(x) has a vertical shrink by a factor of 1/2 and a vertical shift up 3 from the function of f(x).
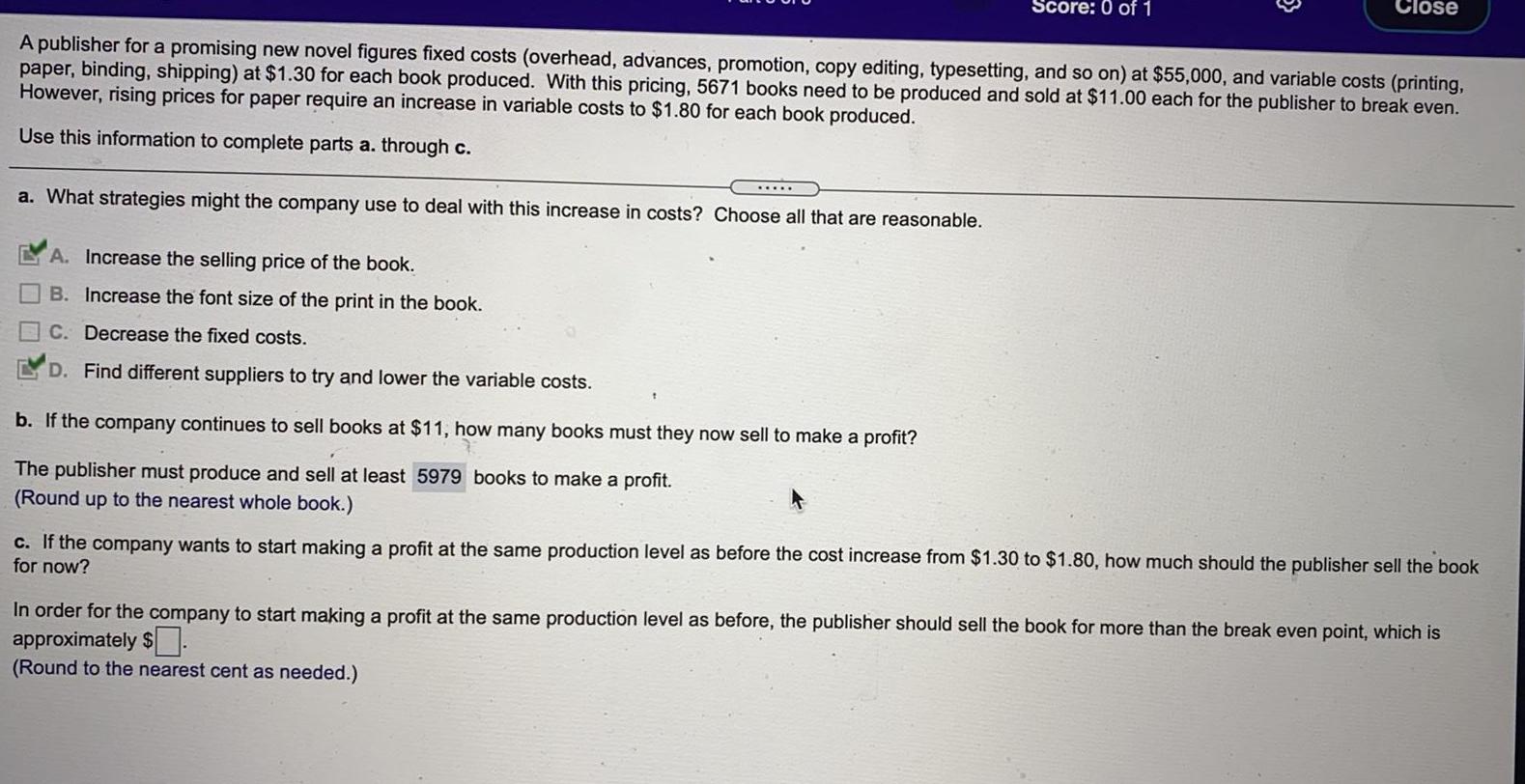
Math
Functionsa. What strategies might the company use to deal with this increase in costs? Choose all that are reasonable.
A publisher for a promising new novel figures fixed costs (overhead, advances, promotion, copy editing, typesetting, and so on) at $55,000, and variable costs (printing,
paper, binding, shipping) at $1.30 for each book produced. With this pricing, 5671 books need to be produced and sold at $11.00 each for the publisher to break even.
However, rising prices for paper require an increase in variable costs to $1.80 for each book produced.
Use this information to complete parts a. through c.
A. Increase the selling price of the book.
B. Increase the font size of the print in the book.
C. Decrease the fixed costs.
D. Find different suppliers to try and lower the variable costs.
Score: 0 of 1
b. If the company continues to sell books at $11, how many books must they now sell to make a profit?
The publisher must produce and sell at least 5979 books to make a profit.
(Round up to the nearest whole book.)
Close
c. If the company wants to start making a profit at the same production level as before the cost increase from $1.30 to $1.80, how much should the publisher sell the book
for now?
In order for the company to start making a profit at the same production level as before, the publisher should sell the book for more than the break even point, which is
approximately $
(Round to the nearest cent as needed.)

Math
FunctionsUse a graphing utility to approximate (to two decimal places) any relative minima or maxima
of the function. (If an answer does not exist, enter DNE.) *
f(x) = x (x + 3)

Math
FunctionsA house was valued at $100,000 in the year 1995. The value appreciated to $150,000 by the year 2000.
A) If the value is growing exponentially, what was the annual growth rate between 1995 and 2000?
Round the growth rate to 4 decimal places.
B) What is the correct answer to part A written in percentage form?
C) Assume that the house value continues to grow by the same percentage. What will the value equal in the
year 2003 ?
Round to the nearest thousand dollars.

Math
FunctionsExpress the function h(z) =-2 .3^2x in the form h(x) = (ƒ o g)(z) where ƒ(x) ≠x and g(x) ≠x
a) g(x) =
b) f(x) =
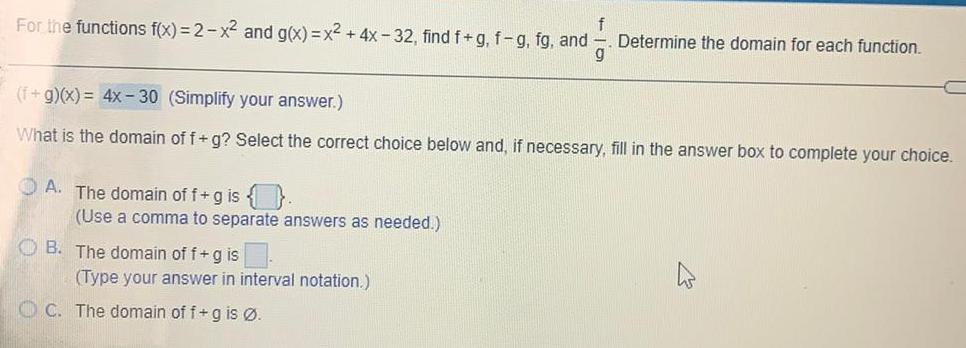
Math
FunctionsFor the functions f(x)=2-x² and g(x)=x² + 4x-32, find f+g, f-g, fg, and f/g
(f+g)(x) = 4x - 30 (Simplify your answer.)
What is the domain of f+g? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The domain off+g is {}.
(Use a comma to separate answers as needed.)
B. The domain of f + g is.
(Type your answer in interval notation.)
Determine the domain for each function.
C. The domain of f+g is Ø.
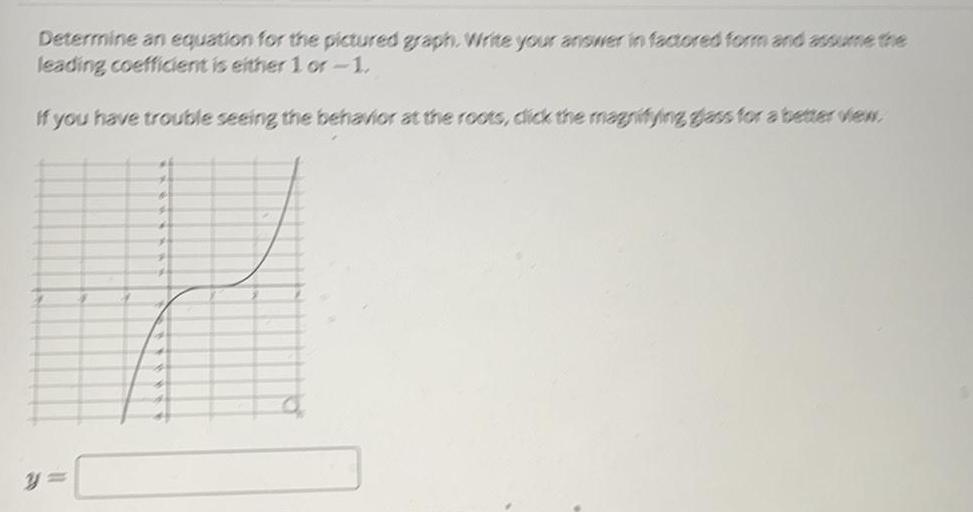
Math
FunctionsDetermine an equation for the pictured graph. Write your answer in factored form and assume the
leading coefficient is either 1 or -1.
If you have trouble seeing the behavior at the roots, click the magnifying glass for a better view.

Math
FunctionsConstruct a polynomial function with the stated properties. Reduce all fractions to lowest terms.
Third-degree, with zeros of -2,-1, and 3, and passes through the point (2, 9).
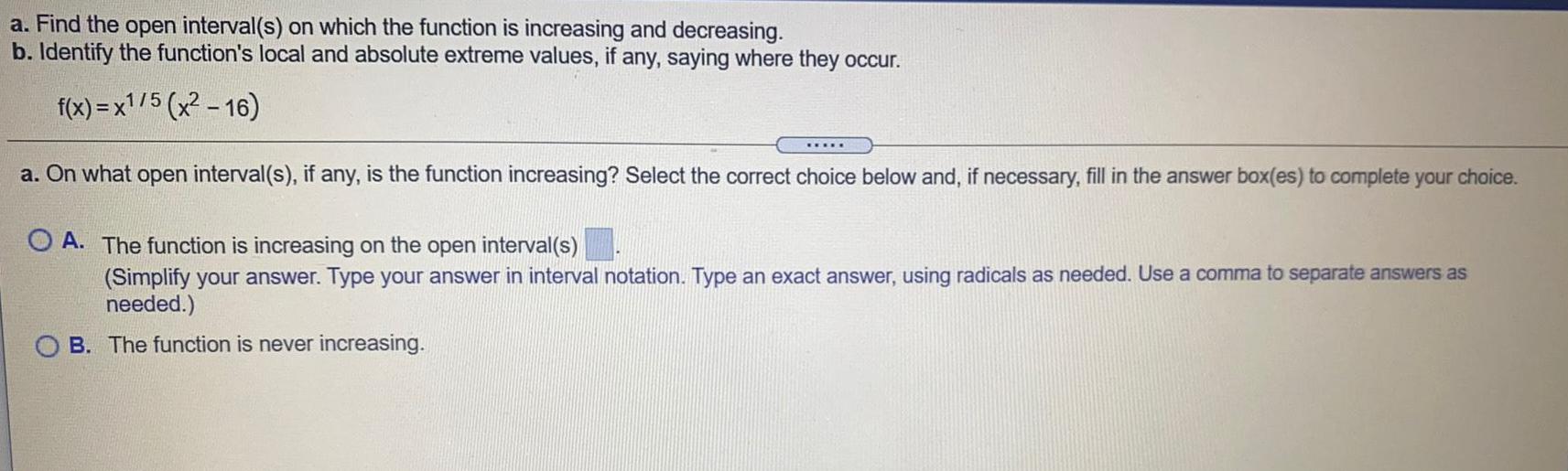
Math
Functionsa. Find the open interval(s) on which the function is increasing and decreasing.
b. Identify the function's local and absolute extreme values, if any, saying where they occur.
f(x)=x1/5 (x²-16)
a. On what open interval(s), if any, is the function increasing? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
A. The function is increasing on the open interval(s)
(Simplify your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed. Use a comma to separate answers as
needed.)
B. The function is never increasing.

Math
FunctionsThere's a roughly linear relationship between the length of someone's femur
(the long leg-bone in your thigh) and their expected height. Within a certain
population, this relationship can be expressed using the formula
h = 2.38f +57.7, where h represents the expected height in centimeters
and f represents the length of the femur in centimeters. What is the meaning
of the h-value when f = 54?
The expected height for someone with a femur length of 186.22
centimeters.
The expected height for someone with a femur length of
54 centimeters.
The change in expected height for every one additional centimeter of
femur length.
The femur length for someone with an expected height of 54
centimeters.

Math
FunctionsWhich of the following are True about the notation f(g(x)). Check all that apply.
g(x) is used as the input into f(x)
The output of one function is used as the input for another function
The process is called function composition.
f(x) is used as the input into g(x)

Math
FunctionsSuppose a homemade rocket is launched upward from a platform several feet above the ground with an initial upward
velocity of 76 feet per second.
Match each of the following prompts with the feature of the quadratic function you would need to find to respond to the
prompt:
ARAR
. Prompt
How long will it take for the rocket to hit the ground?
How long will it take for the rocket to reach its maximum height?
What is the maximum height of the rocket?
What is the initial height of the rocket?
Needed part of quadratic function
a. y-value of the vertex
b. x-value of the vertex or the axis of symmetry
c. positive x-intercept
d. y-intercept
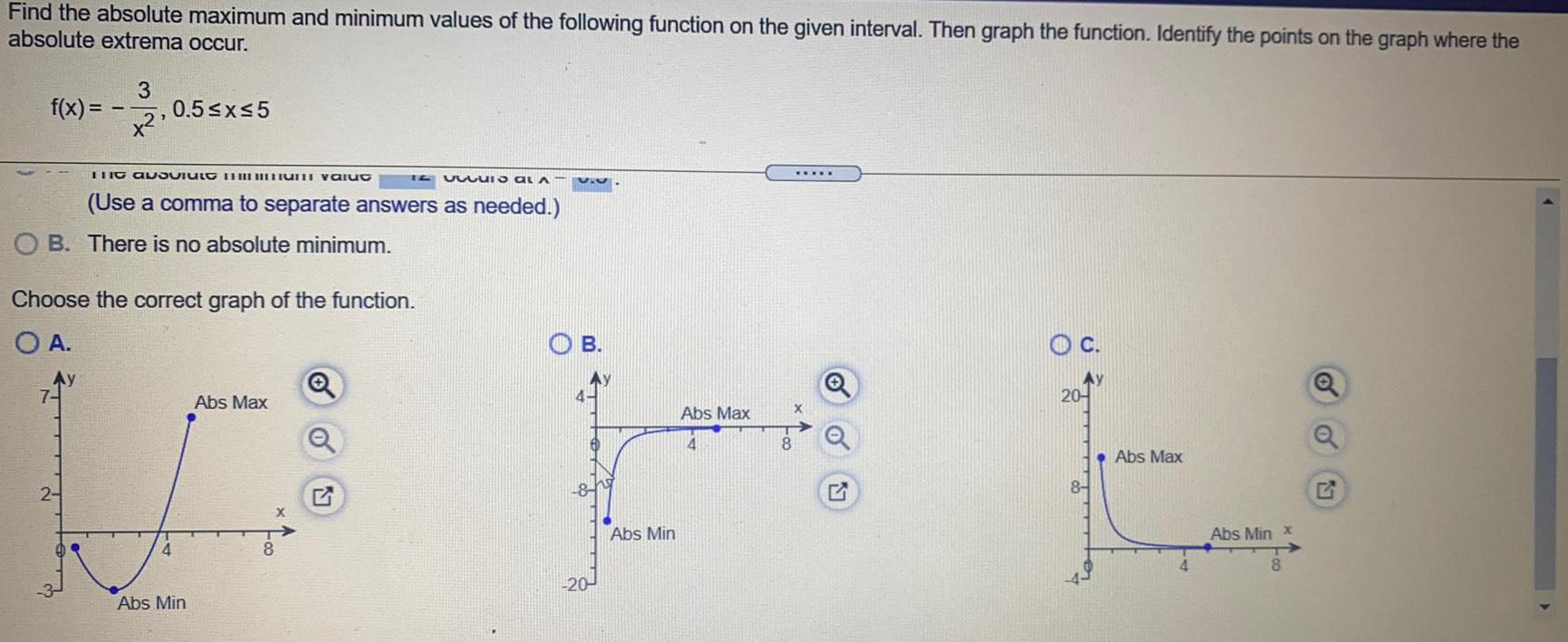
Math
FunctionsFind the absolute maximum and minimum values of the following function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur.
f(x) = -3/x2, 0.5≤x≤5
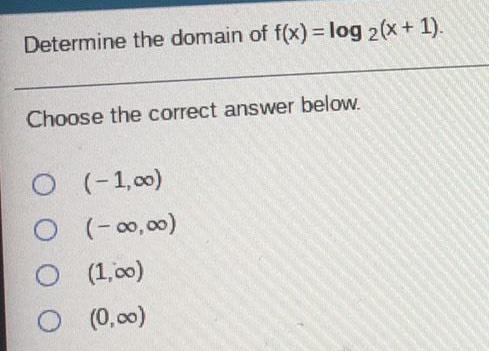
Math
FunctionsDetermine the domain of f(x) = log 2(x + 1). Choose the correct answer below.
(-1,00)
(-00,00)
(1,000)
(0,00)

Math
FunctionsMaya invested her savings in two investment funds. The $3000 that she invested in Fund A returned a 10% profit. The amount that she invested in Fund B
returned a 3% profit. How much did she invest in Fund B, if both funds together returned a 6% profit?
Amount invested in Fund B: $
X
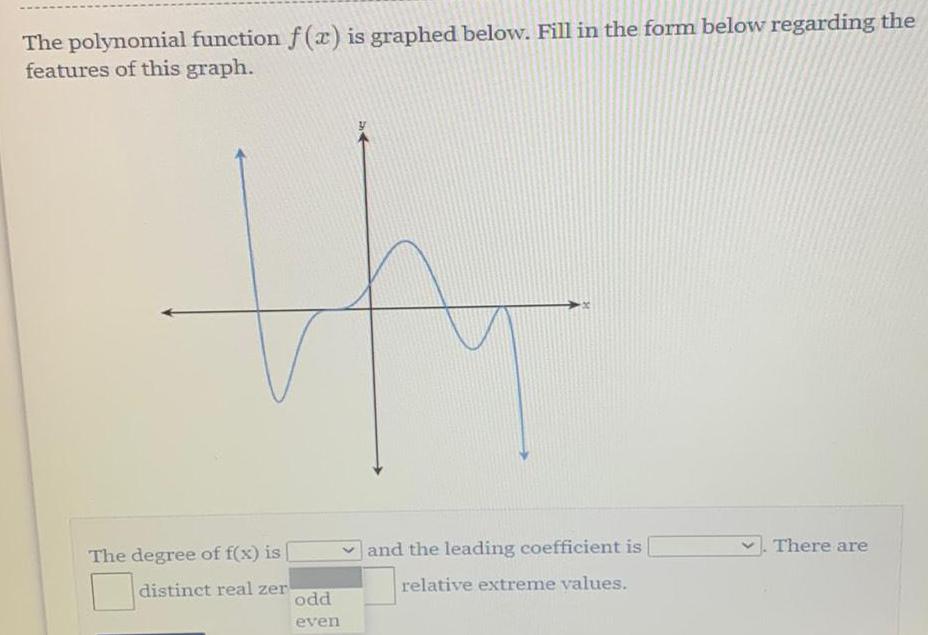
Math
FunctionsThe polynomial function f(x) is graphed below. Fill in the form below regarding the
features of this graph.
The degree of f(x) is [
distinct real zer
odd
even
and the leading coefficient is relative extreme values. There are

Math
FunctionsApproximate each number using a calculator.
(a) 173.14
(b) 173.141
(a) 173.14
(c) 173.1415
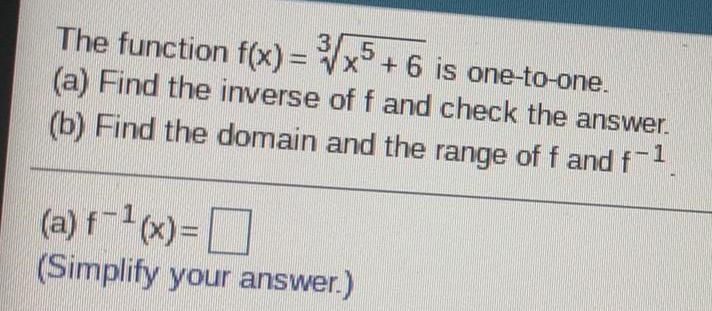
Math
FunctionsThe function f(x)=3√x^5 + 6 is one-to-one.
(a) Find the inverse of f and check the answer.
(b) Find the domain and the range of f and f-1
(a) f-¹(x)=
(Simplify your answer.)