Functions Questions and Answers

Math
FunctionsLet f(x) = x² - 4x - 21 and g(x) = x² − 9x + 14. Find f.g and f/g respective domains. Simplify your answers.
1. f. g =
2. What is the domain of f. g ?
Answer (in interval notation):
3. f/g =
Answer (in interval notation):
4. What is the domain of f/g?
Answer (in interval notation):

Math
FunctionsWrite a rule for g described by the transformations the vertex. of the graph off. Then identify 2 f(x) = x²; vertical stretch by a factor of 4 and a reflection in the x-axis, followed by a translation 1 unit left.
a. g(x) = -4(x + 1)²; (-1,0)
b. g(x) = 4x² + 1; (0,1)
c. g(x)=-1/4 (x + 1)² ; (-1,0)
d. g(x) = 4(x + 1)²; (-1,0)

Math
Functionsf(x) = (2x - 1)(3x + 5) (x + 1) has zeros at x = -5/3, x=-1 and x=1/2
What is the sign of f on the interval -5/3<x<1/2?
Choose 1 answer:
f is always positive on the interval.
f is always negative on the interval.
f is sometimes positive and sometimes negative on the interval.

Math
FunctionsGraph y = 5(2)^(x-1)-8
by clicking the icon below and then there are two main steps:
1st, click where the horizontal asympotote will be.
2nd, click two points on the graph to create the graph itself.


Math
FunctionsThe domain of function r is (-∞, -7) U (-7, 5) U (5, ∞), and the value of the function approaches 1 as x approaches -∞ and ∞. Which function could be function r?
A. f(x) = x-5/x+7
B. f(x) = 2x-35/x^2+2x-35
C. f(x) = x^2-3x-15/x^2+2x-35
D. f(x) = x^2+2x-35/x^2-3x-15

Math
FunctionsUse the graph to determine the following.
a. the function's domain
b. the function's range
c. the x-intercepts, if any
d. the y-intercept, if any
e. the function value indicated below.

Math
FunctionsEvaluate the function h(x)=x^4-2x²-5 at the given values of the independent variable and simplify.
a. h(3)
b.h(-1)
c. h(-x)
d. h(3a)
Math
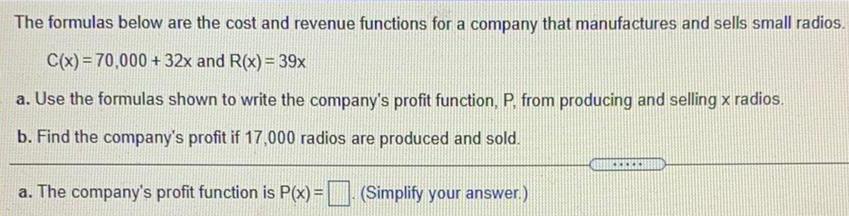
FunctionsThe formulas below are the cost and revenue functions for a company that manufactures and sells small radios.
C(x) = 70,000+32x and R(x) = 39x
a. Use the formulas shown to write the company's profit function, P. from producing and selling x radios.
b. Find the company's profit if 17,000 radios are produced and sold.
a. The company's profit function is P(x) =
(Simplify your answer.)

Math
FunctionsIf f(x) = log3(x), what is the transformation that occurs if g(x) = -log3(x)? (Enters for stretch, c for compress, mx for mirrorred across the x-axis, my for mirrored across the y-axis, r for shift right, I for shift left, u for shift up, and d for shift down.)

Math
FunctionsSelect all the correct answers.
A biologist models the size of a population of songbirds over time, t, in years, with this function.
f(t) 312(0.97)^t
Which statements about the population are supported by this function?
The population size was initially around 312.
The population size was initially around 303.
The population size when t=5 is predicted to be 361.
The population is increasing by 97% per year.
The population is decreasing by 3% per year.

Math
FunctionsIf y= alx-h| + k has the value of a = 1, the graph will be (assume h and k are greater than zero).
closer to the y-axis
translating the parent function hunits to the right and Kunits up
further from the Y-axis
reflecting across the X-axis

Math
FunctionsSketch the graph of the function and check the graph with a graphing calculator. Before doing so, describe how the graph of the function can be obtained from the graph of a basic exponential function.
f(x) = e2x
Describe how the graph of the function can be obtained from the graph of a basic exponential function.
Start with the graph of y=ex. Since the constant factor in the exponent is the graph should be
Math
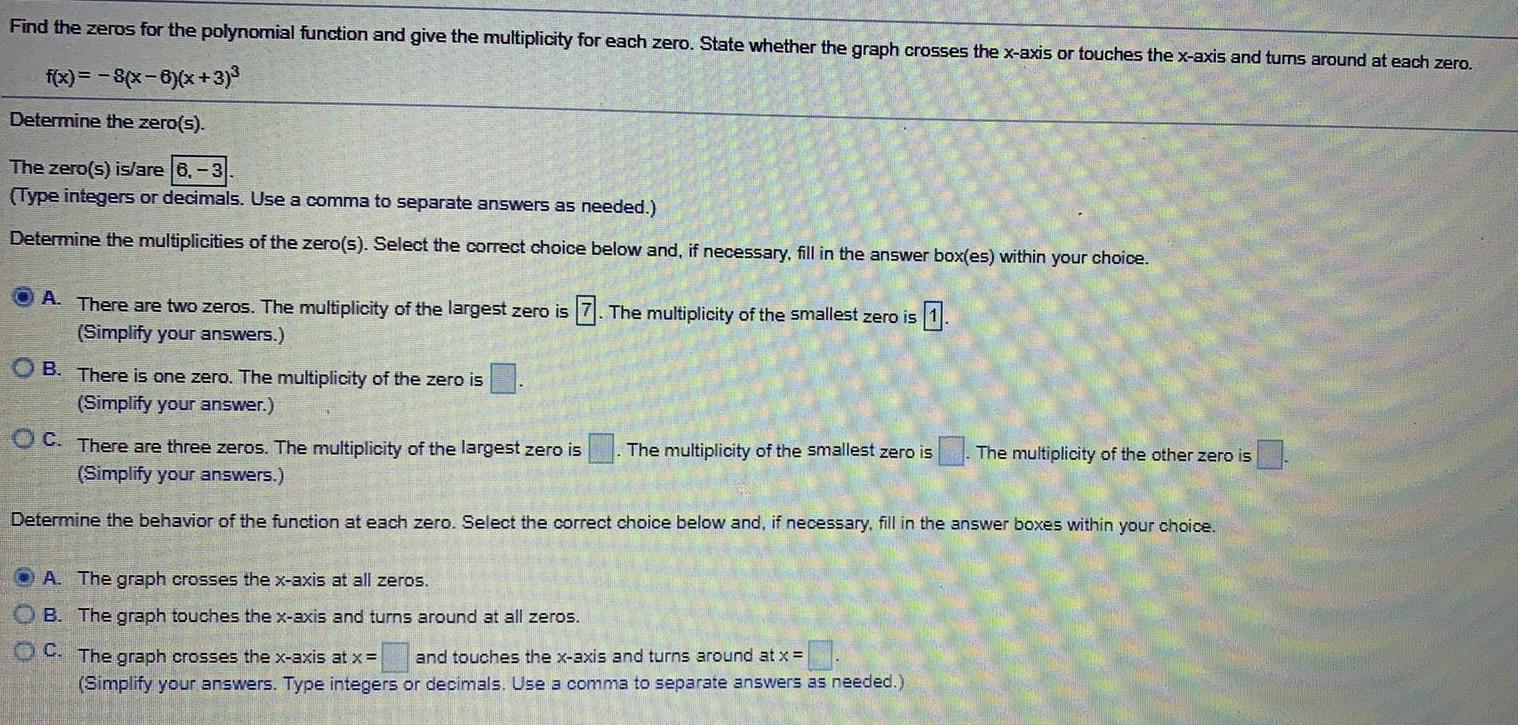
FunctionsFind the zeros for the polynomial function and give the multiplicity for each zero. State whether the graph crosses the x-axis or touches the x-axis and turns around at each zero.
f(x) = -8(x-6)(x+3)³
Determine the zero(s).
The zero(s) is/are
(Type integers or decimals. Use a comma to separate answers as needed.)
Determine the multiplicities of the zero(s). Select the correct choice below and, if necessary, fill in the answer box(es) within your choice.
A. There are two zeros. The multiplicity of the largest zero is. The multiplicity of the smallest zero is
(Simplify your answers.)
B. There is one zero. The multiplicity of the zero is
(Simplify your answer.)
C. There are three zeros. The multiplicity of the largest zero is The multiplicity of the other zero is
(Simplify your answers.)
Determine the behavior of the function at each zero. Select the correct choice below and, if necessary, fill in the answer boxes within your choice.
The multiplicity of the smallest zero is
A. The graph crosses the x-axis at all zeros.
B. The graph touches the x-axis and turns around at all zeros.
C. The graph crosses the x-axis at x = and touches the x-axis and turns around at x =
(Simplify your answers. Type integers or decimals. Use a comma to separate answers as needed.)

Math
FunctionsGiven the log function f(x) = 4 logx, state the coordinates of the image point if the original point was (10, 1). (ie. If (10, 1) is a point on the parent curve, what would be the coordinates of this point after applying transformations)?

Math
FunctionsFind the domain of the rational function.
f(x) 1 - 3x x²-10x+16
All real number except -8 and 2
All real numbers except 8, 2, 1 3, and 0
All real numbers except 8 and 2
All real numbers except 8, 2, and 1 3
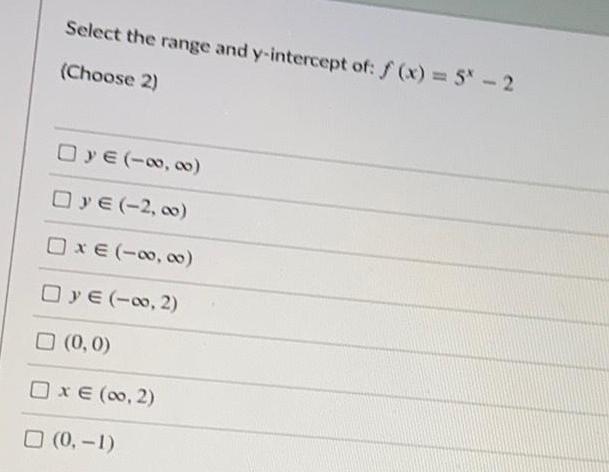
Math
FunctionsSelect the range and y-intercept of: f(x) = 5^x - 2
(Choose 2)
y ∈ (-∞, ∞)
y ∈ (-2,∞)
x ∈ (-∞,∞)
y ∈ (-∞, 2)
(0,0)
x ∈ (0, 2)
(0,-1)

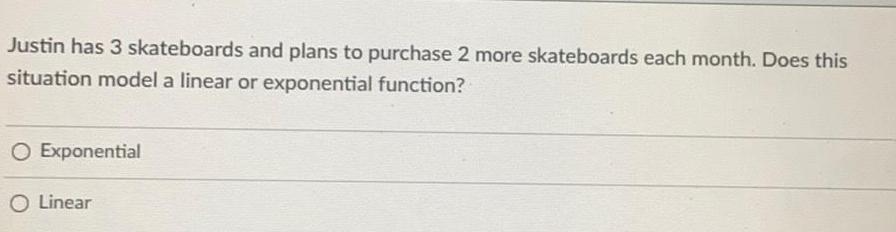
Math
FunctionsJustin has 3 skateboards and plans to purchase 2 more skateboards each month. Does this situation model a linear or exponential function?
Exponential
Linear

Math
FunctionsPart A
Would kind of line would you use to graph the linear inequality: y ≤2x-4
Part B
Where would you shade the solutions to the linear inequality: y ≤ 2x - 4
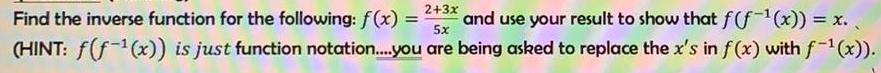
Math
FunctionsFind the inverse function for the following: f(x) =2+3x /5x and use your result to show that f(f-¹(x)) = x.
(HINT: f(f-¹(x)) is just function notation....you are being asked to replace the x's in f(x) with f-¹(x)).
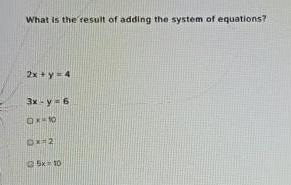

Math
FunctionsTo demonstrate your understanding of the "mathematical language" used in this course, give an
example of each of the following.
(a) a square root function that has been vertically stretched by a factor of 4, reflected in the y-axis, horizontally stretched by a factor of 2, and translated 3 units left and 5 units up.
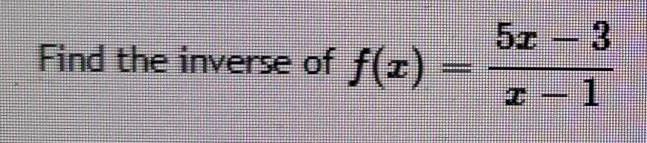

Math
FunctionsWhat are the domain and range of the relation? Is the relation a function?
F=((85,-16), (15,2), ( – 109,2), (70,42)}

Math
FunctionsLet ƒ(x) = (x + 6)².
Restrict the domain off to a non-decreasing interval.
Now find the inverse of f

Math
FunctionsFind the domain, any asymptotes, and the x- and y-intercepts of f(x). Then graph the function.
f(x)=2x+3/x

Math
FunctionsFor the function f(x), find the maximum number of real zeros, the maximum number of x-intercepts, and the maximum number of turning points that the function can have.
f(x)=x4-x³ +6
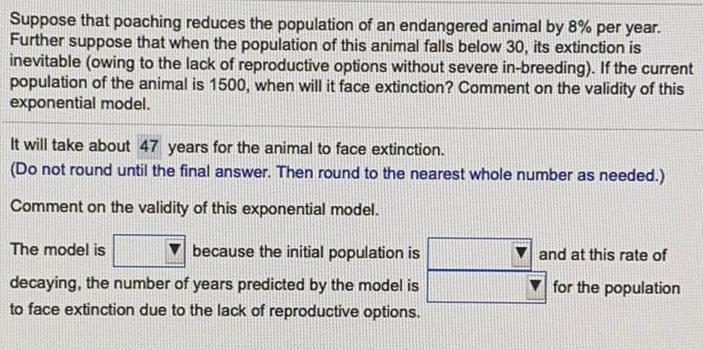
Math
FunctionsSuppose that poaching reduces the population of an endangered animal by 8% per year.
Further suppose that when the population of this animal falls below 30, its extinction is
inevitable (owing to the lack of reproductive options without severe in-breeding). If the current
population of the animal is 1500, when will it face extinction? Comment on the validity of this
exponential model.
It will take about 47 years for the animal to face extinction.
(Do not round until the final answer. Then round to the nearest whole number as needed.)
Comment on the validity of this exponential model.
The model is
because the initial population is
decaying, the number of years predicted by the model is
to face extinction due to the lack of reproductive options.
and at this rate of
for the population

Math
FunctionsDetermine if f(x) x5/4 - x + 1 is a polynomial function. If it is, state the degree
and the leading coefficient. If not, state why.
No. There is an exponent on a variable x that is not a whole number.
Yes. The degree is 5 and the leading coefficient is 114
No. The leading coefficient is not a whole number.
Yes. The degree is 5 and the leading coefficient is 1.

Math
FunctionsLet D= (x) x is the height above the ground) be the domain, and let f(x)= "time spent on a Ferris wheel" be the possible function. Determine if the relation is
an example of a function.
No, f is not a function.
Yes, f is a function.

Math
FunctionsThe position (in feet) of a buoy in the water can be modeled by the function
s(t) = 9 cos(t) where t is the elapsed time in seconds.
(a) If we start viewing the buoy when it is at its high point, how many seconds does it take
until the buoy is back at the high point again (i.e. What is the period of the function?)

Math
FunctionsChoose all that are properties of one-to-one functions.
x-values are repeated.
Functions are always one-to-one.
The graph passes the vertical line test.
y-values are repeated.
y-values are not repeated.
x-values are not repeated.
The graph passes the horizontal line test.
Math
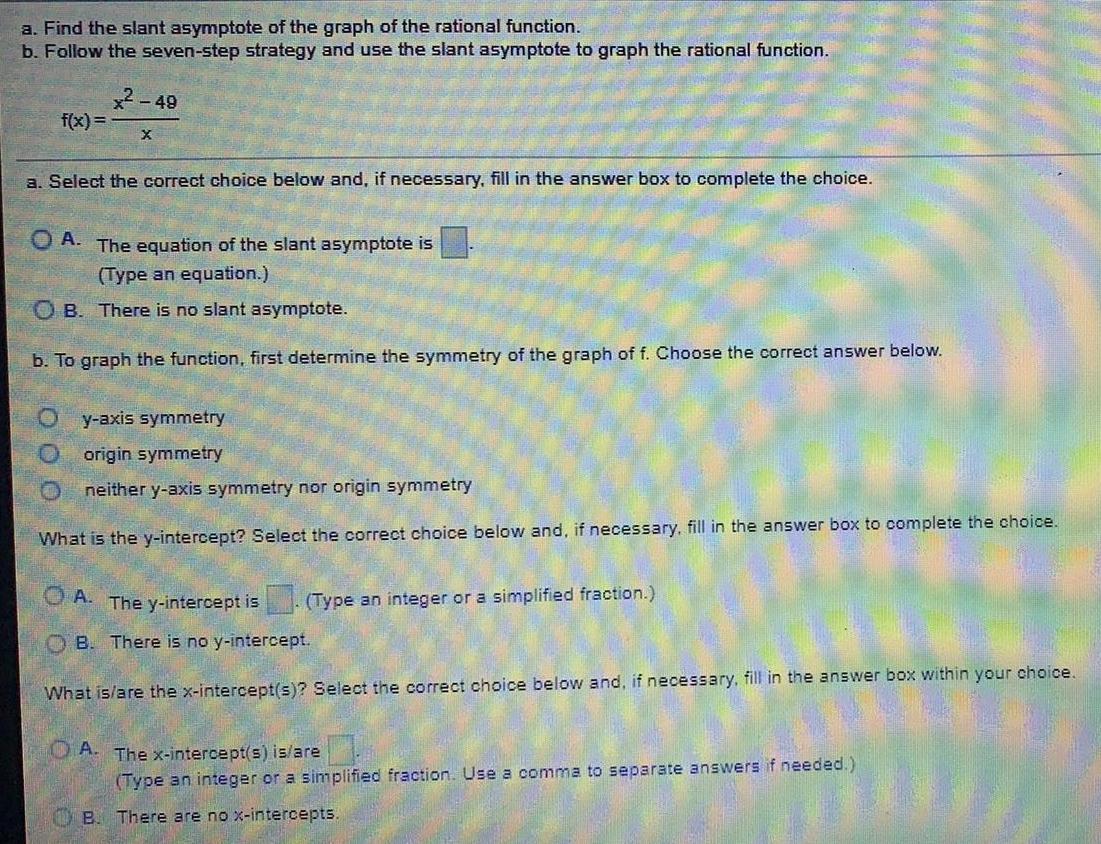
Functionsa. Find the slant asymptote of the graph of the rational function.
b. Follow the seven-step strategy and use the slant asymptote to graph the rational function.
f(x)=x^2-49/x
a. Select the correct choice below and, if necessary, fill in the answer box to complete the choice.
A. The equation of the slant asymptote is
(Type an equation.)
B. There is no slant asymptote.
b. To graph the function, first determine the symmetry of the graph of f. Choose the correct answer below.
y-axis symmetry
origin symmetry
neither y-axis symmetry nor origin symmetry
What is the y-intercept? Select the correct choice below and, if necessary, fill in the answer box to complete the choice.
A. The y-intercept is. (Type an integer or a simplified fraction.)
B. There is no y-intercept.
What is/are the x-intercept(s)? Select the correct choice below and, if necessary, fill in the answer box within your choice.
A. The x-intercept(s) is/are
(Type an integer or a simplified fraction. Use a comma to separate answers if needed.)
B. There are no x-intercepts.

Math
FunctionsThe function graphed to the right is of the form y = c + cos x, y = c + sinx,
y = cos (x-d), or y = sin (x-d), where d is the least possible positive value.
Determine the equation of the graph.

Math
FunctionsDescribe how the graph of g(x) =1/x+6 - 2 can be obtained from the graph of f(x) = 1/x.
How can the graph of g(x)= 1/x+6 -2 be obtained from the graph of f(x) = 1/x ?
A. Shift the graph left 6 units and up 2 units.
B. Shift the graph right 6 units and up 2 units.
C. Shift the graph left 6 units and down 2 units.
D. Shift the graph right 6 units and down 2 units.
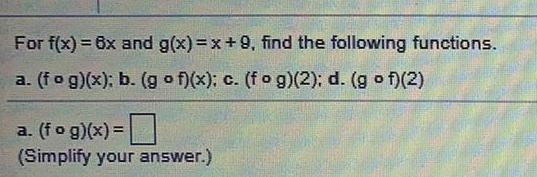
Math
FunctionsFor f(x) = 6x and g(x)=x+9, find the following functions.
a. (fog)(x); b. (gof)(x); c. (fog)(2); d. (gof)(2)
a. (fog)(x) =
Math
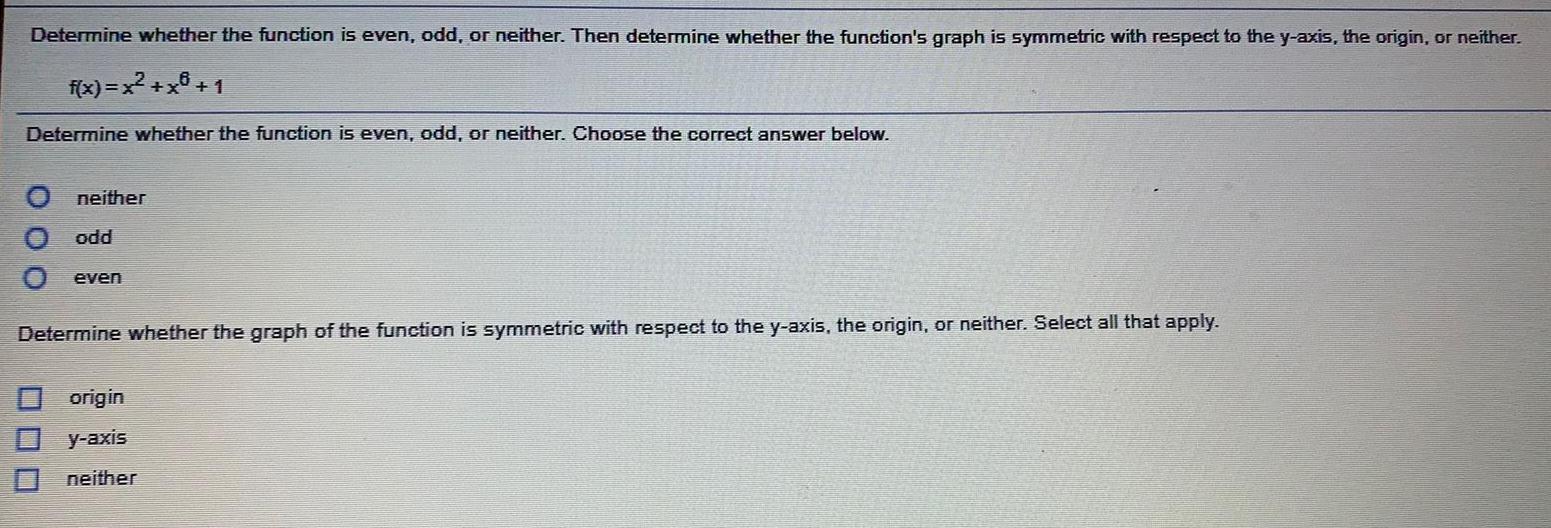
FunctionsDetermine whether the function is even, odd, or neither. Then determine whether the function's graph is symmetric with respect to the y-axis, the origin, or neither. f(x)=x²+x+1
Determine whether the function is even, odd, or neither. Choose the correct answer below.
neither
odd
even
Determine whether the graph of the function is symmetric with respect to the y-axis, the origin, or neither. Select all that apply.
origin
y-axis
neither
Math
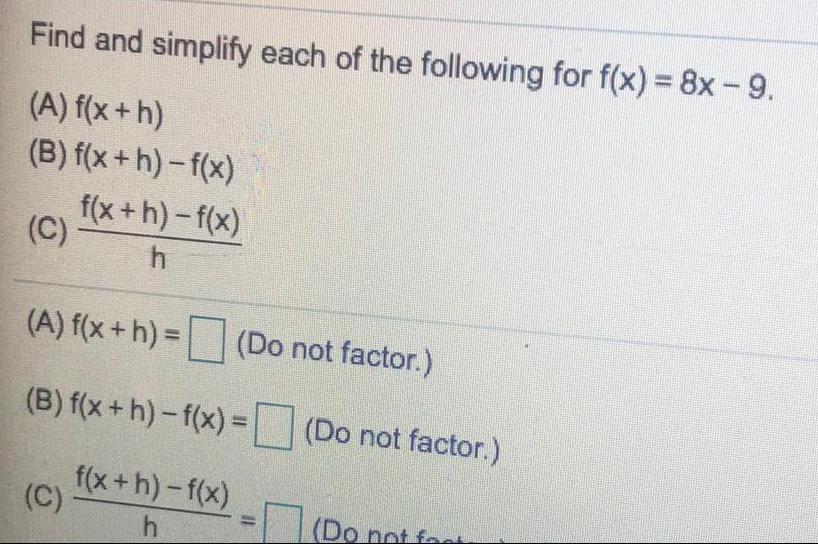
FunctionsFind and simplify each of the following for f(x) = 8x - 9.
(A) f(x + h)
(B) f(x+h)-f(x)
(C)f(x+h)-f(x)/h

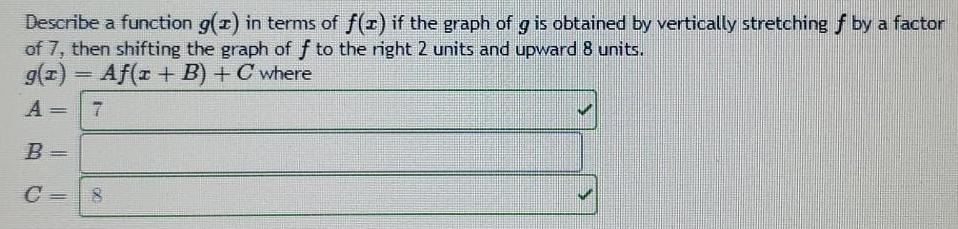
Math
FunctionsDescribe a function g(z) in terms of f(x) if the graph of g is obtained by vertically stretching f by a factor
of 7, then shifting the graph off to the right 2 units and upward 8 units.
g(x) = Af(x +B) + C where

Math
Functionsf(x) = -5(x + 4)(x − 3)(x + 1)³
a. How does the graph behave with relation to the x-axis at x=-1?
b. What are the real zeros of the function?
c. What is the degree of the function?
d. Describe the end behavior using limit notation.
e. Sketch a possible graph
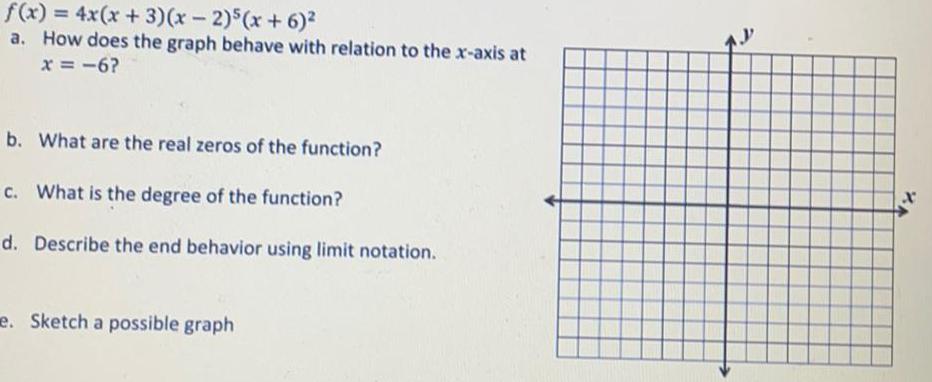
Math
Functionsf(x) = 4x(x + 3)(x - 2)5(x + 6)²
a. How does the graph behave with relation to the x-axis at x = -6?
b. What are the real zeros of the function?
c. What is the degree of the function?
d. Describe the end behavior using limit notation.
e. Sketch a possible graph

Math
FunctionsIf f(x) is an odd function, which statement about the graph of f(x) must be true?
It has rotational symmetry about the origin.
It has line symmetry about the line y = -x.
It has line symmetry about the y-axis.
It has line symmetry about the x-axis.

Math
FunctionsConsider the recursive function.
f(1) = 2
f(n) = 5 f(n-1), for n ≥ 2
Which statement is true?
A The value of f(6) is 2 times the value of f(3).
B The value of f(6) is 15 times the value of f(3). times the value of f(3).
C. The value of f(6) is
D. The value of f(6) is 125 times the value of f(3).
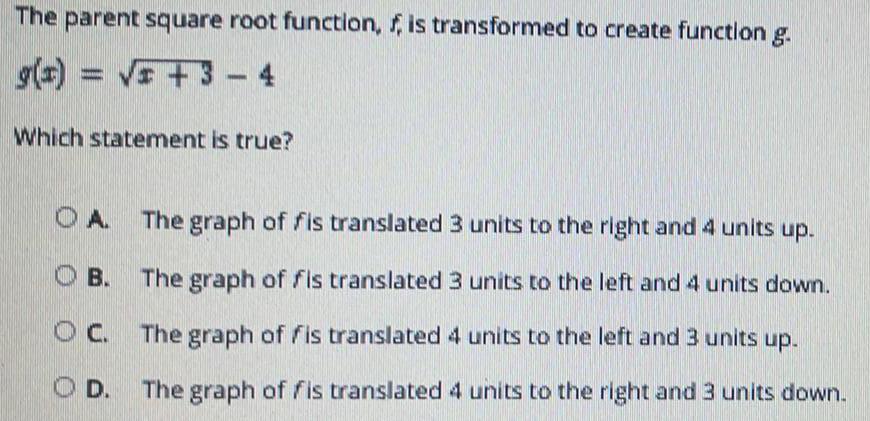
Math
FunctionsThe parent square root function, f, is transformed to create function g.
g(x)=√+3-4
Which statement is true?
A The graph of fis translated 3 units to the right and 4 units up.
B. The graph of fis translated 3 units to the left and 4 units down.
C. The graph of fis translated 4 units to the left and 3 units up.
D. The graph of fis translated 4 units to the right and 3 units down.

Math
FunctionsConsider these functions:
f(x)=3x³ + 2
g(x)=3√(x-2)/3
Which statements, if any, are true about these functions?
1. The function g(x)) = x for all real x.
II. The function g(x)) = x for all real x
III. Functions and g are inverse functions.
A. I only
B. II only
C. I, II, and III
D. None of the statements are true.

Math
FunctionsWhich statement is true about the graph of function f?
f(3) = log₂ #
A The graph has a horizontal asymptote of y = 0 and is decreasing as x approaches positive infinity.
B. The graph has a vertical asymptote of = 0 and is increasing as x approaches positive infinity.
C The graph has a vertical asymptote of = and is decreasing as x approaches positive infinity.
D. The graph has a horizontal asymptote of y = 0 and is increasing as x approaches positive infinity.

Math
FunctionsThe domain, range, and intercepts of a function are shown. Which set of information could be characteristics of the function's inverse? range: y2-1
x-intercept: (8,0)
domain: x2-2
y-intercept: (0,4)
A. domain: x2-1; range: yz -2; y-intercept: (0,8); x-intercept: (4,0)
B. domain: x2-1; range: y2 -2; y-intercept: (4,0); x-intercept: (0,8)
C domain: x2-2; range: y2-1; y-intercept: (0,8); x-intercept: (4,0)
D. domain: x2-2; range: yz-1; y-intercept: (0,4); x-intercept: (8,0)
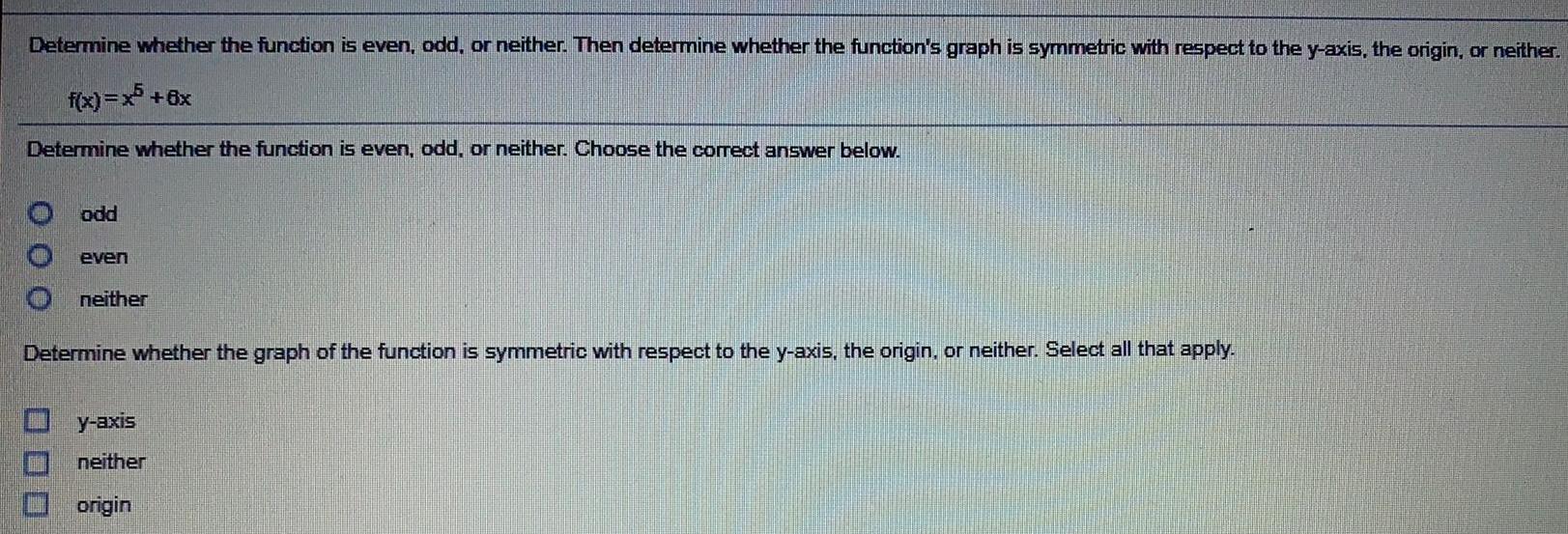
Math
FunctionsDetermine whether the function is even, odd, or neither. Then determine whether the function's graph is symmetric with respect to the y-axis, the origin, or neither.
f(x)=x5 +6x
Determine whether the function is even, odd, or neither. Choose the correct answer below.
odd
even
neither
Determine whether the graph of the function is symmetric with respect to the y-axis, the origin, or neither. Select all that apply.
y-axis
neither
origin