Functions Questions and Answers
Math
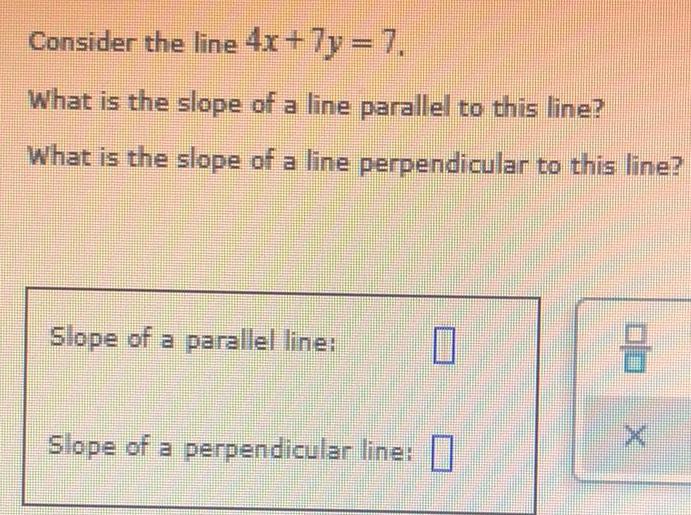
FunctionsConsider the line 4x + 7y = 7.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?

Math
FunctionsTheresa is comparing the graphs of y= 2^x and y = 5^x. Which of the following statements is TRUE?
A. Neither graph has a y-intercept.
B. Both graphs have a y-intercept of (0, 1), and y= 2^x is steeper.
C. Both graphs have a y-intercept of (0, 1), and y = 5^x is steeper.
D. The y-intercept of y= 2^x is (0, 2), and y-intercept of y 5^x is (0, 5).

Math
FunctionsWhich statement about the linear parent function is true?
A Its domain is the set of all non-negative numbers.
B Its range is the set of all real numbers.
C Its domain is the set of all negative rational numbers.
D Its range is the set of ordered pairs graphed in Quadrants I and IV.
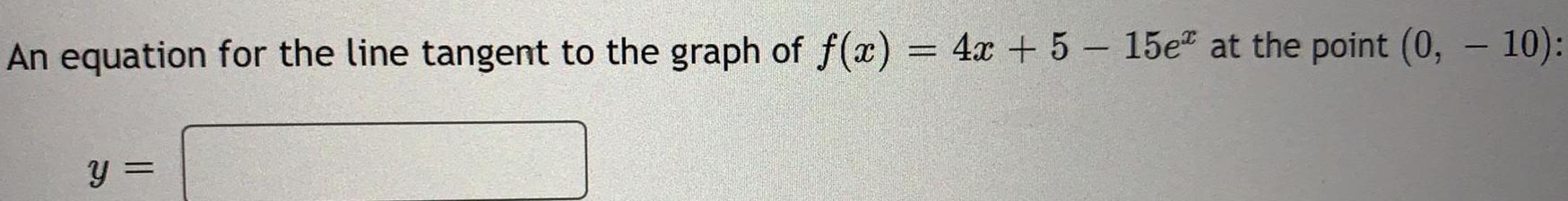
Math
FunctionsAn equation for the line tangent to the graph of f(x) = 4x + 5 - 15ex at the point (0, - 10):
Y =

Math
FunctionsThomas has graphed the function y = 7x-10 on a coordinate plane.
Which of the following statements is true for the function Thomas
graphed?
A. It has a slope of 10.
B. It has a y-intercept of 7.
C. It has a negative correlation.
D. It assigns exactly one output to each input.
Math
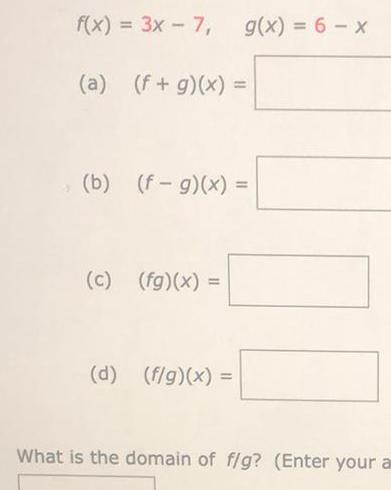
Functionsf(x) = 3x - 7, g(x) = 6 - x
(a) (f+g)(x) =
(b) (f-g)(x) =
(c) (fg)(x) =
(d) (f/g)(x) =
What is the domain of f/g?
Math
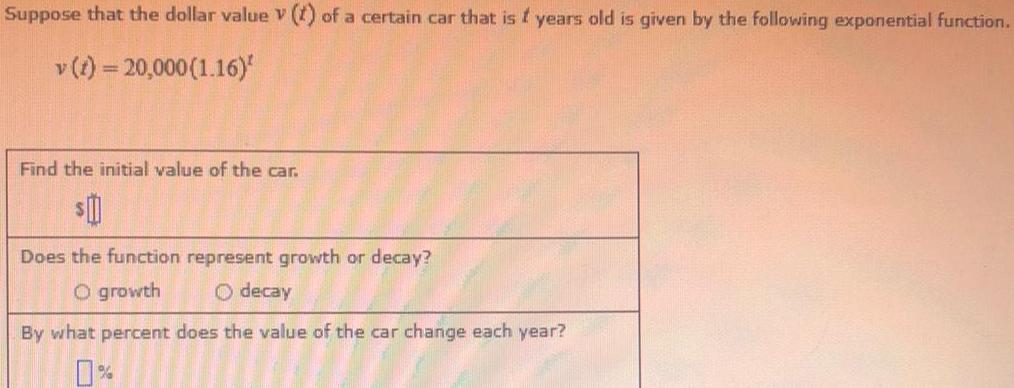
FunctionsSuppose that the dollar value V (t) of a certain car that is f years old is given by the following exponential function.
v (t) = 20,000 (1.16)^t
Find the initial value of the car.
Does the function represent growth or decay?
growth
decay
By what percent does the value of the car change each year?
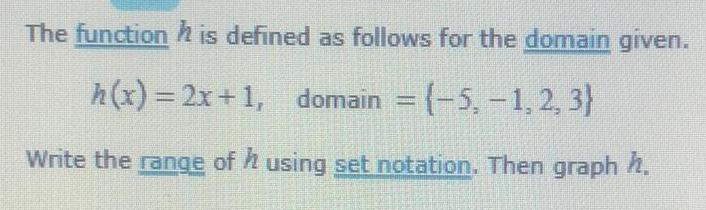
Math
FunctionsThe function is defined as follows for the domain given.
h(x) = 2x+1, domain = (-5, -1, 2, 3)
Write the range of h using set notation. Then graph h.

Math
FunctionsIf the parent function is f (x) = log5 (x), identify the transformations of the parent function given f (x) = -5 log5 (x+2)-3. (select all that apply)
A vertical stretch of 5
B vertical shift down 3
c vertical compression of 1/5
D reflection over the y-axis
E horizontal shift left 2
F reflection over the x-axis
G horizontal shift right 2
H vertical shift up 3

Math
FunctionsAlgebraically find the vertex & build a table of 5 values for the following absolute value function: y = 3x - 1| +7

Math
FunctionsDescribe how the change would affect the graph of f(x) = x².
f(x) = x² + 2
If it is shifted to the left 4 units, you would write "left four" with no quotes.
If it is compressed or stretched, write "compressed" or "stretched" with no quotes.
If it is reflected over the x-axis, type "reflected" with no quotes.

Math
FunctionsIf the Laffite family deposits $8,500 in a savings account at 6.75% Interest, how much will the account make after 25 years if it is compounded...
a) monthly?
b) weekly?
c) continuously?
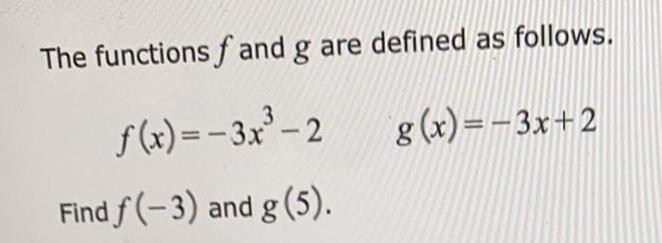
Math
FunctionsThe functions fand g are defined as follows.
f(x)=-3x³-2 g(x)=-3x+2
Find f(-3) and g (5).
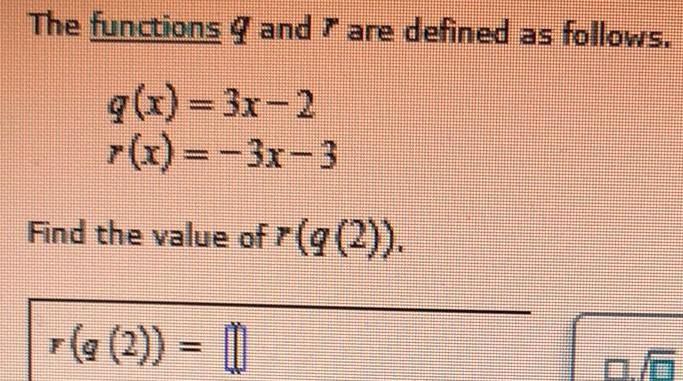
Math
FunctionsThe functions and are defined as follows.
q(x)=3x-2
r(x)=-3x-3
Find the value of r(q (2)).

Math
FunctionsA relation contains the points (1, 2), (2, -1), (3, 0), (4, 1), and (5,-1). Which statement accurately describes this relation?
F The relation does not represent y as a function of x, because each value of x is associated with a single value of y.
G The relation represents y as a function of x, because one value of y is associated with two values of x.
H The relation does not represent y as a function of x, because each value of y is associated with two values of x.
J The relation represents y as a function of x, because each value of x is associated with a single value of y.

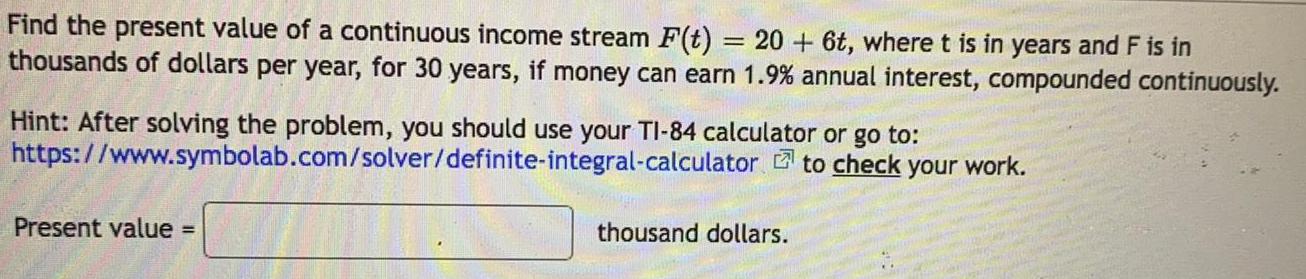
Math
FunctionsFind the present value of a continuous income stream F(t) = 20 + 6t, where t is in years and F is in thousands of dollars per year, for 30 years, if money can earn 1.9% annual interest, compounded continuously.

Math
FunctionsGiven the demand function d(p) = 27 – p², and the supply function s(p) = 6p.
Calculate the following:
a) The equilibrium price:
b) The gains from trade is the sum of the consumer and producer surplus. Calculate the gains from trade
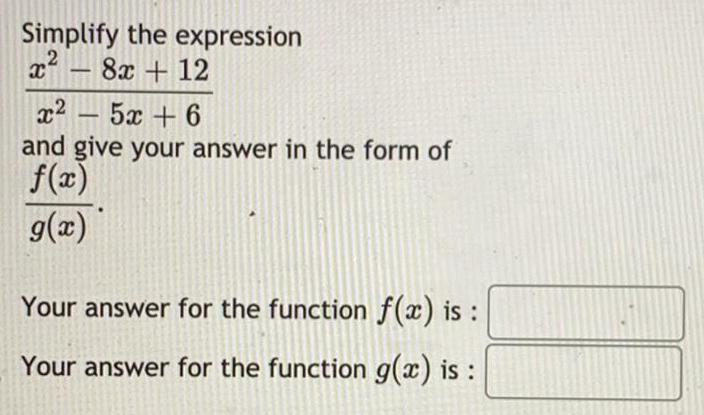
Math
FunctionsSimplify the expression
x^2- 8x +12 / x^2- 5x + 6
and give your answer in the form of
f(x)/g(x)
Your answer for the function f(x) is :
Your answer for the function g(x) is:

Math
FunctionsA chemist weighs samples obtained from a production run. The weights of the samples are 11 g, 10 g, 6 g. 11 g. 15 g. 13 g. 14 g, 12 g. 13 g. 12 g, 14 g, and 18 g. find the outlier(s) if there are
any. Describe how any outlier affects the mean and the standard deviation.
Q1-1.5(IQR)
Q3+1.5(IQR)

Math
FunctionsA) The luxury tax threshold in a professional sports league is the amount in total payroll that teams must stay under to prevent being levied a competitive balance tax by the league's commissioner. One model that could be used to represent the amount of the league's luxury threshold A, in millions of dollars, t years since 2003 is A (t) = 120(1.033)'. Suppose a second model assumed that the league's luxury threshold was $117 million in 2003 and increased by 3.5% each year. How would the function A (t) change to represent the second model? (1 point)
The coefficient changes from 120 to 103.5, and the base changes from 1.033 to 0.17. The function that represents the second model is A (t) = 103.5(0.17t).
The coefficient changes from 120 to 103.5, and the base changes from 1.033 to 1.17. The function that represents the second model is A (t) = 103.5(1.17)t.
The coefficient changes from 120 to 117, and the base changes from 1.033 to 0.035. The function that represents the second model is A (t) = 117(0.035)t.
The coefficient changes from 120 to 117, and the base changes from 1.033 to 1.035. The function that represents the second model is A (t) = 117(1.035)t.

Math
FunctionsSuppose a company has fixed costs of $31,200 and variable costs of 1/3x2+444x dollars, where x is the total number of units produced. Suppose further that the selling price of its product is 1768- 2/3x dollars per unit.
(a) Find the break-even points. (Enter your answers as a comma-separated list.)
x=24,1300
(b) Find the maximum revenue. (Round your answer to the nearest cent.)
(c) Form the profit function P(x) from the cost and revenue functions.
P(x) = -x² +1324x-31200
Find maximum profit.
$ 407044
(d) What price will maximize the profit? (Round your answer to the nearest cent.)

Math
FunctionsConsider the acceleration function of an object on a projectile motion
is a (t) = -32.
If v (0) = 28 ft/sec and s (0) = 120, what is the maximum height of the object in feet?

Math
FunctionsIn 2003, David received $10,000 from his grandmother. His parents invested all of the money, and by 2015, the amount will have grown to $16,958.81. Use the exponential function y = 10000 1.045* where y is the amount in the account and x is the number of years since 2003. Assume that the amount of money continues to grow at the same rate. What would be the balance in the account in 2025?

Math
FunctionsCaptain Ahab needs $6000.00 worth of harpoons. He started with $1500.00 and has been saving $350 a week to buy the harpoons. Write a function that illustrates this situation.
Function: h(x)=
Slope/Meaning in context: m =
y-intercep/Meaning in context: b =
How much will Captain Ahab have saved after seven weeks?
How many weeks will it take the captain to buy the harpoons he needs? Write an equation to model this situation and solve.

Math
FunctionsGraph the equation y=x+5. Let x = -3, -2, -1, 0, 1, 2, and 3.
Find the following y-values. Then choose the correct graph of the equation to the right.
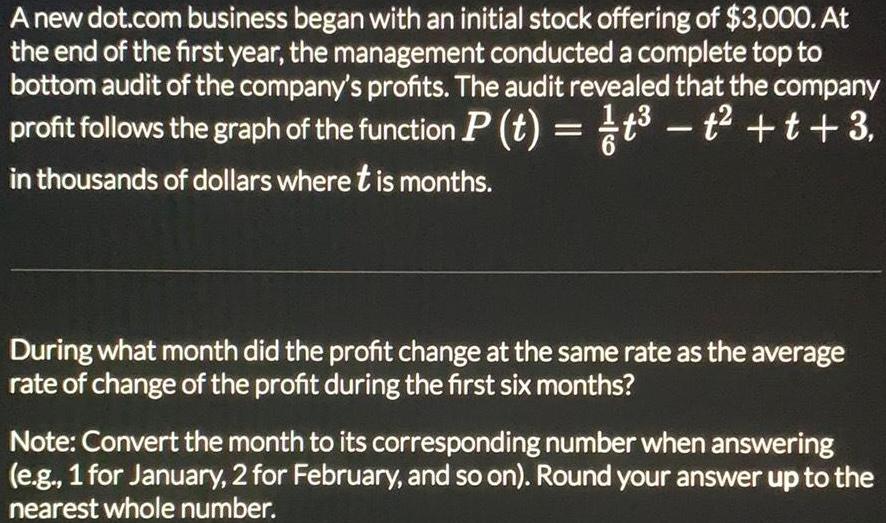
Math
FunctionsA new dot.com business began with an initial stock offering of $3,000. At the end of the first year, the management conducted a complete top to bottom audit of the company's profits. The audit revealed that the company profit follows the graph of the function P (t) = t³ - ² +t+ 3,
in thousands of dollars where t is months.
During what month did the profit change at the same rate as the average rate of change of the profit during the first six months?
Note: Convert the month to its corresponding number when answering
(e.g., 1 for January, 2 for February, and so on). Round your answer up to the
nearest whole number.

Math
FunctionsThe town of Frostbite Falls records its population at the end of a given year as 70,000. After 1 year, the population increases by 2.4%. After the next year, the population again increases by 2.4%, and the pattern continues each year. What is the y-intercept of the exponential function that models this growth? (1 point)
The y-intercept is (0, 0).
The y-intercept is (0, 2.4).
The y-intercept is (0, 70, 000).
The y-intercept is (70, 000, 0)
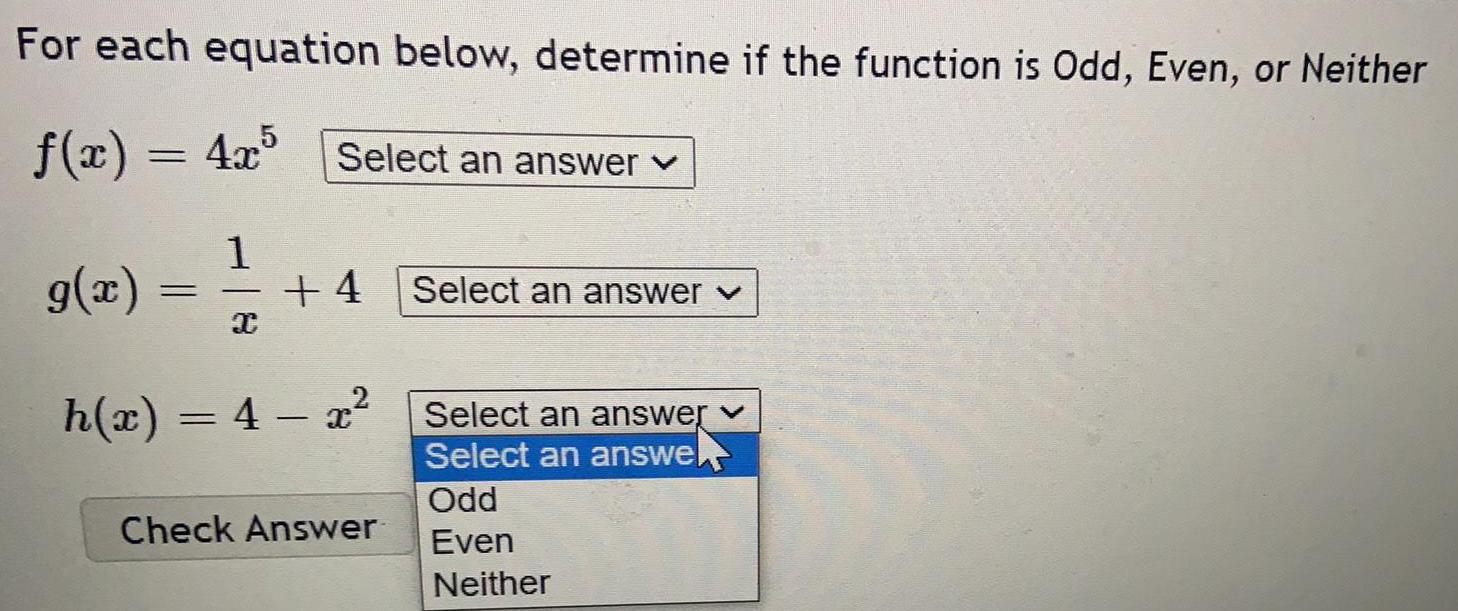
Math
FunctionsFor each equation below, determine if the function is Odd, Even, or Neither
f(x) = 4x^5
g(x) = 1/x + 4
h(x) = 4 - x²

Math
FunctionsWhich best describes the numbers satisfying the inequality x<7?
all numbers greater than 7
all numbers less than 7
all numbers greater than and including 7
all numbers less than and including 7

Math
FunctionsGraph the inverse of the function f(x) = 2x+4. Show the function and its inverse on the same coordinate plane. Your answer must include:
• A hand-drawn or calculator-created image of the graphs with the functions f(x) and f1(x) identified, along with labeled axes.
• A table of values with at least six ordered pairs for each function, f(x) and f¹(x).
. An explanation of the reason these functions are inverses. Use complete sentences.
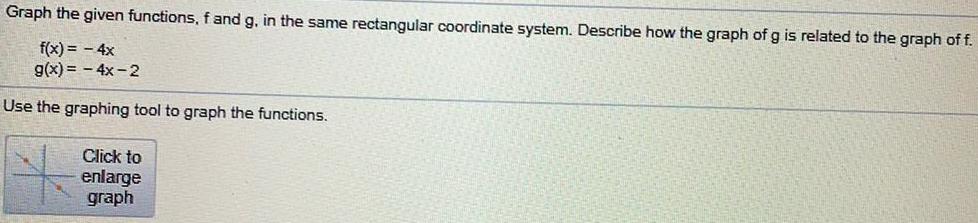
Math
FunctionsGraph the given functions, f and g, in the same rectangular coordinate system. Describe how the graph of g is related to the graph of f.
f(x) = - 4x
g(x)=-4x-2
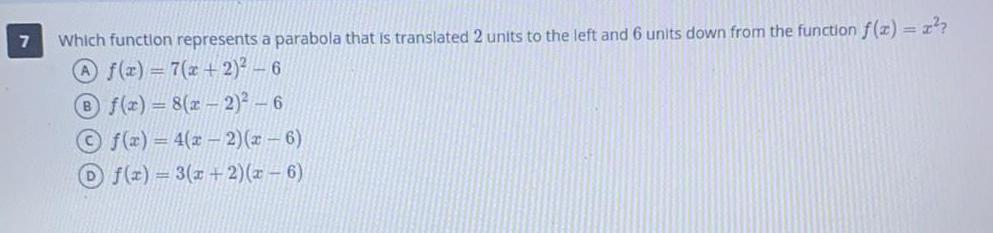
Math
FunctionsWhich function represents a parabola that is translated 2 units to the left and 6 units down from the function f(x) = x²?
A f(x) = 7(x + 2)²-6
B f(x) = 8(x - 2)²-6
C f(x) = 4(x-2)(x-6)
D f(x)=3(x+2)(x-6)

Math
FunctionsFind a polynomial function f(x) with the given degree, zeros, and leading coefficient:
Degree 4, x = - 3, multiplicity of 2; x = 1 multiplicity of 1; x = 3, multiplicity of 1 and a leading
coefficient of 1.
a) The factored form is:
b) Find the polynomial equation in standard form.
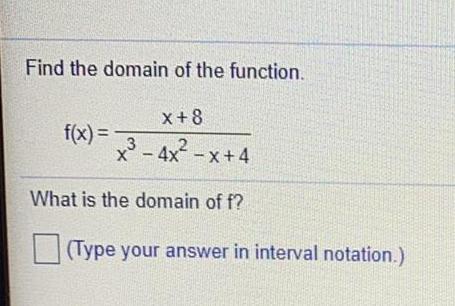
Math
FunctionsFind the domain of the function.
f(x) = x+8/x³-4x²-x+4
What is the domain of f?
(Type your answer in interval notation.)
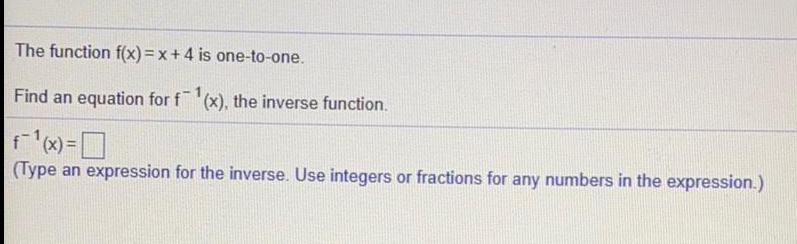
Math
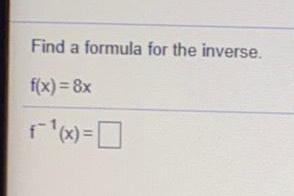
FunctionsThe function f(x)=x+4 is one-to-one.
Find an equation for f-1(x), the inverse function.
(Type an expression for the inverse. Use integers or fractions for any numbers in the expression.)
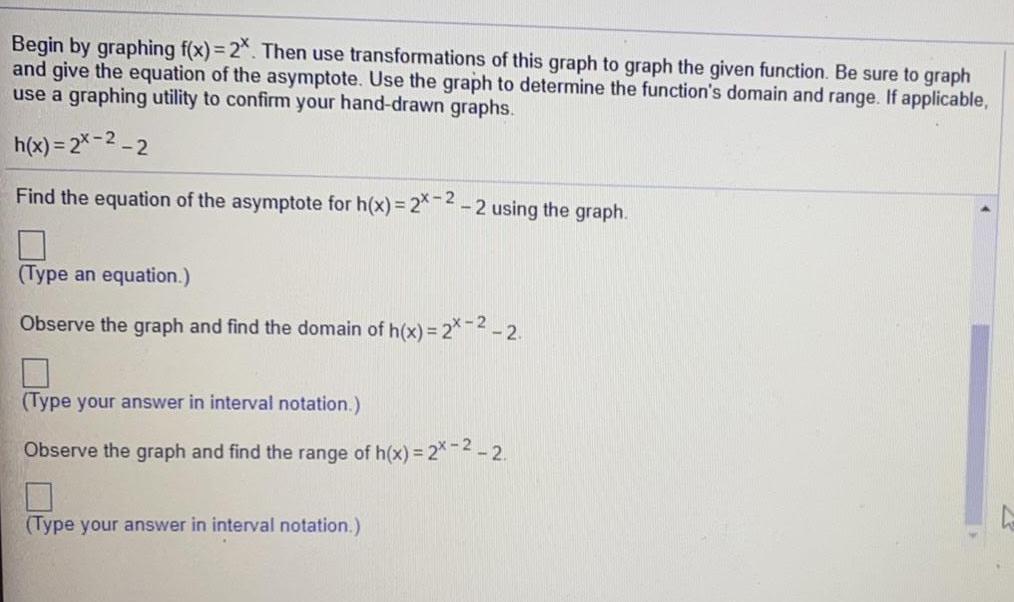
Math
FunctionsBegin by graphing f(x)=2*. Then use transformations of this graph to graph the given function. Be sure to graph and give the equation of the asymptote. Use the graph to determine the function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. h(x)=2x-2-2
Find the equation of the asymptote for h(x)=2x-2-2 using the graph.
(Type an equation.)
Observe the graph and find the domain of h(x) = 2*-2 -2.
(Type your answer in interval notation.)
Observe the graph and find the range of h(x)=2x-2-2.
(Type your answer in interval notation.)
Math
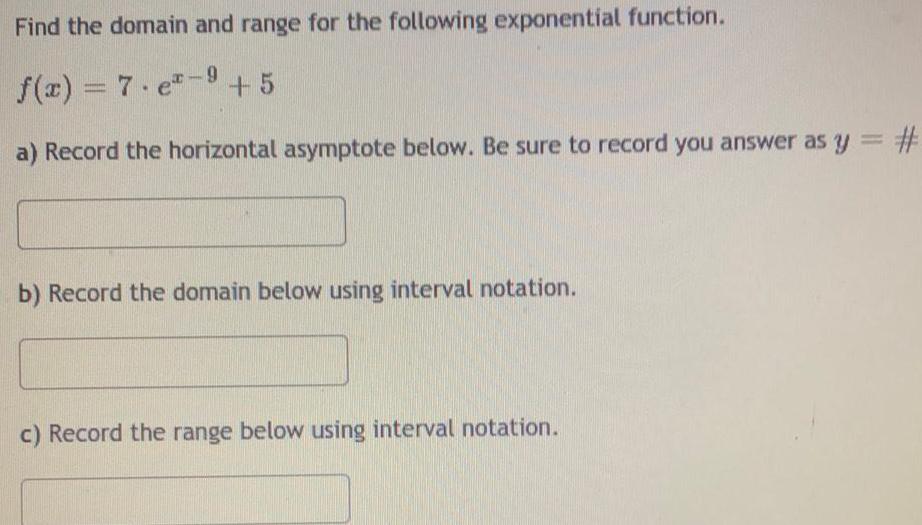
FunctionsFind the domain and range for the following exponential function.
f(x) = 7.e-9 +5
a) Record the horizontal asymptote below. Be sure to record you answer as y = #
b) Record the domain below using interval notation.
c) Record the range below using interval notation.

Math
FunctionsDescribe a situation with an output of area in square feet that can be modeled using the function f(x) = (x)(2x + 5).

Math
FunctionsAn orange is shot up into the air with a catapult. The function h given by h(t) = 15+ 60t - 16t² models the orange's height, in feet, t seconds after it was launched.
Select all the true statements about the situation.
a. The domain of function h only contains values greater than or equal to 0.
b. The orange is at the same height 1 second after launch and 2 seconds after launch.
c. After 3 seconds, the orange has hit the ground.
d. The orange is 15 feet above the ground when it is launched.
e. The value t =10 does not belong to the domain of h.

Math
FunctionsMia opens a coffee shop in the first week of January. The function W(x) = 0.002x3 -0.01x2 models the total number of customers visiting the shop since it opened after x days. She then opens an ice cream parlor in the month of February. The function R(x) = x2 - 4x + 13 models the total number of customers visiting the parlor since it opened after x days.
Which function represents the difference of the number of customers visiting the two shops?
A. D(x) = 0.002x3 +1.01x2 - 4x + 13
B. D(x) = 0.002x3 - 1.01x2 + 4x - 13
C. D(x) = 0.002x3 - 0.99x2 - 4x + 13
D. D(x) = 0.002x3 +0.99x2 + 4x - 13

Math
FunctionsDrag the values to the correct locations on the image. Not all values will be used.
Function fis a logarithmic function with a vertical asymptote at x = 0 and an x-intercept at (4,0). The function is decreasing over the interval (0,infinity).
Function g is represented by the equation g(x)= log₂ (x + 3) - 2
Over which interval are both functions positive?

Math
FunctionsWhich function defines (g - f)(x)?
f(x) = 3√12x + 1 + 4
g(x) = log(x − 3) + 6
A. (g-f)(x) = log x - 3√12x - 12
B. (g - f)(x) = log(x − 3) - 3√12x+1 - 10
C. (g - f)(x) = log(x - 3) - 3√12x+1 + 2
D. (g - f)(x) = log(x - 3) - 3√12x+1 +10

Math
FunctionsWhich statement best demonstrates why the following is a non-example of a polynomial?
33y² /x²-62y2xz-35z2y2
The expression has a variable raised to a negative exponent.
The expression has a negative coefficient.
The expression has a variable raised to a fraction.
The expression has a variable in the denominator of a fraction.

Math
FunctionsA sample of a radioactive isotope had an initial mass of 540 mg in the year 2009 and decays exponentially over time. A measurement in the year 2011 found that the sample's mass had decayed to 300 mg. What would be the expected mass of the sample in the year 2021, to the nearest whole number?

Math
FunctionsA sample of a radioactive isotope had an initial mass of 560 mg in the year 1995 and decays exponentially over time. A measurement in the year 2002 found that the sample's mass had decayed to 90 mg. What would be the expected mass of the sample in the year 2012, to the nearest whole number?

Math
FunctionsAn object dropped from a tower has its height in feet above the ground t seconds into the fall given by s(t) = 160 -16t2. Include appropriate units in your answers to all questions:
a) What is the object's velocity, speed, and acceleration at time t?
b) How long does it take the object to hit the ground?
c) What is the object's velocity at the moment of impact?


Math
FunctionsWhich function defines(ƒ ÷ g)(x),
ƒ(1) = (3.6)x+2
g(x) = (3.6)³x+1
A (g ÷ f)(x) = (1.8)3x²+7+2
B. (g = f)(x) = (1.8)−2x+3
C. (g ÷ 1)(x) = (3.6)4x+3
D. (g = f)(x) = (3.6)-2x+1