Functions Questions and Answers

Math
FunctionsWhich statement best describes the end behavior of the following function?
F(x) = 2x²-x² +5x-9
A. The graph of the function starts low and ends low.
B. The graph of the function starts high and ends low.
C. The graph of the function starts high and ends high.
D. The graph of the function starts low and ends high

Math
FunctionsSelect all that describe the graph of f(x) = 1/3 4x as compared to the graph of f(x) = 4x
vertical compression
exponential growth
reflected over the y-axis
reflected over the x-axis
vertical stretch
exponential decay

Math
FunctionsSelect the equations that represent an Exponential Growth Equation.
(Choose 2)
f(x) = 1/3(1/2) x
f(x) = 2(1/5)x
f(x) = 1/5(3/2)x
f(x) = 2(3)x

Math
FunctionsSelect all that describe the graph of f(x) = 3(1/2)x-4-2 as compared to f(x) = ()*.
(Choose 3)
horizontal shift to the right 4
Overtical compression
vertical stretch
vertical shift up 2
vertical shift down 2
horizontal shift to the left 4


Math
FunctionsWhat is the output of the following function for x = 2?
F(x) = 2x¹ - x³ +5x-9
A. 25
B. 11
C. 9
D. 14

Math
FunctionsWhat are the domain and range of the function represented by the set of
ordered pairs?
{(-13, 9), (-7,-5), (5, 14), (11, -10)}
A. Domain: {-13, -7, 5, 11}
Range: (-10,-5, 9, 14)
B. Domain: {-10, -5, 9, 14)
Range: (-13, -7, 5, 11)
C. Domain: -13 ≤x≤ 11
Range: -10y≤ 14
D. Domain: -10 ≤ x ≤ 14
Range: -13 sys11
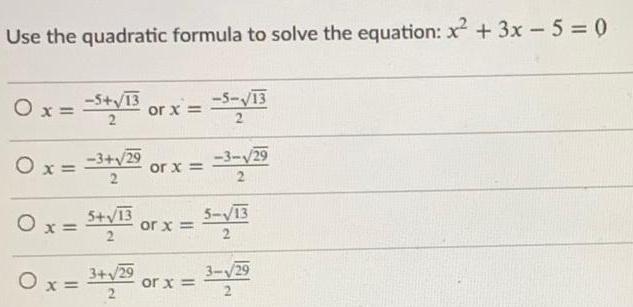
Math
FunctionsUse the quadratic formula to solve the equation: x² + 3x - 5 = 0
x = -5 + √13/2 or x = -5-√13/2
x = -3+√29/2 or x = -3-√29/2
x = 5+√13/2 or x = 5-√13/2
x = 3+√29/2 or x = 3-√29/2

Math
Functionsf(x)=√x - 11. Find the inverse of f(x) and its domain.
A. f¹(x) = x² +11; x2-11
B. ƒ ¹ (x) = (x + 11) ² ; x ≥ 0
C. ƒ ¹ (x) = x² + 11; x ≥ 0
D. f¹(x) = (x +11)²; x2-11
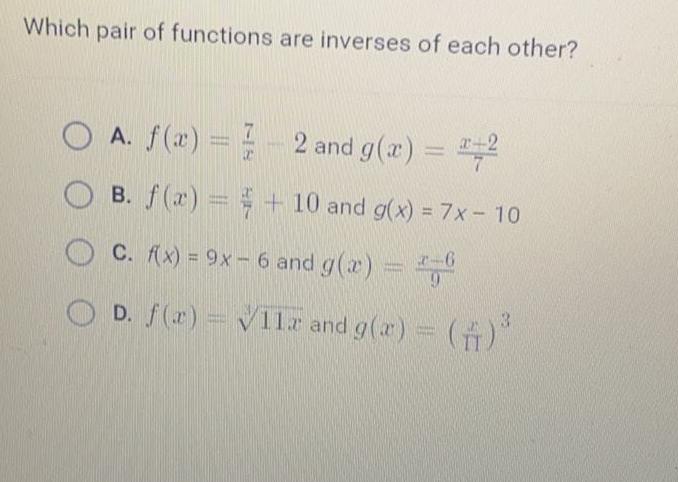
Math
FunctionsWhich pair of functions are inverses of each other?
A. f(x) = 7/x - 2 and g(x) = x+2/7
B. f(x) = x/7 + 10 and g(x) = 7x - 10
C. f(x) = 9x - 6 and g(x) = x-6/9
D. f(x)= 3√11x and g(x) = (x/11)³

Math
FunctionsFor - 11 ≤ x ≤ 13 the function f is defined by f(x) = x³ (x + 1)²
On which two intervals is the function increasing (enter intervals in ascending order)?
Find the interval on which the function is positive:
Where does the function achieve its minimum?

Math
Functionsf(x) = 4x² + 3x - 2
g(x) = 6x³ – 3x² - 4
Find (f + g)(x).
A. (f+g)(x) = 10x³ - 6
B. (f+g)(x) = 6x³ + 7x² + 3x + 2
C. (f+g)(x) = 6x³ + 4x² 6
D. (f+g)(x) = 6x³ + x² + 3x 6
![A trigonometric function models the monthly rainfall of a city, which reaches a maximum monthly rainfall of 8 inches in the spring and fall and a minimum monthly rainfall of 0 inches in the summer and winter. if(t) models the monthly rainfall & months from when the monthly rainfall started being recorded for the city, what is the domain of function r ?
A. [0, 8]
B. (-∞, ∞)
C. [0, ∞)
D. [8,∞]](https://media.kunduz.com/media/sug-question/raw/50729759-1658392890.8984075.jpeg?w=256)
Math
FunctionsA trigonometric function models the monthly rainfall of a city, which reaches a maximum monthly rainfall of 8 inches in the spring and fall and a minimum monthly rainfall of 0 inches in the summer and winter. if(t) models the monthly rainfall & months from when the monthly rainfall started being recorded for the city, what is the domain of function r ?
A. [0, 8]
B. (-∞, ∞)
C. [0, ∞)
D. [8,∞]

Math
FunctionsA retailer is having a promotional sale for 35% off all items. There is a 7% sales tax added to the price. Which represents the situation, where x is the original cost of the item(s)?
f(x) = 0.35x represents the discount price and g(x)=0.07x represents the price after taxes. The total price would be (f.g)(x) = 0.35(0.07x) = 0.0245x.
f(x) = 0.65x represents the discount price and g(x)=0.07x represents the price after taxes. The total price would be (f.g)(x) = 0.65(0.07x)=0.0455x.
f(x) = 1.07x represents the price after taxes and g(x) = 0.65x represents the discount price. The total price would be (f.g)(x) = 1.07(0.65x)=0.6955x.
f(x) = 1.07x represents the price after taxes and g(x) = 0.35x represents the discount price. The total price would be (f.g)(x) = 0.35(1.07x) = 0.3745x.

Math
FunctionsWhich function displays this end behavior?
As x approaches negative infinity, y approaches negative infinity.
As x approaches positive infinity, y approaches negative infinity.
A y = (2x)^1/3 - 7
B. y = -3x^2 + 4
C. y = -2x^3 - 1
D. y = -x^1/2 + 5

Math
FunctionsFor the real-valued functions g(x)=x²+3 and h(x)=x-4, find the composition goh and specify its domain using interval notation.

Math
FunctionsThe functions f and g are defined by f(x) = 8x +33 and g(x) = 2 - (1.2).
1. Which function eventually grows faster, for g? Explain how you know.
2. Explain why the graphs of f and g meet for a positive value of x.

Math
FunctionsConsider a function f(x) = x². A second function h(x) is the result of reflecting f(x) across the x axis and translating it 3 units in the positive y-direction (upward). Write the equation of h(x).

Math
FunctionsWrite a rule for g that represents the indicated transformations of the graph of f
g (z) = A tan B (x - C) + D
ƒ(x) = 1/6 tan (x): Translation 6 units down, 4 units left, then reflected over the line y = -6

Math
FunctionsUsing interval notation, identify the domain for the function: f(x)=2x+1/ x-4
(-∞,∞)
(-∞,4)U(4,∞)
(-∞,-4)U(4,∞)
(-∞,2)U(2,∞)

Math
FunctionsUse the remainder theorem to find P (3) for P(x) = -x + 3x³-x+5.
Specifically, give the quotient and the remainder for the associated division and the value of P (3).

Math
FunctionsA vehicle factory manufactures cars. The unit cost C (the cost in dollars to make each car) depends on the number of cars made. If x cars are made, then the unit cost is given by the function C(x)=0.8x²-352x+49,032. How many cars must be made to minimize the unit cost?
Do not round your answer.

Math
FunctionsWhich of the following functions have an amplitude of 4 and a period of 2? Select all that apply.
y = 4 cos 2x
y=2 sin 4x
y = 4 сos πx

Math
FunctionsFind the difference quotient f(x+h)-f(x)/h where h#0, for the function below.
f(x)=-3x²+6x-9
Simplify your answer as much as possible.

Math
FunctionsFor the real-valued functions f(x)=√2x+4 and g(x)=x-1, find the composition f.g and specify its domain using interval notation.
(f.g)(x) =
Domain of f g :

Math
FunctionsThe functions f and g are defined as follows.
f(x)=x²-x-2 and g(x)= 7x-3/5x-1
Find f(x+8) and g(x/4)
Write your answers without parentheses and simplify them as much as possible.

Math
FunctionsThe functions f and g are defined as follows.
f(x)=x²+9x+5 and g(x)= 3/ x²-2
Find f(x-3) and g(-/x)

Math
FunctionsThe functions f and g are defined as follows.
f(x)=4x+3/5x+2
and g(x)=√x^2-8x
Write your answers without parentheses and simplify them as much as possible.
Find f(1/x)
and g(x-2).

Math
FunctionsThe area A (r) (in square meters) of a circular algae colony with radius r meters is given by A (r) =πr².
The radius M (t) (in meters) after t minutes is given by M (t) = 10/3 t.
Write a formula for the area Z (t) (in square meters) of the algae colony after t minutes.
![Use interval notation to represent all values of x satisfying the given conditions.
f(x) = 5x-4, g(x) = 4x-6, and f(x) > g(x)
A. (-10,00)
B. (-∞0.-2]
C. (-2,00)
D. [-2.00)](https://media.kunduz.com/media/sug-question/raw/49942521-1658341592.301305.jpeg?w=256)
Math
FunctionsUse interval notation to represent all values of x satisfying the given conditions.
f(x) = 5x-4, g(x) = 4x-6, and f(x) > g(x)
A. (-10,00)
B. (-∞0.-2]
C. (-2,00)
D. [-2.00)

Math
FunctionsWrite the quadratic equation with the following transformations:
Reflected over the x-axis
Vertical shrink of 1/3
Translated up 2 units
y = -3(x + 2)²
y = -(1/3)x² + 2
y = -(1/3)(x + 2)²
y = -3x² + 2

Math
FunctionsLet f(x)=x³-4x²+7x-6/x-2
a. Graph the function on the window xmin = -2, xmax = 4, ymin = 0,
ymax = 10.
b. What is the domain of the function?
c. Find lim x⇒2 f(x).
d. Write a very short paragraph about the importance of examining a function
analytically as well as graphically.
e. In light of part b, make sure your graph is correct.

Math
FunctionsFind each indicated quantity if it exists. Let f(x) = |x-11| / x-11 .Complete parts (A) through (D).
(A) Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. lim f(x)= (Simplify your answer.)
B. The limit does not exist.

Math
FunctionsThe equation y = 8x + 12, where x is the number of
hours and y is the total cost, represents what the surf
instructor charges for lessons. Use this information to
describe how to draw the line on a graph.

Math
FunctionsThe graph of:
y = 11x³ + 22x² + 14x / (5x² + 1)(11x + 7)
has one vertical asympote and one horizontal asymptote.
An equation for the vertical asymptote is:
An equation for the hoizontal asymptote is:

Math
Functions9/7x+35=9/x+5-6/7
aWhat is/are the value or values of the variable that make(s) the denominators zero?
x=
(Simplify your answer. Use a comma to separate answers as needed.)
b. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A The solution set is {}.
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)
B. The solution set is {x) x is a real number}.
C. The solution set is Ø.

Math
FunctionsFor the function g(x)=1/2x-4, find g(2) + g(a).
g(2)+g(a) = (Use integers or fractions for any numbers in the expression.)

Math
FunctionsVictoria read a 160-page historical fiction novel followed by a science fiction novel of the exact same length. Her average reading speed of the science fiction novel was 2 pages per hour more than her average reading speed of the historical fiction novel. Victoria models her novel reading marathon with the following expression, where x represents her average reading speed of the historical fiction novel. What does x + 2 represent in this situation?
A. the average reading speed of the science fiction novel
B. the number of pages of the science fiction novel
C. the average reading speed of the historical fiction novel
D. the total time taken to read the novels

Math
FunctionsEnter the correct answer in the box.
The graph of function g is created by applying these transformations to the parent tangent function:
reflection over the x-axis
• horizontal stretch by a factor of 5
• vertical shift down 3 units
Write the equation representing function g.

Math
FunctionsThe exponential function f(x) = 2500(0.4) models the amount of money in Zachary's savings account over the last 10 years. Is Zachary's account balance increasing or decreasing? Write the base in terms of the rate of growth or decay.

Math
FunctionsAn investment of $1800 earns 6% annual interest, compounded monthly.
What is an appropriate unit of time (such as days, weeks, years)?
What is the multiplier that should be used?
What is the initial value?
What is an exponential equation in the form y = a(b)* that can be used to model the

Math
FunctionsEmma says that for f(x) = 8,000(0.95)*, the exponential growth is 0.95 and the y-intercept is 8,000. What is her error?
Choose the correct answer below and fill in the answer box(es) to complete your choice.
Since b =
A. For f(x) to be an exponential growth model, a>
it should be exponential decay, not growth.
B. In an exponential growth model y = a. bx, the exponential growth r is found using the equation r= 1-b. So, the exponential growth is
and the y-intercept is
C. In an exponential growth model y = a. bx, the exponential growth is a and the y-intercept is b. So, the exponential growth is
D. Emma found the x-intercept instead of the y-intercept. The x-intercept is 8,000 and the y-intercept is
and b>

Math
FunctionsWhen the function f(x) is divided by x + 2, the quotient is x² - 5x + 8 and the remainder is 8. Find the function f(x) and write the result in standard form.

Math
FunctionsThe gas mileage for Peter's car is 21 miles per gallon when the car travels at an average speed of 50 miles per hour. The car's gas tank has 17 gallons of gas at the beginning of a trip. If Peter's car travels at an average speed of 50 miles per hour, which of the following functions fmodels the number of gallons of gas remaining in the tank thours after the trip begins?

Math
FunctionsFill out the table of values and select whether each function is odd, even or neither.
For the trig functions, make sure your calculator is in radian mode. You may only
submit once the tables of values have been filled out correctly.
Note: An expression like sinx+ 5 should be typed as sin (x) + 5.



Math
FunctionsThe number of teams y remaining in a single elimination tournament can be found using the exponential function y=128(1/2)^x played in the tournament. Complete parts a through d below.
a. Determine whether the function represents exponential growth or decay. Explain.
.

Math
FunctionsEmma says that for f(x) = 8,000(0.95)X, the exponential growth is 0.95 and the y-intercept is 8,000. What is her error?
Choose the correct answer below and fill in the answer box(es) to complete your choice.
A. For f(x) to be an exponential growth model, a>__and b>___Since b = , it should be exponential decay, not growth.
B. In an exponential growth model y = a.bx, the exponential growth r is found using the equation r = 1 - b. So, the exponential growth is.
C. In an exponential growth model y = a bx, the exponential growth is a and the y-intercept is b. So, the exponential growth is__and the y-intercept is__
D. Emma found the x-intercept instead of the y-intercept. The x-intercept is 8,000 and the y-intercept is__

Math
FunctionsIf you horizontally shift the absolute value parent function, F(x) = Ixl, right nine units, what is the equation of the new function?
A. G(x)= |x |+9
B. G(x)= |x +9|
C. G(x) = |x|-9
D. G(x) = Ix-9|