Permutations and Combinations Questions and Answers
Math
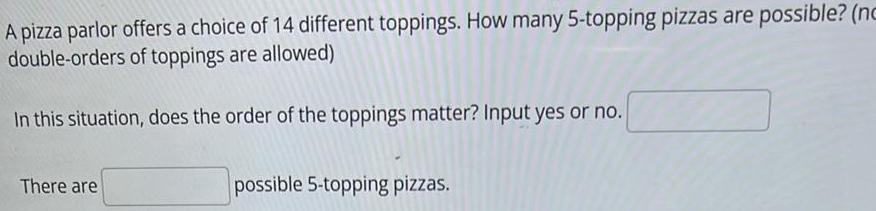
Permutations and CombinationsA pizza parlor offers a choice of 14 different toppings. How many 5-topping pizzas are possible? (nc
double-orders of toppings are allowed)
In this situation, does the order of the toppings matter? Input yes or no.
There are
possible 5-topping pizzas.

Math
Permutations and CombinationsA computer password is required to be 5 characters long. How many passwords are possible if the
password requires 1 letter(s) followed by 4 digits (numbers 0-9), where no repetition of any letter or
digit is allowed?
There are
possible passwords.
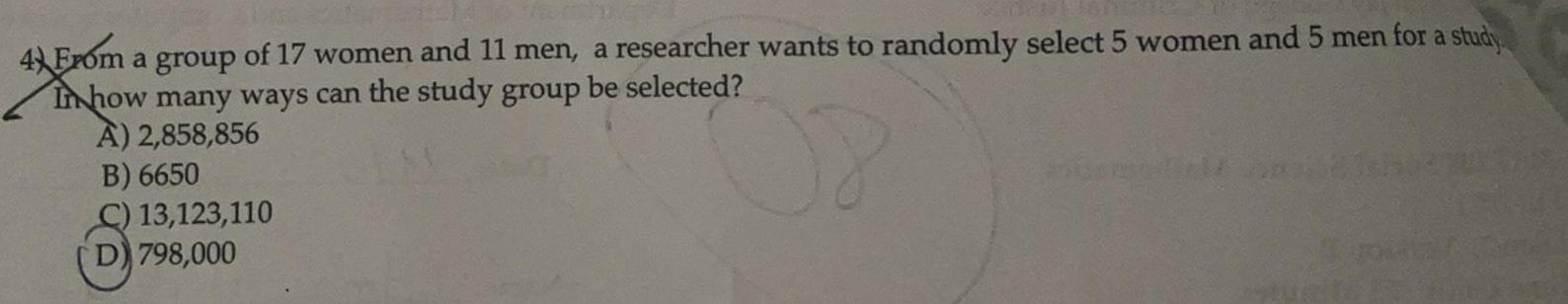
Math
Permutations and CombinationsFrom a group of 17 women and 11 men, a researcher wants to randomly select 5 women and 5 men for a study. In how many ways can the study group be selected?
A) 2,858,856
B) 6650
13,123,110
D) 798,000
Math
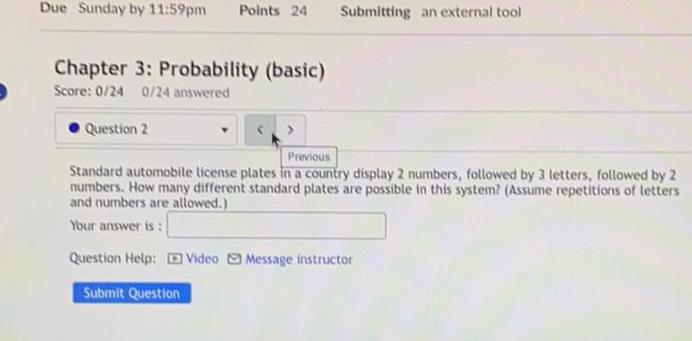
Permutations and CombinationsStandard automobile license plates in a country display 2 numbers, followed by 3 letters, followed by 2
numbers. How many different standard plates are possible in this system? (Assume repetitions of letters
and numbers are allowed.)
Your answer is:

Math
Permutations and Combinations1)
COCA COLA DIRECTORS - THERE ARE 11 MEMBERS ON THE BOARD OF DIRECTORS FOR
THE COCA COLA COMPANY.
MUST ELE
SON, FIRST VICE CHAIRPERSON, SECONDIV
PERSON, AND SECREARY, HOW MANY DIFFERENT SLATES OF CANDID
POSIBELT
B) IF THEY MUST FORM AN ETHICS SUBCOMMITTEE OF FOUR MEMBERS, HOW MANY
DIFFERENT SUBCOMMITTEES ARE POSSIBLE?

Math
Permutations and CombinationsEditors review story ideas and decide what material will appeal most to readers. Editors evaluate submissions from writers to decide what to publish. They also typically allocate space for the text, photos, and illustrations that make up a story. A local newspaper is planning a 7-part series of articles on gun control. The editor has received 15 submissions from his writers. He must decide which articles to publish and the sequence in which to publish them. How many different options are there for the editor to consider?

Math
Permutations and CombinationsWhich of the following is true regarding the sample size when estimating a population mean or proportion?
The larger the sample size the more likely it is to over or underestimate the population mean or proportion.
The size of the sample does not matter as long as it is a simple random sample.
The larger the sample size the more accurate the estimate will be.
The smaller the sample size the more accurate the estimate will be.

Math
Permutations and CombinationsSuppose a designer has a palette of 9 colors to work with, and wants to design a flag with 2 vertical stripes, all of different colors.
How many possible flags can be created?

Math
Permutations and CombinationsIf you toss 5 fair coins, in how many ways can you obtain at least two heads? ("At least two" is the complement of "zero or one.")

Math
Permutations and CombinationsSteve wants to download a selection of new music. How many ways can Steve select three rock songs, two alternative songs, and six rap songs from a list of twelve rock songs, six alternative songs, and eleven rap songs? There are ways that Steve can select his songs.

Math
Permutations and CombinationsFind the value of 12!
239,500,800
39,916,800
479,001,600
6,227,020,800

Math
Permutations and CombinationsAfter meeting with clients to determine the scope of a project, graphic artists typically design layouts and select colors, images, and typeface to use. They then present design concepts to the clients and incorporate changes recommended by clients into final designs. When a graphic designer met with his client, the client approved 5 possible color schemes, 7 possible images, and 4 possible typefaces to be used in the design concept. How many options for the design concept does the graphic artist have if he is choosing one color scheme, one image, and one typeface for the design concept?

Math
Permutations and CombinationsAn access code consists of 1 letter of the alphabet followed by 4 digits. (Digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.) How many different access codes are possible?
Math
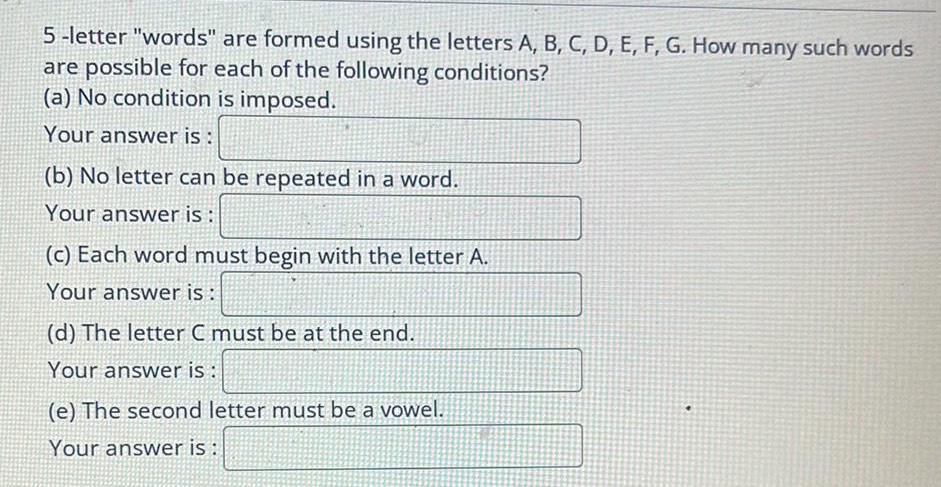
Permutations and Combinationsletter "words" are formed using the letters A, B, C, D, E, F, G. How many such words
are possible for each of the following conditions?
(a) No condition is imposed.
Your answer is:
(b) No letter can be repeated in a word.
Your answer is:
(c) Each word must begin with the letter A.
Your answer is:
(d) The letter C must be at the end.
Your answer is :
(e) The second letter must be a vowel.
Your answer is:

Math
Permutations and CombinationsSWIMMING EVENT - A SWIMMING MEET HAS 15 PARTICIPANTS FOR THE 100 METER
FREESTYLE EVENT. THE 6 PARTICIPANTS WITH THE FASTEST SPEED WILL BE LISTED IN
THE ORDER OF THEIR SPEED ON THE TOTE BOARD. HOW MANY DIFFERENT WAYS ARE
THERE FOR THE NAMES TO BE LISTED?

Math
Permutations and CombinationsThere are 18 finalists in a singing competition. The top five singers receive prizes. How many ways can the singers finish first through fifth?
Math
Permutations and CombinationsYou are conducting a study to see if the average male life expectancy is significantly different from 96. Your sample data (n places. = 20) produce the test statistic t = 3.16. Find the p-value accurate to 4 decimal
Math
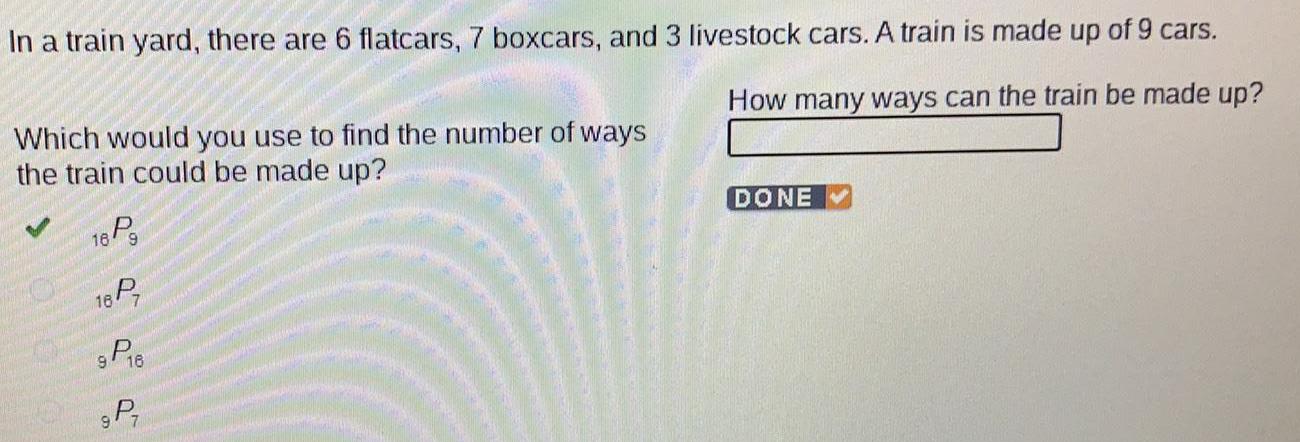
Permutations and CombinationsIn a train yard, there are 6 flatcars, 7 boxcars, and 3 livestock cars. A train is made up of 9 cars.
How many ways can the train be made up?
Which would you use to find the number of ways the train could be made up?

Math
Permutations and CombinationsA small regional carrier accepted 11 reservations for a particular flight with 10 seats. 5 reservations
went to regular customers who will arrive for the flight. Each of the remaining passengers will arrive
for the flight with a 59% chance, independently of each other.
(Report answers accurate to 4 decimal places.)
Find the probability that overbooking occurs.
Find the probability that the flight has empty seats.

Math
Permutations and CombinationsA skiing event has 12 participants for the slalom. The 6 participants with the fastest speeds will be listed, in the order of their speed, on the leader board. How many different ways are there for the names to be listed?

Math
Permutations and CombinationsProblem 1. Consider a set S of nk balls, each of which has one of n distinct colors and one of n distinct diameters. Furthermore, there are exactly k balls of each color and exactly k balls of each diameter. Show that n balls can be selected such that every diameter and color appears in the final selection.

Math
Permutations and CombinationsA random sample of 864 births in a state included 428 boys. Construct a 95% confidence interval estimate of the proportion of boys in all births. It is believed that among all births, the proportion of boys is 0.506. Do these sample results provide strong evidence against that belief?

Math
Permutations and CombinationsA random sample of 863 births in a state included 427 boys. Construct a 95% confidence interval estimate of the proportion of boys in all births. It is believed that among all births, the proportion of boys is 0.509. Do these sample results provide strong evidence against that belief?

Math
Permutations and CombinationsAva is a computer technician. One day, she drove 178 mi away from Newark for a service call. The next day, she drove 81 1/8 mi back toward Newark for another. service call. How far was she then from Newark?
Ava was miles away from Newark
(Simplify your answer. Type a mixed numeral, if possible. Otherwise, type a whole number or a fraction)

Math
Permutations and CombinationsIf Pasha throws a fair 12 sided die (numbered from 1 to 12), and then Sasha throws a fair 8 sided die (numbered from 1 to 8), what is the probability their dice show the same number? Write your answer as a fraction in simplest form.

Math
Permutations and Combinations'A' is a set containing n elements. A subset 'P' of 'A' is chosen. The set 'A' is reconstructed by
replacing the elements of 'P', A subset 'Q' of 'A' is again chosen. The number of ways of choosing
'P' and 'Q', so that PnQ contains exactly two elements is
A
B
D
9¹C₂
3- "C₂
2¹C₁
none of these

Math
Permutations and CombinationsMelissa is arranging 13 cans of food in a row on a shelf. She has 4 cans of corn, 1 can of beans, and 8 cans of carrots. In how many distinct orders can the cans be arranged if two cans of the same food are considered identical (not distinct)?
Math
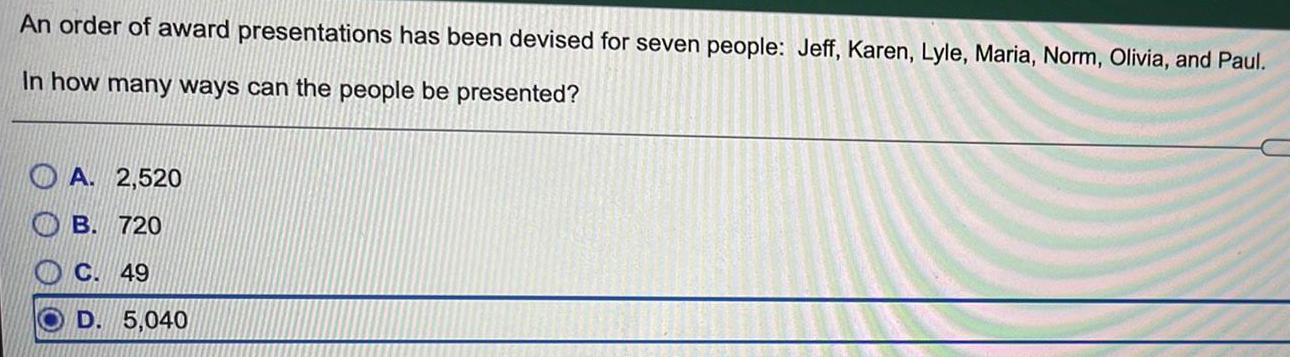
Permutations and CombinationsAn order of award presentations has been devised for seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul. In how many ways can the people be presented?
A. 2,520
B. 720
C. 49
D. 5,040

Math
Permutations and CombinationsA group consists of four men and six women. Three people are selected to attend a conference.
a. In how many ways can three people be selected from this group of ten?
b. In how many ways can three women be selected from the six women?
c. Find the probability that the selected group will consist of all women.

Math
Permutations and CombinationsIn how many ways can 11 people be chosen and arranged in a straight line, if there are 12 people from whom to choose?
A. 479,001,600 ways
B. 132 ways
C. 12 ways
D. 24 ways

Math
Permutations and CombinationsSuppose we want to choose 2 letters, without replacement, from the 4 letters A, B, C, and D.
(a) How many ways can this be done, if the order of the choices matters?
(b) How many ways can this be done, if the order of the choices does not matter?

Math
Permutations and CombinationsTo use an automated teller machine at a certain bank, you must enter a 6-digit code, using the digits 1-9. How many 6-digit codes are possible if repetition of digits is permitted?
Math
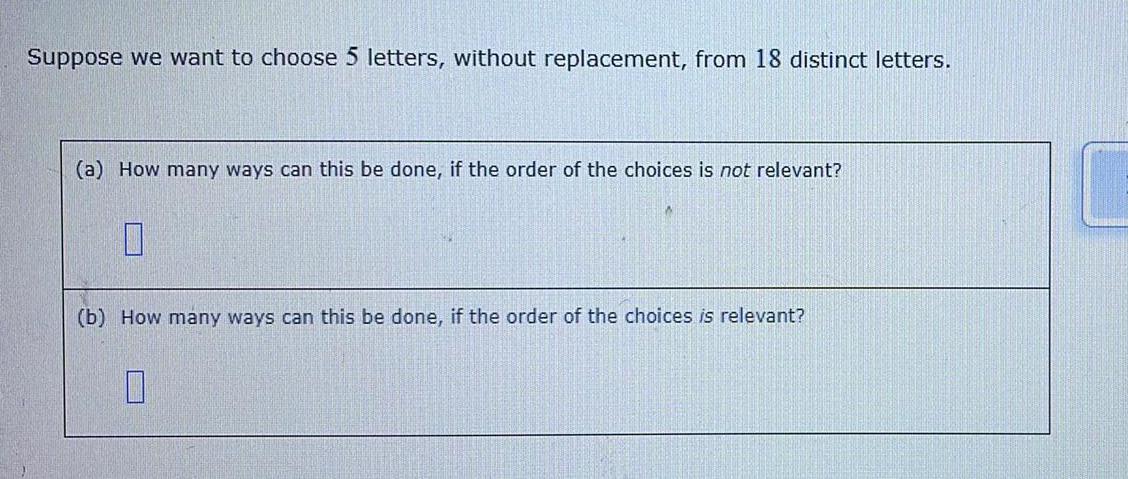
Permutations and CombinationsSuppose we want to choose 5 letters, without replacement, from 18 distinct letters.
(a) How many ways can this be done, if the order of the choices is not relevant?
(b) How many ways can this be done, if the order of the choices is relevant?

Math
Permutations and CombinationsFive different colored flags will be placed on a pole, one beneath another. The arrangement of the colors indicates the message. How many messages are possible if five flags are to be selected from nine different colored flags?

Math
Permutations and CombinationsIf 5 cards are dealt from a standard deck of cards, how many different ways can four face cards and one non-face card be dealt? (A face card is a king, queen, or jack.)
There are five-card hands consisting of four face cards and one non-face card.
(Type a whole number.)

Math
Permutations and CombinationsA pharmaceutical company is going to issue new ID codes to its employees. Each code will have three letters followed by one digit. The letters H and I and the digits 2, 4, 6, and 8 will not be used. So, there are 24 letters and 6 digits that will be used. Assume that the letters can be repeated. How many employee ID codes can be generated?

Math
Permutations and CombinationsSuppose there is a list of nine jokes about books. In how many ways can these nine jokes be ranked from best to worst?

Math
Permutations and CombinationsIn how many ways can a person order one ice cream cone with 3 different flavors of ice cream if there are 9 flavors to choose from and it matters to the person how the 3 flavors are stacked on the one cone? That is, which flavor is on the top, middle, and bottom.

Math
Permutations and CombinationsOf 18 possible books, you plan to take 8 with you on vacation. How many different collections of 8 books can you take?
You can take__ different collections of 8 books on vacation with you.

Math
Permutations and CombinationsHow many different committees can be formed from 9 teachers and 46 students if the committee consists of 3 teachers and 2 students?
The committee of 5 members can be selected in__ different ways.

Math
Permutations and CombinationsSuppose a jar contains 10 red marbles and 17 blue marbles. If you reach in the jar and pull out 2 marbles at random at the same time, find the probability that both are red.

Math
Permutations and CombinationsIn how many ways can a committee of four men and five women be formed from a group of ten men and seven women?

Math
Permutations and CombinationsA signal can be formed by running different colored flags up a pole, one above the other. Find the number of different signals consisting of 7 flags that can be made using 3 white flags, 2 red flags, and 2 blue flags.

Math
Permutations and CombinationsA club with six members is to choose three officers: president, vice-president, and secretary-treasurer. If each office is to be held by one person and no person can hold more than one office, in how many ways can those offices be filled?

Math
Permutations and CombinationsTo win at LOTTO in one state, one must correctly select 7 numbers from a collection of 47 numbers (1 through 47). The order in which the selection is made does not matter. How many different selections are possible? There are different LOTTO selections.

Math
Permutations and CombinationsIn an encyclopedia of language, the author presents five sentences that make a reasonable paragraph regardless of their order. The sentences are listed below.
Mark had told him about the foxes.
John looked out of the window.
Could it be a fox?
However, nobody had seen one for months.
He thought he saw a shape in the bushes.
In how many different orders can the five sentences be arranged?
The five sentences can be arranged in different orders.

Math
Permutations and CombinationsA comedian knows seven jokes, two are about the weather and five are about sports. In how many ways can people select their favorite joke about the weather and their two favorites jokes told about sports?

Math
Permutations and CombinationsIt is presentation day in class and your instructor is drawing names from a hat to determine the order of the presentations. If there are 14 students in the class, what is the probability that the first 4 presentations will be by Harmony, Aaron, Morgan, and Todd, in that order? Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.

Math
Permutations and CombinationsA pizza parlor has three types of crust, 8 different toppings, and two different cheese blends to choose from. In how many ways could you order a three-topping pizza (one type of crust, three different toppings, and one cheese blend)?

Math
Permutations and CombinationsDetermine whether the statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement.
Because the words BET and BEE both contain three letters, the number of permutations of the letter in each word is 3!, or 6.
Choose the correct answer.
OA. True
B.
O C.
O D.
False. Since BEE has two repeating letters, the number of permutations is
3!
2!1!'
False. Since BET has no repeating letters, the number of permutations is
(3-
False. Since BEE has two repeating letters, the number of permutations is
which equals 3.
3!
3-0)!'
1
3!
(3-1)!
which equals 1.
3
which equals 3.