Differentiation Questions and Answers

Math
DifferentiationA constant volume of cookie dough is formed into a cylinder with a relatively small height and large radius When the cookie dough is placed into the oven the height of the doug the radius increases but it retains its cylindrical shape At time t the height of the dough is 10 mm the radius of the dough is 16 mm and the radius of the dough is increasing a per minute Part A At time t at what rate is the area of the circular surface of the cookie dough increasing with respect to time 5 points Part B At time t at what rate is the height of the dough decreasing with respect to time 5 points

Math
DifferentiationStep 1 To determine the intervals on which the function is increasing or decreasing first find the critical numbers of the given function Determine g x g x x 2x 360 g x 2x 2 Step 2 To determine the critical numbers of g x set g x equal to zero and solve for x g x 0 2 x 11 2x 2 0 g 0 g 0 20 g 0 0 Step 3 Since there is no point for which g x does not exist x 1 is the only critical number Thus the number line can be divided into two intervals 1 and 1 Determine the sign of g x at one test value in each of the two intervals X First consider the interval 1 Let x 0 g x 2 x 1 1 2x2 0 1 1 1 Step 4 Since g 0 0 for which interval is the function decreasing Enter your answer using interval notation 0 1 00 1 Step 5 Now consider the interval 1 Let x 2 g x 2 x 1 g 2 2 g 2 2 1

Math
DifferentiationTo test an individual s use of a certain mineral a researcher injects a small amount of a radioactive form of that mineral into the person s bloodstream The mineral remaining in the bloodstream is measured each day for several days Suppose the amount of the mineral remaining in the bloodstream in milligrams per cubic centimeter t days after the initial injection is approximated by C t 2t 3 1 2 Find the rate of change of the mineral level with respect to time for 7 5 days The rate of change of the mineral level with respect to time for 7 5 days is approximately Round to two decimal places as needed milligrams per cubic centimeter per day
Math
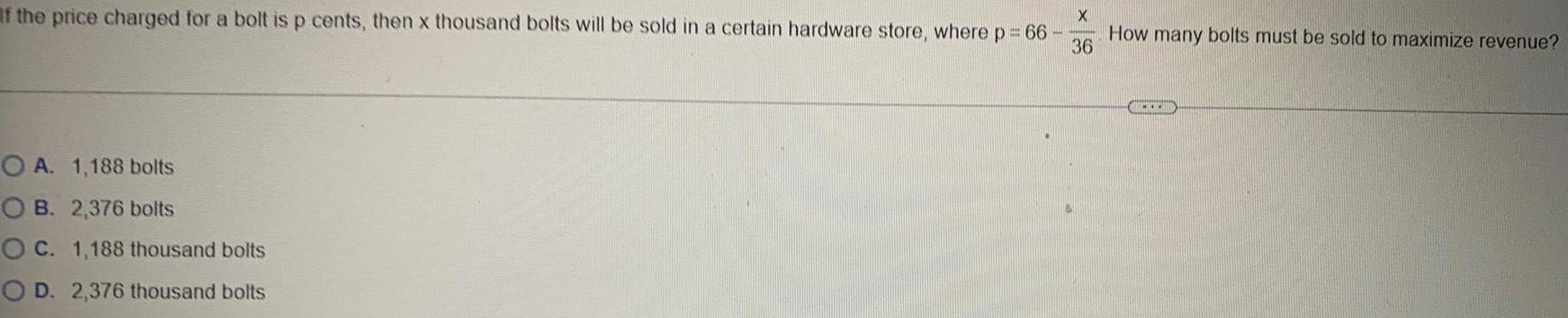
DifferentiationIf the price charged for a bolt is p cents, then x thousand bolts will be sold in a certain hardware store, where p = 66- x/36. How many bolts must be sold to maximize revenue?
A. 1,188 bolts
B. 2,376 bolts
C. 1,188 thousand bolts
D. 2,376 thousand bolts

Math
DifferentiationSuppose that f(4) = 3, g(4) = 4, f'(4) = -5, and g'(4) = 2. Find h'(4).
(a) h(x) = 3f(x) + 2g(x)
h'(4) =
(b) h(x) = f(x)g(x)
h'(4) =
(c) h(x) =f(x)/g(x)
h'(4) =
(d) h(x) =(g(x))/(f(x) + g(x))
h'(4) =

Calculus
DifferentiationThe slope of the line given by the parametric equations x =12t-11 and y = 6t+13 is:
a. 2
b.3
c. 6
d. 1/2
e.1/3

Math
DifferentiationA person standing close to the edge on top of a 80-foot building throws a ball vertically upward. The quadratic function h(t) 16t^,2 +64t+ 80 models the ball's height about the ground, h(t), in feet, t seconds after it was thrown. a) What is the maximum height of the ball? feet b) How many seconds does it take until the ball hits the ground? seconds

Math
DifferentiationLet z₁ and z₂ be two complex numbers satisfying (z-w)²+(z-w²)² = 0, where w is non real cube root of unity. Also let 'a' be a variable point on the circle |z+1/2|=√3/2 and a₁, a2 are values of a such that lal is maximum and minimum respectively.
On the basis of above information, answer the following questions :
Number of complex numbers a such that la - a₁l +|a -a₂l= √6 is
Math
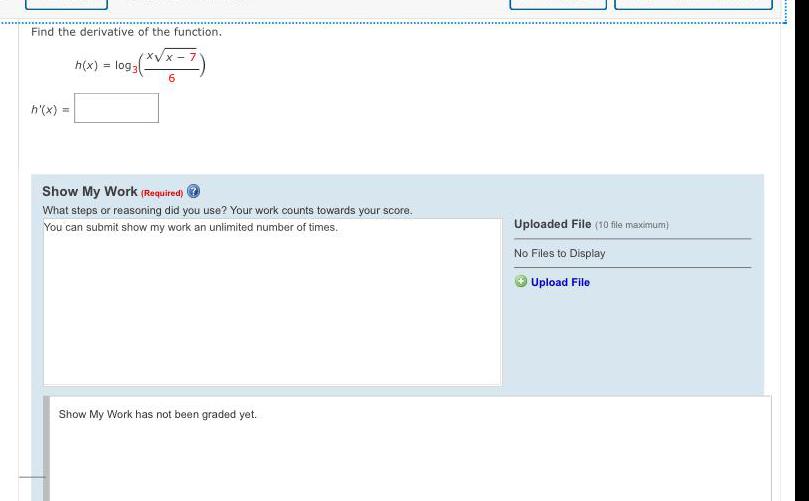
DifferentiationIf f(x) = 2x3/3 - 3x²/2 + 4x, what is f'(x)?
f'(x) = 2x³ - 3x² + 4x
f'(x) = 2x² - 3x + 4
f'(x) = -2x² + 3x - 4
f'(x) = -2x³ + 3x² - 4x
![Use calculus to find the absolute maximum value and the absolute minimum value, if any, of the function. (If an answer does not exist, enter DNE.)
h(x) = ex² - 4 on [-2, 2]
Absolute maximum value: at x = (Enter your answers as a comma-separated list if there are multiple x-values.)
Absolute minimum value: at x = (Enter your answers as a comma-separated list if there are multiple x-values.)](https://media.kunduz.com/media/sug-question/raw/61650169-1659086898.5544593.jpeg?w=256)
Math
DifferentiationUse calculus to find the absolute maximum value and the absolute minimum value, if any, of the function. (If an answer does not exist, enter DNE.)
h(x) = ex² - 4 on [-2, 2]
Absolute maximum value: at x = (Enter your answers as a comma-separated list if there are multiple x-values.)
Absolute minimum value: at x = (Enter your answers as a comma-separated list if there are multiple x-values.)
![Find all values of c that satisfy the mean value theorem for integrals on the following interval
f(x)=√x+9 . [0.4]](https://media.kunduz.com/media/sug-question/raw/56071020-1659004441.9720936.jpeg?w=256)
Math
DifferentiationFind all values of c that satisfy the mean value theorem for integrals on the following interval
f(x)=√x+9 . [0.4]
![On the left-hand side, for the first term 9x³, we have the following.
d/dx[9x³]=_
Now, note that the second term x2y is a product, so we must use the product rule. We therefore have the following.
d/dx[x²y] = (x²)(y') + __](https://media.kunduz.com/media/sug-question/raw/55752619-1659003653.3623345.jpeg?w=256)
Math
DifferentiationOn the left-hand side, for the first term 9x³, we have the following.
d/dx[9x³]=_
Now, note that the second term x2y is a product, so we must use the product rule. We therefore have the following.
d/dx[x²y] = (x²)(y') + __
Math
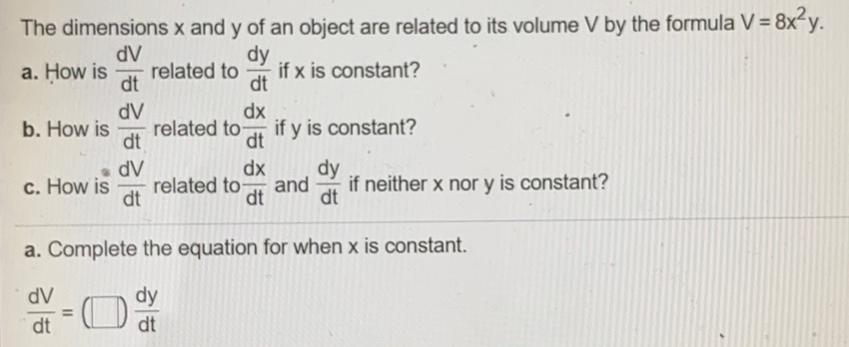
DifferentiationThe dimensions x and y of an object are related to its volume V by the formula V = 8x²y.
a. How is dV/dt related to dy/dt if x is constant?
b. How is dV/dt related to dx/dt if y is constant?
c. How is dV/dt related to dx/dt and dy/dt if neither x nor y is constant?

Math
DifferentiationGiven f(x)= x³-12x+5, find all local maxima and local minima.
B) local max:21, local min: - 11
A) local max: - 11, local min: - 21
D) local max: 11, local min:21
C) local max: -21, local min:11
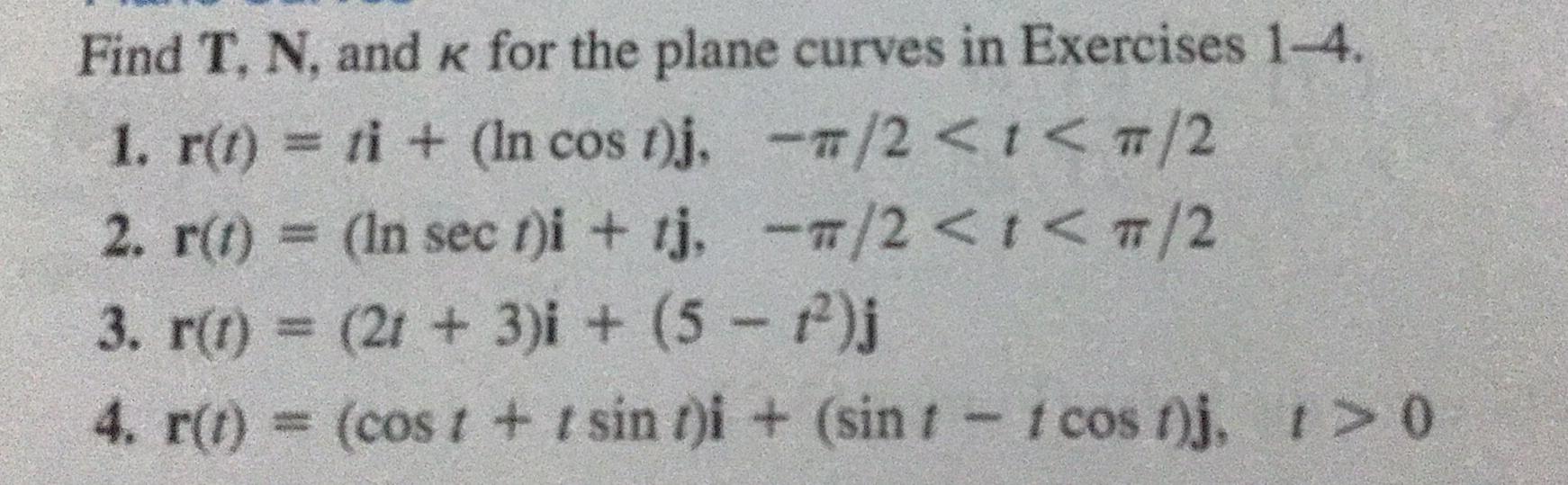
Math
DifferentiationFind T, N, and K for the plane curves in Exercises 1-4.
1. r(t) = ti + (In cos t)j,-π/2 < t< π/2
2. r(t) = (In sect)i + tj,-π/2 < t< π/2
3. r(t) = (2t+ 3)i + (5 −t²)j
4. r(t) = (cost + t sin t)i + (sin 1 - 1 cost)j, t> 0

Math
DifferentiationJenae tosses a quarter from the shore into the St. Johns River. The distance h(t), in feet, from which the quarter is above the water is modeled by the expression h(t) = -16t2+64t where t represents time in seconds.
Use this information to answer the question that follows:
When will the quarter reach its maximum height? seconds
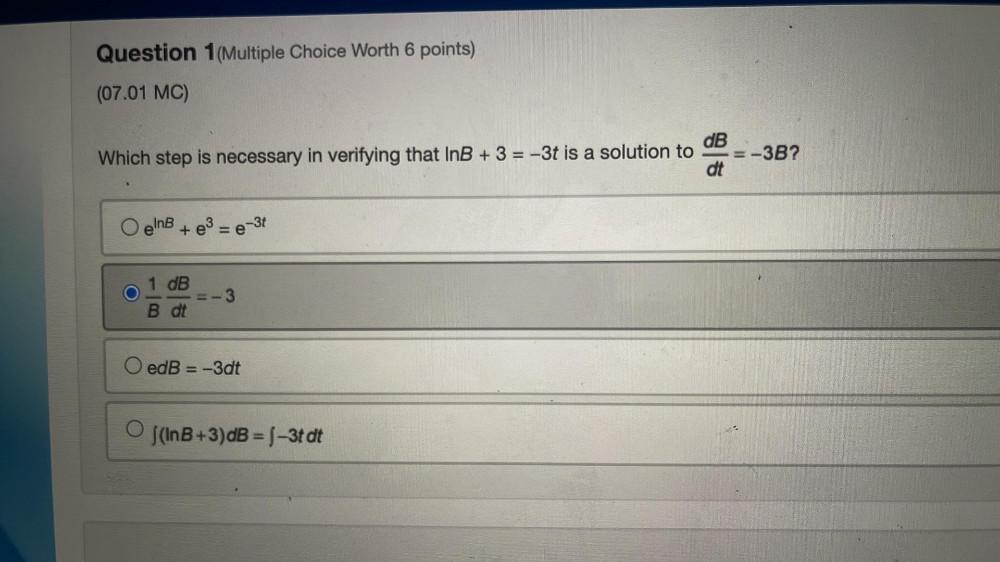
Math
DifferentiationWhich step is necessary in verifying that InB + 3 = -3t is a solution to
dB/dt=-3B?
a)e^InB + e^3 = e^-3t
b)1/B (dB/dt)=-3
c) edB = -3dt
d)∫(InB+3)dB = ∫-3t dt

Math
DifferentiationA ball is thrown into the air from a tree house and eventually lands on the ground. The equation below shows the distance in feet the ball is from the ground seconds after it is thrown. How high will the ball go? Show your work on paper. d(t) = -t^2 +4t +4
![Let f be a twice-differentiable function with derivative given by f'(x) = 4x³ - 24x².
(A) Find the x-coordinate of any possible critical points of f. Show your work.
(B) Find the x-coordinate of any possible inflection points of f. Show your work.
(C) Use the Second Derivative Test to determine any relative extrema and inflection points. Justify your answers.
(D) If f has only one critical point on the interval [5, 8], what is true about the function f on the interval [5, 8]? Justify your answers.](https://media.kunduz.com/media/sug-question/raw/77435682-1658836111.8369439.jpeg?w=256)
Math
DifferentiationLet f be a twice-differentiable function with derivative given by f'(x) = 4x³ - 24x².
(A) Find the x-coordinate of any possible critical points of f. Show your work.
(B) Find the x-coordinate of any possible inflection points of f. Show your work.
(C) Use the Second Derivative Test to determine any relative extrema and inflection points. Justify your answers.
(D) If f has only one critical point on the interval [5, 8], what is true about the function f on the interval [5, 8]? Justify your answers.

Math
DifferentiationFor the differential equation dy/dx=-( e^-x)-3x^2
A): Find a general solution. Show all your work.
B): Verify the solution. Show all your work.

Math
DifferentiationTo measure the physical properties of cells, a piezoelectric probe is used. The force applied by the probe is compared against how much the cell deforms. If F is the force applied by the probe, and w is the distance it moves into the cell, then the stiffness of the cell can be calculated from the rate of change, dF/dw. Zhang et al. found that if F is measured in μN and w in μm then for a zebrafish embryo:
F = 3 x 10⁻⁴ w³- 4.4 x 10⁻³w² + 3.93w+0.221
Calculate dF/dw for a sample when w= 100μm.

Math
DifferentiationIf the derivative f'(x) is negative, decreasing, concave up
Then the function f(x) is (not all info may be used):
increasing, concave up
decreasing, concave up
decreasing, concave down
increasing, concave down

Math
DifferentiationCenterville is the headquarters of Greedy Cablevision Inc. The cable company is about to expand service to two nearby towns, Springfield and Shelbyville. There needs to be cable connecting Centerville to both towns. The idea is to save on the cost of cable by arranging the cable in a Y-shaped configuation. Centerville is located at (12, 0) in the zy-plane, Springfield is at (0, 5), and Shelbyville is at (0, -5). The cable runs from Centerville to some point (x, 0) on the z-axis where it splits into two branches going to Springfield and Shelbyville. Find the location (x, 0) that will minimize the amount of cable between the 3 towns and compute the amount of cable needed. Justify your answer.
To solve this problem we need to minimize the following function of x:
f(x) = =
We find that f(z) has a critical number at x =
To verify that f(x) has a minimum at this critical number we compute the second derivative f''(z) and find that its value at the critical number is , a positive number.
Thus the minimum length of cable needed is

Math
DifferentiationAn orchard owner has shown that if 25 apple trees are planted in one acre, each tree
yields an average of 500 apples. The yield decreases by 10 apples per tree for each
additional tree that is planted
a) determine an equation that models the total yield
b) complete the square
c) how many trees should be planted for maximum total yield?

Math
DifferentiationThe revenue (in dollars) from the sale of x car seats for infants is given by the following function.
R(x)=56x -0.020x² 0≤x≤2800
(A) Find the average change in revenue if production is changed from 1,000 car seats to 1,050 car seats.
(B) Use the four-step process to find R'(x).
(C) Find the revenue and the instantaneous rate of change of revenue at a production level of 1,000 car seats, and interpret the results.
(A) Find the average change in revenue if production is changed from 1,000 car seats to 1,050 car seats.
15 (Round to one decimal place as needed.)
(B) R'(x) =
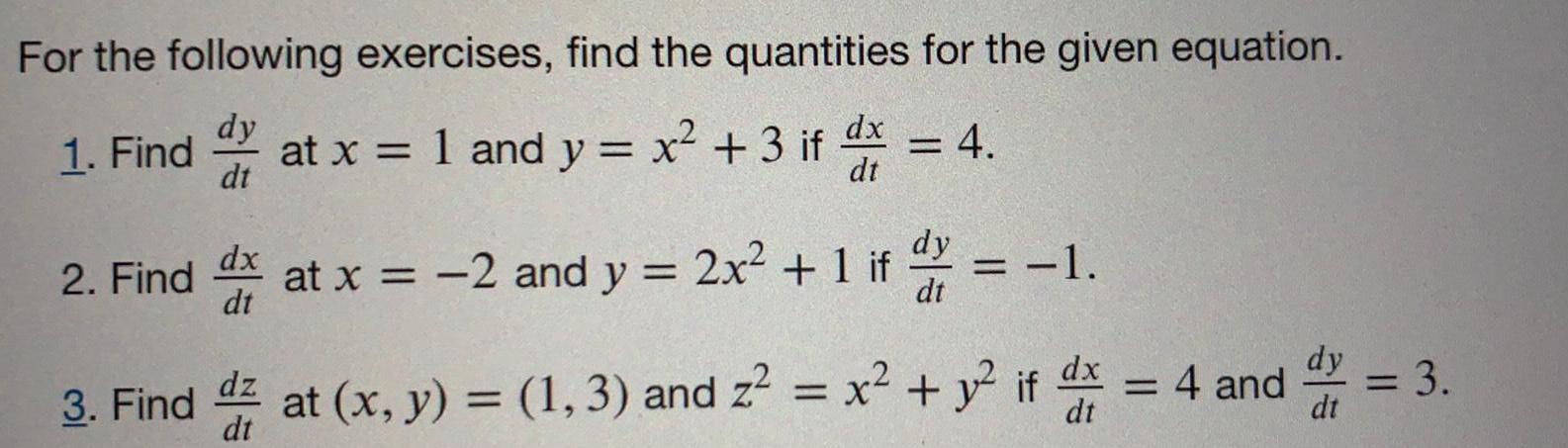
Math
DifferentiationFor the following exercises, find the quantities for the given equation.
1. Find dy/dt at x = 1 and y = x² + 3 if dx/dt = 4
2. Find dx/dt x = -2 and y = 2x² + 1 if dy/dt = -1.
3. Find dx/dt at (x, y) = (1, 3) and z² = x² + y² if dx/dt = 4 and dy/dt= 3.

Math
DifferentiationGiven that 26x⁹ + 5x³⁹ y + y^8
dy/dx
Now find an equation of the line tangent to the graph of 26x9 + 5x³9 y + y = 32 at (1, 1):
![Find f'(x) and simplify.
f(x)= x/x+2
Which of the following shows the correct application of the quotient rule?
A. (x+2)(1)-(x)(1)/ [x+2]²
B. (x)(1)-(x+2)(1)/[x+2]²
C. (x)(1)-(x+2)(1)/[x]²
D. (x+2)(1)-(x)(1)/[x]²](https://media.kunduz.com/media/sug-question/raw/50727628-1658382022.0895762.jpeg?w=256)
Math
DifferentiationFind f'(x) and simplify.
f(x)= x/x+2
Which of the following shows the correct application of the quotient rule?
A. (x+2)(1)-(x)(1)/ [x+2]²
B. (x)(1)-(x+2)(1)/[x+2]²
C. (x)(1)-(x+2)(1)/[x]²
D. (x+2)(1)-(x)(1)/[x]²


Math
DifferentiationFind the difference quotient f(x+h)-f(x)/h where h≠0, for the function below.
f(x)=5x²-6x-7
Simplify your answer as much as possible.

Math
DifferentiationA study was commissioned to find the mean weight of the residents in certain town. The study found the mean weight to be 185 pounds with a margin of error of 6 pounds. Write a confidence interval for the true mean weight of the residents of the town.

Math
DifferentiationYou need to construct a rectangular box with a volume of a volume of 800 cm³ whose base length is three times the base width. The material used to build the top and bottom costs 0.09 per square cm and the material used to build the sides costs 0.12 per square cm. The cost of the least expensive box is: $ (Your written work should include the dimensions of the box.)
![Find a formula for f¹(x) if f(x) =[x+1/ x+1]^3
ƒ-¹(x)=0
(ƒ-¹)'(x) =
Hint: Undo the operations of f(x) from the outside in. Undo the cubed operation first.](https://media.kunduz.com/media/sug-question/raw/48157404-1658336881.244028.jpeg?w=256)
Math
DifferentiationFind a formula for f¹(x) if f(x) =[x+1/ x+1]^3
ƒ-¹(x)=0
(ƒ-¹)'(x) =
Hint: Undo the operations of f(x) from the outside in. Undo the cubed operation first.

Math
DifferentiationGiven the following functions: f(u) = u7/2 and g(z) = x8 +1. Find:
f(g(x)) =
f'(u) =
f'(g(x)) =
g'(x) =
(ƒog)'(x) =
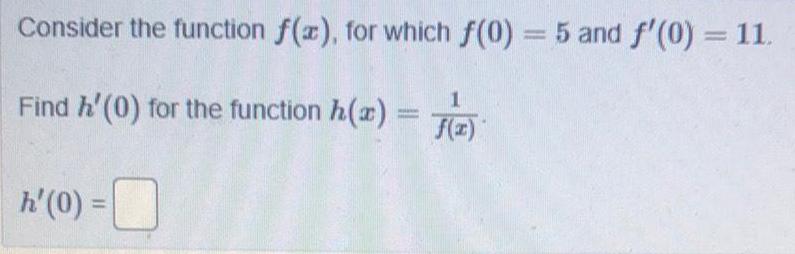
Math
DifferentiationConsider the function f(x), for which f(0) = 5 and f'(0) = 11.
Find h'(0) for the function h(x) = 1/ f(x)
h' (0) =

Math
DifferentiationGiven that f(z) = 2x+cos(x) is one-to-one, use the formula (f ¹)'(x) = 1/ f'(f ¹(x))
to find (f ¹)'(1).
(ƒ˜¹)'(¹) =
![If ƒ(x) = (3x − 4)² (6x² + 6)³ then:
ƒ'(x) =
[Suggestion: use logarithmic differentiation.]](https://media.kunduz.com/media/sug-question/raw/47839054-1658334915.8563726.jpeg?w=256)
Math
DifferentiationIf ƒ(x) = (3x − 4)² (6x² + 6)³ then:
ƒ'(x) =
[Suggestion: use logarithmic differentiation.]

Math
DifferentiationThe slope of the line tangent to the curve 4x² + 3xy + 2y³ = 44 at the point (2, 2) is:

Math
DifferentiationAll you know about a differentiable function f(x) is that:
ƒ'(3) = f'(4) = f'(17) = 0
and that:
f'(x) > 0 for x < 3
f'(x) < 0 for 3 < x < 4
f'(x) < 0 for 4 < x < 17
f'(x) > 0 for 17 < x
Based on this information:
f(x) has
X = 3
f(x) has
X = 4

Math
DifferentiationIf f(x) = x5 · h(x) for some function h(x) and you know that:
h(-3) = -8
h'(-3) = - 5
then f'(-3) =
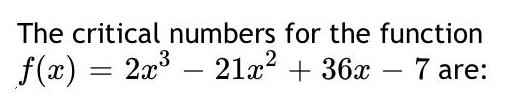


Math
DifferentiationThe circumference of a sphere was measured to be 89 cm
with a possible error of 0.5 cm. Use linear approximation to
estimate the maximum error in the calculated surface area.
Estimate the relative error in the calculated surface area.
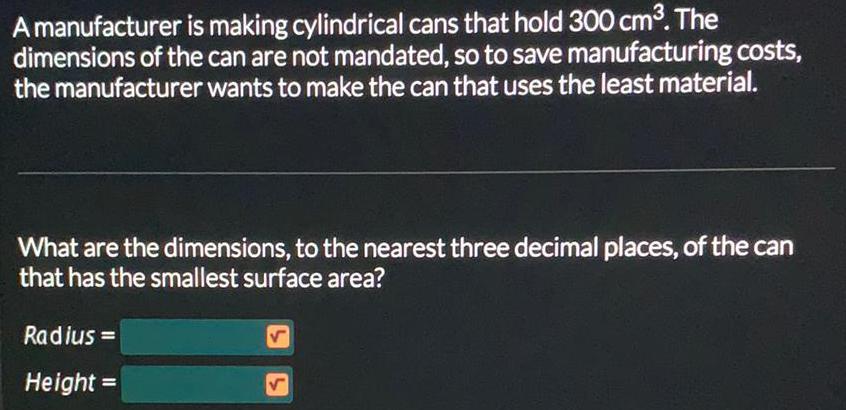
Math
DifferentiationA manufacturer is making cylindrical cans that hold 300 cm³. The
dimensions of the can are not mandated, so to save manufacturing costs,
the manufacturer wants to make the can that uses the least material.
What are the dimensions, to the nearest three decimal places, of the can
that has the smallest surface area?
Radius=
Height =
![Ith (x) = x² + 16x 10 on the interval [-4, 6]:
Apply the mean value theorem to find the value of C in the interval
(-4, 6) such that h' (c) equals the average rate of change of h(x) on
the interval.](https://media.kunduz.com/media/sug-question/raw/45481871-1658260653.3505087.jpeg?w=256)
Math
DifferentiationIth (x) = x² + 16x 10 on the interval [-4, 6]:
Apply the mean value theorem to find the value of C in the interval
(-4, 6) such that h' (c) equals the average rate of change of h(x) on
the interval.

Math
DifferentiationA plane traveled 1120 miles to Cheyenne and back. The trip there was with the wind. It took 10 hours. The trip back was into the wind. The trip back took 20 hours. Find the speed of the plane in still air and the speed of the wind. A) plane: 84 mph, wind: 28 mph C) plane: 39 mph, wind: 39 mph B) plane: 130 mph, wind: 20 mph D) plane: 39 mph, wind: 26 mph

Math
DifferentiationAn arrow is propelled upward. It is s(t) = - 16t² + 80t + 490 feet off the ground after 1 seconds. Find the velocity of the arrow at 3 seconds. Give appropriate units with your answer.
C) 16 ft/s
D) 32 ft/s
A) - 16 ft/s
B) -32 ft/s
![Find all numbers c that satisfy the conclusion of Rolle's Theorem for the following function.
If there are multiple values, separate them with commas; enter N if there are no such values.
f(x) = x² - 4x + 1, [0,4]](https://media.kunduz.com/media/sug-question/raw/43809305-1658253197.974967.jpeg?w=256)
Math
DifferentiationFind all numbers c that satisfy the conclusion of Rolle's Theorem for the following function.
If there are multiple values, separate them with commas; enter N if there are no such values.
f(x) = x² - 4x + 1, [0,4]