Functions Questions and Answers

Math
FunctionsA student records the height of the water in a pool each day for seven days. The function h(t) = |t+2| - 5 models the height of the water h (in feet) in the pool after t days. Find the domain and range for this function and interpret their meaning in the context of the problem.

Math
FunctionsSelect the values that make the inequality c/4>-1 inequality, in terms of c.
(Numbers written in order from least to greatest going across.)

Math
FunctionsIf f(x)=1/x+3 which of the following is true?
I. The domain off is (-∞,-3)U(-3,∞).
II. The graph of f has a vertical asymptote of x = -3.
III. The graph of f has a hole when x = -3.
(A) II only
(B) I and II only
(C) II and III only
(D) I and III only
(E) I, II, and III
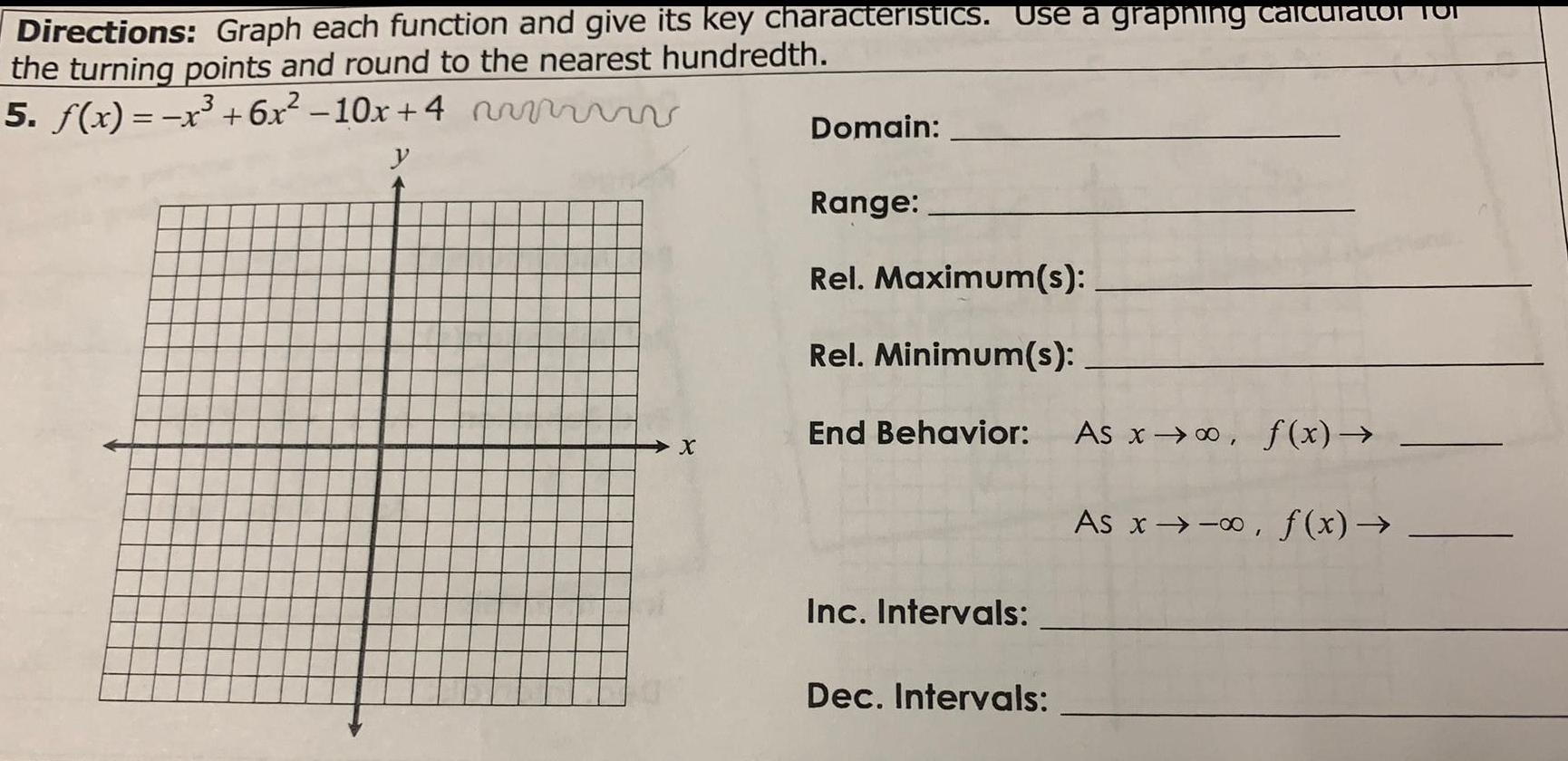
Math
FunctionsDirections: Graph each function and give its key characteristics. Use a graphing calculator for the turning points and round to the nearest hundredth.

Math
FunctionsThe function f is defined as follows.
(a) Find the domain of the function.
(b) Locate any intercepts.
(c) Graph the function.
(d) Based on the graph, find the range.
(a) The domain of the function f is (-∞0,00).
(b) Locate any intercepts. Select the correct choice below and, if necessary, fill in the ans
A. The intercept(s) is/are
B. There are no intercepts.

Math
FunctionsList the interval(s) on which f is increasing. The interval(s) on which f is increasing is/are
(Type your answer in interval notation. Use a comma to separate answers as needed.)

Math
FunctionsThe cost of a Frigbox refrigerator is $875, and depreciates $40 each year. The cost of an Arctic Air refrigerator is $1645, and it depreciates $150 per year.
(a) Find an equation for the value of the Frigbox, F, t years after it is purchased.
F(t) =
(b) Find an equation for the value of the Arctic Air, A, t years after it is purchased.
A(t)
=
(c) If a Frigbox and an Arctic Air are bought at the same time, when do the two refrigerators have equal value? In years.

Math
FunctionsGiven the functions below, find the domain of (fog)(x).
f(x) = -4x - 1
Select the correct answer below:
All real numbers except -and-
and - 10
All real numbers except -
All real numbers except -
and -
All real numbers except -
and-
and -
All real numbers except - and -1
All real numbers except - and -2
g(x) =1
9x +4

Math
FunctionsFill in the blanks.
The function (gof)(x) is found by replacing each occurrence of x in the equation for
The function (gof)(x) is found by replacing each occurrence of x in the equation for
with
with
www.
f(x).
g(f).
g(x).
X.

Math
FunctionsFill in the blanks.
The function (fog)(x) is found by replacing each occurrence of x in the equation for The function (fog)(x) is found by replacing each occurrence of x in the equation for
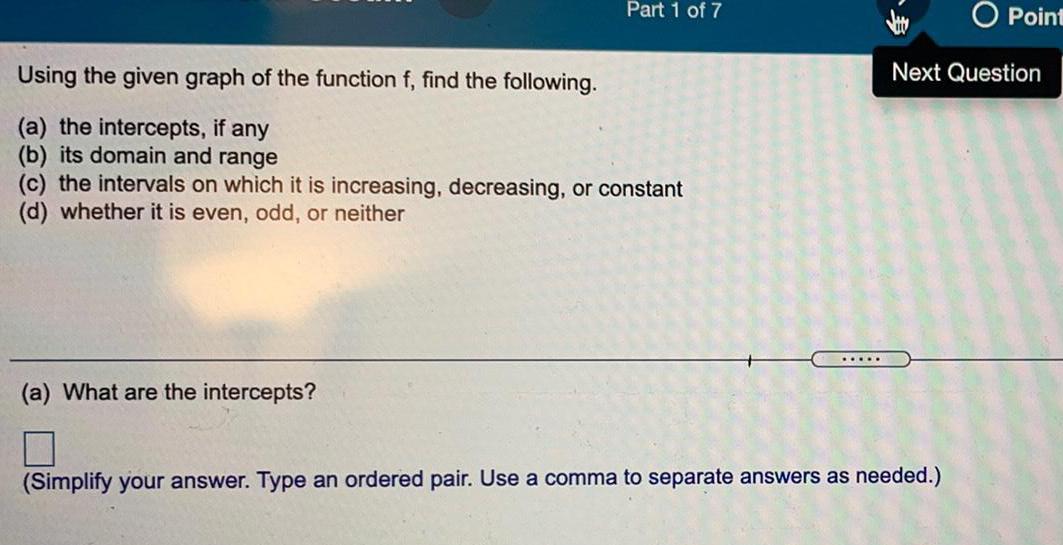
Math
FunctionsUsing the given graph of the function f, find the following.
(a) the intercepts, if any
(b) its domain and range
(c) the intervals on which it is increasing, decreasing, or constant
(d) whether it is even, odd, or neither
(a) What are the intercepts?

Math
FunctionsIn Exercises 8 and 9, construct a table of values of four ordered pairs for the given equation. Check
your results using the table feature of your grapher.
y = x². Start the input variable x at 3, and use an increment of 2.

Math
FunctionsTickets to a Broadway show cost $35 for adults and $10 for children. The total receipts for 1790 tickets at one performance were $47,900.
How many adult and how many child tickets were sold?
Number of Adult tickets sold =
Number of Children tickets sold =


Math
FunctionsAndrea is buying some new shirts and sweaters. She is able to buy 10 shirts and 3 sweaters for $99 or she is able to buy 8 shirts and 7 sweaters for $185. How much does a shirt cost? How much does a sweater cost?
The cost of each shirt
The cost of each sweater =

Math
FunctionsWhich describes the end behavior of the function f(x) = -x⁴+ 4x +37?
Select the correct answer below:
rising to the left and to the right
falling to the left and to the right
rising to the left and falling to the right
falling to the left and rising to the right
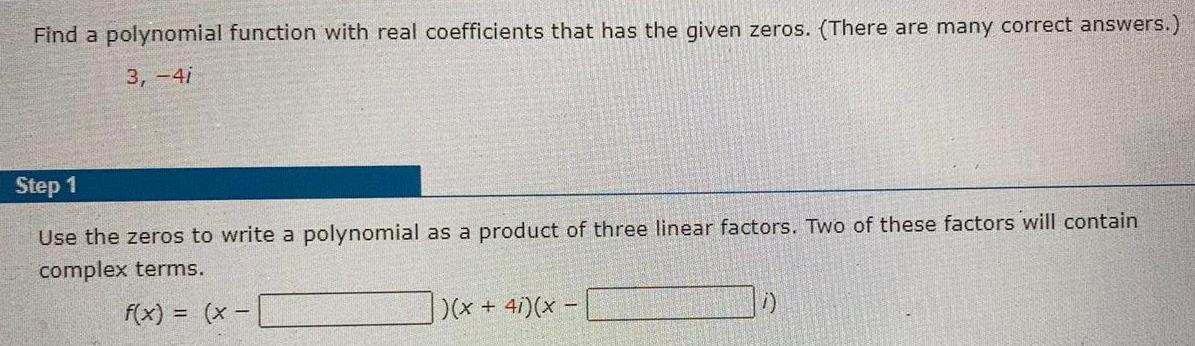
Math
FunctionsFind a polynomial function with real coefficients that has the given zeros. (There are many correct answers.)
3, -4i
Use the zeros to write a polynomial as a product of three linear factors. Two of these factors will contain complex terms.
f(x) = (x - )(x + 4i)(x - i)
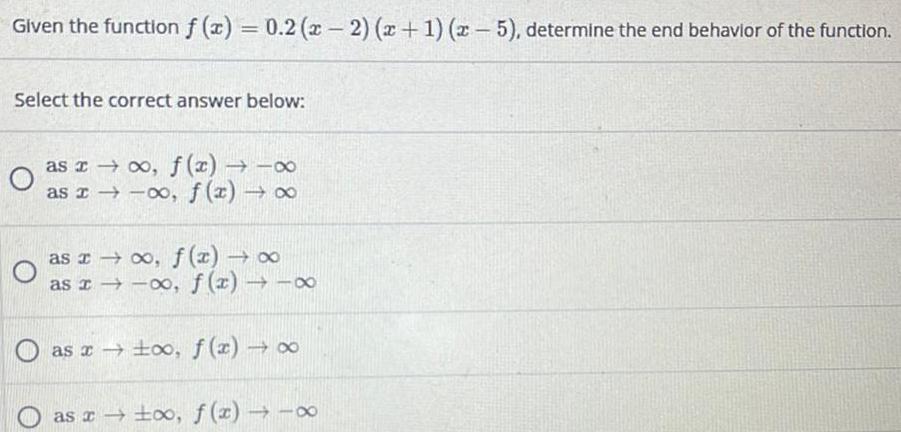
Math
FunctionsGiven the function f(x) = 0.2 (x-2)(x+1) (x - 5), determine the end behavior of the function.
Select the correct answer below:
as x → ∞, f(x) → -∞
as →-∞, f(x) → ∞
as x→ ∞, f(x) → ∞
as x→-∞, f(x) → -∞
as x→ -+∞,f(x) → ∞
as x→ -+∞, f(x) →-∞

Math
FunctionsIf the end behavior is increasing on the left and decreasing on the right, which statement must be true about the function?
Select the correct answer below:
The degree is even and the leading coefficient is positive.
The degree is even and the leading coefficient is negative.
The degree is odd and the leading coefficient is positive.
The degree is odd and the leading coefficient is negative.
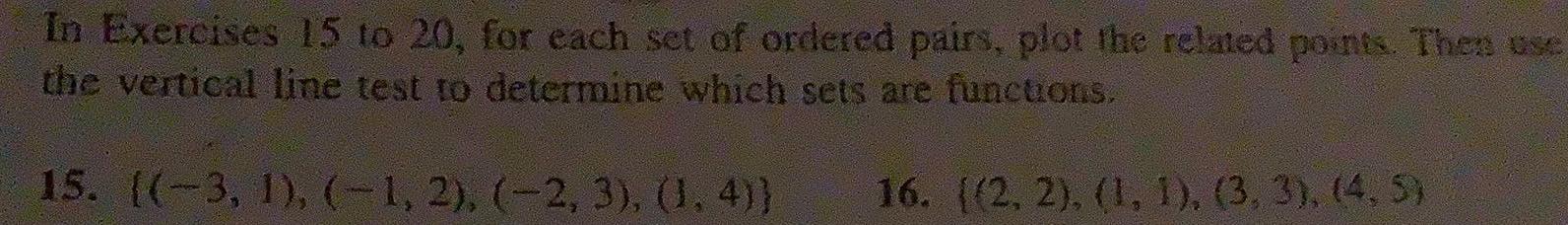
Math
FunctionsIn Exercises 15 to 20, for each set of ordered pairs, plot the related points. Then use
the vertical line test to determine which sets are functions.
15. ((-3, 1), (−1, 2), (2, 3), (1.4)}
16. ((2, 2), (1, 1), (3, 3), (4, 5)

Math
FunctionsWhich of the following sets of data represent valid functions?
G = {(-5, — 3), (1, 3), (1, 4), (7, 8), (11, 10)}
S = {(0, 3), (2, 3), (5, 4), (0, – 3), (12, 11)}
F = {(0, − 1), (2, 3), (5, 6), (7, 9), (14, 11)}
R = {(-3,0), (3, 1), (5, 6), (9, 8), (12, 11)}
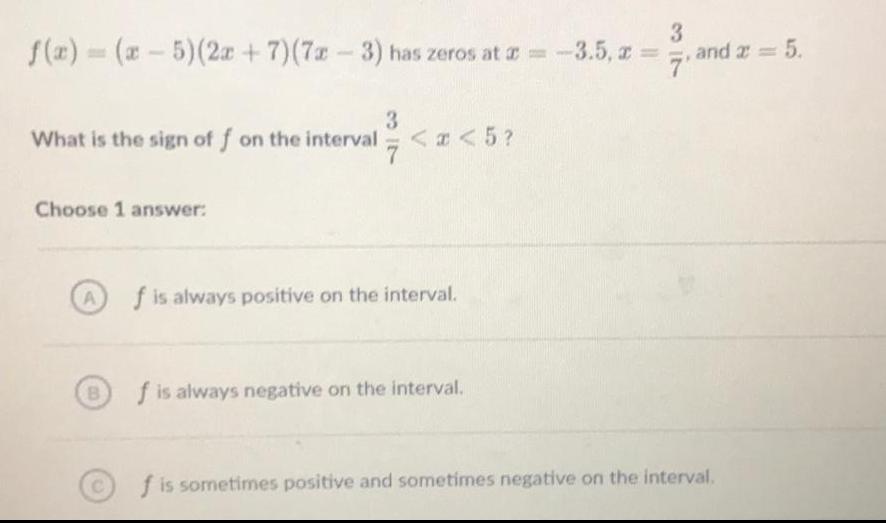
Math
Functionsf(x)=(x - 5)(2x + 7) (7x - 3) has zeros at x = -3.5, x =3/7 , and x = 5.
What is the sign of f on the interval 3/7<x<5?
Choose 1 answer:
A f is always positive on the interval.
B f is always negative on the interval.
C f is sometimes positive and sometimes negative on the interval.

Math
FunctionsThe cost, in dollars, of having n sandwiches delivered is C(n) = 6.5n(n + 5).
(a) Is the function linear?
(b) If the function is linear, give the slope and vertical intercept.
If the function is linear, enter the exact answers. If the function is not linear, enter NA in both answer areas.
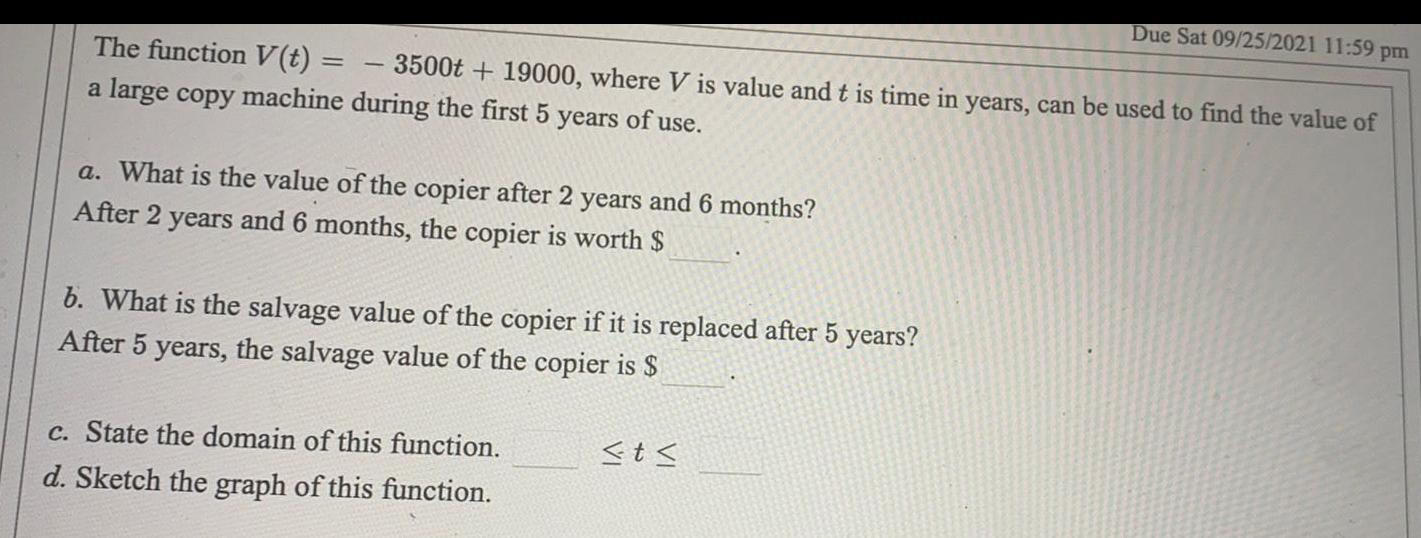
Math
FunctionsThe function V(t) = -3500t + 19000, where V is value and t is time in years, can be used to find the value of a large copy machine during the first 5 years of use.
a. What is the value of the copier after 2 years and 6 months? After 2 years and 6 months, the copier is worth $
b. What is the salvage value of the copier if it is replaced after 5 years? After 5 years, the salvage value of the copier is $
c. State the domain of this function.
d. Sketch the graph of this function.

Math
FunctionsIf the end behavior is decreasing to the left, what might be true about the function? Select all that apply.
Select all that apply:
The degree is even and the leading coefficient is positive.
The degree is even and the leading coefficient is negative.
The degree is odd and the leading coefficient is positive.
The degree is odd and the leading coefficient is negative.
![Find the point of inflection and discuss the concavity of the graph of the function.
f(x) = sin [0, 8π]
Let f be a function whose second derivative exists on a closed open interval I. If f"(x) > 0 for all x in I, then
the graph of f is concave upward
upward on I. And if f"(x) < 0 for all x in I, then the graph of fis downward on I. If a tangent line exists at a point where concavity changes, this
concave downward point is called a point of inflection.
If (c, f(c)) is a point of inflection of the graph of f, then either f"(c) = 0 or f" does not exist at x = c.
Differentiate f(x) with respect to x.](https://media.kunduz.com/media/sug-question/raw/54905688-1658071007.6919742.jpeg?w=256)
Math
FunctionsFind the point of inflection and discuss the concavity of the graph of the function.
f(x) = sin [0, 8π]
Let f be a function whose second derivative exists on a closed open interval I. If f"(x) > 0 for all x in I, then
the graph of f is concave upward
upward on I. And if f"(x) < 0 for all x in I, then the graph of fis downward on I. If a tangent line exists at a point where concavity changes, this
concave downward point is called a point of inflection.
If (c, f(c)) is a point of inflection of the graph of f, then either f"(c) = 0 or f" does not exist at x = c.
Differentiate f(x) with respect to x.
Math
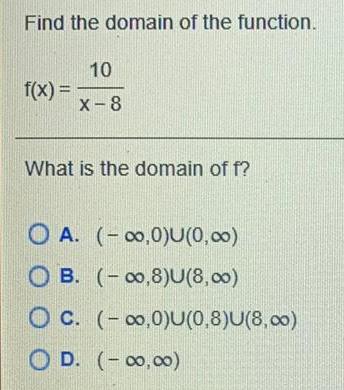
FunctionsFind the domain of the function.
f(x) = 10 / x-8
What is the domain of f?
A. (-∞,0)U(0,∞)
B. (-∞,8)U(8,∞)
C. (-∞,0)U(0,8)U(8,∞)
D. (-∞,∞)

Math
FunctionsIf it takes someone t minutes to drive, run, or walk a mile, then their average speed s(t), in miles per hour, is
given by the formula
Math
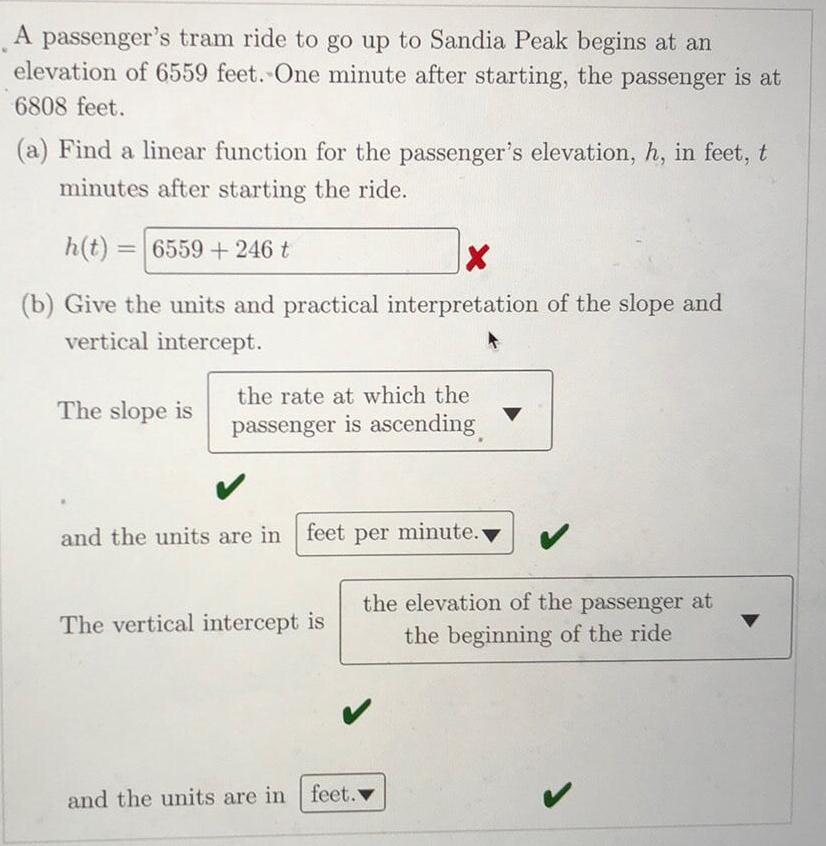
FunctionsA passenger's tram ride to go up to Sandia Peak begins at an elevation of 6559 feet. One minute after starting, the passenger is at 6808 feet.
(a) Find a linear function for the passenger's elevation, h, in feet, t minutes after starting the ride.
h(t) =
(b) Give the units and practical interpretation of the slope and vertical intercept.
The slope is
and the units are in
The vertical intercept is
and the units are in
Math
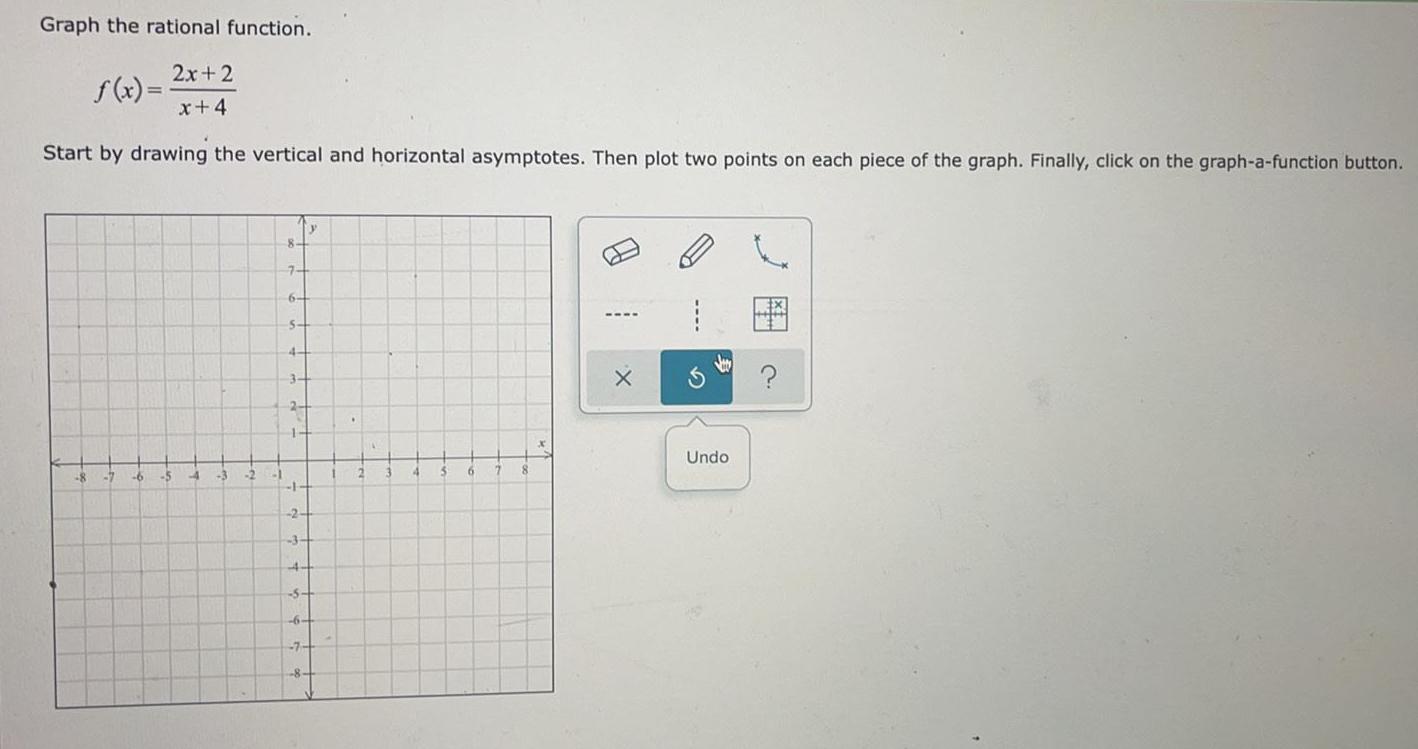
FunctionsGraph the rational function.
f(x)= 2x+2 / x + 4
Start by drawing the vertical and horizontal asymptotes. Then plot two points on each piece of the graph. Finally, click on the graph-a-function button.

Math
FunctionsConsider functions fVand g.
f(x) = log(x - 1)
g(x) = (1/3)x² - 4
Which statement is true about the solutions of the equation f(x) = g(x)?
A. The solutions are where the graphs of the functions intersect at x ≈ -3.464 and x≈ 3.464.
B. The solutions are where the graphs of the functions intersect at x = 1 and x ≈ 3.642.
C. The solutions are where the graphs of the functions cross the x-axis at x ≈ -3.464 and x≈ 3.642.
![Use right and left endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the x-axis over the given interval.
f(x) = 2x + 4, [0, 2], 4 rectangles
To find two approximations of the area of the region between the graph of the function f(x) = 2x + 4 and the x-axis over the interval [0, 2] using 4 rectangles, first partition the interval [0, 2 ] into n = subintervals.
Then the width of each rectangle is given by using the following formula.
Δx = b-a /](https://media.kunduz.com/media/sug-question/raw/54917657-1658068965.848448.jpeg?w=256)
Math
FunctionsUse right and left endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the x-axis over the given interval.
f(x) = 2x + 4, [0, 2], 4 rectangles
To find two approximations of the area of the region between the graph of the function f(x) = 2x + 4 and the x-axis over the interval [0, 2] using 4 rectangles, first partition the interval [0, 2 ] into n = subintervals.
Then the width of each rectangle is given by using the following formula.
Δx = b-a /

Math
FunctionsFind the tangent line approximation T to the graph of f at the given point. Then complete the table. (Round your answer to four
decimal places.)
f(x)=√x, (3, √3)

Math
Functions(a) Factor the numerator and denominator of f(x), find the roots, leading term and asymptotes.
In this problem we will give a graph sketch of f(x) =
(b) For each root and vertical asymptote from part (a), give the degree.
(c) Determine the sign decomposition for f(x) (aka where f(x) is positive and negative).
(d) Graph f(x). Include all roots and asymptotes.

Math
FunctionsFor the function y = x² + 6 there are no such restrictions on the domain. When there are no restrictions, the domain of a function consists of all real numbers because there are no exclusions. The inputs come from all values on the real number line which span from negative infinity to positive infinity.
Enter the domain of the function y = x² + 6 using interval notation.

Math
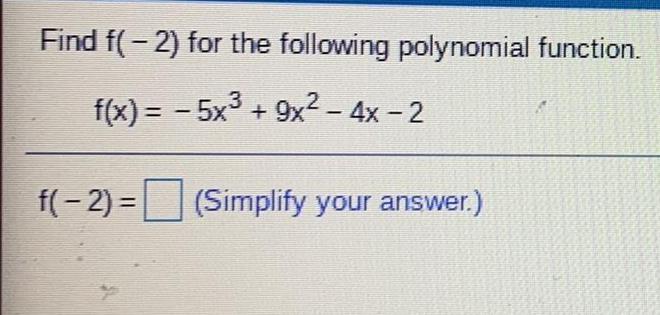
FunctionsState the domain and range of the function. (Enter your answers using interval notation.)
y = x² + 5

Math
Functionsf(x)= x³ - 3x² + 2; horizontal stretch by a factor of 3 and a translation 3 units up, followed by a reflection in the x-axis

Math
FunctionsIn Exercises 10 and 11, write a rule for g that represents the indicated transformations of the graph of f.
21. f(x)=x²-3x² + 2; horizontal stretch by a factor of 3 and a translation 3 units up, followed by a reflection in the x-axis

Math
FunctionsThe one-to-one function h is defined below.
h(x) = 7x / 7-9x
Find h⁻¹(x), where h⁻¹ is the inverse of h.
Also state the domain and range of h⁻¹ in interval notation.

Math
FunctionsAn agency charges $100 per person for a trip to a concert if 40 people travel in a group. But for each person above the 40, the amount charged for each traveler will be reduced by $4. If x represents the number of people above the 40, write the agency's revenue R as a function of x. (Assume that x is greater than zero.)
![An object was removed from a furnace and placed in a room with a constant temperature of 20 degree Celsius. The temperature T (in degrees Celsius) at time h (in hours) can be modeled by: T(h)=20[1+8(2-)] h≥o A) What was the temperature of the object when it was removed from the furnace? Show how you arrived at your answer. B) Eventually, what will be the temperature of the object? Show how you arrived at your answer. Does this answer make sense in the context of the problem? Explain your reasoning.](https://media.kunduz.com/media/sug-question/raw/54809639-1658064232.1372325.jpeg?w=256)
Math
FunctionsAn object was removed from a furnace and placed in a room with a constant temperature of 20 degree Celsius. The temperature T (in degrees Celsius) at time h (in hours) can be modeled by: T(h)=20[1+8(2-)] h≥o A) What was the temperature of the object when it was removed from the furnace? Show how you arrived at your answer. B) Eventually, what will be the temperature of the object? Show how you arrived at your answer. Does this answer make sense in the context of the problem? Explain your reasoning.

Math
FunctionsUse transformations of the graph of f(x) = x² to determine the graph of the given function.
h(x) = -(x-3)²
Select all the transformations that are needed to graph the given function using f(x) = x².
A. Shift the graph 3 units to the right.
B. Shift the graph 3 units up.
C. Stretch the graph vertically by a factor of 3.
D. Shrink the graph vertically by a factor of 3.
E. Shift the graph 3 units to the left.
F. Shift the graph 3 units down.
G. Shrink the graph horizontally by a factor of 3.
H. Reflect the graph about the y-axis.
I. Reflect the graph about the x-axis.
J. Stretch the graph horizontally by a factor of 3.
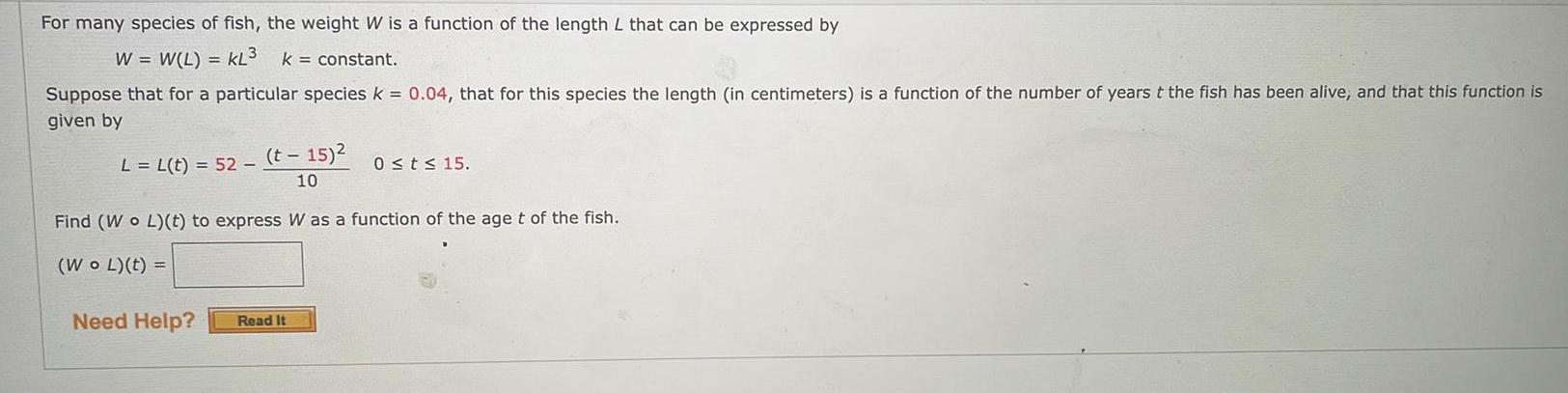
Math
FunctionsFor many species of fish, the weight W is a function of the length L that can be expressed by
Suppose that for a particular species k = 0.04, that for this species the length (in centimeters) is a function of the number of years t the fish has been alive, and that this function is
given by
L = L(t) = 52 (t-15)²
Find (Wo L)(t) to express W as a function of the age t of the fish.
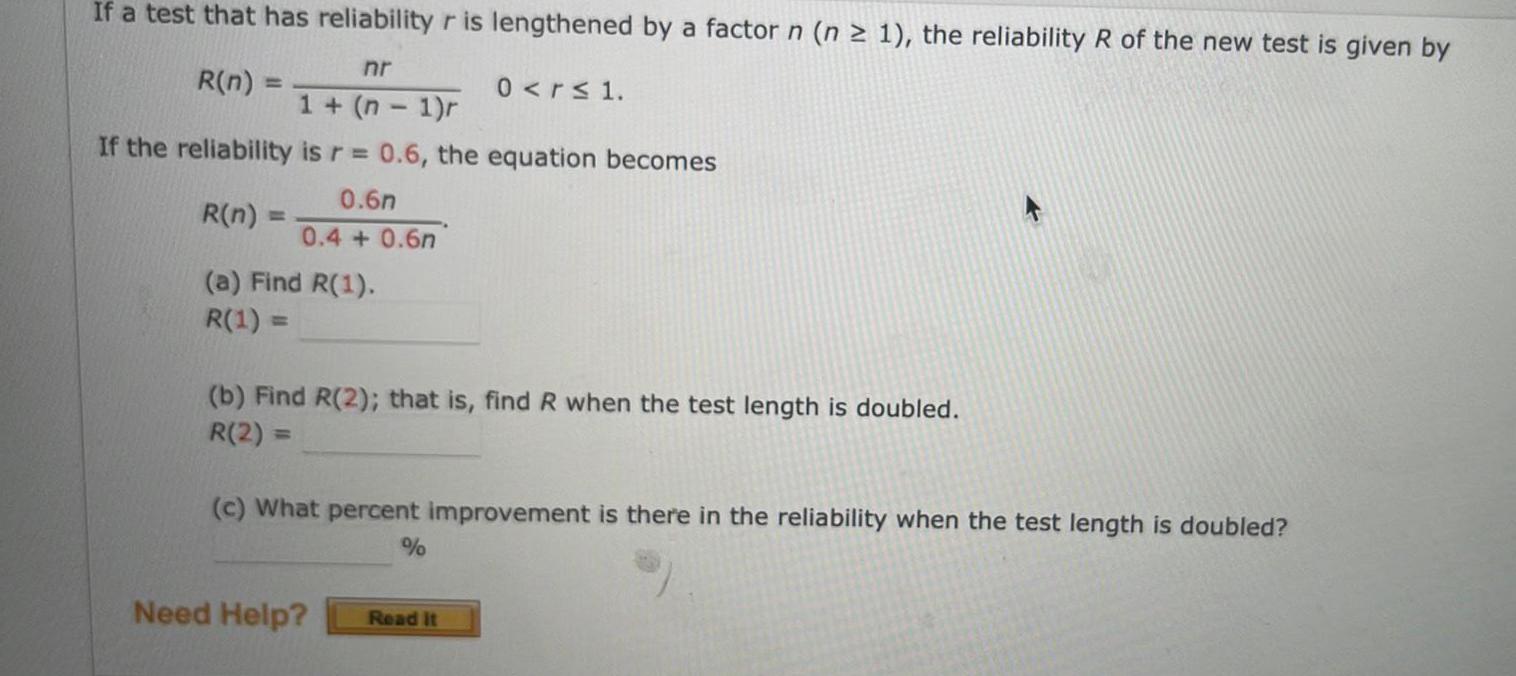
Math
FunctionsIf a test that has reliability r is lengthened by a factor n (n ≥ 1), the reliability R of the new test is given by
If the reliability is r = 0.6, the equation becomes
(b) Find R(2); that is, find R when the test length is doubled.
(c) What percent improvement is there in the reliability when the test length is doubled?

Math
FunctionsSuppose C = f(q) = 125 + 0.05 q is the cost (in dollars) to manufacture q kilograms of a chemical.
a) Find a formula for the inverse of function
ƒ−¹(C) =
b) Which of the following statement(s) correctly explain the meaning of f-¹(C)? Check all that apply.
A. The cost of manufacturing one kilogram of the chemical.
B. The amount (in kilograms) of the chemical that can be manufactured for C dollars.
C. The cost of manufacturing C kilograms of the chemical.
D. The kilogram number of the chemical someone can
purchase with C dollars.
E. The amount of chemical that can be manufactured for one dollar.
F. None of the above

Math
FunctionsUse the values in the following table.
(a) Explain why the table defines y as a function of x.
For some values of y there are multiple values for x.
For each value of x there is only one y.
For each value of y there is only one x.
For each value of x there are multiple values for y.
For each value of y there are multiple values for x.
(b) State the domain and range of this function. (Enter your answers as a comma-separated list.)
(c) If the table expresses y = f(x), find f(0) and f(10). (If the table does not express y =

Math
FunctionsGiven the following function, (a) find the vertex; (b) determine whether there is a maximum or a minimum value, and find the value; (c) find the range; and (d) find the intervals on which the function is increasing and the intervals on which the function is decreasing.
f(x) = - 4x² - 4x + 5
(a) The vertex is
(b) Determine whether the parabola has a maximum value or a minimum value and find the value.
Select the correct choice below and fill in the answer box within your choice.
A. The parabola opens downward and has a maximum value of
B. The parabola opens upward and has a minimum value of
(c) What is the range of f(x)?
The range of f(x) is.
(d) On what interval is the function increasing?
The function is increasing on
On what interval is the function decreasing?
The function is decreasing on.