Functions Questions and Answers
Math
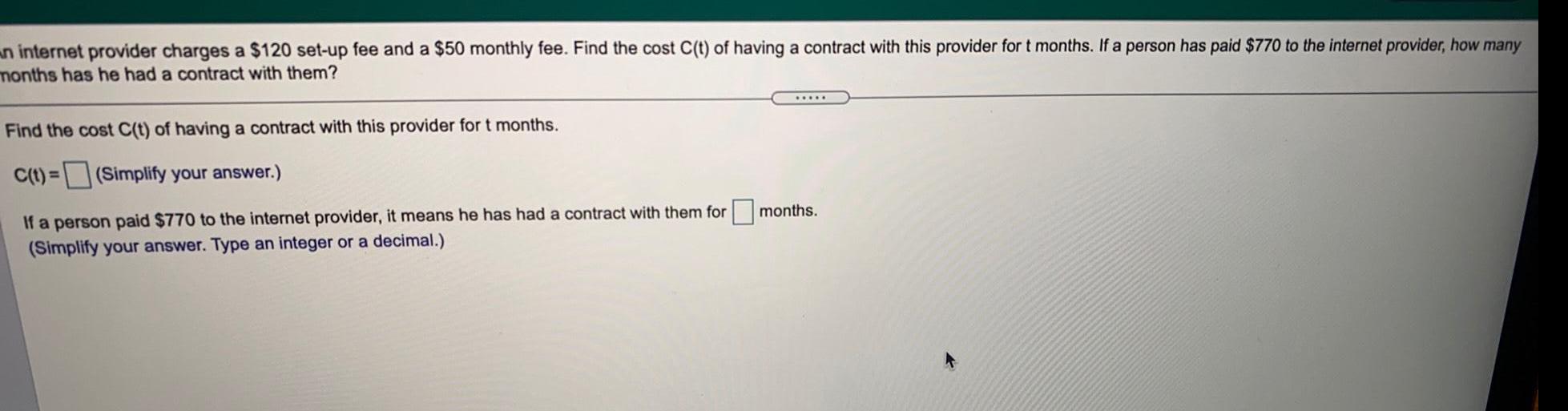
Functionsan internet provider charges a $120 set-up fee and a $50 monthly fee. Find the cost C(t) of having a contract with this provider for t months. If a person has paid $770 to the internet provider, how many
months has he had a contract with them?
*****
Find the cost C(t) of having a contract with this provider for t months.
C(t)=
(Simplify your answer.)
If a person paid $770 to the internet provider, it means he has had a contract with them for months.
(Simplify your answer. Type an integer or a decimal.)
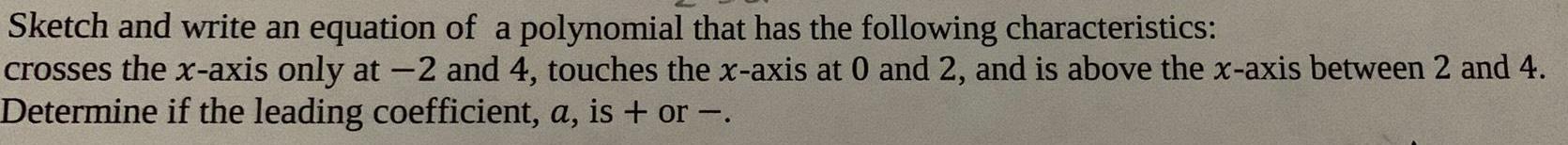
Math
FunctionsSketch and write an equation of a polynomial that has the following characteristics: crosses the x-axis only at -2 and 4, touches the x-axis at 0 and 2, and is above the x-axis between 2 and 4. Determine if the leading coefficient, a, is + or -
Math
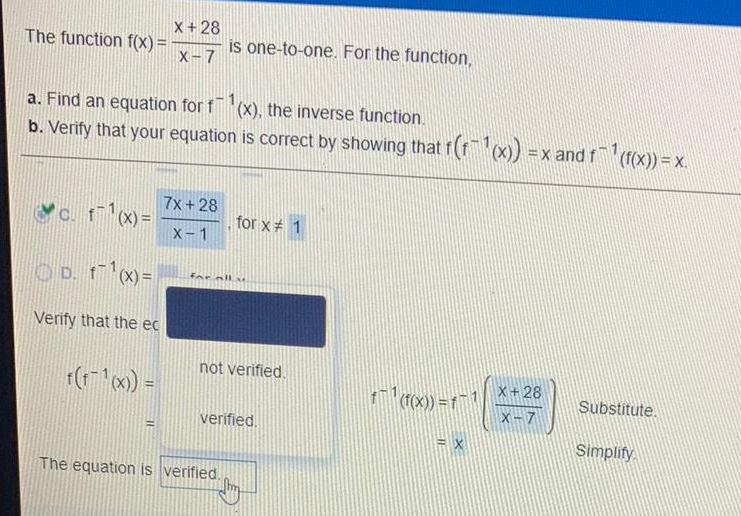
FunctionsThe function f(x) = X+28/X-7
a. Find an equation for f(x), the inverse function.
b. Verify that your equation is correct by showing that f(f(x)) = x and f(f(x)) = x.
D. f (X) =
Verify that the ec is one-to-one. For the function,
far all

Math
FunctionsDetermine the transformations that must be applied to the graph of each function f(x) to obtain the transformed function.
b. Write the transformed equation.
Math
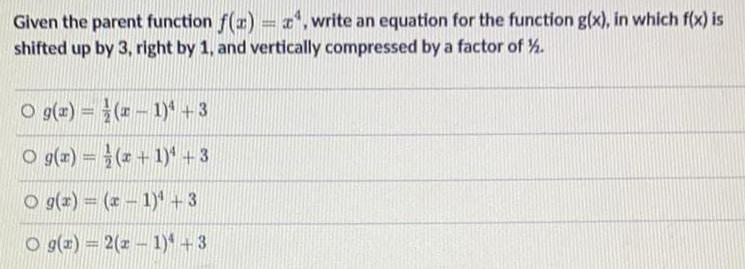
FunctionsGiven the parent function f(x)=x, write an equation for the function g(x), in which f(x) is shifted up by 3, right by 1, and vertically compressed by a factor of %.
g(x) = (2-1) +3
g(x)=(x+1)+3
g(x) = (x - 1)¹ +3
g(x) = 2(x - 1)4+3
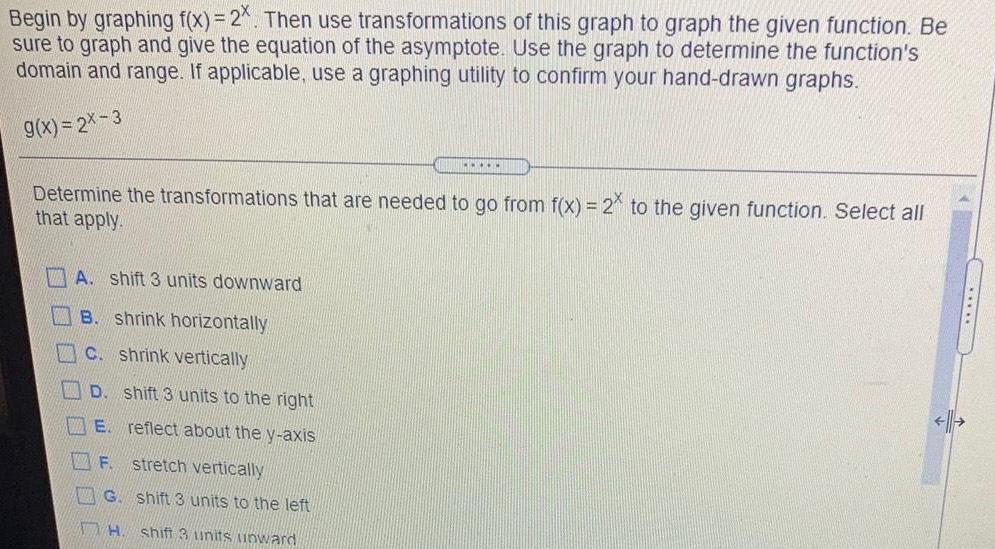
Math
FunctionsBegin by graphing f(x) = 2x. Then use transformations of this graph to graph the given function. Be sure to graph and give the equation of the asymptote. Use the graph to determine the function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x)=2x-3 Determine the transformations that are needed to go from f(x) = 2* to the given function. Select all that apply.
A. shift 3 units downward
B. shrink horizontally
C. shrink vertically
D. shift 3 units to the right
E. reflect about the y-axis
F. stretch vertically
G. shift 3 units to the left
H. shift 3 units upward

Math
FunctionsChoose the end behavior of the graph of each polynomial function.
(a) ƒ(x) = −3x² - 7x²³
(b) f(x) = -5x² + 3x³
(c) f(x) = 3x (x + 1)(x − 4)²
Falls to the left and rises to the right
Rises to the left and falls to the right
Rises to the left and rises to the right
Falls to the left and falls to the right
Falls to the left and rises to the right
Rises to the left and falls to the right
Rises to the left and rises to the right
Falls to the left and falls to the right
Falls to the left and rises to the right
Rises to the left and falls to the right
Rises to the left and rises to the right
Falls to the left and falls to the right
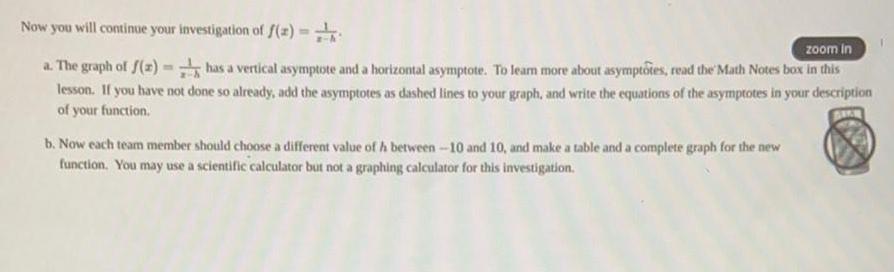
Math
FunctionsNow you will continue your investigation of f(x)=
zoom in
a. The graph of f(z)
has a vertical asymptote and a horizontal asymptote. To learn more about asymptotes, read the Math Notes box in this lesson. If you have not done so already, add the asymptotes as dashed lines to your graph, and write the equations of the asymptotes in your description of your function.
b. Now each team member should choose a different value of h between -10 and 10, and make a table and a complete graph for the new function. You may use a scientific calculator but not a graphing calculator for this investigation.
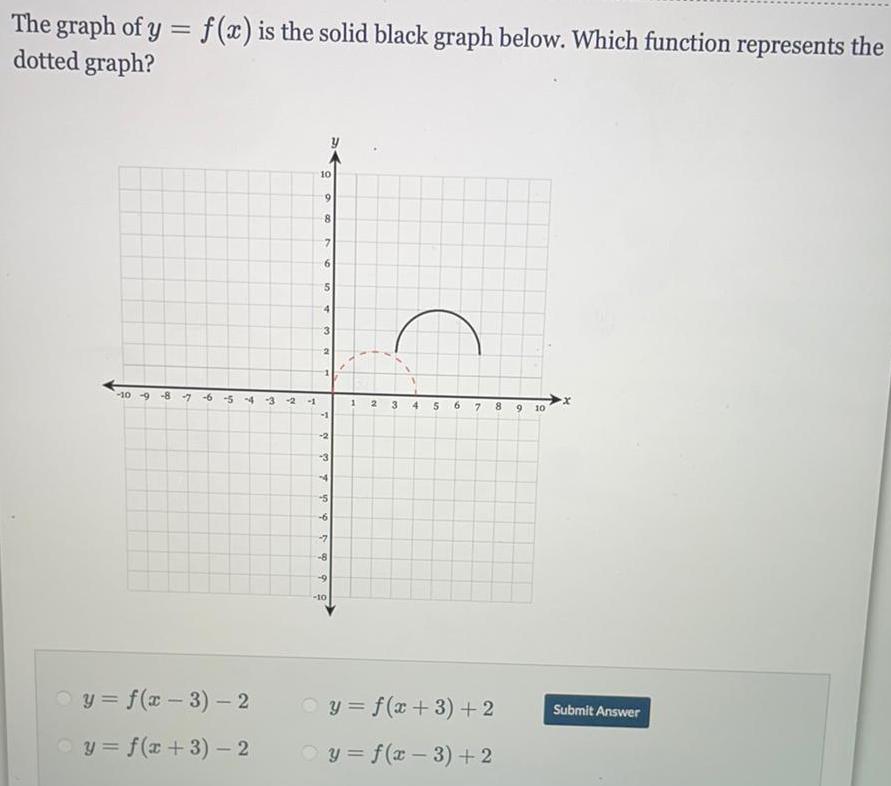
Math
FunctionsThe graph of y = f(x) is the solid black graph below. Which function represents the dotted graph?

Math
FunctionsConsider the following polynomial function.
Answer the questions regarding the graph of f.
Then, use this information to graph the function.
(a) Choose the end behavior of the graph of f.
Falls to the left and rises to the right
(b) List each real zero of faccording to the behavior of the graph at the x-axis near that zero. If there is more than one answer, separate them with commas. If there is no answer, click on "None".
Zero(s) where the graph crosses the x-axis:
Zero(s) where the graph touches, but does not cross the x-axis: 0
(c) Find the y-intercept of the graph of f
(d) Graph f(x)=-x (x-1)(x+1)² by doing the following.
Plot all points where the graph of fintersects the x-axis or y-axis.
For each point on the x-axis, select the correct behavior.

Math
FunctionsAlice, who is paid time-and-a-half for hours worked in excess of 40 hours, had gross weekly wages of $544 for 56 hours worked. What is her regular hourly rate?
Alice's regular hourly rate is per hour.
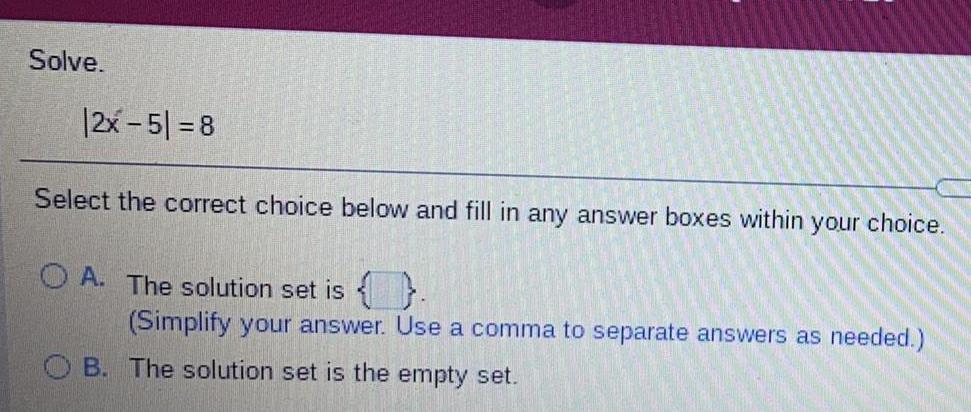
Math
FunctionsSolve.
|2x-5|=8
Select the correct choice below and fill in any answer boxes within your choice.
A. The solution set is {}.
(Simplify your answer. Use a comma to separate answers as needed.)
B. The solution set is the empty set.
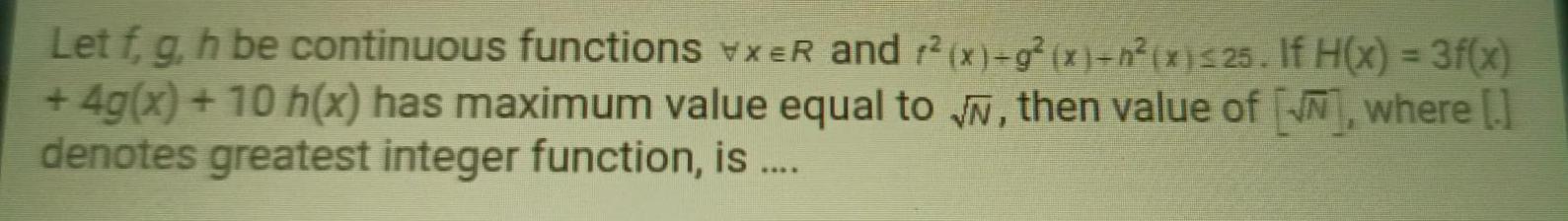
Math
FunctionsLet f, g, h be continuous functions vxER and r²(x)-g² (x)+n²(x) ≤25. If H(x) = 3f(x) +4g(x) + 10 h(x) has maximum value equal to √, then value of , where denotes greatest integer function, is ....

Math
FunctionsThe volume V (r) (in cubic meters) of a spherical balloon with radius r meters is given by V (r)=4/3 πr².
The radius W (t) (in meters) after t seconds is given by W (t)=81+3.
Write a formula for the volume M (t) (in cubic meters) of the balloon after t seconds.
It is not necessary to simplify.

Math
FunctionsDetermine the open intervals on which the graph is concave upward or concave downward. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)
f(x) = x² - 4x + 6
concave upward
concave downward
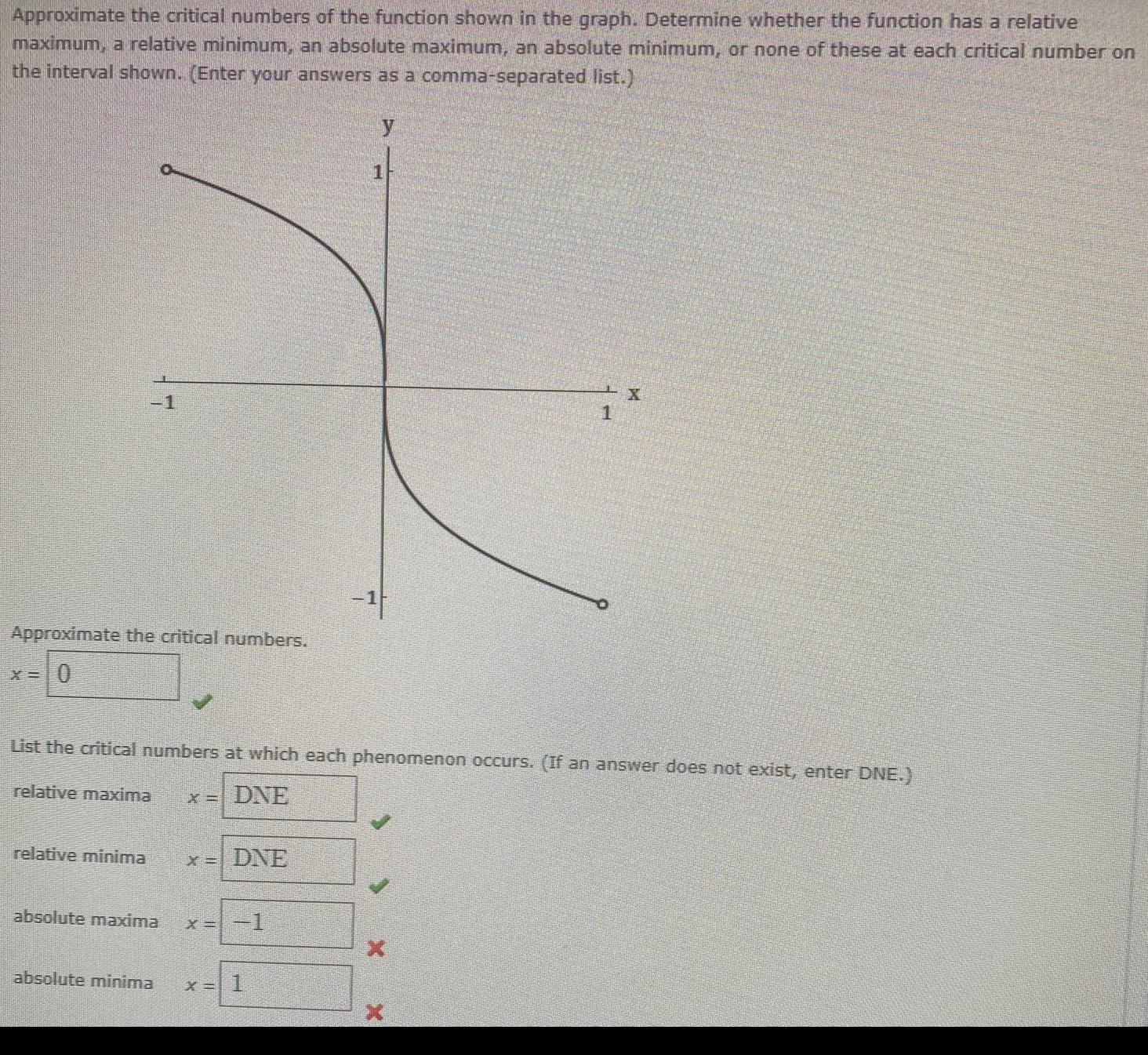
Math
FunctionsApproximate the critical numbers of the function shown in the graph. Determine whether the function has a relative
maximum, a relative minimum, an absolute maximum, an absolute minimum, or none of these at each critical number on the interval shown. (Enter your answers as a comma-separated list.)

Math
FunctionsFind all relative extrema of the function. Use the Second-Derivative Test when applicable. (If an answer does not exist, enter DNE.)
f(x) = x4 4x³ + 5

Math
FunctionsThe function E(x)=0.0031x³ +0.0046x² +0.164x+1.9 gives the approximate total earnings of a company, in millions of dollars, where x = 0 corresponds to 1996, x= 1 corresponds to 1997, and so on. This model is valid for the years from 1996 to 2000. Determine the earnings for 2000. Round to two decimal places if necessary.
A. $2.68 million
B. $3.22 million
C. $2.83 million
D. $2.52 million

Math
FunctionsEmployees of a publishing company received an increase in salary of 5% plus a bonus of $800. Let S(x) = 1.05x+800 represent the new salary in terms of the previous salary x. Find and interpret S(20,000).
A. $18,286; If an employee's old salary was $18,286, then his/her new salary was $20,000 after the increase and bonus.
B. $30,800; If an employee's old salary was $30,800, then his/her new salary was $20,000 after the increase and bonus.
C. $21,800; If an employee's old salary was $20,000, then his/her new salary was $21,800 after the increase and bonus.
D. $20,800; If an employee's old salary was $20,000, then his/her new salary was $20,800 after the increase and bonus.

Math
FunctionsJonny is writing a program for a video game. For one part of the game he uses the rule given below to move objects on the screen.
Showing all your work, give the output that the rule gives for the inputs.
(x, y) → (x-7.5, y + 6.8)
First input: (5.4, 3.1)
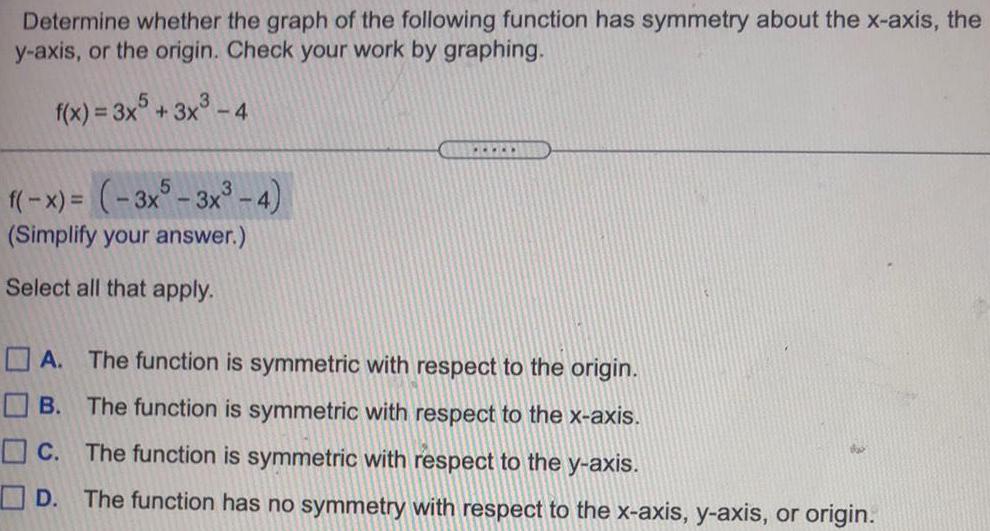
Math
FunctionsDetermine whether the graph of the following function has symmetry about the x-axis, the
y-axis, or the origin. Check your work by graphing.
f(x) = 3x5 + 3x³-4
f(-x) =
A. The function is symmetric with respect to the origin.
B. The function is symmetric with respect to the x-axis.
C. The function is symmetric with respect to
y-axis.
D. The function has no symmetry with respect to the x-axis, y-axis, or origin.

Math
FunctionsDetermine a polynomial f that satisfies the following properties. (Hint: Determine the degree
of f. Then substitute a polynomial of that degree and solve for its coefficients.)
f(f(x)) = 9x-12
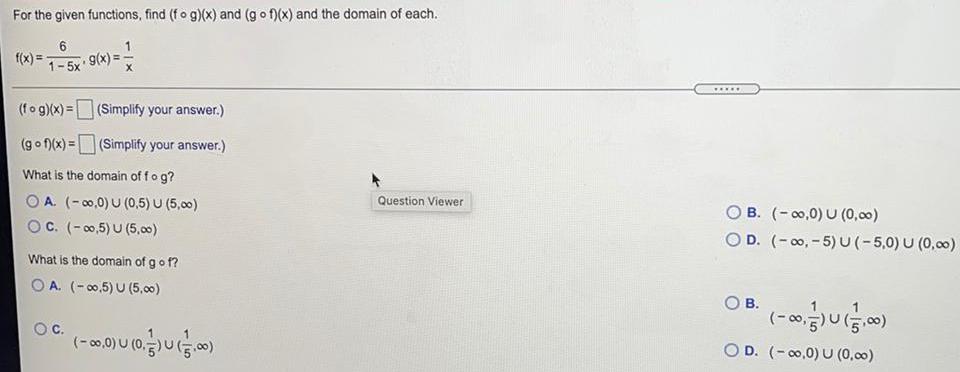
Math
FunctionsFor the given functions, find (fog)(x) and (gof)(x) and the domain of each.
f(x) =6/1 - 5x• 89(x) =
(fog)(x) =
(gof)(x) =
What is the domain of fog?
OA. (-∞0,0) U (0,5) U (5,00)
OC. (-∞0,5) U (5.00)
(Simplify your answer.)
(Simplify your answer.)
What is the domain of g of?
OA. (-∞0.5) U (5,00)
O C.
(-∞0,0) U (0.5) (5.00)
Question Viewer
*****
OB. (-∞0,0) U (0,00)
OD. (-∞, -5) U (-5,0) U (0,00)
O B.
(-80,5) (5,00)
D. (-∞,0) U (0,00)

Math
FunctionsLet s(1) give the number of acres of wetlands in a state in year 1. Assume that the area of wetlands goes down over time. What does the statement tell you about the wetlands?
This tells us that between year t = 13 and t = 33, the area of wetlands increased at an average rate of 547 acres per year.
This tells us that between year t =13 and t = 33, the area of wetlands decreased at anverage rate of 547 acres per year.
This tells us that between year t = 13 and t = 33, the area of wetlands increased by 547 acres.
This tells us that between year t = 13 and t = 33, the area of wetlands decreased by 547 acres.
This tells us that between year t = 13 and t = 33, the area of wetlands was 547 acres.
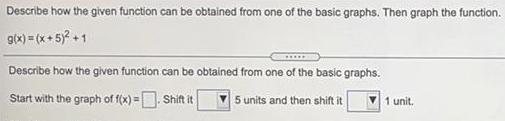
Math
FunctionsDescribe how the given function can be obtained from one of the basic graphs. Then graph the function.
g(x) = (x + 5)² +1
Describe how the given function can be obtained from one of the basic graphs.
Start with the graph of f(x) =

Math
FunctionsDescribe how the graph of g(x) = 1/X+2 - 3 can be obtained from the graph of f(x) = 1/X
How can the graph of g(x)=
A. Shift the graph right 2 units and up 3 units.
B. Shift the graph right 2 units and down 3 units.
C. Shift the graph left 2 units and up 3 units.
D. Shift the graph left 2 units and down 3 units.
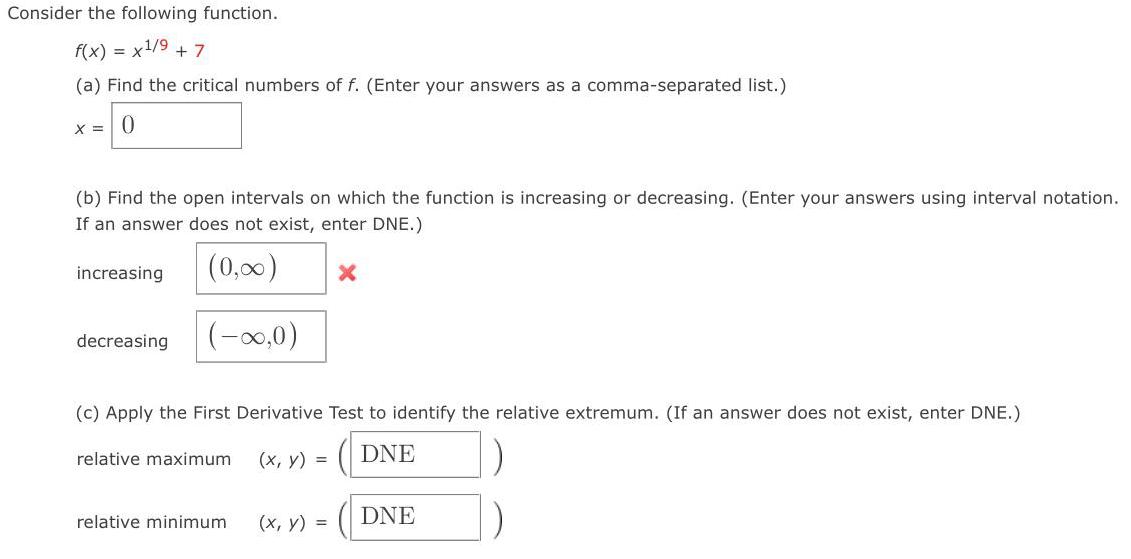
Math
FunctionsConsider the following function.
f(x) = x¹/9 + 7
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
x = 0
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation If an answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum (x, y) =

Math
FunctionsDetermine whether fhas an inverse function. If it does, find the inverse function and state any restrictions on its
domain.

Math
FunctionsTo determine the critical numbers of g(x), set g'(x) equal to zero and solve for x.
Since there is no point for which g'(x) does not exist, x = 1 is the only critical number. Thus, the number line
can be divided into two intervals (-∞, 1) and (1, ∞). Determine the sign of g'(x) at one test value in each of
the two intervals.
First consider the interval (-∞, 1). Let x = 0.
Since g'(0) < 0, for which interval is the function decreasing. (Enter your answer using interval notation.)
Now consider the interval (1, ∞). Let x = 2.
Since g'(2) > 0, for which interval is the function increasing.

Math
FunctionsConsider the following function.
f(x) =x13/13-lnx
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
x =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation.
If an answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify all relative extrema. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum (x, y) =
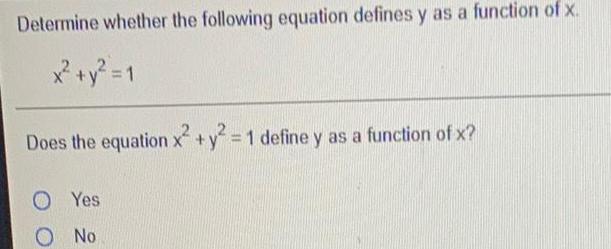
Math
FunctionsDetermine whether the following equation defines y as a function of x.
x² + y² = 1
Does the equation x²+y²=1 define y as a function of x?
Yes
No
![Question: Find the polynomial function, f, such that there is a local minimum at x = 1, a local
maximum at x = 2, a maximum value f(0) = 18, and a minimum value (root) is f(3) = 0. All on the
interval [0,3]](https://media.kunduz.com/media/sug-question/raw/54391041-1658047331.2996638.jpeg?w=256)
Math
FunctionsQuestion: Find the polynomial function, f, such that there is a local minimum at x = 1, a local
maximum at x = 2, a maximum value f(0) = 18, and a minimum value (root) is f(3) = 0. All on the
interval [0,3]
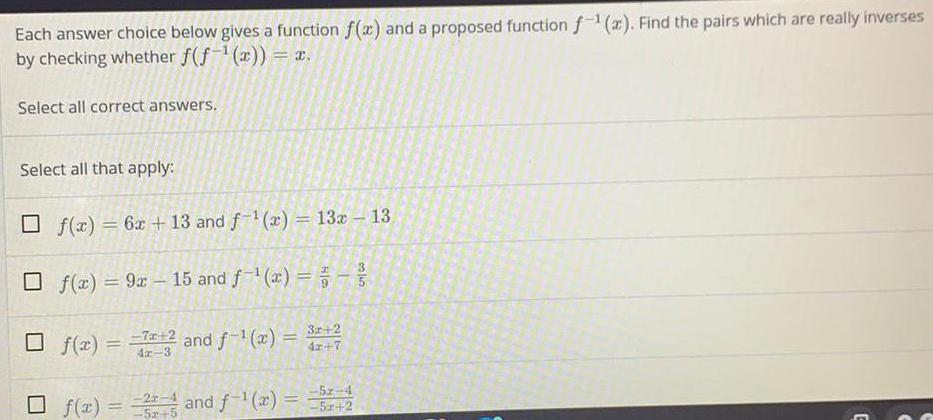
Math
FunctionsEach answer choice below gives a function f(x) and a proposed function f-¹(a). Find the pairs which are really inverses by checking whether f(f(x)) = x.
Select all correct answers.
Select all that apply:
Math
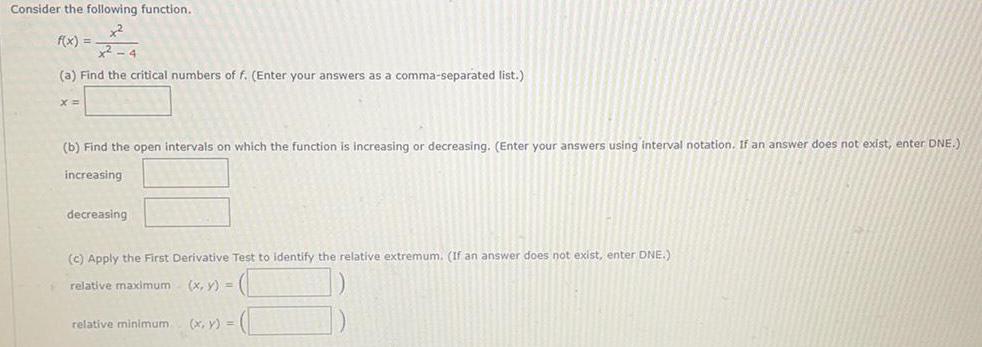
FunctionsConsider the following function.
f(x) =
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
x=
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum
(x, y) =
relative minimum. (x, y) =

Math
FunctionsIn a class of 120 students, everybody would take two hamburgers if the price were zero, and no one would
buy hamburgers if the price were $4 or more.
Assume that the class demand curve for hamburgers is linear and give a formula
(a) (3 pts) describing quantity as a function of price (demand curve)
(b) (3 pts) describing price as a function of quantity (this is sometimes called the inverse demand curve)
(1 pt) Explain what the equation tells you for the demand for hamburgers when the price is $3.99.
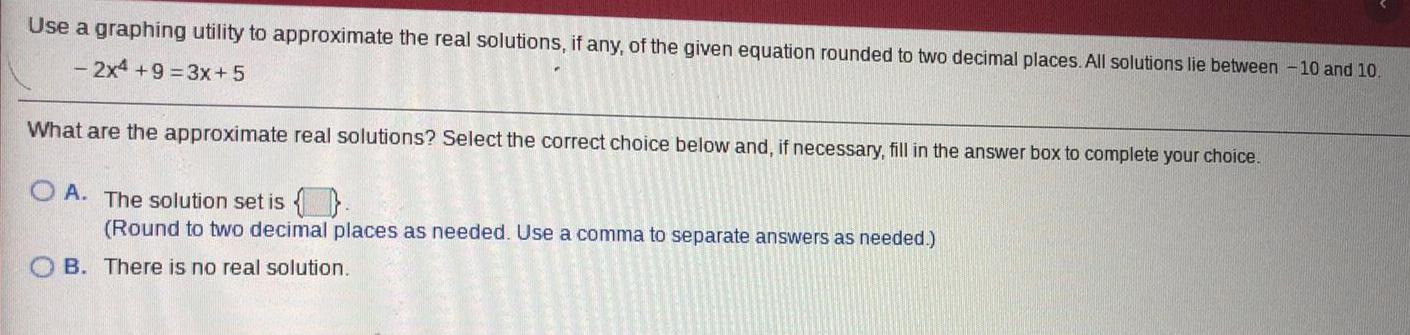
Math
FunctionsUse a graphing utility to approximate the real solutions, if any, of the given equation rounded to two decimal places. All solutions lie between -10 and 10.
- 2x4+9=3x+5
What are the approximate real solutions? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is {}.
(Round to two decimal places as needed. Use a comma to separate answers as needed.)
B. There is no real solution.
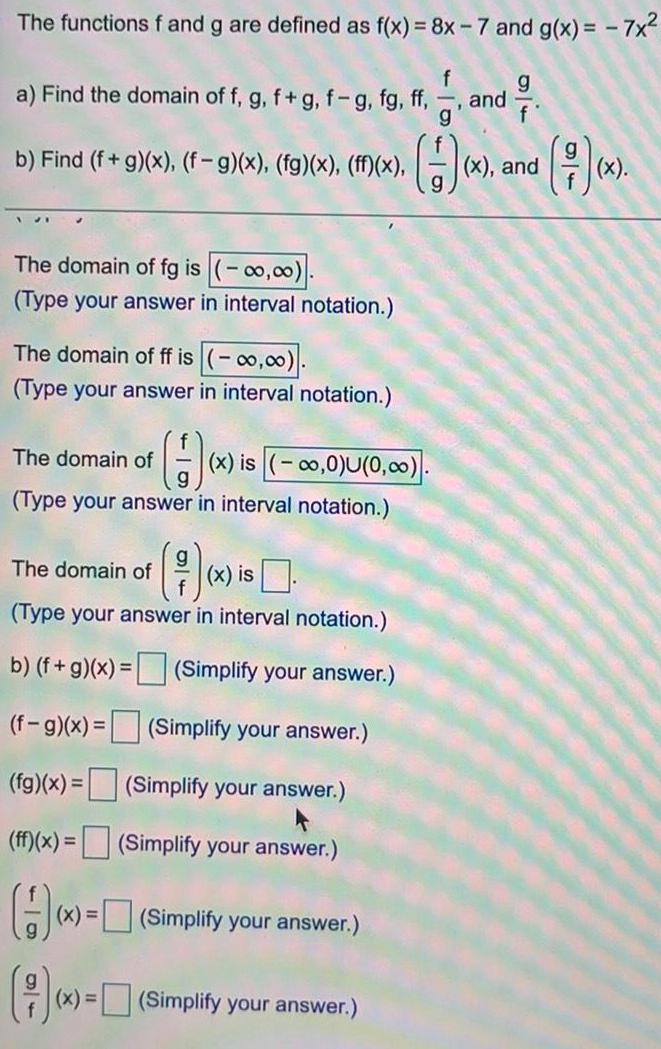
Math
FunctionsThe functions f and g are defined as f(x) = 8x - 7 and g(x) = - 7x²
a) Find the domain of f, g, f + g, f-g, fg, ff, f/g and g/f
b) Find (f+g)(x), (f-g)(x), (fg)(x), (ff)(x), (f/g)(x), and (g/f)(x).
The domain of fg is ().
(Type your answer in interval notation.)
The domain of ff is ()
(Type your answer in interval notation.)
The domain of (f/g)(x) is ().
The domain of (g/f)(x) is.
(Type your answer in interval notation.)
b) (f+g)(x) = (Simplify your answer.)
(f-g)(x) = (Simplify your answer.)
(fg)(x) = (Simplify your answer.)
(ff)(x) = (Simplify your answer.)
(f/g) (x) = (Simplify your answer.)
(g/f) (x)= (Simplify your answer.)

Math
FunctionsFind the composite functions (f. g) and (g. f). What is the domain of each composite function? (Enter your answer using interval
notation.)
domain
f(x): =
(f. g)(x) =
domain
X
g(x) = x² - 25
(g. f)(x) =
8
Are the two composite functions equal?
Yes
No
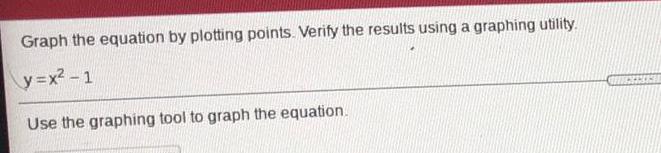
Math
FunctionsGraph the equation by plotting points. Verify the results using a graphing utility.
y=x²-1
Use the graphing tool to graph the equation.
![Find the domain and range for f (x) = -3 | x-2 | +5.
Domain (-∞0,00), Range (-∞0,5]
Domain (-00,00), Range (-∞o, -3]
O Domain (-∞0,2], Range (-∞0,-3]
Domain (-∞0,00), Range [5,00)](https://media.kunduz.com/media/sug-question/raw/54123541-1658000669.8680816.jpeg?w=256)
Math
FunctionsFind the domain and range for f (x) = -3 | x-2 | +5.
Domain (-∞0,00), Range (-∞0,5]
Domain (-00,00), Range (-∞o, -3]
O Domain (-∞0,2], Range (-∞0,-3]
Domain (-∞0,00), Range [5,00)

Math
FunctionsDetermine the roots and multiplicity of each root for f(x) = (x - 2)²(x + 5) ³.
Root x = 4 with multiplicity 2 and root x =
Root x = 2 with multiplicity 8 and root x =
Root x -
Root x
= 2 with multiplicity 4 and root x =
3 with multiplicity -5.
-5 with multiplicity 15.
-5 with multiplicity 3.
-2 with multiplicity 4 and root x = -5 with multiplicity 3.

Math
FunctionsDetermine the end behavior of f(x) = -x¹4 - 3x7 - 10x² + 10.
O The left end extends down and the right end extends up.
O Both ends extend up.
O The left end extends up and the right end extends down.
O
Both ends extend down.

Math
Functions4. Let: N→ R be defined by f(x) = x². Range of the function among the following is
a. {1, 4, 9, 16,...}
b. {1, 4, 8, 9, 10,...}
c. {1, 4, 9, 15, 16,...}
d. {1, 4, 8, 16,...}

Math
Functions3
Use function notation to rewrite the function y =
-X-
1
using h as the function name.
The function written in function notation is.
(Use integers or fractions for any numbers in the expression. Do not simplify.)

Math
FunctionsFor the following exercises, find functions f(x) and g(x) so the given functions can be expressed as
h(x) = f(g(x)). There are multiple possible answers. If the answers require exponents, enter the answer with an
exponent in f(x) but not in g(x).
h(x) =
f(x) =
g(x)
=
5
(x - 2)³
Preview
Preview

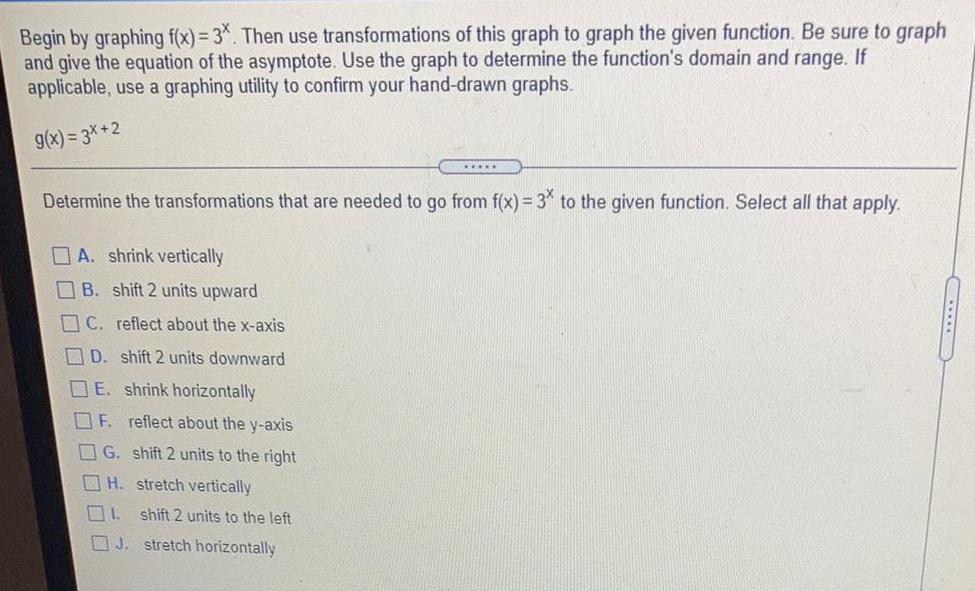
Math
FunctionsBegin by graphing f(x)=3*. Then use transformations of this graph to graph the given function. Be sure to graph
and give the equation of the asymptote. Use the graph to determine the function's domain and range. If
applicable, use a graphing utility to confirm your hand-drawn graphs.
g(x)=3x+2
Determine the transformations that are needed to go from f(x)=3* to the given function. Select all that apply.
A. shrink vertically
B. shift 2 units upward
C. reflect about the x-axis
*****
D. shift 2 units downward
E. shrink horizontally
F. reflect about the y-axis
G. shift 2 units to the right
H. stretch vertically
1.
shift 2 units to the left
J. stretch horizontally

Math
FunctionsDescribe how to transform the graph of y = e² on to the graph y = -e²+¹ 4.
The graph has a vertical shift down 4 units, a reflection over the x axis and a horizontal shift
right 1 unit.
The graph has a vertical shift down 4 units, a reflection over the x axis and a horizontal shift to
the left 1 unit.
The graph has a vertical shift up 4 units, a reflection over the y axis and a horizontal shift right
one unit.
The graph has a vertical shift up 4 units, a reflection over the x axis and a horizontal shift to the
left 1 unit.

Math
FunctionsSolve the following by graphing.
If one solution, type that point in for both points.
If no solution, type in "NS".
x² - y = 3
2x - y = 3

Math
FunctionsSelect the answers that best complete the given statement.
The exponential function f with base b is defined by f(x)=, b>0 and b# 1. Using interval notation, the domain of this function is and the range is