Functions Questions and Answers
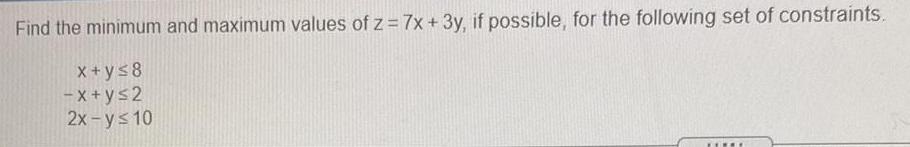
Math
FunctionsFind the minimum and maximum values of z = 7x + 3y, if possible, for the following set of constraints.
x+y≤8
-x+y≤2
2x-y≤ 10

Math
FunctionsIf f(x)=x²-5x and g(x) = 8 - x³, evaluate the following.
a. (f+g)(4)
b. (g-f)(3)
c. (f.g)(-2)
d. (g/f)(-4)
a. (f+g)(4) = (Simplify your answer.)

Math
FunctionsEvan earns $12 an hour plus $15 an hour for every hour of overtime. Overtime hours are any hours more than 30 hours for the week.
Part A: Create an equation that shows the amount of money earned, M, for working x hours in a week when there is no overtime.
Part B: Create an equation that shows the amount of wages earned, T, for working y hours of overtime. Hint: Remember to include in the equation the amount earned from working 30 hours.
Part C: Evan earned $510 in 1 week. How many hours (regular plus overtime) did he work?

Math
FunctionsIn 1993, the moose population in a park was measured to be 4750. By 1999, the population was measured again to be 4030. If the population continues to change linearly:
A.) Find a formula for the moose population, P, in terms of t, the years since 1990.
P(t) =
B.) What does your model predict the moose population to be in 2004?

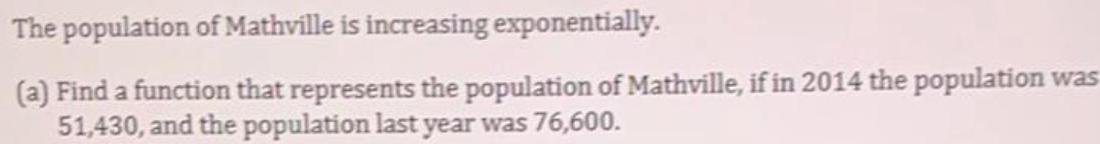
Math
FunctionsThe population of Mathville is increasing exponentially
. (a) Find a function that represents the population of Mathville, if in 2014 the population was 51,430, and the population last year was 76,600.
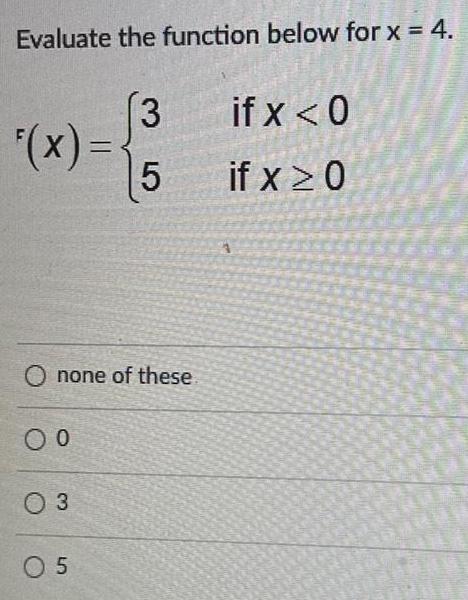
Math
FunctionsEvaluate the function below for x = 4.
F(x)= 5 {3 if x < 0
5 if x ≥ 0
none of these.
0
3
5

Math
FunctionsLet y = 2(x-3)^2-6.
Is the given relation a function? Is it one-to-one? Explain completely. If it is not one-to-one, determine a possible restriction on the domain such that the relation is one- to-one.

Math
FunctionsA business that manufactures small alarm clocks has weekly fixed costs of $4000. The average cost per clock for the business to manufacture x clocks is described by 0.6x + 4000/X
a. Find the average cost when x= 100, 1000, and 10,000.
b. Like all other businesses, the alarm clock manufacturer must make a profit. To do this, each clock must be sold for at least 50c more than what it costs to manufacture. Due to competition from a larger company, the clocks can be sold for $1.50 each and no more. Our small manufacturer can only produce 2000 clocks weekly. Does this business have much of a future? Explain.
a. The average cost when x= 100 is $

Math
FunctionsGiven a polynomial that has zeros of -5, 3i, and -3i and has a value of 432 when x = 3. Write the polynomial in standard form ax^n + bx^n-1 +....

Math
FunctionsGraph the following quadratic function.
f(x) = x² + 4x
Find the vertex of the function.

Math
FunctionsYour teacher will give you a set of four function machines. Your team's job is to get a specific output by putting those machines in a particular order so that one machine's output becomes the next machine's input. As you work, discuss what you know about the kind of output each function produces to help you arrange the machines in an appropriate order. The four functions are reprinted below.
f(x)=√x
h(x) = 2x - 7
g(x) = -(x - 2)²
k(x) = - x/2 -1
a. In what order should you stack the machines so that when 6 is dropped into the first machine, and all four machines have had their effect, the last machine's output is 11?
b. What order will result in a final output of 131, 065 when the first input is 64?
Math
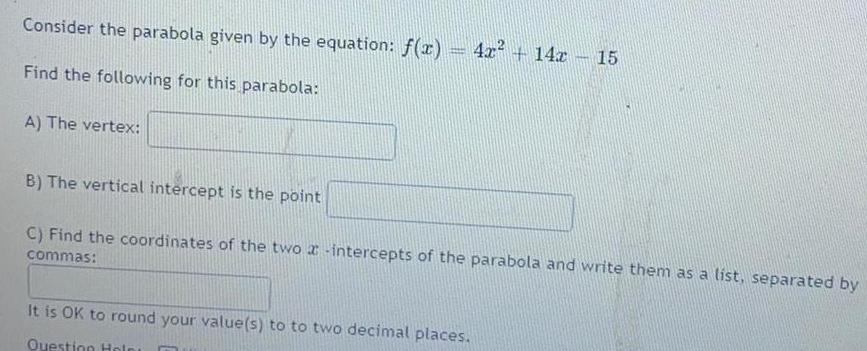
FunctionsConsider the parabola given by the equation: f(x) = 4x² + 14x -15
Find the following for this parabola:
A) The vertex:
B) The vertical intercept is the point
C) Find the coordinates of the two a -intercepts of the parabola and write them as a list, separated by

Math
Functions7. A catering company is setting up for a wedding. They expect 150 people to attend. They can provide small tables that seat 6 people and large tables that seat 10 people.
a. Find a combination of small and large tables that seats exactly 150 people.
b. Let x represent the number of small tables and y represent the number of large tables. Write an equation to represent the relationship between x and y.
c. Explain what the point (20, 5) means in this situation.
d. Is the point (20, 5) a solution to the equation you wrote? Explain your reasoning.

Math
FunctionsCharlotte is in the business of manufacturing phones. She must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. The labor and materials cost $100 for each phone manufactured, and the total cost of producing 8 phones in a day would be $1300. Write an equation for C, in terms of p, representing total cost, in dollars, of producing p phones in a given day.

Math
FunctionsA chef bought $17.01 worth of ribs and chicken. Ribs cost 1.89 per pound and chicken costs 0.90 per pound. The equation 0.9c+1.89r = 17.01 represents the relationship between the quantities in this situation.
Show that each of the following equations is equivalent to 0.9c+1.89r = 17.01. Then, explain when it might be helpful to write the equation in these forms.
a. c = 18.9 -2.1r
b. r = -10/21 c+9
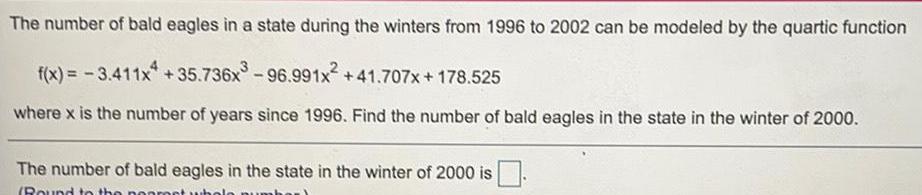
Math
FunctionsThe number of bald eagles in a state during the winters from 1996 to 2002 can be modeled by the quartic function
f(x) = -3.411x4 +35.736x³-96.991x² +41.707x+178.525
where x is the number of years since 1996. Find the number of bald eagles in the state in the winter of 2000.
The number of bald eagles in the state in the winter of 2000 is
(Round to the pooreet whola
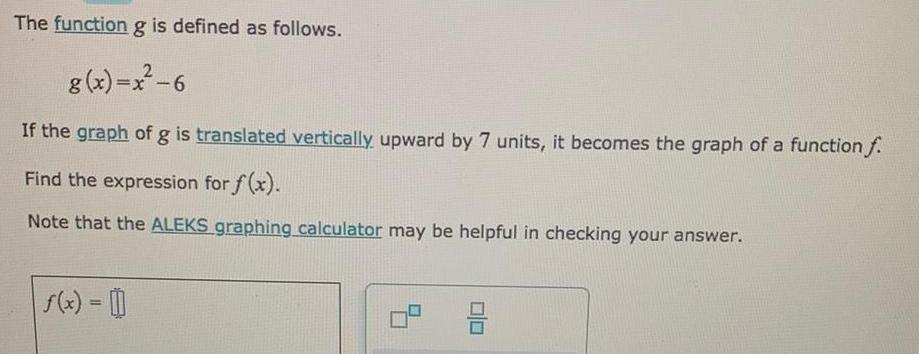
Math
FunctionsThe function g is defined as follows.
g(x)=x²-6
If the graph of g is translated vertically upward by 7 units, it becomes the graph of a function f.
Find the expression for f(x).
Note that the ALEKS graphing calculator may be helpful in checking your answer.
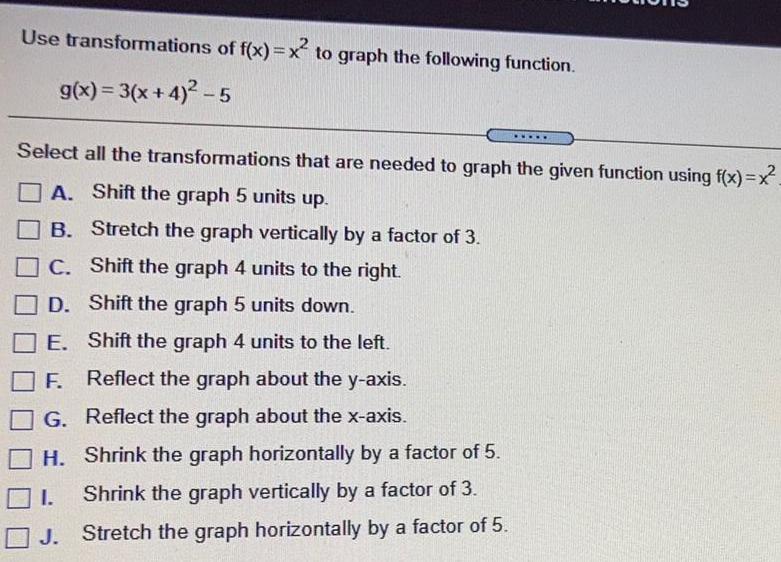
Math
FunctionsUse transformations of f(x)=x² to graph the following function.
g(x)=3(x+4)²-5
Select all the transformations that are needed to graph the given function using f(x)=x²
A. Shift the graph 5 units up.
B.Stretch the graph vertically by a factor of 3.
C. Shift the graph 4 units to the right.
D. Shift the graph 5 units down.
E. Shift the graph 4 units to the left.
F. Reflect the graph about the y-axis.
G. Reflect the graph about the x-axis.
H. Shrink the graph horizontally by a factor of 5.
I. Shrink the graph vertically by a factor of 3.
J. Stretch the graph horizontally by a factor of 5.

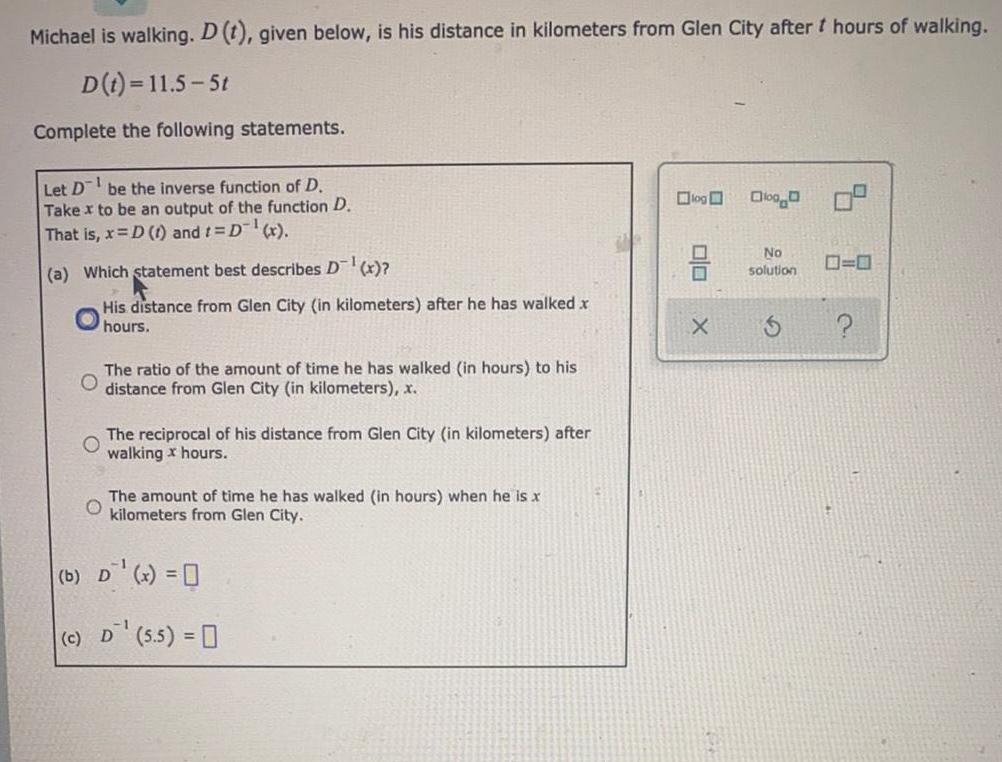
Math
FunctionsMichael is walking. D (t), given below, is his distance in kilometers from Glen City after t hours of walking.
D(t)=11.5-5t
Math
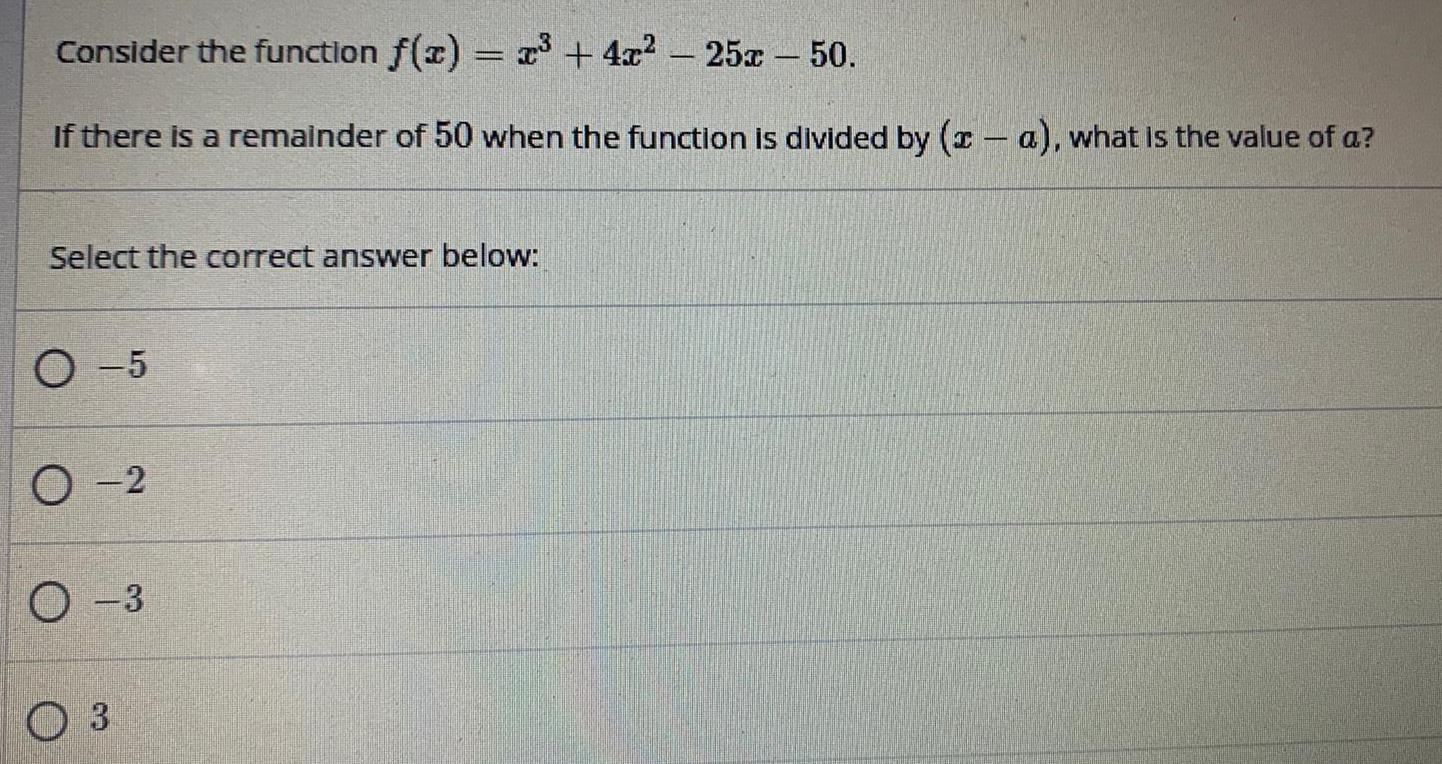
FunctionsConsider the function f(x) = x³ + 4x² - 25x -50.
If there is a remainder of 50 when the function is divided by (x-a), what is the value of a?
Select the correct answer below:
-5
-2
-3
3

Math
FunctionsGiven f(x) = 3x-2x²
a) Evaluate f(-2)
b) The graph of f(x) becomes the function g(x) by a vertical stretch by a factor of 4 and a horizontal translation left 3. Write the equation of g(x) in the form g(x) = ax ² + bx + C.

Math
FunctionsType the correct answer in the box.
Mr. Jensen is a salesperson for an insurance company. His monthly paycheck includes a base salary of $2.175 and a commission of $250 for each policy he sells.
Write an equation, in slope-intercept form, that represents the total amount. y. in dollars, of Mr. Jensen's paycheck in a month when he sells x policies. Do not include dollar signs in the equation.
Math
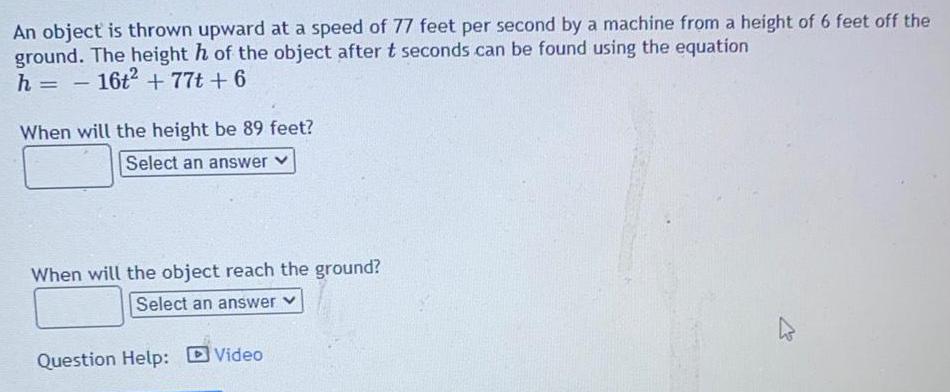
FunctionsAn object is thrown upward at a speed of 77 feet per second by a machine from a height of 6 feet off the ground. The height h of the object after t seconds can be found using the equation
h= - 16t² + 77t + 6
When will the height be 89 feet?
When will the object reach the ground?

Math
FunctionsFor the function f(x) = x + 4x³ + 4x2, answer the following:
h. What are the critical points for f(x)?
i. For what x is f(x) increasing?
j. For what x is f(x) decreasing?
k. Are there any relative maxima/minima? If so, what are the points:
l. On what interval(s) is f(x) concave up? (if none, say so)
m. On what interval is f(x) concave down? (if none, say so)
n. What is the inflection point(s)? (if none, say so)
g. What is the equation of the tangent line to f(x) at x = 1?
h. Sketch the graph and the tangent line
Math
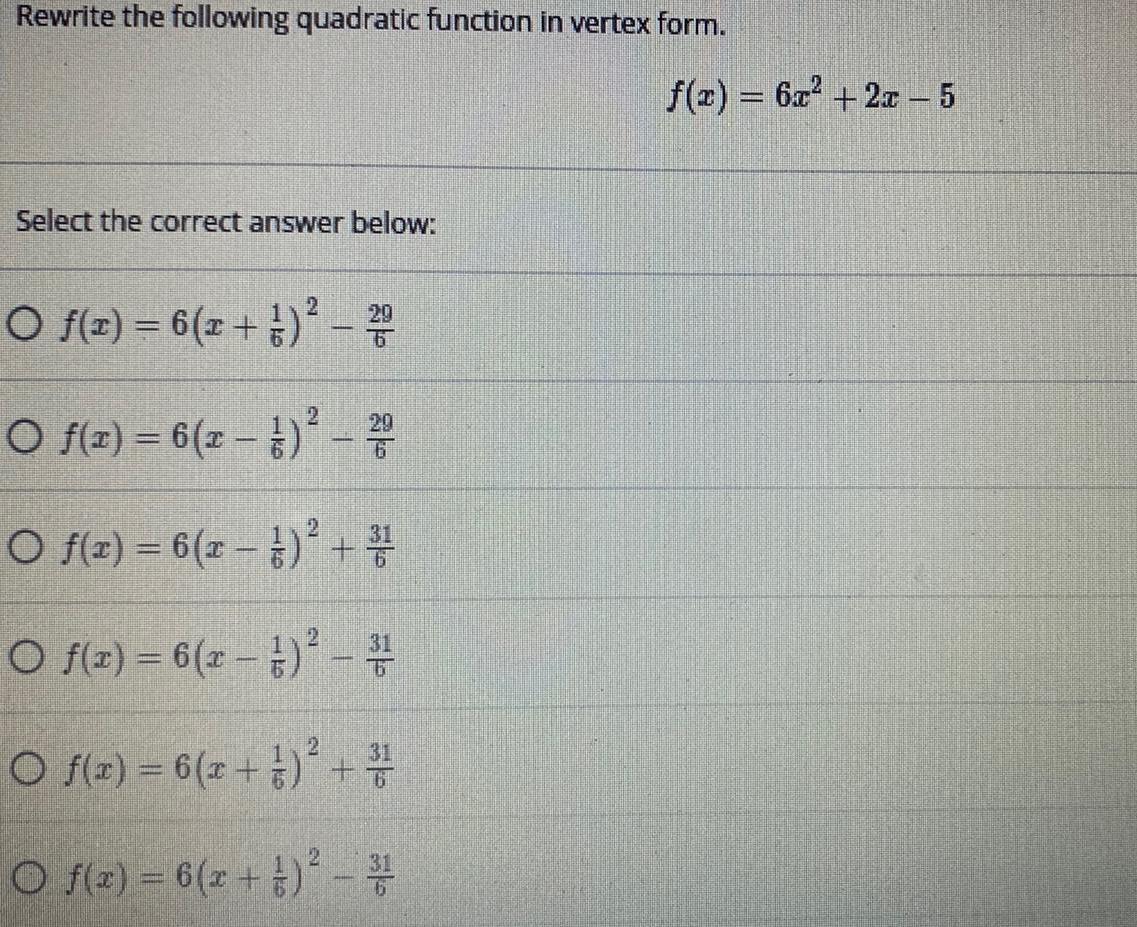
FunctionsRewrite the following quadratic function in vertex form.
f(x) = 6x² + 2x - 5
Select the correct answer below:
f(x) = 6(x + 1/6)² - 29/6
f(x)= 6(x - 1/6)² - 29/6
f(x)= 6(x - 1/6)² + 31/6
f(x) = 6(x - 1/6)² - 31/6
f(x) = 6(x + 1/6)² + 31/6
f(x) = 6(x + 1/6)² - 31/6

Math
FunctionsThe total revenue function for a product is given by R = 520x dollars, and the total cost function for this same product is given by C= 16,000+80x + x², where C is measured in dollars. For both functions, the input x is the number of units produced and sold.
a. Form the profit function for this product from the two given functions.
b. What is the profit when 31 units are produced and sold?
c. What is the profit when 46 units are produced and sold?
d. How many units must be sold to break even on this product?
a. Write the profit function.
P(x) =
(Simplify your answer.)

Math
Functions(a) Find the inverse function of f(x) = 3x - 3.
ƒ-¹(x) =
(b) The graphs of f and f-¹ are symmetric with respect to the line defined by y =

Math
FunctionsGiven the function f(x) = 7x - 5 and the function g(x) = 9x² + 6x +7 determine each of the following.
a) Evaluate f(9) + g(13) f(9) + g(13)=
b) Evaluate f(7) - g(8) f(7) - g(8) =
c) Evaluate f(x) + g(x) f(x) + g(x) =
d) Evaluate f(x) - g(x) f(x) - g(x) =
e) Evaluate g(x) - f(x) g(x) - f(x) =

Math
FunctionsA small ice cream company estimates its revenue (the money earned from selling ice cream) to be R = 4x dollars, where x = the number of ice creams sold. The ice cream company estimates its costs by C = 2.5x + 750 dollars, where x = the number of ice creams sold.
What is the selling price of each ice cream? dollars
The profit from selling a ice creams is P =
In order to break even, the company must sell at least ice creams.
What is the margin of profit if 400 ice creams are sold? dollars. (If a loss, indicate with a negative sign)
What is the margin of profit if 600 ice creams are sold? dollars. (If a loss, indicate with a negative sign)
Math
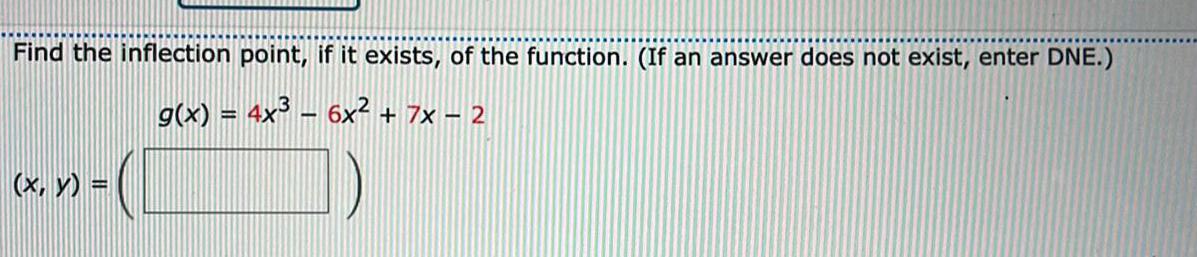
FunctionsFind the inflection point, if it exists, of the function. (If an answer does not exist, enter DNE.)
g(x) = 4x³ − 6x² + 7x − 2
(x, y) =
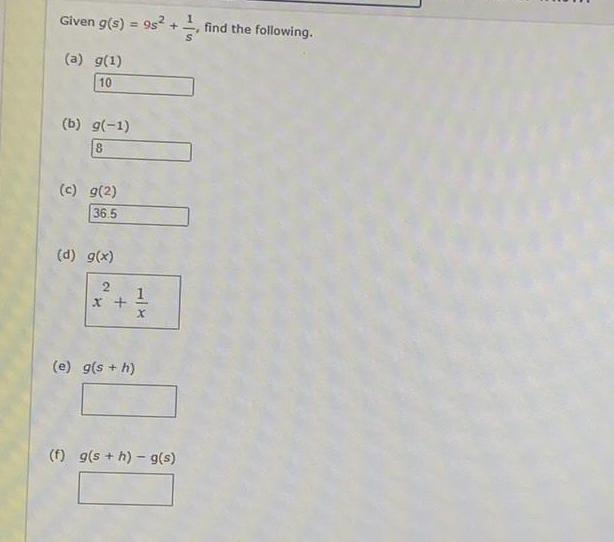
Math
FunctionsGiven g(s) = 9s² + 1/s , find the following.
(a) g(1)
(b) g(-1)
(c) g(2)
(d) g(x)
(e) g(s + h)
(f) g(s+h)-g(s)

Math
FunctionsIf f(x) = x+8 and g(x) = x - 8,
(a) f(g(x)) =
(b) g(f(x)) =
(c) Thus g(x) is called an function of f(x)
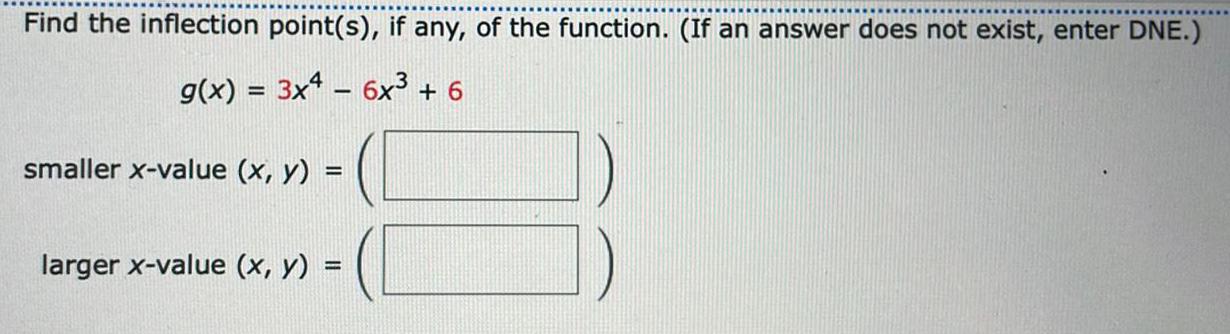
Math
FunctionsFind the inflection point(s), if any, of the function. (If an answer does not exist, enter DNE.)
g(x) = 3x^4 - 6x³ + 6
smaller x-value (x, y) =
larger x-value (x, y) =

Math
FunctionsFactor out the greatest common factor. If the greatest common factor is 1, just retype the polynomial.
3q³ - 9q

Math
FunctionsLet f(x) = (x-4)²
Find a domain on which f is one-to-one and non-decreasing.
Find the inverse of f restricted to this domain.
ƒ-¹(x) =
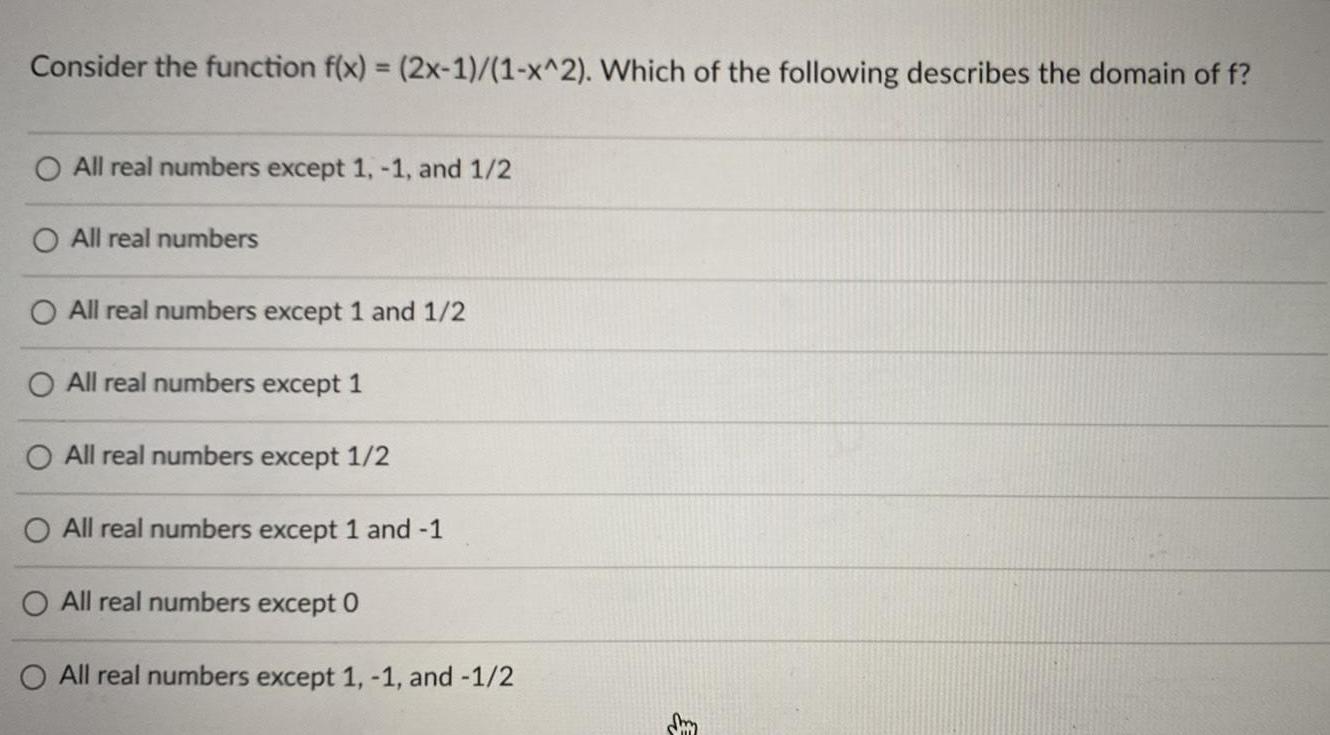
Math
FunctionsConsider the function f(x) = (2x-1)/(1-x^2). Which of the following describes the domain of f?
All real numbers except 1,-1, and 1/2
All real numbers
All real numbers except 1 and 1/2
All real numbers except 1
All real numbers except 1/2
All real numbers except 1 and -1
All real numbers except 0
All real numbers except 1, -1, and -1/2

Math
FunctionsWhen considering the function y=-2ˣ-3, the y-intercept is and the range is
You may either type your answer in the text box using the equation editor or upload a picture of your answer and attach it to this question.
Answers should be written/typed in the following manner:
Function: y=-2ˣ +3
Y-intercept:
Range:
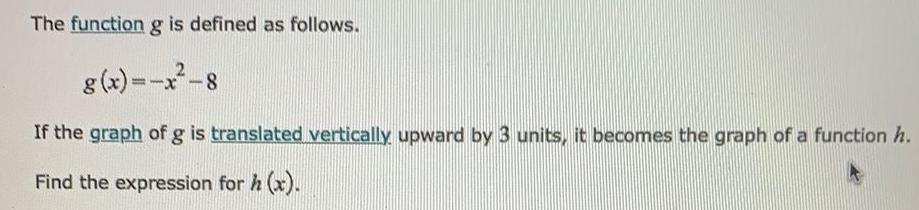
Math
FunctionsThe function g is defined as follows.
g(x) = -x²-8
If the graph of g is translated vertically upward by 3 units, it becomes the graph of a function h.
Find the expression for h (x).

Math
FunctionsA sled accelerates down a hill and then slows down after it reaches a flat portion of ground. The speed of the sled s (t) (in ft/sec) at a time t (in sec) after movement begins can be approximated by:
s(t) =
1.5t for 0≤t≤30
40 / t - 29 for 30<t≤90
Determine the speed of the sled after 20 sec, 30 sec, 40 sec, and 90 sec. Round to 1 decimal place if necessary.
Math
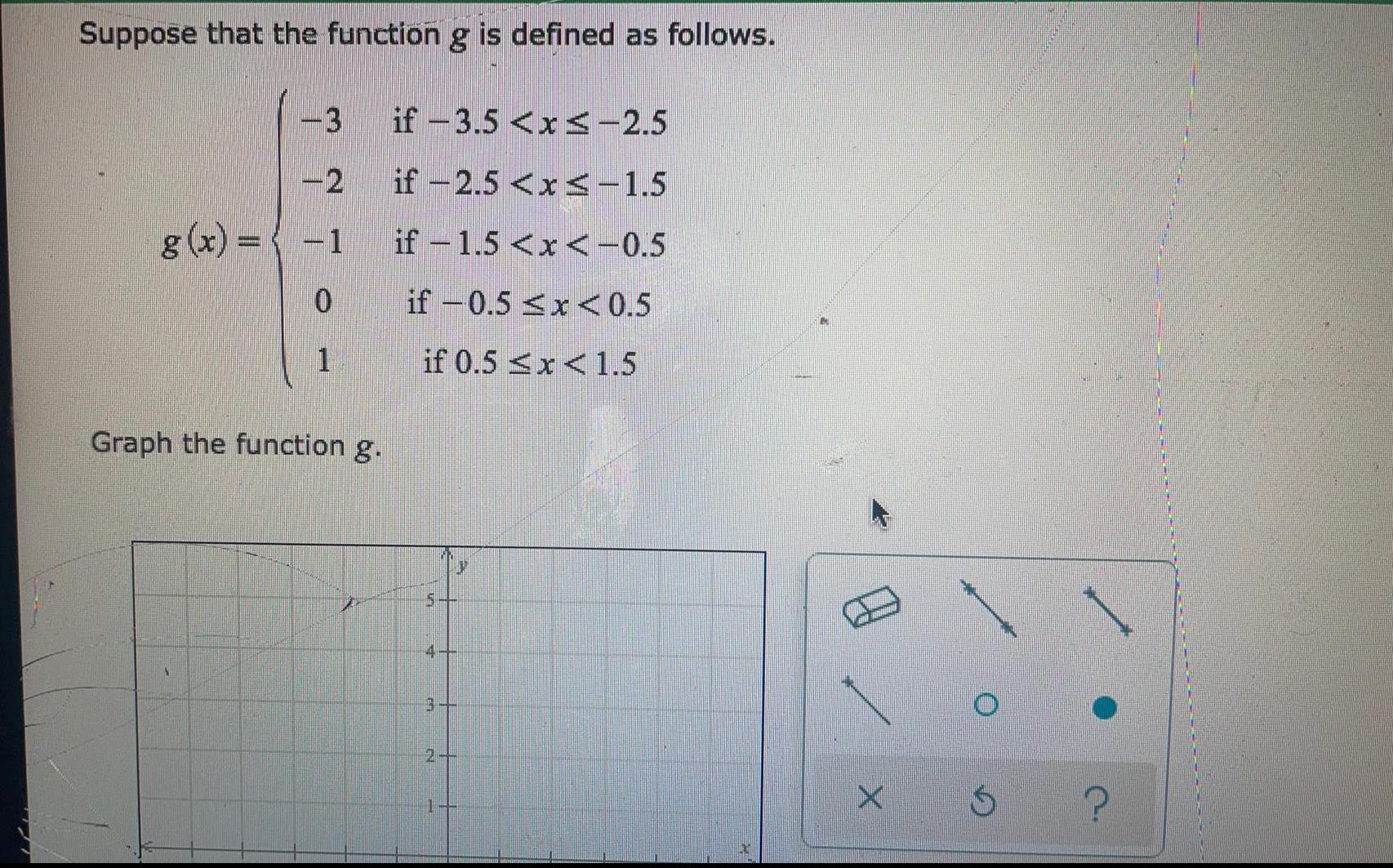
FunctionsSuppose that the function g is defined as follows.
g(x) =
-3 if -3.5 <x< -2.5
-2 if -2.5 < x≤-1.5
-1 if -1.5 <x< -0.5
0 if -0.5 ≤x<0.5
1 if 0.5 <x< 1.5
Graph the function g.

Math
Functionsg(x) = -x³ + 48x
(a) Determine whether g is even, odd, or neither.
(b) There is a local minimum of -128 at -4. Determine the local maximum.
(a) Determine whether g is even, odd, or neither.
Neither
Odd
Even

Math
FunctionsLet the graph of g be a vertical shrink by a factor of 0.25 and a reflection in the x-axis, followed by a translation 2 units right of the graph of f(x) = x². Write a rule for g and identify the vertex.
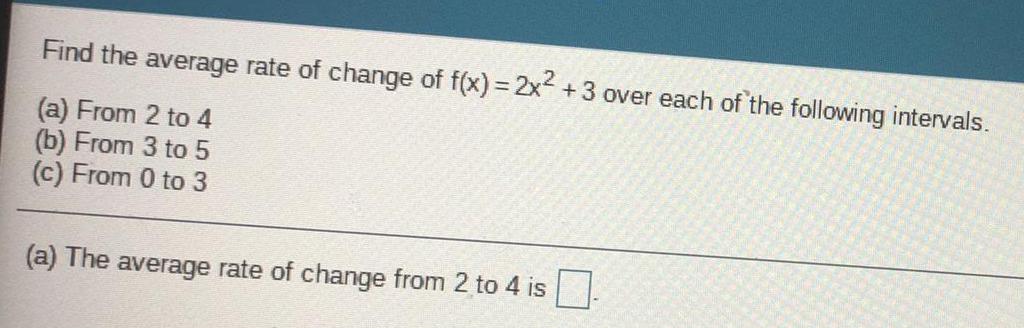
Math
FunctionsFind the average rate of change of f(x) = 2x² + 3 over each of the following intervals.
(a) From 2 to 4
(b) From 3 to 5
(c) From 0 to 3
(a) The average rate of change from 2 to 4 is

Math
FunctionsThe local humane society is restocking on cat food to prepare for kitten season. Very young kittens need kitten formula which costs $3.99 per bottle. Older kittens need wet cat food which costs $1.50 per can.
Part A: Write an algebraic expression to describe how much the humane society will spend preparing for kitten season. Identify the parts of the expression by underlining the coefficient (s), circling the constant(s), and drawing a box around the variable(s).
Part B: How much money (before tax) will the humane society spend if they buy 30 bottles of kitten formula and 120 cans of wet cat food?
Part C: If you add a 7% sales tax to the purchase of bottles of kitten formula and cans of wet cat food, how would the algebraic expression in parts A and B change?
Math
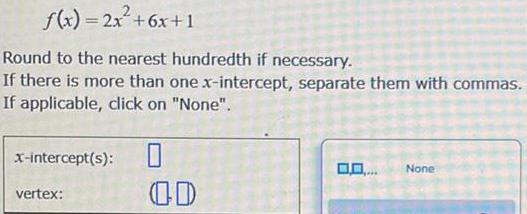
Functionsf(x)=2x²+6x+1
Round to the nearest hundredth if necessary.
If there is more than one x-intercept, separate them with commas.
If applicable, click on "None".
x-intercept(s):
vertex:

Math
FunctionsFind a polynomial function with the zeros - 3, 1, 4 whose graph passes through the point (6,270).

Math
FunctionsConsider this situation: Pistol Pete gained a pretty good reputation as a high school basketball player. An NBA farm team offers him a contract for a $20,000 for the first year, but promises his salary will increase by 75% every year that he plays for up to 10 years.
a. What kind of function could represent this situation? Explain why you think so.
b. Make a table with at least 5 ordered pairs.
c. Draw a graph of this function. Label the y-intercept.
d. What is an appropriate domain for this situation?
e. Write an equation for this function.
Self-assessment:
How did you do on problem 2? Checks:
Math
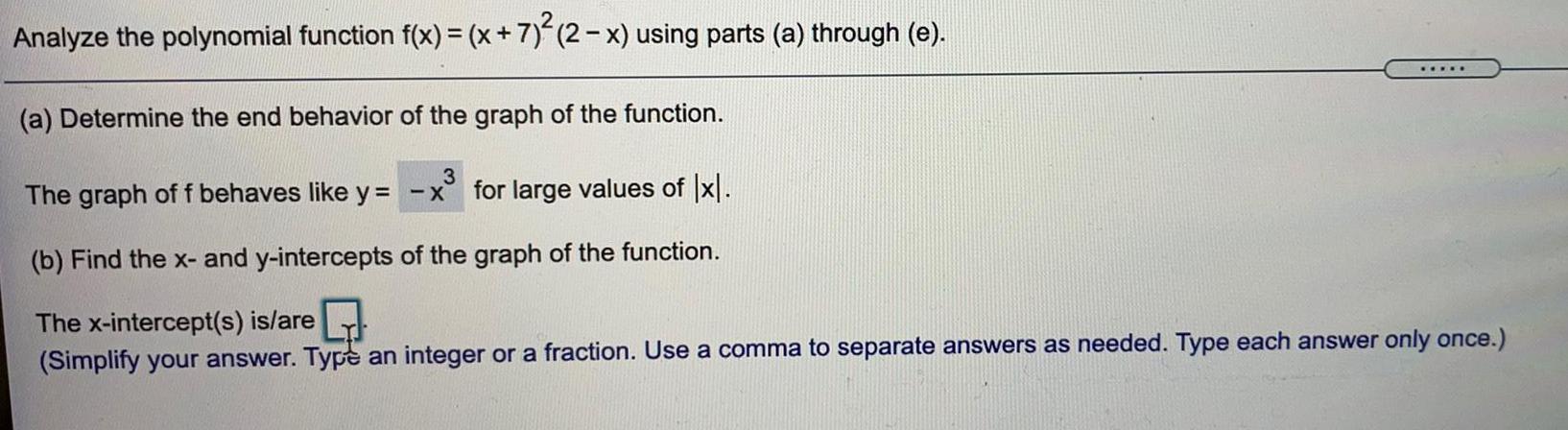
FunctionsAnalyze the polynomial function f(x) = (x + 7)² (2 − x) using parts (a) through (e).
(a) Determine the end behavior of the graph of the function.
(b) Find the x- and y-intercepts of the graph of the function.