Differential equations Questions and Answers

Math
Differential equationsIf a snowball melts so that its surface area decreases at a rate of 8 cm2/min, find the rate (in cm/min) at which the
diameter decreases when the diameter is 9 cm. (Round your answer to three decimal places.)
cm/min

Math
Differential equationsVerify that the given function y is a solution of the differential equation that follows it. Assume that C is an arbitrary constant.
y(t) = C₁ sin 12t+C₂ cos 12t; y''(t) + 144y(t) = 0
*****
Start by substituting y(t) = C₁ sin 12t+C₂ cos 12t into the second term of y''(t) + 144y(t) = 0.
y' (t) +=o

Math
Differential equationsFor the following expression, find the correct partial fraction decomposition.
11y² - 68y +48/ y(y - 4) (4y - 4)
Enter your answer as the sum of fractions with a constant in each numerator and with a linear expression in each denominator.
Provide your answer below:
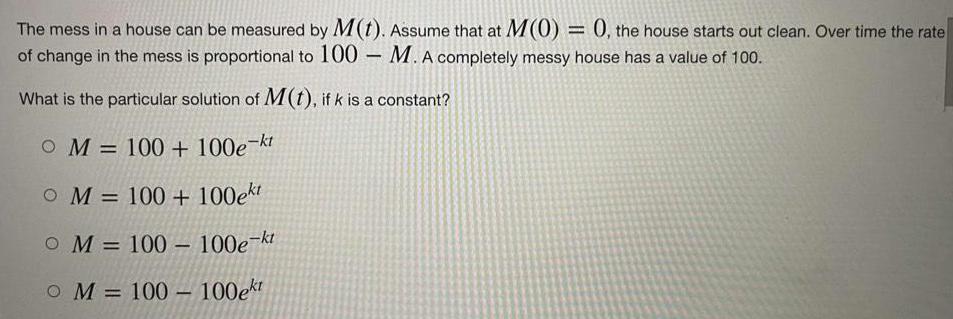
Math
Differential equationsThe mess in a house can be measured by M(t). Assume that at M(0) = 0, the house starts out clean. Over time the rate of change in the mess is proportional to 100 - M. A completely messy house has a value of 100. What is the particular solution of M(t), if k is a constant?
M=100+100e^-kt
M=100+100e^kt
M=100-100e^-kt
M=100-100e^kt
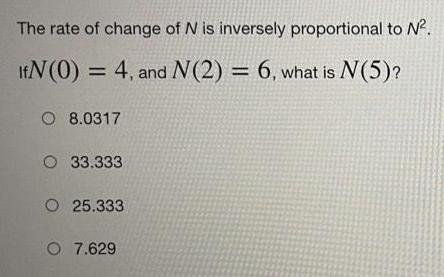
Math
Differential equationsThe rate of change of N is inversely proportional to N².
IfN (0) = 4, and N(2) = 6, what is N(5)?
8.0317
33.333
25.333
7.629
![The percentage of compression on the lumbar vertebral disks causes strain in an adult human. The strain can be measured by S(x) = 7.2956 In(0.0645012 x^0.95 + 1), where x is the physical load in kilograms (kg).
Medical scientists are interested in the rate of change of the strain with respect to the load. This can be found with the derivative S'(x) or ds/dx. The derivative can be found by ...
using the derivative rule for Inf(x)) to get 5'(x) = (7.2956) [1/(0.0645012 x 0.95 + 1)] * [(0.0645012) (0.95) x^(-0.05)), which can be simplified to approximately S'(x) = [0.44705] / [(0.0645012 x^0.95 + 1)*(x^ 0.05]]
using the Chain Rule to get 5'(x) = 7.2956 In(0.0645012 x 0.95 + 1) ((0.0645012)(0.95) x^(-0.05]], which can be simplified to approximately S'(x) = [0.44705 In(0.0645012 x 0.95 + 1)] / [x^0.05]
S'(x) = 7.2956 e^(0.0645012 x^0.95 + 1), where e is the irrational number approximated by 2.71828
using the derivative rule for In(f(x)) to get 5'(x) = (7.2956) [1/(0.0645012 x^0.95 + 1)], which can be simplified to S'(x) = 7.2956/(0.0645012 x^0.95 + 1)](https://media.kunduz.com/media/sug-question/raw/72720892-1657479528.5240192.jpeg?w=256)
Math
Differential equationsThe percentage of compression on the lumbar vertebral disks causes strain in an adult human. The strain can be measured by S(x) = 7.2956 In(0.0645012 x^0.95 + 1), where x is the physical load in kilograms (kg).
Medical scientists are interested in the rate of change of the strain with respect to the load. This can be found with the derivative S'(x) or ds/dx. The derivative can be found by ...
using the derivative rule for Inf(x)) to get 5'(x) = (7.2956) [1/(0.0645012 x 0.95 + 1)] * [(0.0645012) (0.95) x^(-0.05)), which can be simplified to approximately S'(x) = [0.44705] / [(0.0645012 x^0.95 + 1)*(x^ 0.05]]
using the Chain Rule to get 5'(x) = 7.2956 In(0.0645012 x 0.95 + 1) ((0.0645012)(0.95) x^(-0.05]], which can be simplified to approximately S'(x) = [0.44705 In(0.0645012 x 0.95 + 1)] / [x^0.05]
S'(x) = 7.2956 e^(0.0645012 x^0.95 + 1), where e is the irrational number approximated by 2.71828
using the derivative rule for In(f(x)) to get 5'(x) = (7.2956) [1/(0.0645012 x^0.95 + 1)], which can be simplified to S'(x) = 7.2956/(0.0645012 x^0.95 + 1)
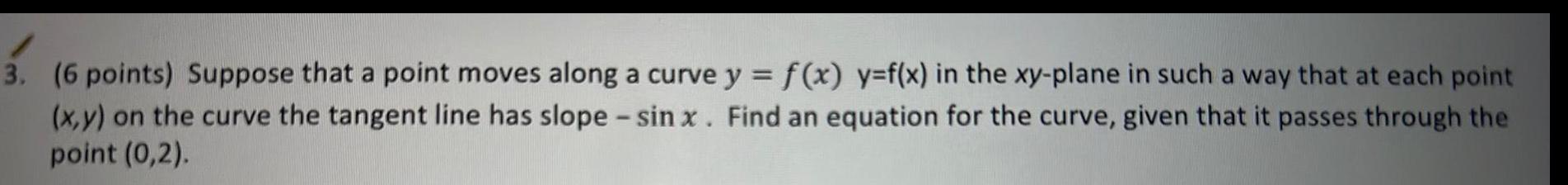
Math
Differential equationsSuppose that a point moves along a curve y = f(x) y=f(x) in the xy-plane in such a way that at each point (x,y) on the curve the tangent line has slope - sinx. Find an equation for the curve, given that it passes through the point (0,2).
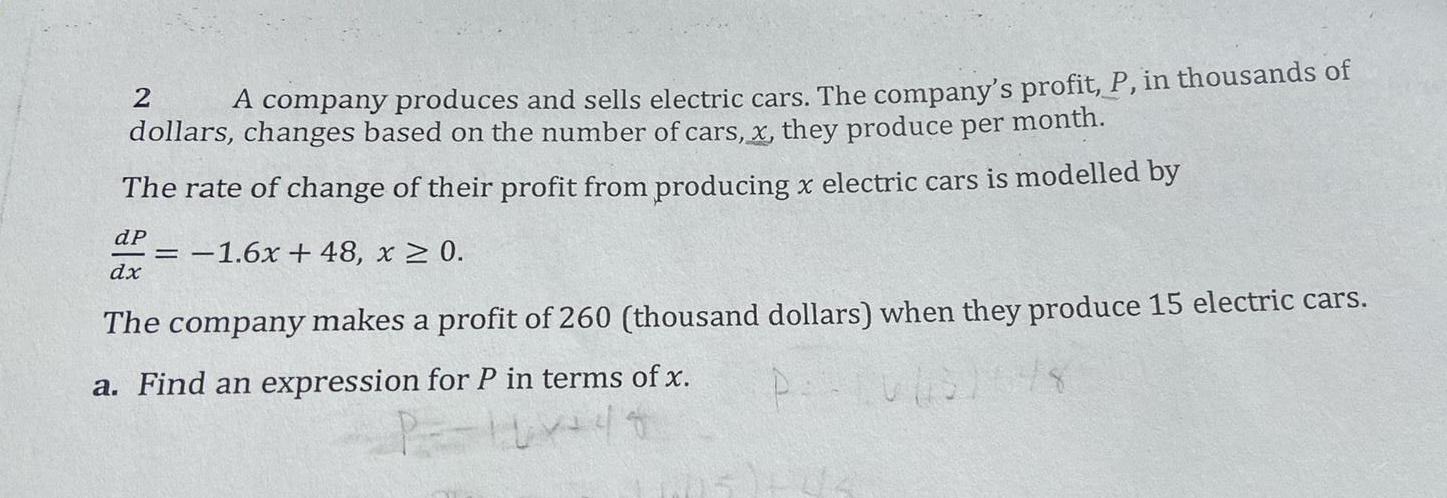
Math
Differential equationsA company produces and sells electric cars. The company's profit, P, in thousands of dollars, changes based on the number of cars, x, they produce per month.
The rate of change of their profit from producing x electric cars is modelled by
dP/dx= -1.6x + 48, x ≥ 0.
The company makes a profit of 260 (thousand dollars) when they produce 15 electric cars.
a. Find an expression for P in terms of x.

Math
Differential equationsThe given family of functions is the general solution of the differential equation on the indicated interval. Find a member of the family that is a solution of the initial-value problem.
y = c₁e^x + c₂e^-x, (-∞, ∞); y" - y = 0, y(0) = 0, y'(0) = 7

Math
Differential equationsIn this problem, y = 1/(x² + c) is a one-parameter family of solutions of the first-order DE y' + 2xy² = 0. Find a solution of the first-order IVP consisting of this differential equation and the given initial condition.
y(3) =1/5
Give the largest interval I over which the solution is defined. (Enter your answer using interval notation.)
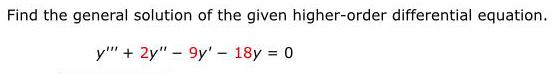
Math
Differential equationsFind the general solution of the given higher-order differential equation.
y''' + 2y" - 9y' - 18y = 0

Math
Differential equationsSolve the given differential equation by using an appropriate substitution. The DE is homogeneous.
(x - y) dx + x dy = 0

Math
Differential equationsThe given two-parameter family is a solution of the indicated differential equation on the interval (-∞, ∞). Determine whether a member of the family can be found that satisfies the boundary conditions. (If yes, enter the solution. If an answer does not exist, enter DNE.)
y = c₁e^x cos x + c₂e^x sin x; y" - 2y' + 2y = 0
(a) y(0) = 1, y '(π) = 0
(b) y(0) = 1, y(π) = -1
(c)y(0) = 1, y(π/2) = 1
(d)y(0) = 0, y(π) = 0

Math
Differential equationsSolve the given initial-value problem. The DE is a Bernoulli equation.
x^2dy/dx - 2xy = 6y^4, y(1) =1/4

Math
Differential equationsSolve the given initial-value problem. The DE is homogeneous.
(x² + 2y²) dx/dy = xy, y(-1) = 3

Math
Differential equationsFind the general solution of the given differential equation.
dy/ dx = 8y
y(x) =
Give the largest interval over which the general solution is defined. (Think about the implications of any singular points. Enter your answer using interval notation.)
Determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)

Math
Differential equationsX
A company manufactures mountain bikes. The research department produced the marginal cost function C'(x) = 600-
10-₁ , 0≤x≤ 900, where C'(x) is in dollars and x is the number of bikes produced per month. Compute the
increase in cost going from a production level of 450 bikes per month to 720 bikes per month. Set up a definite integral and evaluate it.
The increase in cost is $.
......

Math
Differential equationsA candy box is made from a piece of cardboard that measures 37 by 20 inches. Squares of equal size will be cut out of each corner. The sides will then be folded up to form a rectangular box. What size square should be cut
from each corner to obtain maximum volume?
A square with a side of length inches should be cut away from each corner to obtain the maximum volume.
(Round to the nearest hundredth as needed.)
nu

Math
Differential equationsFactor the trinomial. Check the factorization using FOIL multiplication.
✓²-20y+75
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. Y² - 20y+75=
B. The trinomial is prime.

Math
Differential equationsA 39-meter ladder is sliding down a vertical wall so the distance between the bottom of the ladder and the wall
is increasing at 10 meters per minute.
At a certain instant, the bottom of the ladder is 36 meters from the wall.
What is the rate of change of the distance between the top of the ladder and the ground at that instant (in
meters per minute)?

Math
Differential equationsSolve the following differential equations by finding the general solution first then the particular one that satisfies the given constraint in each case.
1. xyy' = ln x, y(1) = 2.
2. y'+y=e^-t, y(0) = 2.


Math
Differential equationsThe total number of acres of genetically modified crops grown worldwide from 1997 to 2003 was changing at the rate given below
in million acres/year.
R' (t) = 2.463² 18.56t+ 47.38
(0 st≤ 6)
The total number of acres of such crops grown in 1997 (t = 0) was 38.8 million acres. How many acres of genetically modified
crops were grown worldwide in 2003? (Round your answer to the nearest whole number.)

Math
Differential equations(1 pt) In cold weather, we feel colder when the wind blows. This is quantified by the wind chill index W which is supposed to predict how cold
we will feel for a given air temperature Tl in degrees Fahrenheit, and wind speed V in miles/hour. The National Weather Service uses the
following formula:
W = 35.74 +0.6215T-35.75V 0.16 +0.4275TV0.16
for T< 50l and V ≥ 3
Use your answer above to do the following question: When the air temperature is 6 degrees, estimate the change in the wind chill index if the
wind speed increases by 2 miles/hour from 19 miles/hour.
Answer:
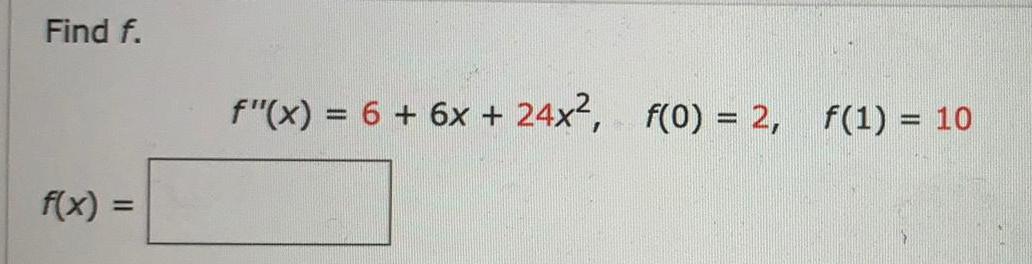
![A chemical plant is adding pollution to a lake at the rate of 35√3 tons per year, where t is the number of years that the plant has been in operation.
(a) Find a formula for the total amount of pollution that will enter the lake in the first t years of the plant's operation. [Hint: Evaluate C so that no pollution has been added at time t = 0.]
P(t) =
(b) Use the formula that you found in part (a) to find how much pollution (in tons) will enter the lake in the first 4 years of the plant's operation. (Round your answer to the nearest whole number.)
P(4) = tons
(c) If all life in the lake will cease when 200 tons of pollution have entered the lake, will the lake "live" beyond 4 years?](https://media.kunduz.com/media/sug-question/raw/60338367-1657218896.555437.jpeg?w=256)
Math
Differential equationsA chemical plant is adding pollution to a lake at the rate of 35√3 tons per year, where t is the number of years that the plant has been in operation.
(a) Find a formula for the total amount of pollution that will enter the lake in the first t years of the plant's operation. [Hint: Evaluate C so that no pollution has been added at time t = 0.]
P(t) =
(b) Use the formula that you found in part (a) to find how much pollution (in tons) will enter the lake in the first 4 years of the plant's operation. (Round your answer to the nearest whole number.)
P(4) = tons
(c) If all life in the lake will cease when 200 tons of pollution have entered the lake, will the lake "live" beyond 4 years?

Math
Differential equationsThe function y = 100e^(-0.045t) models the amount, y, of radioactive material remaining, in grams, as a function of time t, in days. Calculate the half-life of this radioactive material. Round your answer to the nearest tenth.

Math
Differential equationsA flu epidemic hits a college community, beginning with five cases on day t = 0. The rate of growth of the epidemic (new cases per day) is given by the following function r(t), where it is the
number of days since the epidemic began.
r(t) = 22 e0.05t
(a) Find a formula for the total number of cases of flu in the first t days.
F(t) =
(b) Use your answer to part (a) to find the total number of cases in the first 20 days. (Round your answer to the nearest whole number.)
F(20) =
cases

Math
Differential equationsII.
Obtain the general / particular solution for the following differential
equation. Show your solution in bond paper.(15 Points each)
1. (xy + x) dx = (x³y² + x² + y² +1)dy
2. (1+Inx) dx+(1+Iny) dy =0 when y(-2) = -1.

Math
Differential equationsA cone is expanding at the rate of 6 cm³/sec. The formula for the volume of a cone is: What is when r = 2?