İki Kat Açı Formülleri Soruları

Geometri
İki Kat Açı Formüllericos² + 510² € = 1
2+ sin²x-cos²x
2-cos2x
ifadesi aşağıdakilerden
A) O
B) sinx
7.
8.
D) tanx
Lay
cos²x-sin²x = -
cos2+ = -1 2+ = 120 + 360k
21
2
X=6011804
denkleminin çözüm
hangisidir? (k EZ)
AL(RX = FKx}
C)
2-cos2x
=1
2-00524
hangisine eşittir?
C) 1
X:X=F
E) cotx
kümesi aşağıdakilerden
B) {xx=++ kr
XX=T
=F
D)
kл
E) {xx = 7 1+kx}
+ kr
Cos2+=COSRO
24=180-120 +360k
X = 30 +160k / 60 +180k
![38.
5√3=2h₁+2h₂²
3√√3=hith₂
-6.
B
√
C'
D 2 E
A
a
90-
ABCD dikdörtgeninde C köşesi [EB] boyunca katlan-
dığında C noktası C noktasına gelmektedir.
+12=XA) ²0
B)
~=2M-2X = X = 6
6
C)
F
2_IDEI = 2 birim, IABI= 6 birim, IADI = 8 birim oldu-
ğuna göre sin2x değeri kaçtır?
√√2
2
B
8
D)
√3
$35090²
6 1](https://media.kunduz.com/media/question/seo/raw/20230318074427988022-1878599.jpg?w=256)
Geometri
İki Kat Açı Formülleri38.
5√3=2h₁+2h₂²
3√√3=hith₂
-6.
B
√
C'
D 2 E
A
a
90-
ABCD dikdörtgeninde C köşesi [EB] boyunca katlan-
dığında C noktası C noktasına gelmektedir.
+12=XA) ²0
B)
~=2M-2X = X = 6
6
C)
F
2_IDEI = 2 birim, IABI= 6 birim, IADI = 8 birim oldu-
ğuna göre sin2x değeri kaçtır?
√√2
2
B
8
D)
√3
$35090²
6 1
![12. ABCD karesinin [AD] kenarı mavi renkli çemberin mer-
kezinden geçmektedir. [BT ışını T noktasında O merkez-
li çembere teğet, [AC] n [BT = {E}, |BE| = 10 birimdir.
D
B) 5
Of
A
E
C) 6
10
Buna göre, E noktasının karenin [BC] kenarına uzak-
lığı kaç birimdir?
A) 4
B
D) 8
E) 4√5](https://media.kunduz.com/media/question/seo/raw/20230317131903568340-2041978.jpg?w=256)
Geometri
İki Kat Açı Formülleri12. ABCD karesinin [AD] kenarı mavi renkli çemberin mer-
kezinden geçmektedir. [BT ışını T noktasında O merkez-
li çembere teğet, [AC] n [BT = {E}, |BE| = 10 birimdir.
D
B) 5
Of
A
E
C) 6
10
Buna göre, E noktasının karenin [BC] kenarına uzak-
lığı kaç birimdir?
A) 4
B
D) 8
E) 4√5
Geometri
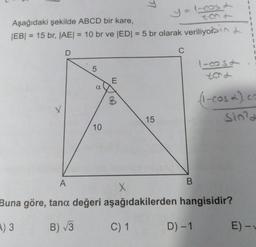
İki Kat Açı FormülleriAşağıdaki şekilde ABCD bir kare,
y=1_casa
|EB| = 15 br, |AE| = 10 br ve |ED| = 5 br olarak veriliyorin
D
5
a
10
E
B
15
C
B
190st
D) -1
(1-cos). co
Sind
A
X
Buna göre, tana değeri aşağıdakilerden hangisidir?
A) 3
B) √3
C) 1
E) -
Geometri
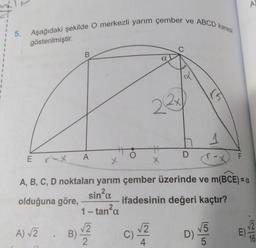
İki Kat Açı Formülleri5. Aşağıdaki şekilde O merkezli yarım çember ve ABCD karesi
B
A
A) √2. B)√2
α
22x
x
c) √/2
C)
4
C
D
x
A, B, C, D noktaları yarım çember üzerinde ve m(BCE) = a
sin²α
olduğuna göre,
ifadesinin değeri kaçtır?
1-tan²α
F
D) V5
5
E)
A)
√2
16

Geometri
İki Kat Açı Formülleri8.
Aşağıdaki dik koordinat düzleminde O merkezli birim çember
verilmiştir.
A
a
y
D) 2-sin(2a)
O
C
B
m(CAB) = a olup ABCD dikdörtgeninin köşeleri birim çember
üzerindedir.
Buna göre, ABCD dikdörtgeninin alanı birimkare türünden
aşağıdakilerden hangisidir?
A) 2tan(2a)
B) 2. sec(a)
C) 2-cosec(a)
E) 2-cos(2a)
Geometri
İki Kat Açı Formülleri√3
2
tala-
- yer
taya
den
geri
of peo
?
k²
x. COS
COSQ =
B
A)
A
m(NPG) = a olduğuna göre, tania kaçtır?
A) 2+√3
B) 4
7/2
50 m
D) 8
1- t
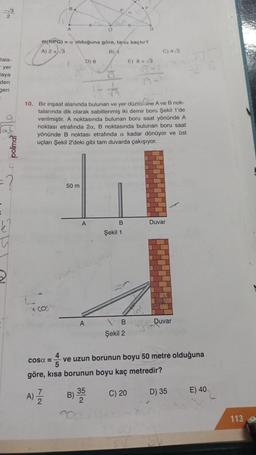
10. Bir inşaat alanında bulunan ve yer düzlemine A ve B nok-
talarında dik olarak sabitlenmiş iki demir boru Şekil 1'de
verilmiştir. A noktasında bulunan boru saat yönünde A
noktası etrafında 2a, B noktasında bulunan boru saat
yönünde B noktası etrafında a kadar dönüyor ve üst
uçları Şekil 2'deki gibi tam duvarda çakışıyor.
A
B)
O
A
P
35
2
B
#1
Şekil 1
B
Şekil 2
G
E) 8+√3
6+1
göre, kısa borunun boyu kaç metredir?
C) 20
C) 4√3
Duvar
ve uzun borunun boyu 50 metre olduğuna
5
Duvar
D) 35
E) 40
113
Geometri
İki Kat Açı Formülleri-2
Å
ÖRNEK 5
A
A) 6
ÖRNEK 6
B) 6√2
6
H
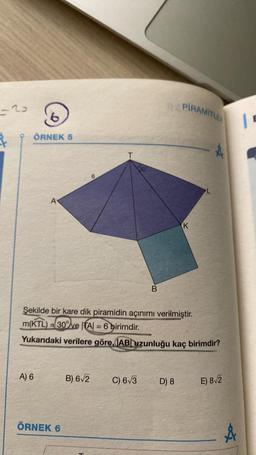
Şekilde bir kare dik piramidin açınımı verilmiştir.
m(KTL) 30%ve |TA| = 6 birimdir.
Yukarıdaki verilere göre, AB uzunluğu kaç birimdir?
30
C) 6√3
B
PIRAMITLES
D) 8
K
E) 8√2
&
"
Geometri
İki Kat Açı Formüllerib
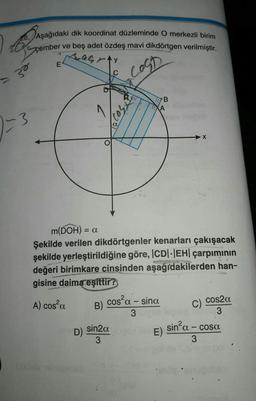
28. Aşağıdaki dik koordinat düzleminde O merkezli birim
ve beş adet özdeş mavi dikdörtgen verilmiştir.
çember
AGAY
Ost
= 30
2-3
E
D)
hodeb niniesbati
m(DOH) = a
Şekilde verilen dikdörtgenler kenarları çakışacak
şekilde yerleştirildiğine göre, |CD|-|EH| çarpımının
değeri birimkare cinsinden aşağıdakilerden han-
gisine daima eşittir?
SENS
A) cos²a
B)
X50231
sin2a
3
LA
cos²a - sina
3
B
E)
cos2α
102.003
C)
sin²a - cosa
3

Geometri
İki Kat Açı Formülleri11
LİMİT YAYINLARI
313k
30.
D
Matematik
20
F
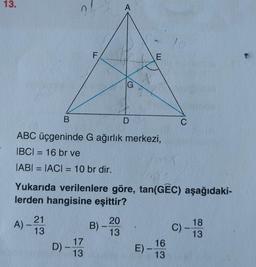
Bir öğrenci şekildeki gibi ABCD karesinin içine
ikizkenarlarının uzunluğu 1 birim ve tepe açısı 40° olan
bir EBF ikizkenar üçgeni çizmiştir.
Daha sonra |DF|, |FC| ve |BC| uzunluklarını sinüs ya da
kosinüs cinsinden bulup |DC| = |BC| eşitliğini
kullanarak bir sonuca ulaşmıştır.
A) √2-sin20° + sin25° = cos25°
B) √2 cos40°-cos25° = sin25°
C) 2-sin20°-sin25° = cos25°
D) 2 cos20° + sin25° = cos40°
E) 2-cos40°-cos25° = sin20°
3
1
Buna göre, öğrencinin ulaştığı sonuç
aşağıdakilerden hangisidir?
6k
40"
Geometri
İki Kat Açı Formülleri13.
A).
21
13
B
ABC üçgeninde G ağırlık merkezi,
IBCI= 16 br ve
IABI= |ACI = 10 br dir.
D) -
F
-
17
13
Yukarıda verilenlere göre, tan(GEC) aşağıdaki-
lerden hangisine eşittir?
B) -
A
20
G
13
D
E
E)
-
C
16
13
C) -
18
13

Geometri
İki Kat Açı FormülleriB
28. Şekilde ABML bir kare, BCDE ve FKLM ise birer dik-
dörtgendir.
A
A) 15
B
B) 30
(11) € 10
BY B
A Heady
bc=b
M
|BC| = |ME| = |EF| olduğuna göre m (DBK) = a kaç
derecedir?
C) 45
98
690
&
E
D
B
D) 60
K
F
E) 75
b
25+0
C(₂0) 25
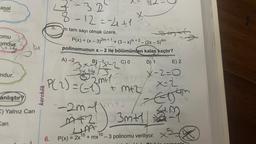
Geometri
İki Kat Açı Formülleriasal
omu 3
omdur.
mdur.
4₁
anlıştır?
C) Yalnız Can
Can
karekök
6.
3.2
x
8-12=-2₁+1 1/
x=
A)-²x-³¹-C0
B)
m tam sayı olmak üzere,
Latvalle
P(x) = (x - 3)2m + 1 + (3-x)m +2 - (2x - 5)4m
polinomunun x - 2 ile bölümünden kalan kaçtır?
D) 1
13₁
2ME1
P(2) = (-13m² = m+²/
t
P(x)
-2m-1m12
MFZ 3mtl
LIAA
= 2x¹0 + mx
2x15
2
10
+ mx¹0 - 3 polinomu veriliyor.
5A9
X-2=0
x=2
Zeytin
3m+1/3
x5-
E) 2
![11. SINIF - ORİJİNAL MATEMATİK
3.
A) 3 B) 5 C) 6
A
4
8 H
A) 10
O
8
D
B) 13 C) 15
D) 4√3 E) 5√2
B
Yukarıdaki verilere göre, çemberin yarıçapı kaç
cm'dir?
O merkezli
yarım çember
[EH] [CD]
|CH| = |HD|= 8 cm
|EH| = 4 cm
D) 17 E) 20
86](https://media.kunduz.com/media/question/seo/raw/20230314181935491603-4893649.jpg?w=256)
Geometri
İki Kat Açı Formülleri11. SINIF - ORİJİNAL MATEMATİK
3.
A) 3 B) 5 C) 6
A
4
8 H
A) 10
O
8
D
B) 13 C) 15
D) 4√3 E) 5√2
B
Yukarıdaki verilere göre, çemberin yarıçapı kaç
cm'dir?
O merkezli
yarım çember
[EH] [CD]
|CH| = |HD|= 8 cm
|EH| = 4 cm
D) 17 E) 20
86
Geometri
İki Kat Açı Formülleri3.
C
D
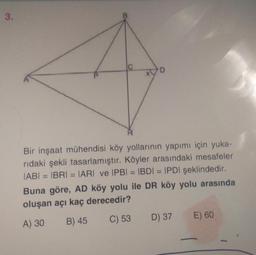
Bir inşaat mühendisi köy yollarının yapımı için yuka-
ridaki şekli tasarlamıştır. Köyler arasındaki mesafeler
IABI= IBRI = |ARI ve IPBI = IBDI = IPDI şeklindedir.
Buna göre, AD köy yolu ile DR köy yolu arasında
oluşan açı kaç derecedir?
A) 30
B) 45
C) 53
D) 37
E) 60
![ANIM TEST-3
4.
12
A) 12
+
B) 14
O
6
B
10
ABC ve CED dik üçgen,
BCEF dikdörtgen
[AF] [BC],
[DF] [CE]
GE |DC| = 10 birim
|CB| = 6 birim
|AB| = 12 birim
2x
m(DCE) = 2 m(CAB)
Buna göre, |DE| + |BF| toplamı kaç birimdir?
D) 16
C) 15
D
F
E) 18](https://media.kunduz.com/media/question/seo/raw/20230314091457828608-1229787.jpeg?w=256)
Geometri
İki Kat Açı FormülleriANIM TEST-3
4.
12
A) 12
+
B) 14
O
6
B
10
ABC ve CED dik üçgen,
BCEF dikdörtgen
[AF] [BC],
[DF] [CE]
GE |DC| = 10 birim
|CB| = 6 birim
|AB| = 12 birim
2x
m(DCE) = 2 m(CAB)
Buna göre, |DE| + |BF| toplamı kaç birimdir?
D) 16
C) 15
D
F
E) 18
