Kosinüs Teoremi Soruları

Geometri
Kosinüs Teoremi8
8.
Ø
a
B) -
5
5
13
D
cosa
C
Yukarıda kirişler dörtgeni verilmiştir. COS(180)
Buna göre, cosa kaçtır?
A) - 13
x²= 9+25-30casa
x= 16+36-48 Cose Sin
C) 13
2+0=180
7-18000
D)
5
13
33-30cosa = 52-48 sina
48 sind -30cos = 29
E)
7
13
Geometri
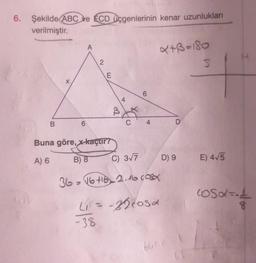
Kosinüs Teoremi6. Şekilde ABC ve ECD üçgenlerinin kenar uzunlukları
verilmiştir.
B
6
A
2
E
B
4
6
C 4
Buna göre, x-kaçtır?
A) 6
B) 8
C) 3√7
36-16 +162.16 cosa
(i = -22cosa
-38
661
4+3=180
D
D) 9
S
E) 4√5
H
CS4=
dünk eg
Geometri
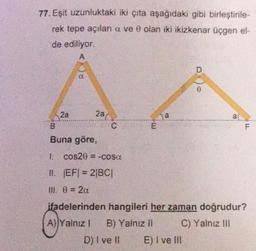
Kosinüs Teoremi77. Eşit uzunluktaki iki çıta aşağıdaki gibi birleştirile-
rek tepe açılar a ve 0 olan iki ikizkenar üçgen el-
de ediliyor.
A
2a
(()8
28(
C
B
Buna göre,
1. cos20 = -cosa
11. |EF| = 2|BC|
III 0 = 2a
W
a
D
E) I ve III
a
F
ifadelerinden hangileri her zaman doğrudur?
A)|Yalnız ! B) Yalnız II
C) Yalnız III
D) I ve Il
Geometri
Kosinüs Teoremibir evin önden görünüşü verilmiştir.
A)
D
Bir üst kata çıkaran merdiven ABC dik üçgeninin hipotenú-
sü üzerine yerleştirilmiştir.
H
C
m(CAB) = a, |AB| = b ve |BC| = a birimdir.
3.(a+b)=2-JAC
olduğuna/gare, sin2α kaçtır?
strza
B)
B
a
4
C)
5
D) 1/1/0
8) -/-

Geometri
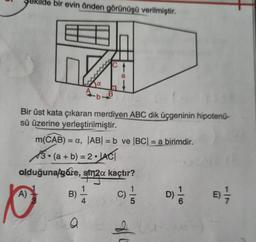
Kosinüs Teoremi3. Şekilde bir evin önden görünüşü verilmiştir.
Bir üst kata çıkaran merdiven ABC dik üçgeninin hipotenü-
sü üzerine yerleştirilmiştir.
m(CAB) = a, |AB| = b ve |BC| = a birimdir.
√3 (a + b) = 2 |AC|
olduğuna göre, sin2a kaçtır?
1
B) 1/24
3
A)
C)
1
5
2.sina.cosa
D)
E) 1/2

Geometri
Kosinüs Teoremi158
3.
B
6
4
30°
D
45°
D
5
sind
X
4
3m
8
cosa.
()
alt
niz.
C
M
ABC üçgen, 3IBDI = IDCI
m (BAD) = 30°, m (DAC) = 45°, IABI= 6 br
Yukarıda verilenlere göre, IACI = x değeri kaçtır?
A) 3√2 B) 6
C) 9
D) 12 E) 9√2
6.
B
Yukarı
ğu kad
A) 8
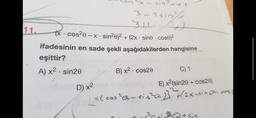
Geometri
Kosinüs Teoremi11.
3-3 sin
3.11-
→
(x cos²0-x sin²0)² + (2x sine cose)²
ifadesinin en sade şekli aşağıdakilerden hangisine
eşittir?
A) x² sin20
.
.
B) x² cos20
.
C) 1
D) x²
E) x² (sin20+ cos28)
[x ( cos³-sinta) + (2x.sina.co

Geometri
Kosinüs Teoremi√2.3√2 = √2
sin 60
B
derecedir?
Y
413 4√2
4√3
sinx
& sin + √2
E
sinxy
MODEL Y
D) 75 E) 90
2
A135° 12
-1/2
R6
B
olduğuna göre, R kaç br dir?
A) 2√2
To 10
Şekilde ABC üçgeni ve O
merkezli çevrel çemberi ve-
rilmiştir.
m(BAC) = 135°
|BC| = 12 br
B) 3√2 C) 4√2 D) 6√2 E) 8√2
1-D 2-B 3-D 4-D
TRIGONOMETRI

Geometri
Kosinüs Teoremi1.
M
IPRI = 3 birim, IPTI = 5 birim, IRSI = 4 birim,
11
ITSI = 2 birim ve cos(PRS) =
tür.
24
Şekildeki gibi P noktasından S noktasına
koşmakta olan köpeği, R noktasında ve T
noktasında bulunan iki kişi gözlemlemektedir.
Buna göre, T noktasındaki kişinin köpeği
takip ederken gözünün taradığı PTS açısının
kosinüsü kaçtır?
A2
9
20
B
5
7
20
PD ==
D)
3
10
EA
4

Geometri
Kosinüs Teoremi13-433
312
10.
33
+
10.413
240
olduğuna göre, |AB| cos A + |BC|
kaçtır?
A) 5
B
C
ABC üçgeninde IABI= 13 br, IACI = 12 br, IBCI= 10 br
B) 12
16.9
144 17
313.
C) 13
12
13
50 = 168 +144-2-13.12. COS A
D)
13
12
26
+36
cos C ifadesinin değeri
E) 10

Geometri
Kosinüs Teoremi8.
B
6
A
CA
ABC üçgeninde
m(BAC) > 90°
|AB| = 6 cm
|AC| = 4 cm
ABC üçgeninin alanı 3√15 cm² olduğuna göre,
|BC| kaç cm dir?
e A on
po
A) 12
B) 10
C) 9
D) 8
A (ABC) = 6. SMA = 3√15
12.JnA = 3√15
SMA = √15/4
E) T

Geometri
Kosinüs TeoremiAPOIEM
16.
işleminin sonucu aşağıdakiler
A) 2 44
B) 2 21
4
E
B 3√√
6
A) 1
14) C
A
a
3√√12
6
D
B) 3
sinu-sinb
olduğuna göre, |DC| kaçtır?
C) 1 D) √2 E) 225
C
C) 4
hangisidir?
15) A
ABC eşkenar
üçgendir.
|AE| = 6
|EB|
= 4
|ED| = 3√7
D) 5√2
Trigonometri
E) 6
16) A
-
Geometri
Kosinüs Teoremi2.
3+4
9-4-12.2
RU
B
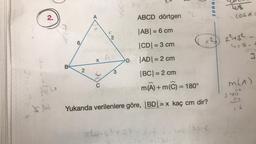
ABCD dörtgen
|AB| = 6 cm
|CD| = 3 cm
D |AD| = 2 cm
|BC| = 2 cm
m(A) +m(C) = 180°
Yukarıda verilenlere göre, |BD| = x kaç cm dir?
6
2
X
C
62
622
OS
3
12
X
xong 2 2.6.2. Cas 180-c
nuos
(osd:
2²432
418-8
1
M.(A)
140
24
Geometri
Kosinüs TeoremiA
C
i
L
Y
A
Y
I
N
L
A
R
1
10.
B
302 x=(33) oop snuğublo
50°
4√3
R
70%
u
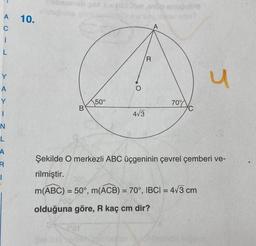
Şekilde O merkezli ABC üçgeninin çevrel çemberi ve-
rilmiştir.
m(ABC) = 50°, m(ACB) = 70°, IBCI= 4√3 cm
-
olduğuna göre, R kaç cm dir?
![C
at
204=24
36. Fatih Öğretmen, derste öğrencilerine bir geometrik
çizimin adımlarını şu şekilde vererek aşağıdaki soruyu
yöneltiyor.
by
●
.
●
A açısı geniş olan bir ABC üçgeni çiziniz.
[AC] kenarının orta noktasını D olarak
isimlendiriniz.
D noktasından AB doğrusuna çizilen dik doğrunun
AB doğrusunu kestiği noktayı E olarak
isimlendiriniz.
A) 10
|AB| = 9 cm, |AE| = 3 cm ve |DE| = 4 cm'dir.
Bu çizime göre [BC] kaç cm'dir?
Buna göre, Fatih Öğretmen'in söylediği adımları
doğru şekilde yapıp soruyu çözen İlkem'in vermesi
gereken cevap aşağıdakilerden hangisidir?
B) 12
73
C) 13
bar
2r
D) 15
E) 17
14](https://media.kunduz.com/media/question/seo/raw/20230211092757315891-4672229.jpg?w=256)
Geometri
Kosinüs TeoremiC
at
204=24
36. Fatih Öğretmen, derste öğrencilerine bir geometrik
çizimin adımlarını şu şekilde vererek aşağıdaki soruyu
yöneltiyor.
by
●
.
●
A açısı geniş olan bir ABC üçgeni çiziniz.
[AC] kenarının orta noktasını D olarak
isimlendiriniz.
D noktasından AB doğrusuna çizilen dik doğrunun
AB doğrusunu kestiği noktayı E olarak
isimlendiriniz.
A) 10
|AB| = 9 cm, |AE| = 3 cm ve |DE| = 4 cm'dir.
Bu çizime göre [BC] kaç cm'dir?
Buna göre, Fatih Öğretmen'in söylediği adımları
doğru şekilde yapıp soruyu çözen İlkem'in vermesi
gereken cevap aşağıdakilerden hangisidir?
B) 12
73
C) 13
bar
2r
D) 15
E) 17
14

Geometri
Kosinüs Teoremi2.
B
A)
2/3
D)
√3
2
A
6
Sina
8
Buna göre, cos(ABC) değeri kaçtır?
6
B)
1
C
3
Sinza
E)
10/2/3=
-
3
ABC üçgen
|BC| = 8 birim
|AC| = 6 birim
966.
m(BAC) = 2m (ABC)
29
C)
6. Sin 2a= 8 sina.
√√2
2
endemik
=sina -63
nza 74
5.
D
Bu
A)
