Kosinüs Teoremi Soruları
![2. ABC üçgen
|BD| = |DE| = 1
D
s
B
|BC| = 3
[DB] L [BC]
[BA] [AC]
m(ACB) = a
Yukarıda verilenlere göre, |AE| uzunluğunun a cinsin-
den eşiti aşağıdakilerden hangisidir?
A) na-2cos a
E
C) 3cos a -2sin a
A
LS
E) 3cot a - 2tan a
C
B) 3tan a - 2cot a
D) 2cos a-3sin a](https://media.kunduz.com/media/question/seo/raw/20230210152244587639-3882913.jpg?w=256)
Geometri
Kosinüs Teoremi2. ABC üçgen
|BD| = |DE| = 1
D
s
B
|BC| = 3
[DB] L [BC]
[BA] [AC]
m(ACB) = a
Yukarıda verilenlere göre, |AE| uzunluğunun a cinsin-
den eşiti aşağıdakilerden hangisidir?
A) na-2cos a
E
C) 3cos a -2sin a
A
LS
E) 3cot a - 2tan a
C
B) 3tan a - 2cot a
D) 2cos a-3sin a

Geometri
Kosinüs TeoremiBir sokak performans sanatçısı dörtgen biçimindeki camla
üzerine resimler çizmektedir. Sanatçı, ikizkenar dik üçgen
şeklinde tasarladığı boyutları farklı iki kelebek kanadını, dil
açılara ait köşeler üst üste gelecek biçimde cam üzerine
çizmektedir.
by b
Daba
S2
524
45°
6√2 cm
to
ob
-7,5
a² tb²
2ab.c
72
Dörtgen biçimindeki camın bir kenar uzunluğu 6√2 cm
ve kanatların birbiriyle yaptığı açılardan biri 45° olduğun
göre, camın alanı kaç cm²'dir?
A) 36
B) 48
C) 60
D) 72
E) 96
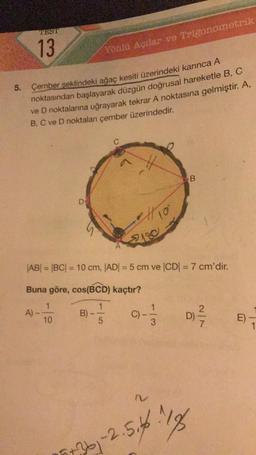
Geometri
Kosinüs Teoremi5.
TEST
13
A)
Çember şeklindeki ağaç kesiti üzerindeki karınca A
noktasından başlayarak düzgün doğrusal hareketle B, C
ve D noktalarına uğrayarak tekrar A noktasına gelmiştir. A,
B, C ve D noktaları çember üzerindedir.
Yönlü Açılar ve Trigonometrik
10
B)
A
tio
|AB| = |BC| = 10 cm, |AD| = 5 cm ve |CD| = 7 cm'dir.
Buna göre, cos(BCD) kaçtır?
2180
(C) --
3
B
-2.5.4.18
77361-2.5.66
D)
E)
1
![YARIYIL TATİL ÖDEVİ
16.
Yukandaki verilenlere göre, ABCD dörtgeninin
alanı kaç cm² dir?
A) 9(2 + √5)
17.
|AB| = 3 cm
|CD] = 7 cm
|BC| = 6 cm
|AD| = 4 cm
m(BAD) = 90*
B) 6(1 + √6)
D) 3(1+√3)
C) 5(2 + √7)
E) 2(3+√3)](https://media.kunduz.com/media/question/seo/raw/20230209153637467290-1370005.jpeg?w=256)
Geometri
Kosinüs TeoremiYARIYIL TATİL ÖDEVİ
16.
Yukandaki verilenlere göre, ABCD dörtgeninin
alanı kaç cm² dir?
A) 9(2 + √5)
17.
|AB| = 3 cm
|CD] = 7 cm
|BC| = 6 cm
|AD| = 4 cm
m(BAD) = 90*
B) 6(1 + √6)
D) 3(1+√3)
C) 5(2 + √7)
E) 2(3+√3)
![20.
M
K
A)
R
12
13
T
A
B
C
MNPR karesinin P ve R noktaları, S ve T nokta-
larına uzatılarak şekildeki MNST dikdörtgeni oluş-
turuluyor. Sonra bu dikdörtgen şeklin ST kenarı-
na C noktasında teğet, çapı PR uzunluğunda ve
merkezi B noktası olan bir çember çizilip makas ile
kesilerek atılıyor.
B)
N
Daha sonra kalan kısım, çembere A noktasında
teğet olan [NK] doğrultusunda kesilerek şekildeki
sarı renkli KMN üçgeni elde ediliyor.
P
Buna göre, KNM açısının kosinüs değeri kaç-
tır?
S
C)
D) 533
13
25](https://media.kunduz.com/media/question/seo/raw/20230209135832969899-594248.jpg?w=256)
Geometri
Kosinüs Teoremi20.
M
K
A)
R
12
13
T
A
B
C
MNPR karesinin P ve R noktaları, S ve T nokta-
larına uzatılarak şekildeki MNST dikdörtgeni oluş-
turuluyor. Sonra bu dikdörtgen şeklin ST kenarı-
na C noktasında teğet, çapı PR uzunluğunda ve
merkezi B noktası olan bir çember çizilip makas ile
kesilerek atılıyor.
B)
N
Daha sonra kalan kısım, çembere A noktasında
teğet olan [NK] doğrultusunda kesilerek şekildeki
sarı renkli KMN üçgeni elde ediliyor.
P
Buna göre, KNM açısının kosinüs değeri kaç-
tır?
S
C)
D) 533
13
25

Geometri
Kosinüs TeoremiD
b
3. Şekilde bir evin önden görünüşü verilmiştir.
2 Sina Sob
Bir üst kata çıkaran merdiven ABC dik üçgeninin hipotenü-
sü üzerine yerleştirilmiştir.
m(CAB) = a, |AB| = b ve |BC| = a birimdir.
√3 (a + b) = 2 ·|AC|
olduğuna göre, sin2α kaçtır?
1
C)
3
A)
●
1
B) -—-
4
53
2
KARMA
(9+b)53
2
√3 (a+b =(2²+6²) 2
a² tb²
D) 1/2
6
92
atb
a² +5²
E) --

Geometri
Kosinüs TeoremiMatematik Kulübü
12. Başlangıç noktası O olan bir dik koordinat düzlemin.
de A(-1, 3) ve B(2, -1) noktaları veriliyor.
CON NOS
Buna göre, AOB üçgeninde O açısının ölçüsü
kaç derecedir?
(Kosinüs teoremini kullanabilirsiniz.)
A) 105 B) 120 C) 135
9160 anua
Stoshopob
D) 140
E) 150
3.
Geometri
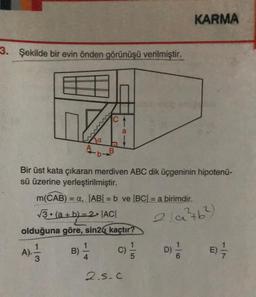
Kosinüs Teoremi3. Şekilde bir evin önden görünüşü verilmiştir.
Lozn
a
A
-b-B
O
4R1
a
Bir üst kata çıkaran merdiven ABC dik üçgeninin hipotenü-
sü üzerine yerleştirilmiştir.
m(CAB) = a, |AB| = b ve |BC| = a birimdir.
√3 • (a+b)=2•|AC|
olduğuna göre, sin2 kaçtır?
A), 1/14
B) -1/14
C) 1/1/2
15
2.5. C
KARMA
2(a²46²)
16
D) 1/1/0
E) -—-/-

Geometri
Kosinüs Teoremix-5
21
2
8. Bir ABC üçgeninde
a = 6 br
sino
A+B+C =18
sin(B+C)=-
98
+ sinA=
A) 4
4
5
(B)
sinc =
15
B
olduğuna göre bu üçgenin çevrel çemberinin yar
çapı kaç br dir?rheq ases suu
C)
sk
7/2
3
(3k
672
D)
13
Sayfa:66
E) 3
12. A
1
SU

Geometri
Kosinüs TeoremiK L
A
B
X
2
A) - -/B)
3
C
M N R
D
Kestaneli
E
80 cm
Boyu 80 cm ve eni 60 cm olan üstü dikdörtgen olan
pasta, parti yapacak olan 4 arkadaşa isteklerine göre
şekildeki gibi eşit bölünüyor.
60 cm
Arkadaşlarından biri partiye gelemediği için kestaneli
kısmı Can'a verip diğer kısım |KD| boyunca paylaşı-
yorlar.
Buna göre, oluşan KPC açısının kosinüs değeri
kaçtır?
√3 C)-1/2/ D) 1/13
√√3
3
E)
√2
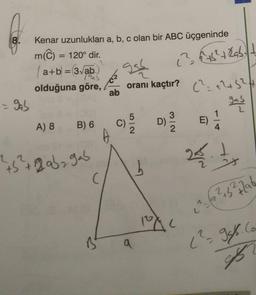
Geometri
Kosinüs Teoremi8.
= gab
Kenar uzunlukları a, b, c olan bir ABC üçgeninde
m(C) = 120° dir.
(a+b = 3√ab
olduğuna göre,
A) 8
B) 6
+5² + 2ab₂ gab
C
Bt
ab
A
gad
oranı kaçtır?
C)
5
2
b
2
(3²= {²+6² + 2ab²
D)
3
2
100L
E)
1
²45 ²4
gase
25.1
1²+5² 796
² gab.Com
957

Geometri
Kosinüs Teoremimit C
a
5√2
2.
64
F
A
4
D
35
20
2
8/0
64
C
5
a
B
ABCD yamuk
IADI= 4 br
|ABI = 8 br
IBC| = 5 br
IDCI = 2 br
m(ABC) = c
Yukarıda verilenlere göre, cosa'nın değeri kaç-
tır?
A) 23/10 B) // C) 17/0
D) 3/10
4
E) //
5. A
6.

Geometri
Kosinüs Teoremi33.
2,1
K
P
Şekil 1
2
A
2,1
K
B) 160
37
P
20
C) 150
X
53
Şekil 2
37
1,2
2,1 metre yüksekliğindeki yere dik durumdaki duvarın P
köşesine değecek biçimde yerleştirilen kalınlığı önemsiz
2 metre uzunluğundaki bir kalasın diğer ucuna ip bağla-
niyor.
A
1,6
İp, duvarın K köşesindeki makaradan geçirilerek Şekil 1
deki konumda tutuluyor.
Daha sonra kalasın A ucu yerden 1,6 metre yükseğe
çıkıncaya kadar ip çekilerek kalas, Şekil 2 deki konuma
getiriliyor.
Buna göre, Şekil 2 de ipin AK parçasının uzunluğu
kaç cm dir?
A) 170
D) 140
E) 130

Geometri
Kosinüs Teoremi31. İkizkenar üçgen biçimindeki eş kenarları 10 birim olan
mavi renkli kâğıt ile eş kenarları 6 birim olan turuncu
renkli kâğıt Şekil-l'de verilmiştir.
B
10.
A
10
B) 9
Şekil-l
6
CBX
6
C) 11 D) 12
Şekil-II
Bu kâğıtların eş olmayan kenarları birer köşelerinden
birleştirilerek bir d doğrusu ile Şekil-ll'deki gibi çakıştı-
rılmıştır.
d
Taban açıları 45° den küçük olan kâğıtların AB ve CD
kenarlarını taşıyan doğruları arasındaki geniş açı 120°dir.
Buna göre, 'A ile C noktaları arası uzaklık kaç birim-
dir?
A) 8
D
E) 14
Hent
14
ABC
Kat
Şek
A
3
K
14
E
B
A
Geometri
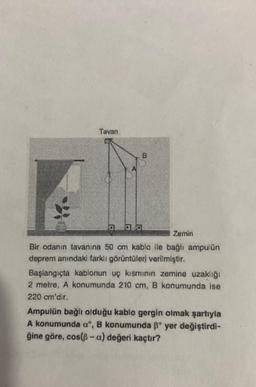
Kosinüs Teoremi000
Bir odanın tavanına 50 cm kablo ile bağlı ampulün
deprem anındaki farklı görüntüleri verilmiştir.
Başlangıçta kablonun uç kısmının zemine uzaklığı
2 metre, A konumunda 210 cm, B konumunda ise
220 cm'dir.
Ampulün bağlı olduğu kablo gergin olmak şartıyla
A konumunda o", B konumunda º yer değiştirdi-
ğine göre, cos(-a) değeri kaçtır?
Geometri
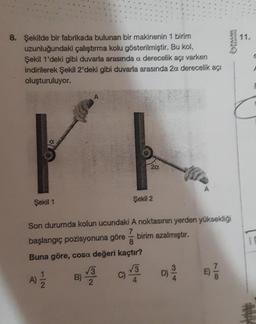
Kosinüs Teoremi8. Şekilde bir fabrikada bulunan bir makinenin 1 birim
uzunluğundaki çalıştırma kolu gösterilmiştir. Bu kol,
Şekil 1'deki gibi duvarla arasında a derecelik açı varken
indirilerek Şekil 2'deki gibi duvarla arasında 20. derecelik açı
oluşturuluyor.
Şekil 1
B)
√3
2
20.
Son durumda kolun ucundaki A noktasının yerden yüksekliği
7
başlangıç pozisyonuna göre
Buna göre, cosa değeri kaçtır?
√√3
C)
Şekil 2
birim azalmıştır.
SATVER
D) 2/20
TARSIAKA
11.
10
