Trigonometrik Denklemler Soruları

Geometri
Trigonometrik Denklemler14.
1-2sina cosa
sin²a-cos²a 2
olduğuna göre, tana ifadesinin değeri kaç olabi-
lir?
12/12/12
2- Usina. Cosd = Sin ²α = (1 - sinzα)
2 - Usind.casd = 2 sin ²α-1
A).
3
28in 2d+u.sind. casa = 3
2sina (sind + 2 cosa 7 = 3
D) 2
12
E) 3

Geometri
Trigonometrik DenklemlerTX
ÖRNEK: 28
1 tanx
1+cotx
+
1 tanx 1 cotx
ifadesinin en sade şekli aşağıdakilerden hangisidir?
A) sinx
B) secx
C) cosx
D) cosecx
Çözüm
ÖRNEK: 29
COSX
1sinx
Trigonometri
cotx
1+cosecx
E) 0
J
ifadesinin en sade şekli aşağıdakilerden hangisidir?
2
A) 2secx B) secx C) cosecx D) sinx
E) 1+tanx

Geometri
Trigonometrik Denklemler1. ÜNİTE
200
3π
< ³7 olduğuna göre,
2
180
8. <a<ß<
1. sina > sinß
II. cosa > cosß
III. tana > sina
ifadelerinden hangilerinin değeri pozitiftir?
B) Yalnız II
A) Yalnız I
D) II ve III
E) I ve III
C) I ve II

Geometri
Trigonometrik Denklemler4.
D
360
sin(+x) + cos(2 - x)
240
3r
cost cost Stan 2
21050
D) -sinx
-X
11. SINIF
MATEMATİK
z
cosx tố án
tan cotx cost
Sinx
ifadesinin eşiti aşağıdakilerden hangisidir?
A) -2cosx
B) 0
C) 2
E) 2sinx
sinx
cost

Geometri
Trigonometrik Denklemler5.
mx(cos²x
sina teosa
(in), (may-sa)
Sirkesina.co.
21
SAX
aca
A) -
√3
2
D) -
√3
2
1
330°
a
B)
Şekildeki birim çemberde verilen A(m, n) noktası-
na göre m.n kaçtır?
√√3
3
11. SINIF
MATEMATİK
6. x=-2930° olduğuna göre,
I.sinx
||. cosx
III. tanx + cotx
Syam
nin
1
A (m,n)
X
E) -
721
morg
√√3
√3

Geometri
Trigonometrik DenklemlerA
28.
niz
D) Ivett
2.sin (54°) tan (18°) +-
B) Yalnız t
A) cosec(36°)
D) sec(18°)
-E), Ive
cos (18)
cos (36)
ifadesinin eşiti aşağıdakilerden hangisidir?
C) Yalnız III
B) cos(18°)
C) 2sin(36°)
E) 2tan(54°)
SUDH
m
M

Geometri
Trigonometrik Denklemlerno S
5√3
3
A).
A
B
D
C
ABC eşkenar üçgen, |BD| = 2 |DC|, m (DAC) = x
tir.
D)
1 do (20x)
Yukarıdaki verilere göre, tanx kaçtır?
√√3
3√3
5
X
B)
1-31/12/2
-
621-3 24
5
078 197
5√5
3
C)
198
3√5
E)
5
toletat
tax
![k
AE
ÖSYM
Örnek: 5
O merkezli birim çember, A, B çember üzerinde, A= Ox ekseni,
[BD]L[OA), m(BOD)=a
AY
O
a
B
D₁
cost
C) √3
A
4X
Şekildeki O merkezli birim çemberde cosa= |AB| olduğuna
göre, |AB| kaç birimdir?
A) √3+2
B) √3+1
Topel
D) √3-1
E) √3-2
(1996/ÖYS)
ABCI
m(LE
Yuk
A)](https://media.kunduz.com/media/question/seo/raw/20230301200158773330-383553.jpeg?w=256)
Geometri
Trigonometrik Denklemlerk
AE
ÖSYM
Örnek: 5
O merkezli birim çember, A, B çember üzerinde, A= Ox ekseni,
[BD]L[OA), m(BOD)=a
AY
O
a
B
D₁
cost
C) √3
A
4X
Şekildeki O merkezli birim çemberde cosa= |AB| olduğuna
göre, |AB| kaç birimdir?
A) √3+2
B) √3+1
Topel
D) √3-1
E) √3-2
(1996/ÖYS)
ABCI
m(LE
Yuk
A)

Geometri
Trigonometrik Denklemler34cht ~(-+*)
²1-ORNEK: 27
11sinx
COSX
COSX
1-+sinx
ifadesinin en sade şekli aşağıdakilerden hangisidir?
E) cosecx
A) sinx B) cosx
D) 2secx
C) 2cosecx
Çözüm
+
cos x-sin x+5
2pos x+sin
ifadesinin en sade
Çözüm
![G
A) 34
D
8)
B) 36
E
K
(2)
A
F B
ABCD paralelkenar, [AC] köşegen, [DA]//[EF]
[AB]//[GH], Alan (GKED)=8 birimkare
Alan (CKH)=2 birimkare
Yukarıdaki verilere göre, Alan (ABCD) kaç birim-
karedir?
C
C) 38 D) 40
H
E) 48](https://media.kunduz.com/media/question/seo/raw/20230301190854284804-2008582.jpg?w=256)
Geometri
Trigonometrik DenklemlerG
A) 34
D
8)
B) 36
E
K
(2)
A
F B
ABCD paralelkenar, [AC] köşegen, [DA]//[EF]
[AB]//[GH], Alan (GKED)=8 birimkare
Alan (CKH)=2 birimkare
Yukarıdaki verilere göre, Alan (ABCD) kaç birim-
karedir?
C
C) 38 D) 40
H
E) 48

Geometri
Trigonometrik Denklemlerfest 05
değeri
C) 645
Trigonometrik Özdeşlikler - II
Geliştir
4.
1
1+tanx
1
1+cotx
ifadesinin en sade şekli aşağıdakiler-
den hangisidir?
A) sinx
C) 1
E) 2sinx
B) cosx
D) sinx + cosx
08/+Co+++an+ cottan
1.

Geometri
Trigonometrik Denklemlersi (80-30)
5130
4-1/2
3) nok-
kilerden hangisidir?
2√2
√2
3√2
5
2
5
six.cosur + silicosx
A)
O
B)
C)
=
on
19
P)
7√2
10
+
4√2
LO
E)
2√2
5
752
10
cos5x cos3x-sin5x sin3x = sin2x
denkleminin en küçük pozitif kökü kaç derecedir?
A) 6
B) 8
C) 9
D) 12
E) 15
15-
Analitik düzlemde A(a, 5) noktasının 2x + 6y + b = 0 doğ-
rusuna göre simetriği A'(-2,-7) noktasıdır.
Buna göre, a + b toplamı kaçtır?

Geometri
Trigonometrik DenklemlerA
17. ABCD ve BEFK birer karedir.
3
4
D
A) 2
A
y
IX
teme AYT
B)
A
4√2
4
2
C
2sts
|AB| = 2 |BE|
m(ADB) = y, m(FDC) = X
K
NOVE
2
olduğuna göre, cot(x + y) kaçtır?
1
B
2
2√2
F
2
16.2
brsle
32 + 8 =√40 25
E
C) 3
D)
(1910süstemio R
(4√√2₂) + (2√2) ² (²
4.2
A
L
E)
19. a ve b
tay+tay rel
1-day-tay 2
2|5
lin
X-
e
Igen 20
oldu
A
A) 12
l

Geometri
Trigonometrik Denklemler81
B
D
A
A) 5 coseca + 8 seca
C) 5 cosa + 8 sina
5 m
Şekilde açılır kapanır kapakları olan bir kanalın
üstten görünüşü gösterilmiştir.
E
Bu kapaklar açıldığında A ucu C noktasına, B ucu
D noktasına gelmektedir. CDE bir dik üçgen oldu-
ğuna göre |CD| nin a cinsinden eşiti aşağıdaki-
lerden hangisidir?
B) 8 cosa + 5 sina
D) 8 coseca + 5 seca
E) 8 sind - 5 cosa
![7-20
50-20160
6C1610
asch
farklı kökü
4
51
2.18
F
890
SCH2-1852
she
G
arklı kökü
iny
E) 8
360
3-0
1801360 2
IT
klı kökü
4) A
E) 6
E) 1
APOIEMI
7.
6.
3 x
8.
59
JA DA
6x=
50
36
2+sinx =
TU
A) =
57
5) D
12
(ny-2) (amn
B)
5/6
TU
+27
sin
2.2-smx-cosx
MY
2 sin2x-cosx
t
B) 4
516
→ 227
von7
olduğuna göre, aşağıdakilerden hangisi bu
denkleminin bir köküdür?
sm@=€
C)
eos x
3
2π
- 1
1 C
36
36
C) 6
57
36
370
36
150
361
+ zen
31
pau
3π
2
viny
omnibs no imalined
jugnion,
26
36 3
44227 3:30
360 12
R
6) D
7) C
x = 180-3y +-2711
asmx
denkleminin [0,2π] aralığında kaç farklı kökü
vardır?
A) 2
D) 700 E) 8
COSX =oSx
E)
25
(inx-2) (smy-3)
günob enimild
090
36 36
un
7T
4
sbrigibiles (*)
290
34
957
86
sin (2m-30°) = cosm
denklemini sağlayan [0°,180°] aralığındaki m
değerlerinin toplamı kaç derecedir?
A) 360°
B) 320° C) 280° D) 200°
E) 120°
8) B
125
―](https://media.kunduz.com/media/question/seo/raw/20230301171104201802-3486818.jpeg?w=256)
Geometri
Trigonometrik Denklemler7-20
50-20160
6C1610
asch
farklı kökü
4
51
2.18
F
890
SCH2-1852
she
G
arklı kökü
iny
E) 8
360
3-0
1801360 2
IT
klı kökü
4) A
E) 6
E) 1
APOIEMI
7.
6.
3 x
8.
59
JA DA
6x=
50
36
2+sinx =
TU
A) =
57
5) D
12
(ny-2) (amn
B)
5/6
TU
+27
sin
2.2-smx-cosx
MY
2 sin2x-cosx
t
B) 4
516
→ 227
von7
olduğuna göre, aşağıdakilerden hangisi bu
denkleminin bir köküdür?
sm@=€
C)
eos x
3
2π
- 1
1 C
36
36
C) 6
57
36
370
36
150
361
+ zen
31
pau
3π
2
viny
omnibs no imalined
jugnion,
26
36 3
44227 3:30
360 12
R
6) D
7) C
x = 180-3y +-2711
asmx
denkleminin [0,2π] aralığında kaç farklı kökü
vardır?
A) 2
D) 700 E) 8
COSX =oSx
E)
25
(inx-2) (smy-3)
günob enimild
090
36 36
un
7T
4
sbrigibiles (*)
290
34
957
86
sin (2m-30°) = cosm
denklemini sağlayan [0°,180°] aralığındaki m
değerlerinin toplamı kaç derecedir?
A) 360°
B) 320° C) 280° D) 200°
E) 120°
8) B
125
―
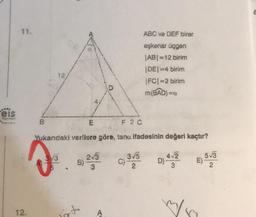
Geometri
Trigonometrik Denklemler***D
s
11.
B
12.
12,
F 2 C
Yukarıdaki verilere göre, tano ifadesinin değeri kaçtır?
0₁
d
E
B)
2√3
3
*
ABC ve DEF birer
eşkenar üçgen
|AB| =12 birim
|DE|=4 birim
|FC| =2 birim
m(BAD)=a
C)
3√5 D) 4√2
2
3
E) 5-√3
2
28
E
