Üçgende İç ve Dış Açıortay Soruları
Geometri
Üçgende İç ve Dış AçıortayDik Üçgen
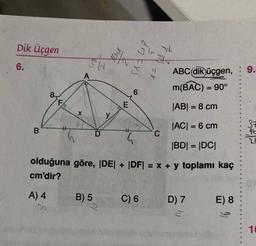
6.
B
8
FIN
ABC (dik)üçgen, : 9.
m(BAC) = 90°
|AB| = 8 cm
|AC| = 6 cm
|BD| = |DC|
olduğuna göre, |DE| + |DF| = x + y toplamı kaç
cm'dir?
A) 4
X
B) 5
10%
D
E
en Fys
7 h =
C) 6
C
D) 7
E) 8
37
10

Geometri
Üçgende İç ve Dış Açıortay35.
B
Araç kontrolü için kapı girişinde bulunan sarı çubuk ok
yönünde kalkınca araçlar geçebiliyor. Dik üçgen biçimindeki
bir yapının ağırlık merkezine sabitlenmiş sarı çubuğun
GA kısmının uzunluğu 60 cm'dir. Araç geçerken çubuğun
A noktası üçgen yapının B köşesi ile çakışmaktadır.
A) 180
A
Buna göre, çubuğun monte edildiği üçgen yapının
hipotenüsünün uzunluğu kaç cm'dir?
B) 160
C) 120 D) 100 E) 90
3
![D
1.
Süvari Mahallesine ait ABC üçgeni şeklindeki çocuk parkı
şekildeki gibidir.
B
135°
D
E
30°
Parkın B köşesinde bulunan Banu [AB] ve [BC] kenarına
eşit uzaklıkta olacak şekilde yürümeye başlıyor ve [AC]
kenarı üzerindeki D noktasında duruyor. Daha sonra D
noktasından başlayarak [BC] üzerindeki E noktasına
geliyor.
m(BAC) = 135°, m (ACB) = 30°
[DE] [BC] ve |DC| = 60 metre olduğuna göre, |AD|
kaç metredir?
A) 30√2 B) 30√3 C) 60
D) 30√5 E) 30√6
3.](https://media.kunduz.com/media/question/seo/raw/20230322135808322037-5253461.jpg?w=256)
Geometri
Üçgende İç ve Dış AçıortayD
1.
Süvari Mahallesine ait ABC üçgeni şeklindeki çocuk parkı
şekildeki gibidir.
B
135°
D
E
30°
Parkın B köşesinde bulunan Banu [AB] ve [BC] kenarına
eşit uzaklıkta olacak şekilde yürümeye başlıyor ve [AC]
kenarı üzerindeki D noktasında duruyor. Daha sonra D
noktasından başlayarak [BC] üzerindeki E noktasına
geliyor.
m(BAC) = 135°, m (ACB) = 30°
[DE] [BC] ve |DC| = 60 metre olduğuna göre, |AD|
kaç metredir?
A) 30√2 B) 30√3 C) 60
D) 30√5 E) 30√6
3.
![IMCI ELEMANLAR
8.
A
B
K**
19
D
B) 20
2
E
olduğuna göre, Çevre(DEC) kaç cm'dir?
A) 18
C) 24
19 getm
Kolay-Orta
sv.
=kJ
h2=9+!
a+b
2
ACABCD)=h₂²
Awa
x.(mt) = Ly
ACCIATO
JUROS
[AB] L [BC]
m(BEA) = m(AED)
m(DCA) = m(ACB)
|BC| = 12 cm
Orta
Orta-Zor
D) 30
Zor
E) 28](https://media.kunduz.com/media/question/seo/raw/20230322160524859267-4764869.jpeg?w=256)
Geometri
Üçgende İç ve Dış AçıortayIMCI ELEMANLAR
8.
A
B
K**
19
D
B) 20
2
E
olduğuna göre, Çevre(DEC) kaç cm'dir?
A) 18
C) 24
19 getm
Kolay-Orta
sv.
=kJ
h2=9+!
a+b
2
ACABCD)=h₂²
Awa
x.(mt) = Ly
ACCIATO
JUROS
[AB] L [BC]
m(BEA) = m(AED)
m(DCA) = m(ACB)
|BC| = 12 cm
Orta
Orta-Zor
D) 30
Zor
E) 28
![20.
A
Şekil 1'deki ABC dik üçgeni biçimli kartonda AC L BC.
|BD| = 5 br ve DC = 4 br'dir. Bu karton [AD] boyun-
ca katlandığında C köşesi [AB] üzerindeki K noktasıyla
çakışarak Şekil 2 oluşuyor. Sonra Şekil 2 [BE] boyun-
ca katlanıyor ve D köşesi [AB] üzerindeki N noktasıyla
çakışarak Şekil 3 oluşuyor.
A
B 5 D 4 C B
Şekil 1
Buna göre, Şekil 3'te
A) 3
5
B) 2
K
D
Şekil 2
AE
NE
C)
E
9
A
B
Z
oranı kaçtır?
Şekil 3
D) 2
LU
E
0055](https://media.kunduz.com/media/question/seo/raw/20230322152937601744-2447221.jpg?w=256)
Geometri
Üçgende İç ve Dış Açıortay20.
A
Şekil 1'deki ABC dik üçgeni biçimli kartonda AC L BC.
|BD| = 5 br ve DC = 4 br'dir. Bu karton [AD] boyun-
ca katlandığında C köşesi [AB] üzerindeki K noktasıyla
çakışarak Şekil 2 oluşuyor. Sonra Şekil 2 [BE] boyun-
ca katlanıyor ve D köşesi [AB] üzerindeki N noktasıyla
çakışarak Şekil 3 oluşuyor.
A
B 5 D 4 C B
Şekil 1
Buna göre, Şekil 3'te
A) 3
5
B) 2
K
D
Şekil 2
AE
NE
C)
E
9
A
B
Z
oranı kaçtır?
Şekil 3
D) 2
LU
E
0055

Geometri
Üçgende İç ve Dış Açıortay25. Dik koordinat düzleminde, köşeleri A(-12, 6), B(12,
6) ve C noktaları olan ABC üçgeninin açıortayları ori-
jinde kesişmektedir.
Buna göre, C noktasının koordinatları toplamı
kaçtır?
A) -8
-12
B) -9 C) -10 D) -11 E)-12
B
12
![beri
7.
A
8
B
03 D +
3
B) 2/2
x2
C
anol id sorunusu mo
Yukarıdaki verilere göre, IDCI = x kaç cm dir?
A) 1
C) 2
E) 3
UB)
O çemberin merkezi
m (ABO) = m (OBD)
[BD]1[OC]
IODI=3 cm
IABI= 8 cm
D)
5
2
T (8)
8 (A](https://media.kunduz.com/media/question/seo/raw/20230322112652306417-2007532.jpg?w=256)
Geometri
Üçgende İç ve Dış Açıortayberi
7.
A
8
B
03 D +
3
B) 2/2
x2
C
anol id sorunusu mo
Yukarıdaki verilere göre, IDCI = x kaç cm dir?
A) 1
C) 2
E) 3
UB)
O çemberin merkezi
m (ABO) = m (OBD)
[BD]1[OC]
IODI=3 cm
IABI= 8 cm
D)
5
2
T (8)
8 (A
![+
birim
rim
çem-
dir?
E) 6
eis
eis
eis
eis
eis
eis
Yayınlan
eis
cis
eis
eis
eis
eis
6.
5
A) 45
G
B
B) 48
C) 51 D) 54
CF
A) 1 B) 1,5 C) 2
C
Oº
C
E) 57
A
[AC]L[BC], |AC| =5 birim, |BC| =12 birim
Yukarıdaki verilere göre, ABC üçgeninin iç teğet
çemberinin yarıçapı kaç birimdir?
E
D C
D) 2,5 E) 3](https://media.kunduz.com/media/question/seo/raw/20230322092624244380-5341570.jpg?w=256)
Geometri
Üçgende İç ve Dış Açıortay+
birim
rim
çem-
dir?
E) 6
eis
eis
eis
eis
eis
eis
Yayınlan
eis
cis
eis
eis
eis
eis
6.
5
A) 45
G
B
B) 48
C) 51 D) 54
CF
A) 1 B) 1,5 C) 2
C
Oº
C
E) 57
A
[AC]L[BC], |AC| =5 birim, |BC| =12 birim
Yukarıdaki verilere göre, ABC üçgeninin iç teğet
çemberinin yarıçapı kaç birimdir?
E
D C
D) 2,5 E) 3
![I noktası
ABC üçgeninin
iç teğet
çemberinin merkezi
[AB] // [ID]
[AC] // [IE]
|BD|=5 cm
B 5 D
E 7 C
|DE|=8 cm, |EC| =7 cm olduğuna göre, ABC üçge-
ninin çevresi kaç cm dir?
B) 35
C) 40
A) 30
8
D) 45
E) 50](https://media.kunduz.com/media/question/seo/raw/20230322100246038324-4827993.jpg?w=256)
Geometri
Üçgende İç ve Dış AçıortayI noktası
ABC üçgeninin
iç teğet
çemberinin merkezi
[AB] // [ID]
[AC] // [IE]
|BD|=5 cm
B 5 D
E 7 C
|DE|=8 cm, |EC| =7 cm olduğuna göre, ABC üçge-
ninin çevresi kaç cm dir?
B) 35
C) 40
A) 30
8
D) 45
E) 50
![Yukarıda verilenlere göre, |EC| = x kaç cm dir?
22.
B
A
xy
K
2
2
NED
f
E
x-1
C
LOC
20+1+
ABC dik üçgen
[BE] açıortay
[AB] 1 [AC]
[AD] 1 [BC]
|AE| = 4 br
|KD| = 2 br
Yukarıda verilenlere göre, |AB| = x kaç brdir?
4+16](https://media.kunduz.com/media/question/seo/raw/20230322094348672561-4808287.jpeg?w=256)
Geometri
Üçgende İç ve Dış AçıortayYukarıda verilenlere göre, |EC| = x kaç cm dir?
22.
B
A
xy
K
2
2
NED
f
E
x-1
C
LOC
20+1+
ABC dik üçgen
[BE] açıortay
[AB] 1 [AC]
[AD] 1 [BC]
|AE| = 4 br
|KD| = 2 br
Yukarıda verilenlere göre, |AB| = x kaç brdir?
4+16
![7.
Düzlemde bir ABC üçgeninde m (ABC) = 90% dir.
A köşesinden çizilen iç açıortay
[BC] kenarını D noktasında kesiyor.
IBDI = 3 cm ve IDCI= 5 cm olduğuna göre,
IACI kaç cm dir?
A) 6
B) 8
C) 10
D) 12
E) 14
X
3D 50](https://media.kunduz.com/media/question/seo/raw/20230322090359111390-4628009.jpeg?w=256)
Geometri
Üçgende İç ve Dış Açıortay7.
Düzlemde bir ABC üçgeninde m (ABC) = 90% dir.
A köşesinden çizilen iç açıortay
[BC] kenarını D noktasında kesiyor.
IBDI = 3 cm ve IDCI= 5 cm olduğuna göre,
IACI kaç cm dir?
A) 6
B) 8
C) 10
D) 12
E) 14
X
3D 50

Geometri
Üçgende İç ve Dış AçıortayDeneme 9
Birbirine eş otuzbeş tane eşkenar üçgen şeklindeki puzzle
ile oluşan yapı yukarıdaki gibidir.
P ile A arasındaki en kısa uzaklık 4√31 br dir.
P noktasından harekete başlayan karınca kırmızı
çizgiler üzerinde ilerlemek şartıyla en az kaç birimle A
noktasına ulaşır?
A) 20
B) 22
C) 24
D) 28
35. Üst yüzeyi
konulmus
konumda
kenarları
E) 32
Bu örtü
çekildiğ
örtünür
Alper
![kare
4.
B
12
H
H
2k D
E
C
ABC üçgeninde her a
L) Bi
[AD] açıortay
|BH| = |HE|
|BD|
|DC|
|AB| = 12 br
=
S 13
2²33
332
D) 3
kreap
3k
509
78-3x Yukarıda verilenlere göre, |EC| kaç br'dir? xita
A) 8 B) 6 C) 4
E) 2](https://media.kunduz.com/media/question/seo/raw/20230322080708776280-5323242.jpg?w=256)
Geometri
Üçgende İç ve Dış Açıortaykare
4.
B
12
H
H
2k D
E
C
ABC üçgeninde her a
L) Bi
[AD] açıortay
|BH| = |HE|
|BD|
|DC|
|AB| = 12 br
=
S 13
2²33
332
D) 3
kreap
3k
509
78-3x Yukarıda verilenlere göre, |EC| kaç br'dir? xita
A) 8 B) 6 C) 4
E) 2
![B
E
G
B) 4
3√3
CE
Şekil 1
Şekil 2
Şekil 1'deki ABC dik üçgeni biçimli kâğıtta BA I AC ve G
ağırlık merkezidir. Bu kâğıt [DE] boyunca katlandığında
B köşesi Şəkil 2'deki gibi C köşesiyle çakışıyor.
6√2
Bu şekilde |DE| = 3√3 br, |DA| = 3 br ve |AC| = 6√2 br
olduğuna göre, Şekil 1'de (AG) uzunluğu kaç birim-
dir?
A) 2√3
C) 3√2 D) 2√5 E) 2√6](https://media.kunduz.com/media/question/seo/raw/20230321172630885758-4581982.jpeg?w=256)
Geometri
Üçgende İç ve Dış AçıortayB
E
G
B) 4
3√3
CE
Şekil 1
Şekil 2
Şekil 1'deki ABC dik üçgeni biçimli kâğıtta BA I AC ve G
ağırlık merkezidir. Bu kâğıt [DE] boyunca katlandığında
B köşesi Şəkil 2'deki gibi C köşesiyle çakışıyor.
6√2
Bu şekilde |DE| = 3√3 br, |DA| = 3 br ve |AC| = 6√2 br
olduğuna göre, Şekil 1'de (AG) uzunluğu kaç birim-
dir?
A) 2√3
C) 3√2 D) 2√5 E) 2√6
![33. D
A
A)
3|2
B)
B
1. Şekil
II. Şekil
ABCD dik yamuğunun taralı BCD bölgesi I. Şekil'deki gibi
[DB] boyunca katlanıyor. C noktası [AD] üzerinde C' nokta-
sına geliyor.
Buna göre, I. Şekil'deki
43
C'
AB
|DC|
x
A
oranı kaçtır?
C) 2
D)
5/2
E) 3](https://media.kunduz.com/media/question/seo/raw/20230322064141114076-4966418.jpg?w=256)
Geometri
Üçgende İç ve Dış Açıortay33. D
A
A)
3|2
B)
B
1. Şekil
II. Şekil
ABCD dik yamuğunun taralı BCD bölgesi I. Şekil'deki gibi
[DB] boyunca katlanıyor. C noktası [AD] üzerinde C' nokta-
sına geliyor.
Buna göre, I. Şekil'deki
43
C'
AB
|DC|
x
A
oranı kaçtır?
C) 2
D)
5/2
E) 3
![36. Ön yüzü mavi, arka yüzü kırmızı olan ABC üçgeni şek-
lindeki kâğıt Şekil 1'de verilmiştir.
*
B
Şekil 1
Bu kâğıt, A köşesi A' noktası ile çakışacak şekilde [BD]
boyunca katlanıyor.
12
A) 4√2
R2
B
+bxŞekil
B) 6√2
A'
X
8
2d
|AD| = 2 cm, |CD| = 8 cm ve m(DBC) = 2m(ABD)'dir.
Buna göre, |BC| = x kaç cm'dir?
C) 8√2
2410
22
2 bin tad malias
D) 7√√3
8√3
Diğer sayfaya geçiniz.](https://media.kunduz.com/media/question/seo/raw/20230322043220598580-5113095.jpeg?w=256)
Geometri
Üçgende İç ve Dış Açıortay36. Ön yüzü mavi, arka yüzü kırmızı olan ABC üçgeni şek-
lindeki kâğıt Şekil 1'de verilmiştir.
*
B
Şekil 1
Bu kâğıt, A köşesi A' noktası ile çakışacak şekilde [BD]
boyunca katlanıyor.
12
A) 4√2
R2
B
+bxŞekil
B) 6√2
A'
X
8
2d
|AD| = 2 cm, |CD| = 8 cm ve m(DBC) = 2m(ABD)'dir.
Buna göre, |BC| = x kaç cm'dir?
C) 8√2
2410
22
2 bin tad malias
D) 7√√3
8√3
Diğer sayfaya geçiniz.
