Üçgenlerde Benzerlik Soruları
![2.
B
A
C
Yukarıdaki şekilde O ve M merkezli çemberlerin yarıçap-
ları 1 cm ve 4 cm'dir. Bu iki çember ABC üçgenine içten
birbirlerine ise dıştan teğettir.
A)
32
3
M
Buna göre, ABC üçgeninin [BC] kenarına ait yüksekliği
kaç cm'dir?
B)
41
4
1
ABC üçgen
|AB| = |ACI
C)
21
2
D)
34
3
E)
35
3](https://media.kunduz.com/media/question/seo/raw/20230220191633885208-1414924.jpg?w=256)
Geometri
Üçgenlerde Benzerlik2.
B
A
C
Yukarıdaki şekilde O ve M merkezli çemberlerin yarıçap-
ları 1 cm ve 4 cm'dir. Bu iki çember ABC üçgenine içten
birbirlerine ise dıştan teğettir.
A)
32
3
M
Buna göre, ABC üçgeninin [BC] kenarına ait yüksekliği
kaç cm'dir?
B)
41
4
1
ABC üçgen
|AB| = |ACI
C)
21
2
D)
34
3
E)
35
3

Geometri
Üçgenlerde Benzerlik38. Bir üçgenin içinde seçilen bir noktadan üçgenin kenarla-
rina paralel olacak biçimde şekildeki gibi doğrular çizili-
yor. Bu durumda oluşan üçgenler sarı, kırmızı ve maviye
boyanıyor. Dörtgenler ise yeşil, mor ve turuncu renge
boyanıyor.
Sarı, kırmızı ve mavi bölgelerin alanları sırasıyla 1 san-
timetrekare, 16 santimetrekare ve 9 santimetrekaredir.
Buna göre, mor bölgenin alanı, turuncu ve yeşil böl-
gelerin alanlarının toplamından kaç santimetrekare
fazladır?
A) 10
B) 12
C) 13
D) 14
E) 15

Geometri
Üçgenlerde Benzerlik9.
olduğuna göre AD = x kaç santimetredir?
göre JADI
B) 2,5
C) 3 D) 4
A) 2
L
S
A) 5 (B) 6
D
ABC üçgeninde, m(ABC) = m(ACD) = m(DCB)
|BC| = 5 br, |AC| = 4 br
olduğuna göre |AB| kaç birimdir?
... tonguç kampüs ...
5
E) 5
1
C) 7 D) 7,5 E) 8

Geometri
Üçgenlerde Benzerlik7.
-5
A) 2
6
AY
B) 3
O
-2
B(3,0)
Analitik düzlemde A, B ve C noktaları veriliyor.
Enes, B noktasını, x ekseni üzerinde sağa ya da sola
kaydırarak |AB| + |BC| toplamının en küçük değerini
bulmak istemektedir.
Buna göre, Enes, B noktasının yerini kaç birim de-
ğiştirmelidir?
A
C) 4
7
D) 5
10.
E) 6
OA
[BA
Dil
d₁
na
A

Geometri
Üçgenlerde Benzerlik34.
M
B
K L
C.
N
IBCI= 10 cm, IKLI = 4 cm, IABI // IMNI
Rizaberk satranç turnuvasında kazandığı 70 cm uzun-
luğunda bir ip ile bağlı madalyasını ve kare dik prizma
üzerine monte edilmiş olan kupasını çalışma masası-
nın üzerine ip kare dik prizmanın tabanındaki üç yüze-
yine değecek biçimde şekildeki gibi koymuştur.
Buna göre, madalyanın masa yüzeyinden aşağıya
sarkan ipinin toplam uzunuğu kaç cm'dir?
A) 12
B) 14 C) 16 D) 18
E) 20
Geometri
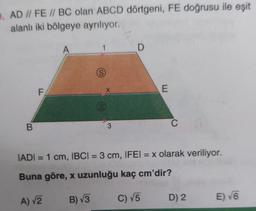
Üçgenlerde Benzerlik9. AD // FE // BC olan ABCD dörtgeni, FE doğrusu ile eşit
alanlı iki bölgeye ayrılıyor.
B
F
A
S
B) √3
X
3
D
E
C
IADI= 1 cm, IBCI= 3 cm, IFEI = x olarak veriliyor.
Buna göre, x uzunluğu kaç cm'dir?
A) √2
C) √5
D) 2
E) √6
Geometri
Üçgenlerde Benzerliküzere, Şekill'de ve-
tonda ABED dörtgeni
renge boyandıktan
parçaya ayrılıyor.
B
A
*****
B
8
3k-z
C
boyalı dörtgenin
si kaç birimdir?
3
E) 28
=9
DK
B
$
A
A
M
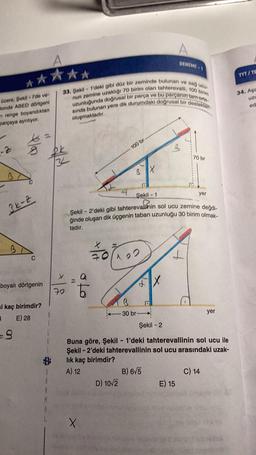
33. Şekil 1'deki gibi düz bir zeminde bulunan ve sağ ucu-
nun zemine uzaklığı 70 birim olan tahterevalli, 100 birim
uzunluğunda doğrusal bir parça ve bu parçanın tam orta-
sında bulunan yere dik durumdaki doğrusal bir destekton
oluşmaktadır.
70
oto
70
X
100 br
BX
D
Şekil -1
yer
Şekil - 2'deki gibi tahterevallinin sol ucu zemine değdi-
ğinde oluşan dik üçgenin taban uzunluğu 30 birim olmak-
tadır.
D) 10/2
22
B
30 br
X
B) 6√5
A
P
DENEME-1
L
Şekil - 2
Buna göre, Şekil 1'deki tahterevallinin sol ucu ile
Şekil -2'deki tahterevallinin sol ucu arasındaki uzak-
lık kaç birimdir?
A) 12
E) 15
70 br
yer
C) 14
WHA
TYT/TE
34. Aga
UZL
ed
![34.
B
D
A
B
D
E
Şekil 1
B) 12
X
E'
E
C
D'
B'
A'
C
E'
C'
Şekil 2
ABC üçgeni biçimindeki bir kâğıt üzerine [DE} // [BC] ola-
cak şekilde [DE] çizilip Şekil 1 deki gibi boyanıyor.
ABC üçgeni belli bir oranda küçültülerek Şekil 1 deki
A'B'C' üçgeni elde ediliyor.
İki üçgen Şekil 2 deki gibi üst üste yapıştırıldığında
[DE] ile [B'C'] ve A ile A' köşeleri çakışıyor.
Şekil 2 de |DE| = 3. | D'E'| olduğuna göre, Şekil 1 deki
sarı bölgelerin alanları oranı kaç olabilir?
A) 13
C) 10
D) 9
E) 8](https://media.kunduz.com/media/question/seo/raw/20230221070424907837-5041844.jpeg?w=256)
Geometri
Üçgenlerde Benzerlik34.
B
D
A
B
D
E
Şekil 1
B) 12
X
E'
E
C
D'
B'
A'
C
E'
C'
Şekil 2
ABC üçgeni biçimindeki bir kâğıt üzerine [DE} // [BC] ola-
cak şekilde [DE] çizilip Şekil 1 deki gibi boyanıyor.
ABC üçgeni belli bir oranda küçültülerek Şekil 1 deki
A'B'C' üçgeni elde ediliyor.
İki üçgen Şekil 2 deki gibi üst üste yapıştırıldığında
[DE] ile [B'C'] ve A ile A' köşeleri çakışıyor.
Şekil 2 de |DE| = 3. | D'E'| olduğuna göre, Şekil 1 deki
sarı bölgelerin alanları oranı kaç olabilir?
A) 13
C) 10
D) 9
E) 8
![6. Ön yüzü turuncu, arka yüzü mavi olan ABC üçgeni
şeklinde kesilmiş kâğıt parçası verilmiştir.
BE
A
●
D
C
Şekil-1
A) 36
Şekil-2
B
Bu kâğıt;
[AB] kenarı [AC] kenarının üzerine gelecek biçimde
AE boyunca katlandığında şekil-1,
G
B) 39
[AB] kenarı [BC] kenarı üzerine gelecek biçimde BD
boyunca katlandığında şekil-2 elde ediliyor.
D
K
B4 HE
Şekil-3
Şekil-3'te katlama izlerinin kesişimi olan K noktasın-
dan [AB] kenarına paralel [HG] çiziliyor.
• IBHI = 4 cm, IAGI = 5 cm ve IHCI = 12 cm olarak ölçü-
lüyor.
Buna göre, ABC üçgeninin çevresi kaç cm'dir?
C) 40
D) 45
E) 48](https://media.kunduz.com/media/question/seo/raw/20230221063828218085-5230895.jpg?w=256)
Geometri
Üçgenlerde Benzerlik6. Ön yüzü turuncu, arka yüzü mavi olan ABC üçgeni
şeklinde kesilmiş kâğıt parçası verilmiştir.
BE
A
●
D
C
Şekil-1
A) 36
Şekil-2
B
Bu kâğıt;
[AB] kenarı [AC] kenarının üzerine gelecek biçimde
AE boyunca katlandığında şekil-1,
G
B) 39
[AB] kenarı [BC] kenarı üzerine gelecek biçimde BD
boyunca katlandığında şekil-2 elde ediliyor.
D
K
B4 HE
Şekil-3
Şekil-3'te katlama izlerinin kesişimi olan K noktasın-
dan [AB] kenarına paralel [HG] çiziliyor.
• IBHI = 4 cm, IAGI = 5 cm ve IHCI = 12 cm olarak ölçü-
lüyor.
Buna göre, ABC üçgeninin çevresi kaç cm'dir?
C) 40
D) 45
E) 48
![12.
(003
B
BE
E
D
E
Yukarıdaki şekilde; ABC bir üçgen, [DA] [AC],
[BD] [DA], |BA| = |EC| ve A(ABE) = 18 cm² dir.
ubm(BAD) = m(ACE) olduğuna göre, |BD| kaç
cm dir?
A
A) 3√3 (B) 2√7 (C)
√30
C) √√30 D) 4√2 E) 6](https://media.kunduz.com/media/question/seo/raw/20230221054522443878-316077.jpeg?w=256)
Geometri
Üçgenlerde Benzerlik12.
(003
B
BE
E
D
E
Yukarıdaki şekilde; ABC bir üçgen, [DA] [AC],
[BD] [DA], |BA| = |EC| ve A(ABE) = 18 cm² dir.
ubm(BAD) = m(ACE) olduğuna göre, |BD| kaç
cm dir?
A
A) 3√3 (B) 2√7 (C)
√30
C) √√30 D) 4√2 E) 6
![8.
a 19
Y=14 X=6
a (c
5
12 Mishad A
B
|OA| = |
A) 5
15
A
B) 6
E
D
0102/19 sy biebheduy
F
C) 7
5
Şekilde, ABC ve DEC birer üçgen, [AB] // [DE],
m(EDC) = m(ACB), |AB| = 5 cm, |EC| = 5 cm
ve |DC| = 6 cm dir.
Buna göre, |AC| kaç cm dir?
6
C
104
(SAD) 8
E) 9](https://media.kunduz.com/media/question/seo/raw/20230221054425783725-316077.jpeg?w=256)
Geometri
Üçgenlerde Benzerlik8.
a 19
Y=14 X=6
a (c
5
12 Mishad A
B
|OA| = |
A) 5
15
A
B) 6
E
D
0102/19 sy biebheduy
F
C) 7
5
Şekilde, ABC ve DEC birer üçgen, [AB] // [DE],
m(EDC) = m(ACB), |AB| = 5 cm, |EC| = 5 cm
ve |DC| = 6 cm dir.
Buna göre, |AC| kaç cm dir?
6
C
104
(SAD) 8
E) 9
![*****
12. Şekil-l'deki ABCD dikdörtgeni biçimindeki kâğıt [AE] bo-
yunca katlandığında B noktası Şekil-ll'deki gibi B' nokta-
si ile çakışmaktadır.
D
A
3
C
3
E
5
B
Şekil-I
Buna göre, Şekil-ll'deki
A) 25 B) 30
D
A
B
C) 35
3E
Şekil-Il
A(AB'E) kaç cm² dir?
D) 40 E) 45](https://media.kunduz.com/media/question/seo/raw/20230221053853668934-3573788.jpg?w=256)
Geometri
Üçgenlerde Benzerlik*****
12. Şekil-l'deki ABCD dikdörtgeni biçimindeki kâğıt [AE] bo-
yunca katlandığında B noktası Şekil-ll'deki gibi B' nokta-
si ile çakışmaktadır.
D
A
3
C
3
E
5
B
Şekil-I
Buna göre, Şekil-ll'deki
A) 25 B) 30
D
A
B
C) 35
3E
Şekil-Il
A(AB'E) kaç cm² dir?
D) 40 E) 45
![5.
Duvar
90 cm
Ali
480
Mustafa
180
A) 180 B) 160
540 cm
8
Sokak lambasına eşit uzaklıkta bulunan Ali ve Mustafa'nın
-BX boyları eşit ve 180 cm'dir. Mustafa'nın gölge boyu 540 cm
nipive Ali'nin duvara olan uzaklığı 90 cm'dir. [CA]
Buna göre, Ali'nin duvar üstüne düşen gölge boyu kaç
cm'dir? (Sokak lambasının boyu 720 cm dir.)
nsbriest ce
DBC) 150
D) 120 E) 90](https://media.kunduz.com/media/question/seo/raw/20230220164749995813-2258679.jpeg?w=256)
Geometri
Üçgenlerde Benzerlik5.
Duvar
90 cm
Ali
480
Mustafa
180
A) 180 B) 160
540 cm
8
Sokak lambasına eşit uzaklıkta bulunan Ali ve Mustafa'nın
-BX boyları eşit ve 180 cm'dir. Mustafa'nın gölge boyu 540 cm
nipive Ali'nin duvara olan uzaklığı 90 cm'dir. [CA]
Buna göre, Ali'nin duvar üstüne düşen gölge boyu kaç
cm'dir? (Sokak lambasının boyu 720 cm dir.)
nsbriest ce
DBC) 150
D) 120 E) 90
![4.
f
A
E
[AE] // [BF] // [GC]
|CD|= 90 cm,
|CF|= 20 cm,
A) 260
B
Şekilde A, B, C, D doğrusaldır. Top oynayan çocuklardan
birinin topunun izlediği yol gösterilmiştir.
|AB| = 180 cm
|BE| = 60 cm
B) 270
C
olduğuna göre, topun yatayda aldığı yol, |AD| kaç
cm'dir?
C) 330
G
D
D) 390
E) 450](https://media.kunduz.com/media/question/seo/raw/20230220164413689358-2258679.jpeg?w=256)
Geometri
Üçgenlerde Benzerlik4.
f
A
E
[AE] // [BF] // [GC]
|CD|= 90 cm,
|CF|= 20 cm,
A) 260
B
Şekilde A, B, C, D doğrusaldır. Top oynayan çocuklardan
birinin topunun izlediği yol gösterilmiştir.
|AB| = 180 cm
|BE| = 60 cm
B) 270
C
olduğuna göre, topun yatayda aldığı yol, |AD| kaç
cm'dir?
C) 330
G
D
D) 390
E) 450
Geometri
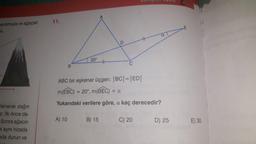
Üçgenlerde Benzerlikardımıyla ve ağaçlar
u.
"lanarak dağın
z: İlk önce da-
Sonra ağacın
i aynı hizada
ada durun ve
11.
B
A) 10
20° #
B) 15
D
ABC bir eşkenar üçgen. |BC| = |ED|
m(EBC)
= 20°, m(BEC) =
Yukarıdaki verilere göre, a kaç derecedir?
=a
C
Denom 10ULI
C) 20
D) 25
E) 30

Geometri
Üçgenlerde BenzerlikBL
lar
tik
10.
D
A) 4
B
B) 5
E
2
ABC bir üçgen. m(CDF) = m(BAC)
|EB| = 2 cm, |DE| = |EF|= 4 cm, |AF|= 6 cm
Yukarıdaki verilere göre, |BC| = x kaç cm'dir?
4
C) 6
D) 7
E) 8
12.
ABC ve FBC
|EF|-|ED
|BC| = 14
Yukarıdaki
A) 3
