Pisagor Teoremi Soruları
Geometri
Pisagor Teoremi7.
A)
E
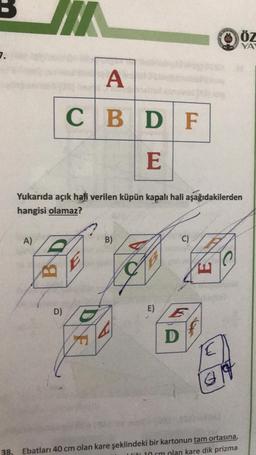
Yukarıda açık hali verilen küpün kapalı hali aşağıdakilerden
hangisi olamaz?
B
A
CBD F
D)
E
B)
E)
D
C)
E
G
ÖZ
YA
38. Ebatları 40 cm olan kare şeklindeki bir kartonun tam ortasına,
Wiži 10 cm plan kare dik prizma
Geometri
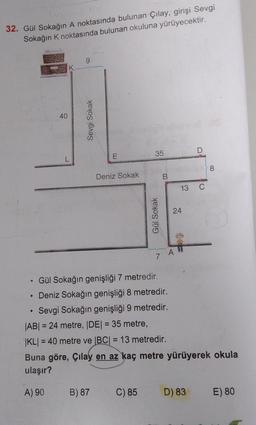
Pisagor Teoremi32. Gül Sokağın A noktasında bulunan Çılay, girişi Sevgi
Sokağın K noktasında bulunan okuluna yürüyecektir.
A
●
40
L
9
Sevgi Sokak
E
Deniz Sokak
B) 87
35
Gül Sokak
C) 85
B
Gül Sokağın genişliği 7 metredir.
Deniz Sokağın genişliği 8 metredir.
Sevgi Sokağın genişliği 9 metredir.
A
24
13 C
D
|AB| = 24 metre, |DE| = 35 metre,
|KL| = 40 metre ve |BC| = 13 metredir.
Buna göre, Çilay en az kaç metre yürüyerek okula
ulaşır?
A) 90
D) 83
8
E) 80
Geometri
Pisagor Teoremiunca
ktası
ala-
öre,
Testokul
55
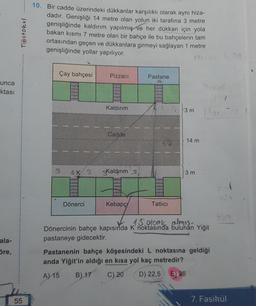
10. Bir cadde üzerindeki dükkanlar karşılıklı olarak aynı hiza-
dadır. Genişliği 14 metre olan yolun iki tarafına 3 metre
genişliğinde kaldırım yapılmış ve her dükkan için yola
bakan kısmı 7 metre olan bir bahçe ile bu bahçelerin tam
ortasından geçen ve dükkanlara girmeyi sağlayan 1 metre
genişliğinde yollar yapılıyor.
Çay bahçesi
3
4K 3
Dönerci
Pizzacı
Kaldırım
Cadde
Kaldırım s
Kebapç
Pastane
Tatlıcı
3 m
14 m
3 m
lox
15. glook almis-
Dönercinin bahçe kapısında K' noktasında bulunan Yiğit
pastaneye gidecektir.
Pastanenin bahçe köşesindeki L noktasına geldiği
anda Yiğit'in aldığı en kısa yol kaç metredir?
A) 15 B) 17
C) 20 D) 22,5 E) 25
369
7. Fasikül
20.
Geometri
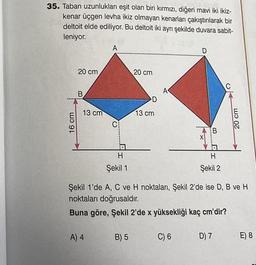
Pisagor Teoremi35. Taban uzunlukları eşit olan biri kırmızı, diğeri mavi iki ikiz-
kenar üçgen levha ikiz olmayan kenarları çakıştırılarak bir
deltoit elde ediliyor. Bu deltoit iki aynı şekilde duvara sabit-
leniyor.
16 cm
20 cm,
B
13 cm
A
C
a
H
Şekil 1
20 cm
B) 5
D
13 cm
D
C) 6
******
AB
H
Şekil 2
Şekil 1'de A, C ve H noktaları, Şekil 2'de ise D, B ve H
noktaları doğrusaldır.
Buna göre, Şekil 2'de x yüksekliği kaç cm'dir?
A) 4
C
D) 7
20 cm
E) 8

Geometri
Pisagor Teoremi33.
Ahmet
ABC dik üçgeni biçimindeki bir adacığın B köşesinden Ah-
met ve Mehmet üçgenin sırasıyla A ve C köşelerini geçe-
rek, B köşesine ait açıortayın AC kenarını kestiği noktada
buluşacaktır.
Mehmet
|AB| = 21 m ve |BC| = 28 m olduğuna göre,
Mehmet'in yürümesi gereken yolun uzunluğu Ahmet'in
yürümesi gereken yolun uzunluğundan kaç m fazla-
dır?
A) 5
B) 7
C) 12
D) 13
E) 17
Geometri
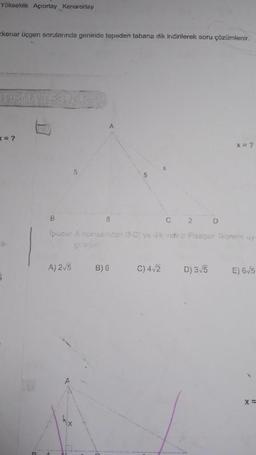
Pisagor TeoremiYükseklik Açıortay Kenarortay
kenar üçgen sorularında genelde tepeden tabana dik indirilerek soru çözümlenir.
<= ?
a-
B
5
A) 2√5
C 2
(pucu: A noitesindan (5C) ve Jk indirip Pisagor Teoremi uy-
A
8
B) 6
C) 4√2
D) 3√5
X=?
D
E) 6√5
X=
![= = 14
ABC dik üçgen
[AB] [AC]
|AB| = 8 cm
|BD| = 12 cm
|CD| = 4 cm
O 4 C
DI = x kaç cm'dir?
D4√6(E) 4√7
ORIJINAL YAYINLARI
4.12 = 4812
Y
11.
e
36 = 28K²
36
=K²
C
DO
2√5
EX
2+2
8
23/15
B
ABC dik üçgen
[AB]1[BC]
[ED]L[AC]
|AD|=|DC|
ICE>|EB|
|AB| = 8 cm
|DE| = 2√5 cm
Yukarıdaki verilere göre, |EB| = x kaç cm'dir?
A) 4
B) 5
C) 6
D) 4√3
E) 8
A) 3
B
3,
Yukarıdaki ve
tır?
A)
A
5 B)](https://media.kunduz.com/media/question/seo/raw/20230110175705527914-4384340.jpg?w=256)
Geometri
Pisagor Teoremi= = 14
ABC dik üçgen
[AB] [AC]
|AB| = 8 cm
|BD| = 12 cm
|CD| = 4 cm
O 4 C
DI = x kaç cm'dir?
D4√6(E) 4√7
ORIJINAL YAYINLARI
4.12 = 4812
Y
11.
e
36 = 28K²
36
=K²
C
DO
2√5
EX
2+2
8
23/15
B
ABC dik üçgen
[AB]1[BC]
[ED]L[AC]
|AD|=|DC|
ICE>|EB|
|AB| = 8 cm
|DE| = 2√5 cm
Yukarıdaki verilere göre, |EB| = x kaç cm'dir?
A) 4
B) 5
C) 6
D) 4√3
E) 8
A) 3
B
3,
Yukarıdaki ve
tır?
A)
A
5 B)
![A) 2√15
B) 3√7
T
C) 8
B D
D) 6√2
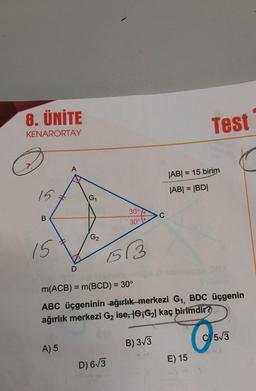
35. Aşağıda verilen ABC ikizkenar üçgenin içine şekildeki gibi
DCET dikdörtgeni yerleştirildiğinde dikdörtgenin [TE] kenarı
ABC üçgeninin ağırlık merkezinden geçmiştir.
A
KE
E) 2√19
C
TOP 37. ABC VE
[BC] ve
|AB| = |AC| = 15 cm, |BC| = 18 cm
olduğuna göre, DCET dikdörtgeninin alanı kaç cm² dir?
A) 54
B) 60
C) 64
D) 72
E) 76
AB
m(A
Şek
olu
A)](https://media.kunduz.com/media/question/seo/raw/20230110090546256985-4954981.jpg?w=256)
Geometri
Pisagor TeoremiA) 2√15
B) 3√7
T
C) 8
B D
D) 6√2
35. Aşağıda verilen ABC ikizkenar üçgenin içine şekildeki gibi
DCET dikdörtgeni yerleştirildiğinde dikdörtgenin [TE] kenarı
ABC üçgeninin ağırlık merkezinden geçmiştir.
A
KE
E) 2√19
C
TOP 37. ABC VE
[BC] ve
|AB| = |AC| = 15 cm, |BC| = 18 cm
olduğuna göre, DCET dikdörtgeninin alanı kaç cm² dir?
A) 54
B) 60
C) 64
D) 72
E) 76
AB
m(A
Şek
olu
A)

Geometri
Pisagor Teoremi30°
D
B
B
|AB| =
Özel Üçgenler
E) 6√3
alem ile
7. Murat, hipotenüs uzunlukları eşit olan dik üçgen biçimindeki il
kartonu şekildeki gibi dik açılarını birleştirerek kenarlarını çakıştı.
lin kenarlarının arasındaki uzunlukları ölçtüğünde AD = 3 cm,
rip yeni bir şekil elde etmiştir. Murat, daha sonra elde ettiği şek
|BD| = 6 cm ve |AC| = 7 cm olduğunu görmüştür.
6
D
3
A
7
B
Buna göre, |EC| = x kaç cm'dir?
A) 2
B) 2√2
C) 3
C
X
D) 2√3
E
1.
E) 4
Yükse
merd
1,5 m
![şekilde
zaklığı
3. Aşağıdaki şekilde ABC dik üçgeni biçimindeki bir kâğıt, AD
boyunca katlandığında C noktası [AB] üzerindeki C' noktasına
gelmektedir.
B 5
4
A) 28
C B
C
C) 32
D
5 D
Şekil 1
Şekil 2
ABC bir dik üçgen, AC 1 BC, |DC| = 4 cm, |BD| = 5 cm
Buna göre, Çevre(ABC) kaç cm'dir?
B) 30
DEĞERLENDİRME TES
D) 34
C
E) 36](https://media.kunduz.com/media/question/seo/raw/20230109194633822956-636395.jpeg?w=256)
Geometri
Pisagor Teoremişekilde
zaklığı
3. Aşağıdaki şekilde ABC dik üçgeni biçimindeki bir kâğıt, AD
boyunca katlandığında C noktası [AB] üzerindeki C' noktasına
gelmektedir.
B 5
4
A) 28
C B
C
C) 32
D
5 D
Şekil 1
Şekil 2
ABC bir dik üçgen, AC 1 BC, |DC| = 4 cm, |BD| = 5 cm
Buna göre, Çevre(ABC) kaç cm'dir?
B) 30
DEĞERLENDİRME TES
D) 34
C
E) 36

Geometri
Pisagor Teoremi33. Serkan, ABC dik üçgeni biçimindeki kâğıdı Şekil 1'deki
gibi B ve C köşelerinden DE ve KL doğruları boyunca
katladığında Şekil 2'deki görünümü elde ediyor.
A
D
B E
A) 6√3
WUJ
A
K
LC. B
D
DT4√3
DX14√3
Şekil 1
Şekil 2
Şekil 2'de |DE| = 8 birim ve |KL| = 6 birim olduğuna
göre, Şekil 1'de BC uzunluğu kaç birimdir?
Ja
E
B) 9√3
VE) 15√3
sus
K
C) 12√3
403
C
3
![Orkun, Şekil 1'de verilen [AB] çaplı O merkezli daire şek-
lindeki bir kartonu [EF] ve [KL] üzerinden Şekil 2'deki gibi
kathiyor.
B
A
Şekil 1
E
B
$0
A
Şekil 2
D) 20
N
[EF] // [AB] // [KL]
|AB| = 50 cm, |EF| = 40 cm, IKLI = 30 cm
[BM] ve [BN] sırasıyla EF ve KL yayına teğet olduğuna
göre, |BN|- |BM| farkı kaç cm'dir?
A) 5
B) 10
C) 15
E) 25](https://media.kunduz.com/media/question/seo/raw/20230107145121377302-3421552.jpg?w=256)
Geometri
Pisagor TeoremiOrkun, Şekil 1'de verilen [AB] çaplı O merkezli daire şek-
lindeki bir kartonu [EF] ve [KL] üzerinden Şekil 2'deki gibi
kathiyor.
B
A
Şekil 1
E
B
$0
A
Şekil 2
D) 20
N
[EF] // [AB] // [KL]
|AB| = 50 cm, |EF| = 40 cm, IKLI = 30 cm
[BM] ve [BN] sırasıyla EF ve KL yayına teğet olduğuna
göre, |BN|- |BM| farkı kaç cm'dir?
A) 5
B) 10
C) 15
E) 25
![8100
3304
W
6.
4a=8
a=2
B
90² +48 = x²
liu
8
30
X
4
4√3
3a
29
ACB dik üçgen, [AC]L[CB], 6|BD| = 2|AD| = 3|AC|
|BC| = 4√3 cm, |DC| = x cm
D) 6
Yukarıdaki verilere göre, |DC| = x kaç cm'dir?
AV 2√7
B) √30
E) 2√10
C) 4√2
C](https://media.kunduz.com/media/question/seo/raw/20230105165817202084-2433745.jpeg?w=256)
Geometri
Pisagor Teoremi8100
3304
W
6.
4a=8
a=2
B
90² +48 = x²
liu
8
30
X
4
4√3
3a
29
ACB dik üçgen, [AC]L[CB], 6|BD| = 2|AD| = 3|AC|
|BC| = 4√3 cm, |DC| = x cm
D) 6
Yukarıdaki verilere göre, |DC| = x kaç cm'dir?
AV 2√7
B) √30
E) 2√10
C) 4√2
C
Geometri
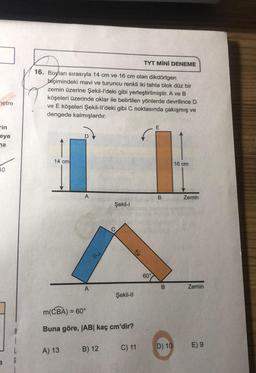
Pisagor Teoremi8. ÜNİTE
KENARORTAY
15
B
15
A
A) 5
D
G₁
G2
30°
30°
1513
D) 6√3
C
m(ACB) = m(BCD) = 30°
ABC üçgeninin ağırlık merkezi G₁, BDC üçgenin
ağırlık merkezi G₂ ise, 1G1G₂| kaç birimdir?
B) 3√3
Test
|AB| = 15 birim
|AB| = |BD|
E) 15
O
C)5√3
Geometri
Pisagor Teoreminetre
rin
eye
na
10
3
TYT MİNİ DENEME
16. Boyları sırasıyla 14 cm ve 16 cm olan dikdörtgen
biçimindeki mavi ve turuncu renkli iki tahta blok düz bir
zemin üzerine Şekil-l'deki gibi yerleştirilmiştir. A ve B
köşeleri üzerinde oklar ile belirtilen yönlerde devrilince D
ve E köşeleri Şekil-ll'deki gibi C noktasında çakışmış ve
dengede kalmışlardır.
14 cm
A
A) 13
A
Şekil-l
m(CBA) = 60°
Buna göre, |AB| kaç cm'dir?
B) 12
Şekil-II
C) 11
16
60°
E
B
B
D) 10
16 cm
Zemin
Zemin
E) 9
![kağıt [KL]
kenan
B
32. Nehir üzerine yapılan köprünün bir kısmı şekildeki gibi
çizilmiştir. Köprüyü desteklemek için TB ve TC halatlari
şekildeki gibi zemine sabitleniyor.
Buna göre, ITC kaç metredir?
A) 75√2
B) 80/2
D) 80√5
[AT]L[AC], IABI= 30 metre, |BC| = 50 metre ve B nok-
tasının A noktasına uzaklığı, [TC] halatına uzaklığına
eşittir.
60
30
30
30 30
E) 100
60
50
30
40
C) 80√3](https://media.kunduz.com/media/question/seo/raw/20221231185728907842-4800518.jpeg?w=256)
Geometri
Pisagor Teoremikağıt [KL]
kenan
B
32. Nehir üzerine yapılan köprünün bir kısmı şekildeki gibi
çizilmiştir. Köprüyü desteklemek için TB ve TC halatlari
şekildeki gibi zemine sabitleniyor.
Buna göre, ITC kaç metredir?
A) 75√2
B) 80/2
D) 80√5
[AT]L[AC], IABI= 30 metre, |BC| = 50 metre ve B nok-
tasının A noktasına uzaklığı, [TC] halatına uzaklığına
eşittir.
60
30
30
30 30
E) 100
60
50
30
40
C) 80√3
