Üçgende Kenarortay Soruları

Geometri
Üçgende Kenarortay6.
Kr
12
u
B
10
A
X
G
u
13
13
2k
ABC bir ikizkenar üçgen, G, ağırlık merkezi
|AC| = |BC| = 13 cm, |AB| = 10 cm, |AG| = x
Yukarıdaki verilere göre, x kaç cm'dir?
A) 3√3 B) 4√2
C
C) 6
<=> x ² = 25+16
x = √ulem
D) 39 E)√41
Geometri
Üçgende Kenarortay✔
B
E
A
C
F
2m
3(k+m1 = 24
8 cm
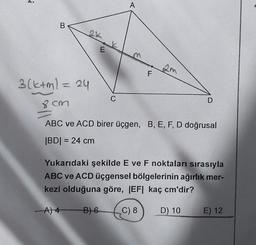
ABC ve ACD birer üçgen, B, E, F, D doğrusal
|BD| = 24 cm
D
Yukarıdaki şekilde E ve F noktaları sırasıyla
ABC ve ACD üçgensel bölgelerinin ağırlık mer-
kezi olduğuna göre, |EF| kaç cm'dir?
A) 4 B) 6
C) 8
D) 10
E) 12
![E
doğru Tolga ile
er de aynı şekil-
sağa doğru yü-
Caner ve Gök-
n tahminine gö-
120
E) 125
4.
B
X
D
F
E
20
C
ABC bir üçgen, [DE] [BC], [AE] açıortay, m(ACB) = 20°,
|DC| = 2|AE|
Yukarıdaki verilere göre, m(ABC) = x kaç derecedir?
A) 80
B) 70
C) 60
D) 50
E) 40
X Large TEST (Tarama)](https://media.kunduz.com/media/question/seo/raw/20230208185201671927-4836116.jpg?w=256)
Geometri
Üçgende KenarortayE
doğru Tolga ile
er de aynı şekil-
sağa doğru yü-
Caner ve Gök-
n tahminine gö-
120
E) 125
4.
B
X
D
F
E
20
C
ABC bir üçgen, [DE] [BC], [AE] açıortay, m(ACB) = 20°,
|DC| = 2|AE|
Yukarıdaki verilere göre, m(ABC) = x kaç derecedir?
A) 80
B) 70
C) 60
D) 50
E) 40
X Large TEST (Tarama)

Geometri
Üçgende Kenarortay6
612=35
XIN
E
1212
D) 3√3
6
402
C
{F}
EC| = 6 cm, |FB| = x
E) 4√2
60
6.
222
3 (3
B
Add to bribagi 08
A (08) [BAY
108
B)
+
E
+
ABC üçgen,
|BF| = |FE| = |ED| ve |AD| = |DC| dir.
|AE| = 6 cm olduğuna göre, |KL| = x kaç cm'dir?
A) 1
C) 2
D)
C
N|G
Dre
E
Kenar: 8
Kenarortay Uzunluğu: x
B
Buna göre, x kaçtır?
A) 4
B) 6
Kenar: 10
Kenarortay Uzunluğu: 5
C) 2√13
D) 3√13
E)√2
![DB'
duğuna
4√3
13. Şekilde verilen ABC üçgeninin [AC] doğru parçasına göre
yansıması AB'C üçgenidir.
B
60°
Deneme
A) 4
|AB| = 4√3 birim
m(BAC) = 60°
B) 4√2
C) 6
D) 8
Buna göre, ABC ile AB'C üçgensel bölgelerinin ağırlık
merkezleri arasındaki uzaklık kaç birimdir?
E) 6√3](https://media.kunduz.com/media/question/seo/raw/20230207181953609511-5153674.jpg?w=256)
Geometri
Üçgende KenarortayDB'
duğuna
4√3
13. Şekilde verilen ABC üçgeninin [AC] doğru parçasına göre
yansıması AB'C üçgenidir.
B
60°
Deneme
A) 4
|AB| = 4√3 birim
m(BAC) = 60°
B) 4√2
C) 6
D) 8
Buna göre, ABC ile AB'C üçgensel bölgelerinin ağırlık
merkezleri arasındaki uzaklık kaç birimdir?
E) 6√3
Geometri
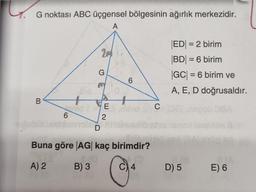
Üçgende KenarortayG noktası ABC üçgensel bölgesinin ağırlık merkezidir.
A
B
6
+
B) 3
20%
G
D
E2
6
Buna göre |AG| kaç birimdir?
8.(0
A) 2
C) 4
C
|ED| = 2 birim
|BD| = 6 birim
|GC| = 6 birim ve
A, E, D doğrusaldır.
D) 5
E) 6
![B'
2
ğuna
len ADB'
A) 4
7
2
4√3
1326
60°
21.
162
CA
G₁
yansıması AB'C üçgenidir.
13. Şekilde verilen AB ingenio [C] doğru parçasına
G
3
20
C) 6
Deneme - 7
merkezleri arasındaki uzaklık kaç birimdir?
Buna göre, ABC ile AB'C üçgensel bölgelerinin ağırlık
B) 4√2
|AB| = 4√3 birim
m(BAC) = 60°
D) 8
göre
E) 6√3
ENKOⓇ
A2](https://media.kunduz.com/media/question/seo/raw/20230207190116544315-5153674.jpg?w=256)
Geometri
Üçgende KenarortayB'
2
ğuna
len ADB'
A) 4
7
2
4√3
1326
60°
21.
162
CA
G₁
yansıması AB'C üçgenidir.
13. Şekilde verilen AB ingenio [C] doğru parçasına
G
3
20
C) 6
Deneme - 7
merkezleri arasındaki uzaklık kaç birimdir?
Buna göre, ABC ile AB'C üçgensel bölgelerinin ağırlık
B) 4√2
|AB| = 4√3 birim
m(BAC) = 60°
D) 8
göre
E) 6√3
ENKOⓇ
A2
![13)
HH
Yukarıda birim karelere bölünmüş zemin üzerin-
de verilen ABC üçgeni için aşağıdakilerden han-
gisi ya da hangileri doğrudur?
B
I. |BC| > |AB| > |AC| dir.
II. m(Â) > 90° dir.
III. [AB] kenarına ait kenarortay uzunluğu 5√2 bi-
rimdir.
A) Yalnız I
D) I ve III
C
B) Yalnız II
E) I, II ve III
C) I ve II](https://media.kunduz.com/media/question/seo/raw/20230207143117974793-5159517.jpg?w=256)
Geometri
Üçgende Kenarortay13)
HH
Yukarıda birim karelere bölünmüş zemin üzerin-
de verilen ABC üçgeni için aşağıdakilerden han-
gisi ya da hangileri doğrudur?
B
I. |BC| > |AB| > |AC| dir.
II. m(Â) > 90° dir.
III. [AB] kenarına ait kenarortay uzunluğu 5√2 bi-
rimdir.
A) Yalnız I
D) I ve III
C
B) Yalnız II
E) I, II ve III
C) I ve II
![B
A
15
8
D) 6√3
G
T
111
E
X
D
Şekilde ABC ve BDC üçgen,
G, ABC üçgeninin ağırlık merkezi,
[DE] açıortay, G E [AE],
|BD| = 15 cm, |AG| = 8 cm
olduğuna göre, |DE| = x kaç cm dir?
A) 4√5
B) 9
C) 3√10
C
E) 12
11.
6
A)
E
6
Şekil
[AD]
|AE|
olduğ](https://media.kunduz.com/media/question/seo/raw/20230207134239383787-698603.jpg?w=256)
Geometri
Üçgende KenarortayB
A
15
8
D) 6√3
G
T
111
E
X
D
Şekilde ABC ve BDC üçgen,
G, ABC üçgeninin ağırlık merkezi,
[DE] açıortay, G E [AE],
|BD| = 15 cm, |AG| = 8 cm
olduğuna göre, |DE| = x kaç cm dir?
A) 4√5
B) 9
C) 3√10
C
E) 12
11.
6
A)
E
6
Şekil
[AD]
|AE|
olduğ
![a
15.
B
LL
F
mat
3
4
8
E
D
3L
lek
Yukarıdaki verilere göre ABC üçgeninin hipotenüsünün
uzunluğu kaç br'dir?
|BC|
A) 5
B) 6
D) 6√2
ABC üçgen
G ağırlık merkezi
[BA] [AC]
|FG| = 3 br
|EG| = 4 br
C) 5√3
E) 6√5](https://media.kunduz.com/media/question/seo/raw/20230207110101881167-2974560.jpg?w=256)
Geometri
Üçgende Kenarortaya
15.
B
LL
F
mat
3
4
8
E
D
3L
lek
Yukarıdaki verilere göre ABC üçgeninin hipotenüsünün
uzunluğu kaç br'dir?
|BC|
A) 5
B) 6
D) 6√2
ABC üçgen
G ağırlık merkezi
[BA] [AC]
|FG| = 3 br
|EG| = 4 br
C) 5√3
E) 6√5

Geometri
Üçgende KenarortayE) 24
48
4.
A
34
16
31 3
B
10
10
C
Şekil I
Futbol sahasının köşe bayraklarından birisi Şekill'de
|AB| = 16 birim, |AC| = |BC| = 10 birim olacak şekilde veri-
liyor. B köşesini tutan çivi çıkınca bayrak kaymış ve
Şekil Il'deki görüntü oluşmuştur.
B) 7
B
G noktası AB'C' üçgeninin ağırlık merkezi ise |AG| kaç
birimdir?
A) 2√17
A
C) 6
Şekil II
D) 4√3
E) 2√3
DIA

Geometri
Üçgende Kenarortay37.
20 birim
Bir kenarının uzunluğu 20 birim olan kare şeklindeki bir
kartonun kenar uzunluğu x birim olan birer kare kesilerek
çıkartılıyor ve kalan karton parçası kıvrılarak şekildeki
gibi üstü açık bir lokum kutusu yapılıyor.
Bu kutunun alanı 336 birim kare olduğuna göre, x kaç
birimdir?
A) 12
B) 10
C) 8 (D) 6
E) 4
22
![4. BIR KENARORTAYIN KENARI ÜZERİNDEKİ DİK
İZDÜŞÜMÜ
B
ÖRNEK
214 H₂X6D
a
6
II
ABC üçgeninde IABI= 13 cm, IACI = 11 cm, IBDI = IDC| = 5 cm
[AB] kenarortayının [BC] kenarı üzerindeki dik izdüşümü-
nün uzunluğu kaç cm dir?
ABC herhangi bir üçgen, a, b, c kenar uzunlukları iken V
kenar ortayının [BC] kenarı üzerindeki dik izdüşümünün
uzunluğu
IHDI = x dir.
b> ciken IHDI = x=
ÇÖZÜM
b²-c²
2a
dir.](https://media.kunduz.com/media/question/seo/raw/20230205115049742175-5340232.jpg?w=256)
Geometri
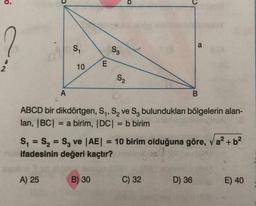
Üçgende Kenarortay4. BIR KENARORTAYIN KENARI ÜZERİNDEKİ DİK
İZDÜŞÜMÜ
B
ÖRNEK
214 H₂X6D
a
6
II
ABC üçgeninde IABI= 13 cm, IACI = 11 cm, IBDI = IDC| = 5 cm
[AB] kenarortayının [BC] kenarı üzerindeki dik izdüşümü-
nün uzunluğu kaç cm dir?
ABC herhangi bir üçgen, a, b, c kenar uzunlukları iken V
kenar ortayının [BC] kenarı üzerindeki dik izdüşümünün
uzunluğu
IHDI = x dir.
b> ciken IHDI = x=
ÇÖZÜM
b²-c²
2a
dir.
Geometri
Üçgende KenarortayA
S₁
A) 25
10
E
S3
B) 30
S₂
ABCD bir dikdörtgen, S₁, S₂ ve S₂ bulundukları bölgelerin alan-
ları, |BC| = a birim, |DC| = b birim
=
S₁ S₂ S3 ve |AE| = 10 birim olduğuna göre, a² + b²
ifadesinin değeri kaçtır?
(=?
a
B
C) 32
D) 36
E) 40
![5.
75⁰
30°
75°
B 60°
E
15%
D
15°
60°
30°
C
Şekil -1
Şekil - II
ARMAD
Şekilerde görülen eş [BC] tabanı ile (15- 75 - 90) ve
(30-60-90) derecelik açılara sahip üçgenlerin dik açı-
larının bulunduğu köşeleri birleştiren doğru parçaları-
nın uzunlukları oranı kaç olabilir?
A) √3
B) 1
√3-1
C)/3-1 D) 2√2 E) √3+1
UIACA](https://media.kunduz.com/media/question/seo/raw/20230202190641196240-3024463.jpg?w=256)
Geometri
Üçgende Kenarortay5.
75⁰
30°
75°
B 60°
E
15%
D
15°
60°
30°
C
Şekil -1
Şekil - II
ARMAD
Şekilerde görülen eş [BC] tabanı ile (15- 75 - 90) ve
(30-60-90) derecelik açılara sahip üçgenlerin dik açı-
larının bulunduğu köşeleri birleştiren doğru parçaları-
nın uzunlukları oranı kaç olabilir?
A) √3
B) 1
√3-1
C)/3-1 D) 2√2 E) √3+1
UIACA
Geometri
Üçgende Kenarortay7.
A
D
D
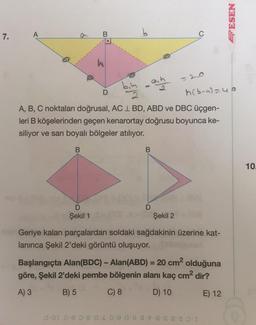
Şekil 1
bin
Com
2
b
0-01 0-6 0-8 A-4
aih
B
h(b-a)=40
A, B, C noktaları doğrusal, AC L BD, ABD ve DBC üçgen-
leri B köşelerinden geçen kenarortay doğrusu boyunca ke-
siliyor ve sarı boyalı bölgeler atılıyor.
-
D
C
Şekil 2
Geriye kalan parçalardan soldaki sağdakinin üzerine kat-
lanınca Şekil 2'deki görüntü oluşuyor.
Başlangıçta Alan(BDC) - Alan(ABD) = 20 cm² olduğuna
göre, Şekil 2'deki pembe bölgenin alanı kaç cm² dir?
A) 3
B) 5
C) 8
D) 10
E) 12
- - - - -
ESEN
10.
