Kareköklü İfadeler Soruları

Tamkare Olmayan Doğal Sayıların Karekökleri / Kareköklü Bir İfadenin Farklı Gösterimi TEST-4 1. Aşağıda verilen ABCD ve KLMN dikdörtgensel bölgelerinin içine mavi ve sarı renkli kenar uzunlukları cm cinsinden doğal sayı olan dikdörtgenler çizilmiştir. 5√3 cm Y B 8√6 cm D C 7√2 cm K Buna göre mavi ve sarı dikdörtgenlerin çevreleri toplamı en çok kaç cm'dir? A) 106 B) 104 C) 102 10√3 cm D) 100 N M

N ..... :eis Yayınlan 2. 5√10 cm 30130 24130 D 6130 6√3 cm Şekil 1 A) 31-32 C) 33-34 C D BA 8- Matematik SB 6√6 cm F G 4√5 cm Şekil II B) 32-33 D) 34-35 C Yukarıda Şekil I'de gösterilen ABCD dikdörtgeninden Şe- kil Il'deki gibi GBEF dikdörtgeni kesilip atılıyor. B Buna göre, kalan çokgenin alanı santimetrekare cinsinden hangi ardışık iki tam sayı arasındadır? E eis Yayınlan 4. ol A

9. Selçuk bir fidan alıp bu fidanı dikmek için bahçesine gi- diyor. √3,61 metre Şekil-1 Şekil-2 Selçuk Şekil-1'deki gibi fidanı dikmeden önce fidanın boyu kendisinin boyundan √3,61 metre fazla olduğu- nu, fidan diktikten sonra ise kendi boyunun fidanın bo- yundan √0,81 metre fazla olduğunu görüyor. 130 Buna göre, Selçuk'un fidanı dikmek için açtığı çukur kaç metredir? A) 2,6 √0,81 metre B) 2,8 C) 3,2 D) 3,4

KAREKÖKLÜ İFADELER 11. a, b, c birer doğal sayı olmak üzere a√c = √a²c, avc+b√c = (a+b)√c, a√c-b√c = (a-b) √c dir. Tavan A B A) 2 ile 3 C) 4 ile 5 71 Yer Yukarıda verilen şekildeki gibi sabit tutulan, ayrit uzun- lukları 1 m olan, küp şeklindeki A ve B cisimlerinin ağırlıkları birbirinden farklıdır. A cismi, B cisminden ağır olup her ikisinin de yere olan uzaklıkları eşit ve √8 m'dir. B cisminin tavana olan uzaklığı √50 m'dir. Düzenek serbest bırakılıp durduğu anda, cisimler bu- lundukları tarafta kalmaktadır. Buna göre B cisminin tavana olan uzaklığı, hangi iki tam sayı arasında olur? B) 3 ile 4 D) 5 ile 6

7. Aşağıda ABMN, BCKL ve CDEF karelerinin alanları sırasıyla 289, 169 ve 100 santimetrekareull. coniesis con el ayudanige N A A, B, C ve D doğrusaldır. Buna göre, 289 cm² M L B) I-II-III B 169 cm² K F C E 100 cm² mille mondator anthelazem liebriesm D C) II - I - III 188 I. √1601 cm II.1590 cm III. √1603 cm sayılarının AD uzunluğuna en yakın olandan en uzak olana doğru sıralanışı aşağıdakilerden han- gisidir? A) I - III - II Barn Sublerenon D) III - II - 1

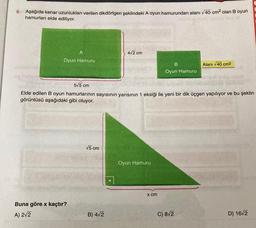
9. Aşağıda kenar uzunlukları verilen dikdörtgen şeklindeki A oyun hamurundan alanı √40 cm² olan B oyun hamurları elde ediliyor. A Oyun Hamuru Buna göre x kaçtır? A) 2√2 √5 cm 4√2 cm 5√5 cm Elde edilen B oyun hamurlarının sayısının yarısının 1 eksiği ile yeni bir dik üçgen yapılıyor ve bu şeklin görüntüsü aşağıdaki gibi oluyor. B) 4√2 Oyun Hamuru B Oyun Hamuru x cm Alanı √40 cm² C) 8√2 D) 16/2

latematik KAREKÖKLÜ SAYILAR Tam Kare Sayılar Mini Test e bir una- zunlu- uzun- D) 16 okulistik 5. Kenar uzunlukları metre cinsinden doğal sayı olan kare şeklinde iki çalışma odasından ve ke- nar uzunlukları 9 m ve 8 m olan dikdörtgen şek- linde salondan oluşan bir ofiste; çalışma oda- lanından birinin alanı salonun alanından büyük, diğerinin alanı ise salonun alanından küçüktür. Buna göre çalışma odalarının alanları arasın- daki fark en az kaç metrekaredir? 6. A) 15 B) 17 C) 19 A = √169 + √225-√289 B = √961 + √256-√121 D) 21

Kareköklü Sayılar 3. Dalga 1296√2 Kilometre Sahil S Yukarıda gösterilen tsunami dalgasının ortalama hızı saniyede 30√/72 metre olup sahile olan uzaklığı 1296√/2 kilometredir. Buna göre, sabit hızla sahile doğru ilerleyen bu dalganın sahile ulaşma süresi kaç dakikadır? A) 60 B) 90 C) 120 D) 150

5 Re 27 √20 cm Uzunluğu √180 cm olan bir tel √20 cm uzunluğunda parçalara ayrıldığında kaç parça elde edilir? A) 12 B) 9 C) 6 Çözüm √180 cm Çözüm D) 3 3 28 2 √800 kilometrelik bir yolun yarısını dakikada √8 kilometac diğer yarısını dakikada √50 kilometre hızla giden bir ar B bu yolun tamamını kaç dakikada gider? ca A) 4 B) 5 C) 6 D) 7 Sc te A

Çıkarma İşlemi =39 Daha mde is =15√2 ==15√2 -3√2 3√2 √2 7. Yukarıda verilen dikdörtgen karton, 4 eş parçaya ayrıldık- tan sonra aşağıdaki gibi ikişer ikişer üst üste konuluyor. √192 cm √108 cm Şekil-1 Şekil-2 Kartonların yükseklikleri Şekil - 1 ve Şekil - 2'deki gibi olduğuna göre başlangıçtaki dikdörtgenin bir yüzü- nün alanı kaç cm²'dir? A) 240 B) 210 C) 180 27 D) 150 -1

TEST-2 8. Aşağıda birer kenarları çakışık olan kare ve dikdört- gen kartonun birer yüzlerinin alanları sırayla 243 cm² ve 54 cm² dir. ma İşlemi 243 cm² 54 cm² Bu kartonlar kenarları çakışacak biçimde Şekil - 1'deki konuma getiriliyor. - Şekil - 1 Buna göre Şekil 1'deki kartonlardan oluşmuş yeni şeklin çevre uzunluğu kaç cm'dir? A) 48√3 B) 50√3 C) 54√3 D) 60√3

K K noktasında bulunan bir çekirge her defasında sağa veya sola √3 metre zıplayarak ilerliyor. Toplam 5 kez zıplayan bu çekirge K noktasından x metre uzaklaşıyor. Buna göre x aşağıdakilerden hangisi olamaz? A) 1<x<5 C) 6<x<9 B) 3 <x< 6 D) 9 <x< 10

13. 0 Karekök Ölçer Matematik proje ödevi için kareköklü ifade ile gösterilen uzunlukları ölçecek cetvel tasarlayan Burcu, cetvalin adını "karekök ölçer olarak isimlendiriyor. 8) Büyüteç ile iki ardışık çizgi arası √2 br olduğuna göre, A noktasının değerinin B noktasının değerine ora- ni kaçtır? D) ¹2 A) 2/2 37 √2 br C) 22

√30 √45 1. Kutu √27 √8 √48 √270 √128 2. Kutu 80 Burcu bir bilgisayar oyunu oynamaktadır. Oyunu oynarken 1. ve 2. kutuda bulunan kareköklü ifadelerden birer tane seçer ve seçmiş olduğu bu iki sayıyı çarpar. Burcu sayıları seçip çarptığında sonucu bir doğal sayı olarak bulmaktadır. Buna göre Burcu'nun bulduğu sonucun alabileceği en büyük değer ile en küçük değer arasındaki fark kaçtır? A) 58 B) 56 C) 54 D) 52 706

ç) Bir bakkal √192 kg'lık şekeri √3 kg'lık poşetlere ko- yup poşetlerin yarısını tanesi 5 TL'den, diğer yarı- sını ise tanesi 6 TL'den satıyor. Bakkalın şekerin tamamının satışından kaç TL gelir elde edeceğini bulunuz. ola

3. Yukarıda özdeş karelerden oluşan şekil verilmiştir. Her bir karenin alanı 8 cm² olduğuna göre şeklin çevresi kaç cm'dir? A) 36√2 B) 24√/2 C) 12√2 D) 8√2 /Benim Hocam 6. Aralar sıyla lerdir. 7. Buna metr A) √