Parçalı ve Mutlak Değer Fonksiyonun İntegralleri Soruları

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun İntegralleriden aldığı siparişi tamam-
det gömlek olacak şekil-
lamıştır. Siparist
tuların
Jygulama
5. "Her dersin ayrı bir güzelliği vardı sınıfta. Öğretmenleri-
miz birbirinden donanımlı kişilerdi, Dersin bir yerinde birden
bambaşka bir konudan konuşmaya başlardık Bilmezdik o
sohbetlerin de dersle alakalı olduğunu. Yıllar sonra şimdi dü-
şünüyorum da o sınıfta kişiliğime kattıklarım ne mükemmel
şeylermiş.
A) 2
18. n
B) 3
Yukarıdaki metinde haber kipiyle çekimlenmiş kaç tane
fiil vardır?
A) Anlatmazmışız
B) Anlatsaydınız
C) Anlatın
D) Anlatıyordu
MODUL
C) 4
D) 5
15
E) 6
6. "anlat-" fiilinin istek kipi 2. Çoğul kişiye göre çekimi aşa-
ğıdakilerden hangisidir?
Lise Matematik
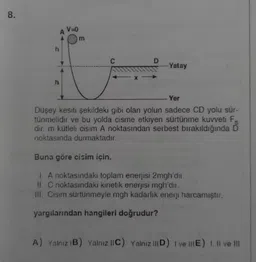
Parçalı ve Mutlak Değer Fonksiyonun İntegralleri8.
h
h
V=0
m
C
CAPEL
AP
X
D
-Yatay
Yer
Düşey kesiti şekildeki gibi olan yolun sadece CD yolu sür-
tünmelidir ve bu yolda cisme etkiyen sürtünme kuvveti F
dir. m kütleli cisim A noktasından serbest bırakıldığında D
noktasında durmaktadır.
Buna göre cisim için.
I. A noktasındaki toplam enerjisi 2mgh'dir.
II. C noktasındaki kinetik enerjisi mgh'dir.
III. Cisim sürtünmeyle mgh kadarlık enerji harcamıştır.
yargılarından hangileri doğrudur?
A) Yalnız IB) Yalnız IIC) Yalnız IIID) I ve IIIE) I, II ve III

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun İntegralleri17
75
6. Bir ülkede COVID-19 salgınından korunmak için Eylül
ayı boyunca aşılama yapılacaktır. Ülkede aşı yapılan
kişi sayısı eylül ayının x. gününde
f(x) = (x² − 3x·sina + √7cosa). 10³.
fonksiyonu ile hesaplanmaktadır.
İlk gün aşı olan kişi sayısı 5000 olduğuna göre tan(a)
değeri kaçtır?
A) -
√7
3
D) - 3√7
7
3
7
B)-
E)--7-7
C) 3√T
7
3=18
3=9
2*2=4.

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun İntegralleri30. Dik koordinat düzleminde y = k doğrusu ile y = f(x) fonk-
siyonunun grafiği aşağıda verilmiştir.
Ay
3
t ki
k
-
2
f(2x) dx = 16
41-M
olduğuna göre, k kaçtır?
A) 3 B)4
C) 5
Şekildeki kırmızı bölgenin alanı mavi bölgenin alanın-
dan 4 birimkare fazladır.
2x=4
6
flu) du
- y = k
D
D) 6
-X
2dx=du.
E) 7
16
32

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun İntegralleri22231323
22. Aşağıda, gerçel saytlar kümesinde sürekli bir f
fonksiyonunun türevinin grafiği verilmiştir.
f(2)=0
F(2) = x+c
(0)=2+C
F'(-2)=2
F(-2) = −4+E
f(2) + f(-2) =
-4
-2+2c=_
A) 2
-20
f(0) + f"(2)
toplamının değeri kaçtır?
B) 3
^y
4
olduğuna göre,
4 (6)= (
C) 5
2
D) 6
X
E) 8
24.
1
