Parçalı ve Mutlak Değer Fonksiyonun Türevi Soruları

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi4.
165
x ve y pozitif tam sayılar olmak üzere,
1230
9
x →y
10 1516
x sayısından y
sayısına kadar olan
sayıların çarpımı
x sayısından y
sayısına kadar olan
sayıların toplamı
şeklinde tanımlanmıştır.
A) 2
x sayısı ile y sayısı-
nın çarpımı
A = -
10-16
B) 3
9-19 +
x ve y çift ise
C) 4
x ve y tek ise
olduğuna göre, A sayısının kaç tane asal böleni
vardır?
x ve y'den biri
tek diğeri çift
ise
2-7
D) 5
E) 6

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevif(x) =
[x².sin, x*0
10
O
fonksiyonu veriliyor.
Buna göre, aşağıdakilerden hangisi ya da
hangileri doğrudur?
1. f, 0 noktasında türevlenebilir.
II. f' türev fonksiyonu 0 noktasında süreklidir.
III. f, 0 noktasında türevlenebilirdir.
A) Yalnız I
C) Yalnız Ill
E) II ve III
B) Yalnız II
D) I ve II

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi21. Gerçel sayılarda tanımlı bir f fonksiyonu,
x², x < 0
x³, x≥0
f(x)
biçiminde tanımlanıyor.
Buna göre, f fonksiyonu ile ilgili verilen
I. Gerçel sayılar kümesinde süreklidir.
II. Gerçel sayılar kümesinde türevlidir.
III. f'(0+)=0'dır.
ifadelerinden hangileri doğrudur?
A) Yalnız I
B) I ve II
D) II ve III
E) I, II ve III
C) I ve III

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi- SÜREKLİLİK - TÜREV
7. f: R-R,
f(x) =
[0, x < 0
1x³, x ≥0 3x
fonksiyonu veriliyor.
Buna göre, x = 0 noktasında
I. süreklidir.
H.ftürevlidir.
III. türevlidir.
ifadelerinden hangileri doğrudur?
B) I ve II
A) Yalnız I
D) II ve III
EXI, II ve III
Deneme
9.
Denem
C) IVE

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun TüreviFlo
C) 4
8. a, b ve c sıfırdan ve birbirinden farklı doğal sayılardır.
f(x) = |(2x − 3)ª. (x + 5)b. (3x − 4)c|
fonksiyonu tüm gerçek sayılarda türevli olduğuna göre,
a + b + c en az kaçtır?
AXO
A) 7
B) 8
D) 10
246
O
C) 9
ERT HOCA
24
E) 11
11.
f(x) = ³√√x -
X-
fonksiyonun
lamı kaçtır?
A) 4
12. f(x) = lax
fonksiy
göre,

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi7.) f(x) ve g'(x) sırasıyla f(x) ve g(x) fonksiyonlarının türevi
olmak üzere,
fonksiyonları veriliyor.
Buna göre,
A)
B)
g(x)=x²-x-2
D)
f(3) - g'(1)
f(0)-g'(4)
III. f(4)-g'(-2)
IV. f(−2) ·g' (2)
V. f'(5)-g(1)
ifadelerinden sonucu negatif olanlara (✓), pozitif
olanlara (x) sembolü kullanılarak yapılan aşağıdaki
değerlendirmelerden hangisi doğrudur?
x²-3x, x≤1
x>1
1
X
X
✓
X
||
|||
X
X
IV
06
X
V
X

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi3. 1. f(x) = (x-4)· |×-4
II. g(x) = |x² - 2x -81
III. h(x)=√x-4
| (x-4)(x+2)/(x^). 1x+
an
din
Yukarıda verilen fonksiyonlardan hangilerinin x = 4
apk
noktasında türevi yoktur?
A) Yalnız I
yok
200
D) II ve III
B) Yalnız III
UA
C) I ve II
E) I, II ve III
C

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevig fonksiyonu gerçel sayılarda tanımlı ve sürekli bir fonksi-
yondur.
Aşağıdaki tabloda gösterilen fonksiyonların x = 0 noktasın-
daki türevlerinden bahsedilmiştir.
x = 0
y = g(x)
Türevi yok
Buna göre, y = g(x) fonksiyonu
gisi olabilir?
A) g(x) = x
D) g(x) = |x|
0
y = g²(x)
Türevi var
9(x)
B) g(x)
1
X
y = g³(x)
Türevi var
aşağıdakilerden han-
E) g(x) =
=
C) g(x) =
1
|x|
Lise Matematik
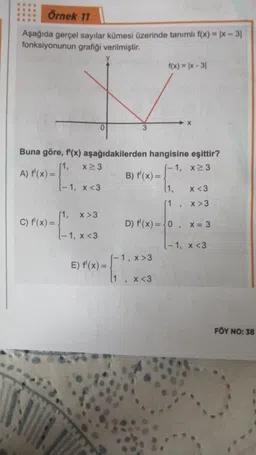
Parçalı ve Mutlak Değer Fonksiyonun TüreviÖrnek 11
Aşağıda gerçel sayılar kümesi üzerinde tanımlı f(x) = |x - 3|
fonksiyonunun grafiği verilmiştir.
C) f'(x) =
Buna göre, f'(x) aşağıdakilerden hangisine eşittir?
x ≥ 3
(-1,
x23
A) f'(x) =
-1, x <3
(1, x > 3
-1, x <3
3
E) f'(x) =
B) f'(x) =
f(x) = |x - 3|
[-1, x>3
(1, x <3
(1,
(1
1
D) f'(x)=0, x= 3
x <3
X > 3
-1, x <3
FÖY NO: 38

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun TüreviÖSYM TARZI ÇÖZÜMLÜ ÖRNEKLER
ÖRNEK - 1
Gerçel sayılar kümesi üzerinde tanımlı f fonksiyo-
nu
2
f(x) = |(x-2)³1
olduğuna göre f'(2) kaçtır?
ÖRNEK - 2
GO
Gerçel sayılar kümesi üzerinde tanımlı
f(x) = (x3 - 4x) - (x + 2)³1
unun türevsiz olduğu noktaların aps
![MH
f
8
S
TEMEL TANIM TESTI
2
DÖrnek - 179
7
m
[f(x).x]*
2
DÖrnek - 180
24
Yukarıda grafiği verilen y = f(x) fonksiyonu için,
8
8
f(x) dx = 24 ve
olduğuna göre, m kaçtır?
f(x).1 + x. f(x). = 46
¿
2
8
y = f(x)
x-f'(x) dx = 22
f(8).8-f(2)·2=46
56-2₁ f(2)=46
5=m](https://media.kunduz.com/media/question/seo/raw/20230203161821657110-5201948.jpg?w=256)
Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun TüreviMH
f
8
S
TEMEL TANIM TESTI
2
DÖrnek - 179
7
m
[f(x).x]*
2
DÖrnek - 180
24
Yukarıda grafiği verilen y = f(x) fonksiyonu için,
8
8
f(x) dx = 24 ve
olduğuna göre, m kaçtır?
f(x).1 + x. f(x). = 46
¿
2
8
y = f(x)
x-f'(x) dx = 22
f(8).8-f(2)·2=46
56-2₁ f(2)=46
5=m

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevifonksiyonunun türevinin olmadığı x değerlerinin top-
lamı kaçtır?
A)-4-
51211k
olustura
B)-3
*ler de
treuse
scentilip bowmer.
. Gerçel sayılarda tanımlı,
[ax - 3 x≥1
- A) -3
f(x) = x+bu
2
X2+2
x. (x-3). (x+3
B)
U14
λ
V2
5
2
3
3
Orijinal Yayınları
U.v!
X<1
2-x-b
şeklinde tanımlanan f fonksiyonu her x gerçel sayısı 4
için türevli olduğuna göre, a b çarpımı kaçtır?
C)
ON
8
3
D)
X+1
e
E) 3
4
3
L 2
4
x=3
Uv-u.v¹
}₁
a = 1 (2) - (x+b)
U
"A
ORIJINAL
2-(x+6)
E) -2
(x+b). 1-

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi9. Bir elektrik dağıtım şirketi abonelerinden 100 W'a kadar kul-
landıkları elektrik için sabit 25 TL, 100 W'tan sonraki her
1 Wiçin 0,15 TL almaktadır. Bu fiyatlara tüm vergi ve gider-
ler dahildir.
Buna göre, bu şirkete bağlı bir abone 700 W elektrik
kullandığında bu kullanımdan dolayı elektrik faturası
kaç TL gelir?
A) 115
B) 130
C) 135
D) 140
E) 145

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi26)
fonksiyonu her x gerçek sayısı için türevli olduğuna
liştır? göre, m nin alabileceği tam sayıların toplamı kaçtır?
= 2
x ²1
a
27)
1 = You
1. f(x)=√x-2
2
100)=2x² + (m - 3)x+ --
f(x)
+(m-3)x+
A) Yalnızl
B) Yalnız II
II. g(x) = x - 21
III. h(x) = x² - 4x +41
fonksiyonlarından hangileri x = 2 noktasında türevlidir?
D) I ve III
29)
E) II ve III
-4
Yukarıda f(x)
Buna göre,
sizdir?
A) 3
C) Yalnız II
30)201
Baş kat
polino
P(
old
A) 3
P

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevix)=√xa fonksiyonu veri-
el sayısı kaça eşittir?
44 D) 2
E) 6
dobijon
Haso?
11. Tanımlı olduğu aralıkta
f(x) = ³√x
fonksiyonu veriliyor.
d²f(x)
dx²
A)
-
2
9
ifadesinin x = 1 için değeri kaçtır?
B) 1
3
D) - D) //
-1/3

Lise Matematik
Parçalı ve Mutlak Değer Fonksiyonun Türevi4. Zafer çevresi 920 birim olan Şekil 1'deki koşu pistinde
3 tam tur, Erkan ise çevresi 339 birim olan Şekil 2'deki koşu
pistinde 27 tam tur atmıştır.
Şekil 1
Şekil 2
Buna göre, Erkan'ın koştuğu mesafe, Zafer'in koştuğu
mesafenin kaç katına eşittir?
1
